基于风力发电机组传动链扭转频率的研究与应用

兰杰，林淑，宋聚众

（东方电气风电有限公司，四川德阳，618000）



基于风力发电机组传动链扭转频率的研究与应用

兰杰，林淑，宋聚众

（东方电气风电有限公司，四川德阳，618000）

摘要：为了准确地分析风力发电机组传动链扭转频率，考虑风力机与发电机之间传动轴扭转柔性的作用，通过等效的两质量块模型，建立了风力发电机组传动链数学模型，结合模态分析法，计算出了该模型的2个模态频率，并通过实际物理意义，获得了表征传动链扭转频率的计算公式。并以FD70B风力发电机组设计为例，将所得计算公式应用到实际测量数据中，分析出实际传动链扭转频率，并依据传动链扭转频率计算公式来指导模型参数校正，更好地为风力发电机的设计和应用提供理论依据和技术支撑。

关键词：风力发电机组，传动链，扭转频率，参数校正

0　引言

随着风能利用率要求的不断提高，对风力发电机组的结构、控制方式也提出了新的要求［1］。风力发电其实质是将风能转换成机械能再进一步转换成电能的过程。由风轮到发电机构成了整个风机的传动链，因其结构复杂、精度要求高，所以动态性能的好坏也将直接影响整个系统的性能和传动效率，研究传动链频率问题对将来设计更大的机型具有重要意义和工程价值。风力发电机组的传动链在传动过程中会产生较大振动、噪声和动载荷，对整机的稳定性、可靠性和寿命有较大影响，因而对传动链的动态特性提出了更高的要求［2］。随着风力发电机风轮直径不断增大，传动链的柔性不断增加，传动链扭转频率对系统控制的影响也越来越大，开展传动系统的分析具有重大工程实用价值［3］。然而，对现有文献分析发现，仅从发电机本体的数学模型、控制策略进行研究的居多［4-5］，对风机传动系统动态特性的研究分析却很少，当前主要有2种：（1）基于实验数据辨识建立模型的方法；（2）基于机理建模的方法。文献［6］使用前者建立传动系统的动态模型，因风力发电机的实验数据比较难获取及应用范围比较窄而很少应用。文献［7］视主轴为柔性轴，构造了柔性轴动力学模型。此方法可用于中小型风力机传动系统，对兆瓦级风力机而言，其会造成很大的误差。即便如此，针对传动链，如何通过实际测量数据，修正理论模型，并优化控制也亟待深入研究。鉴于此，本文采用等效集中质量模型方法，对风机传动链的频率进行了研究，建立起了传动链的数学模型，获得了表征传动链扭转频率的计算公式，并以FD70B风力发电机组为例，将其应用到实际测量数据中，分析出实际传动链扭转频率，依据推导的传动链扭转频率计算公式来指导模型参数校正，更好地为现场风机控制器参数调整设计提供依据。

1　风力机传动链模型分析

风力发电机的传动链主要由风轮、低速轴、齿轮箱、高速轴、发电机等构成［8］，如图1所示。

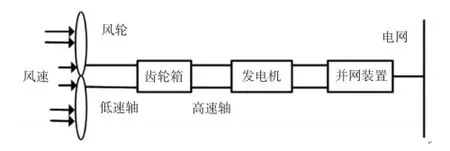
图1　风力发电机组传动链结构示意图

考虑到风机轮毂和发电机之间低速轴传动链的柔性，将风力机叶片和轮毂等效成1个质量块，齿轮箱和发电机转子等效成1个质量块，等效为2个质量块的风力机传动链模型如图2所示。

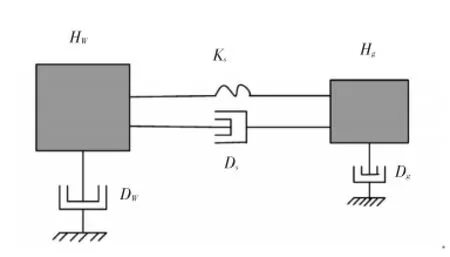
图2风力机传动链等效模型示意图

图2中：HW为风轮转动惯量；DW为风轮阻尼系数；Hg为折算到低速轴侧发电机+齿轮箱的转动惯量；Dg为折算到低速轴侧发电机+齿轮箱的阻尼系数；Ks为传动轴的刚度系数；Ds为传动轴的阻尼系数。

由此可列出风力机传动链等效2个质量块的数学模型如下：

式中：TA为风轮上气动力矩；Tg为折算到低速轴侧电机电磁力矩；Ts为低速轴扭矩；θW为风轮转角；θg为风力机相对于发电机转子的角位移。

将式（3）带入式（1）、（2）中，并改写成矩阵形式如下：

令T=0，并且不考虑阻尼矩阵，就得到了无阻尼自由振动方程，如式（5）所示。

根据式（5）推导可以得到2个质量块模型的2个模态频率分别为：

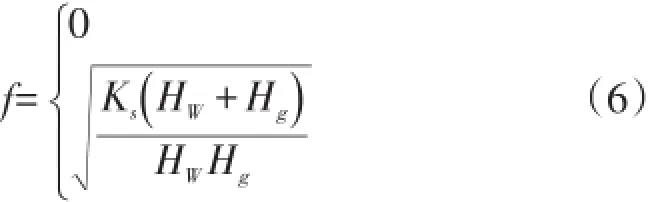
式（6）中有1个模态频率为0，表明存在1个做刚体自由转动的模态，另1个模态频率即为传动链频率。

2　应用

在风力发电机设计控制器算法过程中，通过上述分析，可知传动链存在阻尼较低的扭振固有频率，如果不加以抑制，风力发电机组的齿轮箱在传动过程中会产生较大振动、噪声和动载荷，会对齿轮箱造成很大的疲劳损伤，因此需要对传动链设计专门阻尼控制器，增加传动链阻尼，从而降低齿轮箱疲劳载荷，阻尼控制器结构如图3所示。

图3　传动链阻尼控制器结构框图

若实际传动链频率与理论有较大偏差，设计的阻尼控制器就达不到预期的效果。

如果与设计模型传动链频率相差较大，就需要调整模型参数，使模型与实际测量值相匹配。通过式（6）很容易知道，可以调整的参数有3个，分别是：风轮转动惯量HW，折算到低速轴侧发电机+齿轮箱的转动惯量Hg，传动轴的刚度系数Ks。

将式（6）进行整理变形，得到式（7）。

并定义等效总转动惯量见式（8）。

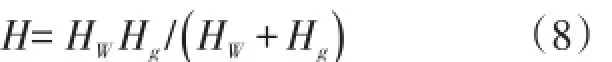
而一般情况下风轮转动惯量HW和折算后高速轴转动惯量Hg比较精确，因此当模型扭转频率与实测扭转频率存在较大误差时，可通过调整Ks来校正设计模型。

以FD70B机型为例，初步理论设计模型传动链频率为2.372 7 Hz，而通过现场实测数据，并进行功率谱分析，如图4所示。

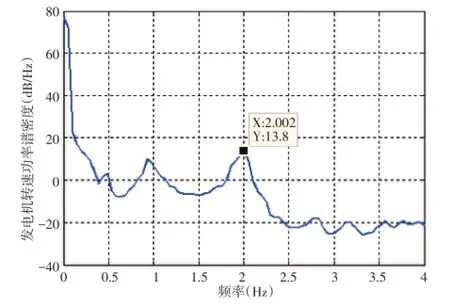
图4　实测转速信号功率谱

从图4得知，传动链扭振频率为2.002 Hz，与初步设计模型有一定偏差，通过修改低速轴刚度参数，得到新的系统模型，并重新设计阻尼控制器。修正系统模型后进行仿真计算对比。

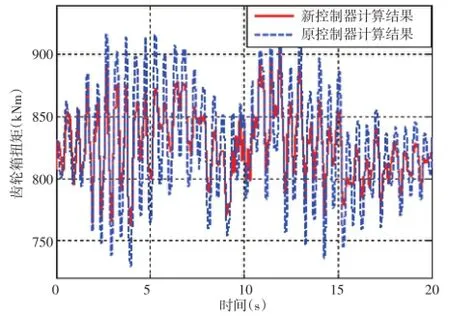
图5　齿轮箱扭矩对比

图6　齿轮箱扭矩功率谱对比

图7　发电机转速对比

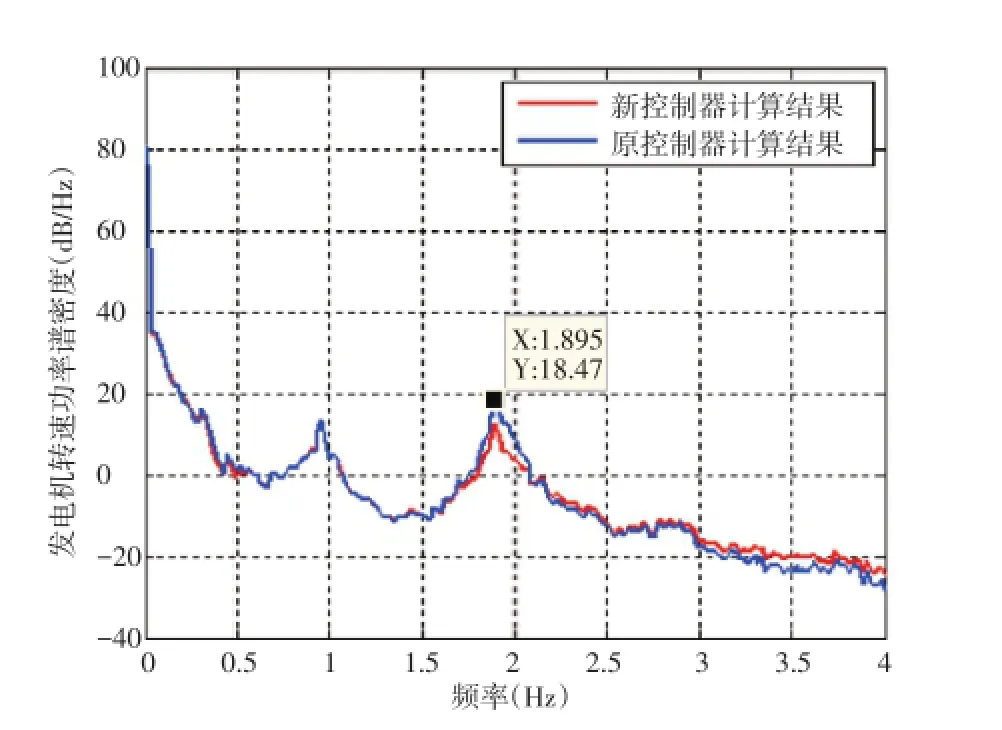
图8　发电机转速功率谱对比

从图5～图8可得，若继续采用原控制器进行控制，将增大齿轮箱疲劳载荷，降低使用寿命，重新调整阻尼控制器参数，通过选取风况近似的实际运行数据对比，如图9所示。

图9　实测运行风速对比

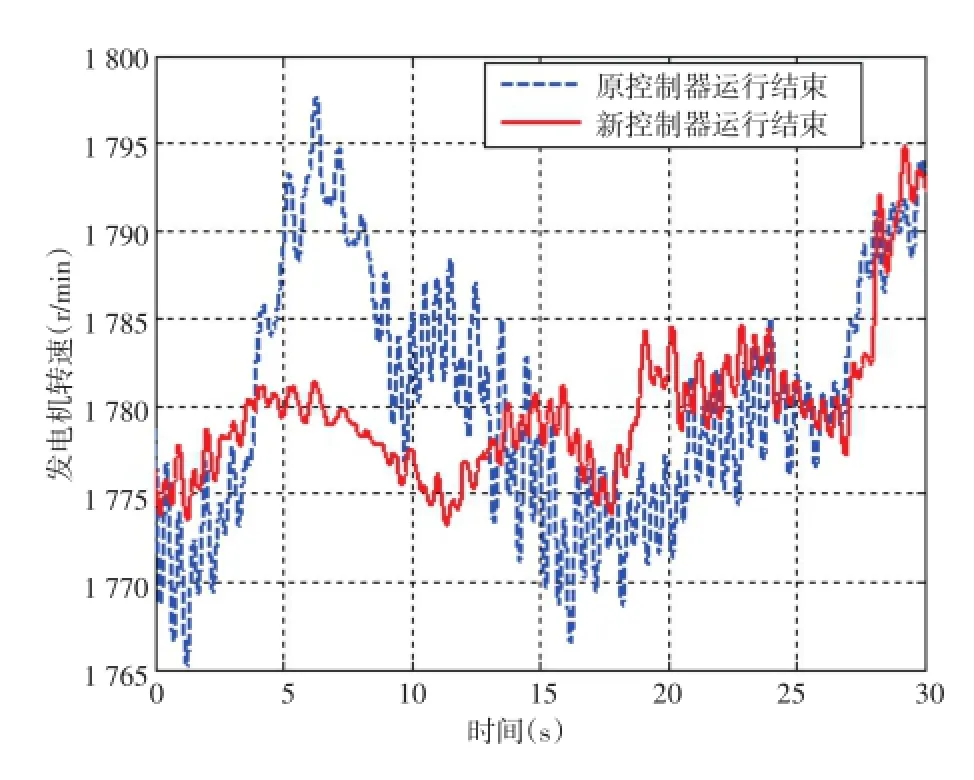
图10　实际运行发电机转速对比

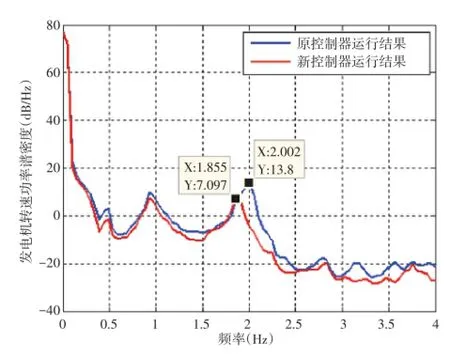
图11　实际运行发电机转速功率谱对比

从图10可知，修改模型参数后重新调整控制器，发电机转速波动降低，进一步分析发电机转速频谱。从图11可知，修改模型参数后重新调整控制器，发电机转速测量信号在传动链频率附近，只有1.855 Hz的风轮6P频率，而没有明显的传动链扭振频率信号，可降低齿轮箱振动，延长风力发电机的寿命。

3　结语

风机传动链因其结构复杂、精度要求高，故其动态性能的好坏直接影响整个系统的性能和传动效率。本文通过分析，获得了表征传动链扭转频率的计算公式，通过实际测量数据，分析出实际传动链扭转频率，依据推导的传动链扭转频率计算公式来指导模型参数校正，并通过现场实际运行来验证了该方法的有效性，为风电机组的设计和应用提供理论依据和技术支撑。

参考文献

［1］Chen Z.Issues of connecting wind farms into power systems ［C］.2005 IEEE/PES Transmission and Distribution Conference&Exhibition:Asia and Pacific，Dalian，China，2005.

［2］Hansen M，Hansen A，Fuglsang P，et al.Control design for a pitch-regulated，variable speed wind turbine［R］.Denmark: Riso National Laboratory，2005.

［3］Seman S，IOV F，Niiranen J，et al.Advanced modeling of doubly fed induction generator wind turbine under network disturbance［C］//Proc 5th Int Workshop Large-scale Integration Wind Power Transmission Networks Offshore Wind Farms，April 7-8，2005，Glasgow，UK.2005:305-314.

［4］杨之俊，吴红斌，丁明，等.故障时双馈风力发电系统的控制策略研究［J］.电力系统保护与控制，2010，38（1）:14-18，36.

［5］包能胜，朱瑞丹，倪维斗.大型风电场电网三相短路故障暂态分析［J］.太阳能学报，2008，29（9）:1161-1166.

［6］Leithead W E，Rogers M CM.Design of a controller for a test-rig for a variable speed wind turbine control applications ［C］.Proceedings of the Third IEEE Conference on，1994.

［7］接勐，崔新维，谢建华，等.机械系统状态空间法在风力发电机主轴系统上的应用［J］.新疆农业大学学报，2006，29（3）: 98-100.

［8］李辉，叶仁杰，高强，等.传动链模型参数对双馈风电机组暂态性能影响［J］.电机与控制学报，2010，14（3）:24-30.

［9］Bossanyi E A.GH bladed user manual［R］.Bristol:Garrand Hassan and Partners Limited，2009.

基金编号：四川省科技支撑计划项目资助项目（2014 G20084）。

Study and Application on Drive Train Torsional Frequency Based on Wind Turbine

Lan Jie，Lin Shu，Song Juzhong
（Dongfang Electric Wind Power Co.，Ltd.，Deyang Sichuan，618000）

Abstract:In order to accurately analyze wind turbine drive train torsional frequency，considering the factor of the drive train shaft ten⁃sional flexibility between a wind turbine and a generator，a wind turbine drive train mathematical model was established by using two equivalent lump mass models in this paper.Then combining with the modal analysis method to calculate two modal frequencies of the model，the calculation formula of drive train torsional frequency was received by the actual physical meaning.Taking FD70B wind tur⁃bine as an example，it was easy to apply the formula to the actual measurement data and analyze the actual drive train torsional fre⁃quency，then guide the model parameter calibration based on the drive train torsional frequency calculation formula.It was better to provide theoretical basis and technical support for the design and application of wind turbine.

Key words:wind turbine，drive train，torsional frequency，parameter calibration

中图分类号：TK 263

文献标识码：A

文章编号：1674-9987（2016）02-0059-05

DOI:10.13808/j.cnki.issn1674-9987.2016.02.014

作者简介：兰杰（1985-），男，工学硕士，工程师，2011年毕业于四川大学控制理论与控制工程专业，现从事风电控制设计工作。