兆瓦级风电机组传动链动力学建模及仿真方法研究
2016-07-23刘桦邓良阳小林
刘桦,邓良,阳小林
(东方电气风电有限公司,四川德阳,618000)
兆瓦级风电机组传动链动力学建模及仿真方法研究
刘桦,邓良,阳小林
(东方电气风电有限公司,四川德阳,618000)
摘要:以某兆瓦级风电机组为例,根据德国劳埃德2010版风机认证规范要求,绘制了机组传动链动力学拓扑图,建立了包含多自由度刚柔部件的机组传动链模型。根据传动链模型,进行了频域分析,得到了机组传动链模态频率,绘制了二维Campbell图,找到了传动链潜在共振点,并通过时域扫频分析,验证了共振点的分析结果。与Bladed结果进行比较,验证了仿真分析结果的正确性。
关键词:兆瓦级风电机组,传动链,动力学仿真
1 前言
风力发电机组是风能领域的一种旋转能源机械,其动力学特性主要由机组的传动链特性决定。掌握风电机组传动链运动特性,是进行机组振动分析及控制设计等工作的重要基础;同时,通过对运行工况的时域分析,可以考察机组运动和部件受力情况,对了解机组运动及部件设计有帮助,因此传动链动力学分析是风电机组设计中一项重要工作。
对于小型风电机组,其传动链动力学特性主要受传动链部件的质量、转动惯量、刚度和阻尼等因素影响,而随着近十年来风电机组单机功率和部件尺寸的不断增大,部件的柔性及传动链支承特性对传动链动力学特性的影响也逐渐明显,因此在兆瓦级风电机组传动链模型仿真分析中,必须予以考虑。近年来,国内外对兆瓦级风电机组传动链建模做了较多研究。
荷兰能源研究中心(ECN)采用通用多体动力学软件对风电机组变桨系统、传动链系统进行了仿真建模分析[1]。模型包含柔性叶片和塔架、传动链、齿轮箱、齿轮箱支承以及外部气动力输入等单元,模拟了机组运行转速、功率、变桨角、叶根载荷、部件变形以及其他机组部件运行动态数据,通过与测试数据对比,验证了模型的正确性,相较于单独的部件分析,由于考虑了部件之间的相互影响,其结果更具有可靠性。
德国Technical University of Dresden的Berthold Schlecht等采用多体动力学软件对风电机组传动链模型进行了时域和频域仿真分析,除了模拟机组运行时的运动及载荷时序数据,同时也计算了机组传动链的频率结果,并分析了各个部件模态之间的相互影响和模态能量分布特征,为机组振动分析和控制设计提供了参考[2]。
德国Rwth Acchen Unverstiy的Schelenz等采用风机传动链模型模拟了不同气动模型对机组动态特性的影响[3];Stuttgart University的Hauptmann等研究了采用风机传动链模型与Matlab联合仿真,进行机组控制系统设计的方法[4]。
2 风电机组传动链模型的建立
机组传动链模型的建立首先需要绘制传动链拓扑图,其次进行传动链部件建模,并确定模型力元参数,然后综合建立整个机组传动链模型。
以某双馈风电机组为例,其单机功率达到2.5 MW,风轮直径超过100 m,机组安装的大尺寸叶片、主轴以及齿轮箱等部件的柔性将显著改变机组传动链动力学特性,此外齿轮箱和电机支承的刚度和阻尼也会对机组传动链动力学特性造成明显的影响。因此必须建立符合兆瓦级风电机组传动链动力学特性的刚柔耦合传动链模型,并采用正确的分析方法进行仿真分析,才可以得到反映机组实际情况的结果。
2.1风电机组传动链拓扑图
机组传动链模型的拓扑图表示组成传动链各个部件之间的运动和受力的树型关系。绘制拓扑图,可以分析传动链部件运动和受力关系,还可以定义部件之间的自由度数目和类型,以及部件间相互作用力元类型、作用点和大小等关键建模元素。因此绘制传动链模型拓扑图是分析传动链模型部件运动关系的重要工具,也是建立总体模型的基础。
以前述双馈风电机组为例,该机组传动链属于常规两点支承布局,齿轮箱与电机通过高速轴联轴器连接,齿轮箱和电机通过弹性支承安装在机架上。根据机组传动链模型的复杂程度,绘制的拓扑图分为机组传动链拓扑图和齿轮箱拓扑图,机组传动链拓扑结构图如图1所示。
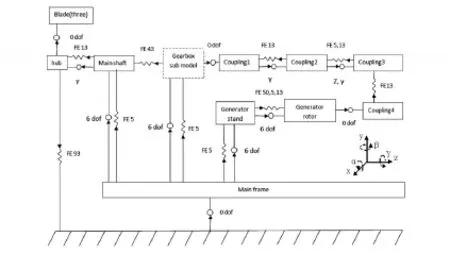
图1 机组传动链拓扑结构图
如图1所示,机组传动链模型由所有传递扭矩的部件组成,包括叶片、轮毂、主轴、主轴轴承、齿轮箱、高速轴联轴器、电机,以及齿轮箱和电机的弹性支承等。其中由于塔筒及机架对传动链动力学特性的影响可忽略不计,因此模型中略去塔筒,将机架设置为刚体,并与大地坐标系固连。
大地坐标系的z轴平行于水平面,并指向风轮下风向方向,y轴垂直向上,x轴与y轴和z轴构成右手坐标系。图中的“α”为绕x轴的旋转方向;“β”为绕y轴旋转方向;“γ”为绕z轴旋转方向。
在机组传动链拓扑图中,叶片与轮毂固接;轮毂与主轴之间有γ方向旋转自由度,通过表示轮毂扭转刚度的力元连接;主轴相对于机架具有6个自由度,通过主轴轴承刚度矩阵力元安装在机架的轴承座上,此外主轴与齿轮箱通过弹簧阻尼力元连接,表示主轴与齿轮箱之间的胀套连接;齿轮箱相对于机架也具有6个自由度,通过齿轮箱弹性支承刚度矩阵力元安装在机架上;齿轮箱与高速轴联轴器固接,高速轴联轴器采用4个由弹簧阻尼力元连接刚体表示,刚体之间具有前后方向和γ方向自由度,表示联轴器的纵向、横向和扭转运动;联轴器与发电机转子固连,发电机转子具有6个自由度,通过电机轴承刚度矩阵力元安装在发电机定子上;电机定子同样具有6个自由度,通过电机弹性支承安装在机架上,以此组成完整的机组传动链拓扑图。
在传动链拓扑图中,齿轮箱作为1个子结构表示,由于其内部具有复杂的轴系和齿轮动力学关系,因此需要单独建立齿轮箱子模型。风电机组齿轮箱包括齿轮箱箱体、低速级行星架、主轴胀套连接、低速级内齿圈、低速级行星轮、低速级太阳轮、中速级输入轴、中速级行星架、中速级内齿圈、中速级行星轮、中速级太阳轮、高速级输入轴、高速级大齿轮轴、高速级大齿轮、高速级小齿轮轴和高速级小齿轮等部件。各级行星架、高速级大齿轮和小齿轮等部件具有6个自由度,通过轴承刚度矩阵力元安装到齿轮箱箱体,各个齿轮副的啮合力由啮合力元表示。
2.2风电机组传动链部件建模
传动链模型中的部件建模根据其柔性对传动链动力学特性影响的程度分为柔性部件建模和刚性部件建模。
本文采用德国劳埃德2010版风电机组认证规范[5]的建议进行分类,如表1所示。
对于刚体部件,需要给出部件模型的质量、转动惯量和质心位置参数;对于柔性体部件,除了以上参数外,还需要对部件进行模态分析,将结果导入部件模型,完成柔性体部件建模;轴承采用支承刚度矩阵力元表示;传动链弹性支承用弹簧阻尼力元表示。
由于篇幅所限,以下以轮毂和叶片为例,简要说明刚体和柔性体部件的建立过程。

表1 传动链部件处理方式
轮毂材料为QT350,为塑性铸铁材料[6]。轮毂刚体模型参数可由测量得到或从实体模型中读出。此外需要考虑轮毂扭转刚度对传动链特性的影响,可以根据轮毂有限元模型在单位载荷下轮毂的角位移量计算得到。计算轮毂刚度的有限元模型[7]如图2所示。

图2 轮毂扭转变形结果图
机组的叶片采用复合材料制成,材料属性为各向异性,因此采用含有叶片参数的数据表给出所需部件模型数据,如表2所示。

表2 叶片建模数据表
根据表2的叶片数据,建立叶片有限元模型进行模态分析,将结果读入叶片模型中,完成叶片柔性体的建立。叶片外形如图3所示。

图3 叶片模型
单只叶片的质量为11 636 kg,叶片一阶拍动和挥舞频率分别为0.64 Hz和1.18 Hz,叶片二阶拍动和挥舞频率分别为1.81 Hz和3.60 Hz。
机组传动链模型中的齿轮箱名义速比为84.5,采用常规的两级行星轮和一级平行轮布局。建立完成的齿轮箱仿真模型如图4所示。

图4 齿轮箱模型
齿轮箱模型中,齿轮箱箱体、低速级和中速级行星架、所有齿轮轴处理为柔性体,低速级和中速级行星轮处理为刚体,轴承处理为刚度矩阵力元。
齿轮箱箱体通过齿轮箱弹性支承刚度和阻尼力元安装到刚性机架。行星架和所有齿轮轴通过轴承刚度矩阵力元安装在箱体内对应的各个轴承安装孔的中心。各个齿轮副之间的啮合力通过啮合力元模拟。
齿轮箱的柔性部件建模过程与叶片柔性体建模过程基本一致,即首先建立部件有限元模型,然后进行模态分析,最后将模态分析结果导入到部件模型中,完成柔性部件建模。
齿轮箱柔性部件模型中都设置一个铰接点,部件通过该铰接点与其他部件相连,并给定自由度。此外,在轴承、花键和齿轮中心处设置Mark⁃er点,用于连接轴承刚度矩阵力元、花键力元以及齿轮副啮合力元。
各个部件的有限元模型如图5所示。

图5 齿轮箱各部件有限元模型
在机组传动链中,高速轴联轴器是连接电机与齿轮箱高速轴的部件。传动链仿真模型中,将联轴器处理为4段由弹簧和阻尼连接的刚体组成,如图6所示。
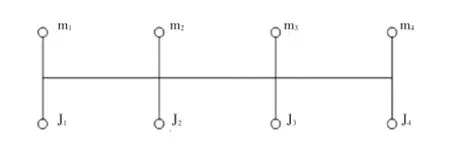
图6 高速轴联轴器参数图
其中,图中m1为第1段刚体质量,对应的m2、m3和m4为第2、3和4段刚体质量,两段刚体之间通过1个扭转弹簧连接,表示联轴器的扭转刚度。此外,为了表示联轴器轴向刚度,在联轴器第2段与第3段刚体之间设置1个平动刚度弹簧,表示联轴器轴向方向的刚度。
在传动链仿真模型中,将发电机处理为电机转子、电机定子、电机弹性支承和电机轴承组成。电机转子通过电机轴承刚度矩阵力元安装到电机定子,电机定子通过电机弹性支承刚度力元安装在刚性机架上。在模型仿真分析中,由于电机转子和定子对传动链动力学特性影响可以忽略,因此模型中将两者都简化处理为刚体。
2.3传动链模型力元的确定
在机组传动链模型中,部件之间有力元作用,如轴承刚度矩阵力元、弹簧力元、扭转力元、齿轮副啮合力元,以及外部时间激励力元等。它们的类型及参数对传动链动力学特性有很大影响,因此必须在传动链模型中确定。对于某些力元,如轴承的刚度矩阵力元,可以参考轴承在不同受力情况下,各个方向的刚度数据给定。另外一些力元由于缺乏参数值,则需要根据力学公式计算确定。如齿轮箱弹性支承和电机弹性支承力元的阻尼值,以及高速轴联轴器弹簧阻尼力元等。
对于齿轮箱弹性支承,根据力元不同平动方向的刚度和阻尼因子数据,以及齿轮箱弹性支承中心距离齿轮箱输入轴中心距离计算出力元的阻尼值。首先计算齿轮箱转动惯量,包括叶片、轮毂、主轴和齿轮箱箱体惯量,然后根据弹性支承力臂长度,计算齿轮箱等效质量,最后根据振动力学,阻尼值计算见式(1)。

式中:D为阻尼因子;K为单个弹性支承线性刚度;n为弹性支承个数。求出代表齿轮箱弹性支承的弹簧阻尼力元的阻尼值。
发电机弹性支承和高速轴联轴器的弹簧阻尼力元的计算过程类似,这里不再赘述。表3、表4分别为计算得到弹性支承力元和高速轴联轴器力元刚度和参数值。
机组传动链模型中有2个外力矩:1个是气动输入力矩;另1个是发电机反馈力矩,当两者达到平衡时,传动链模型达到稳定运动状态。

表3 齿轮箱和发电机弹性支承力元参数值

表4 高速轴联轴器的力元参数值
机组传动链模型仿真分析中,将气动输入力矩简化为作用在轮毂中心的输入力矩。该力矩通过1个施加在轮毂中心的时间激励力元表示。根据不同的分析目的,气动输入力矩分为传动链动态平衡仿真计算时的输入力矩和风轮转速扫频计算时的输入力矩。在动平衡计算中,气动输入力矩相对于时间是恒定不变的。扫频计算中,传动链模型将在气动输入力矩的驱动下,风轮转速从切入转速增加到切出转速,此时气动输入力矩分为2个分量,见式(2)。

式中Tacc为恒定力矩分量,它起到加速传动链转速的作用;Timb为风轮受风剪和塔影效应引起的不平衡力矩分量。
气动不平衡力矩分量随方位角变化情况如图7所示。
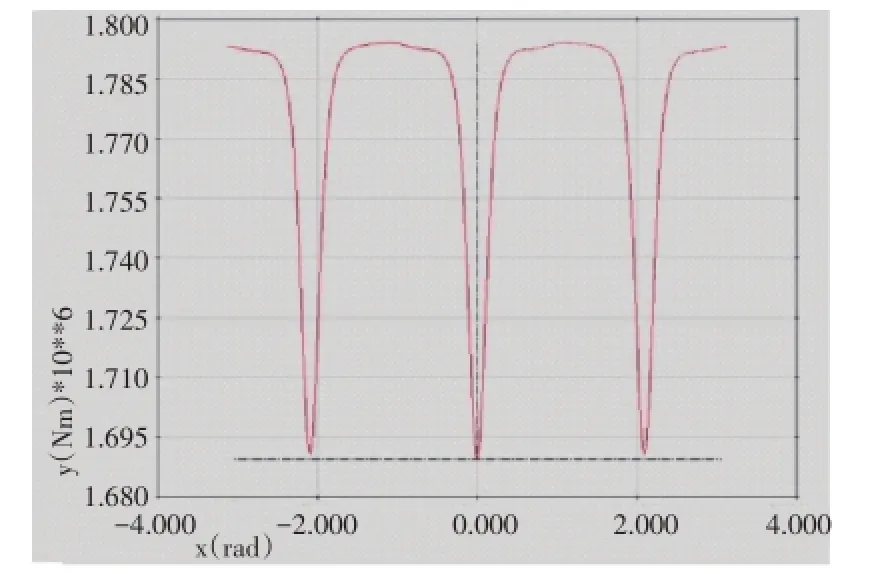
图7 气动输入力矩不平衡分量变化
发电机反馈力矩作用在发电机转子和定子之间,根据电机输入转速给定反馈力矩力元大小。发电机反馈力矩如图8所示。

图8 机组发电机转速vs力矩曲线
根据2.1节的机组传动链拓扑图,将以上建立的部件模型根据相互运动关系,用铰接和力元连接起来,形成某风电机组传动链仿真模型[8],如图9所示。

图9 机组传动链整体模型
3 机组传动链模型频域分析
根据建立的机组传动链模型,可以对传动链进行频域分析,包括传动链模态频率计算、激励频率分析、传动链Campbell图的绘制,以及潜在共振点分析等内容。
传动链模态频率的计算是在传动链模型上施加恒定气动输入力矩及电机反馈力矩,使传动链模型达到稳态运行状态。然后进行特征值分析,得到传动链模态频率及模态阻尼因子。由于传动链扭转方向频率对动态特性影响较大,因此略去其他方向结果。额定运行点的扭转模态频率结果如表5所示。

表5 模态频率计阻尼因子结果
本文计算了前22阶传动链扭转模态频率。将分析得到的模态频率与Bladed计算得到的频率结果进行比较,如表6所示。
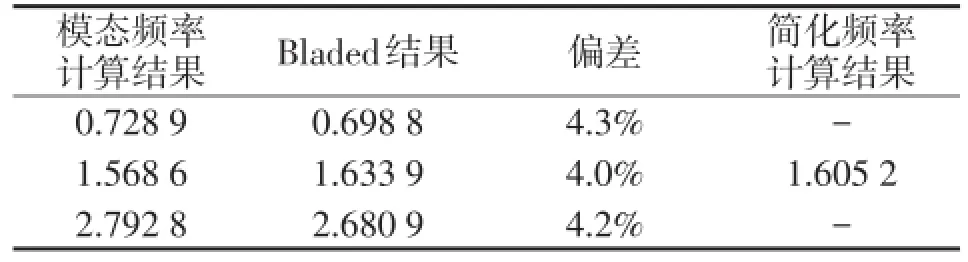
表6 模态频率结果对比
计算得到的前3阶模态频率与Bladed结果偏差在5%以内,其中1阶扭转模态频率f_N01为1.568 6 Hz,简单手算结果为1.605 2 Hz,Bladed计算结果为1.633 9 Hz,计算结果可信。
此外传动链的各阶模态频率在不同工作点处有一定变化。机组在切入、切出工作点下的传动链模态频率结果如表7所示。

表7 不同工作点下的传动链模态频率结果
传动链模态频率在不同工作点处基本完全相同,造成差异的原因是不同工作点下,风轮转速变化引起的叶片动态刚化现象造成的。

表8 机组传动链激励频率
该机组正常运行时,风轮工作转速在7.91~15.66 r/min之间,额定转速为14.23 r/min。根据机组运行数据及齿轮箱轮系参数,计算传动链激励频率如表8所示。
传动链的最高激励频率为高速级齿轮副啮合频率的3倍频:2 178 Hz。由于更高频率对机组传动链动态特性影响较小,因此在传动链频率分析中忽略不计。
根据以上计算得到的机组传动链激励频率和模态频率,可以绘制传动链二维Campbell图。其中模态频率0~5.6 Hz范围的Campbell图如图10所示。

图10传动链Campbell图
图10中纵向坐标为模态频率,横向坐标为风轮转速。水平线表示传动链各阶模态频率,斜线表示传动链激励频率,垂直线为风机额定工作点参考线。
Campbell图中,传动链模态频率与激励频率的交叉点表示机组传动链可能的共振点,但并不意味传动链就会出现共振,这需要结合交点处的部件能量分布和激励频率判断。例如第1阶模态频率与中速级输入轴2倍频有交点,其能量分布如图11所示。
如图11可见,f_N1的振动能量主要分布在高速轴联轴器,它与中速级输入轴激励频率shaft1_ 2p有交点。由于产生激励频率的部件(中速级)与模态能量集中的部件(联轴器)不在1个转速段内,较低的激励频率对较高频率部件的振动激励影响不明显,因此认为该交点不会激励传动链发生共振。相反如果产生激励频率的部件与模态能量集中的部件相同,或位于1个转速段内,那么就有可能产生共振。
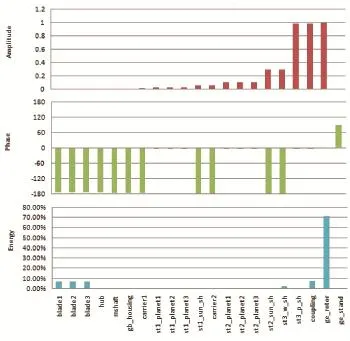
图11 f_N1的幅值、相位和能量分布情况
Bladed计算得到的一阶扭转频率的能量如表9所示。

表9 Bladed计算得到的一阶扭转频率能量表
其中,Generator rotation表示电机转子的能量百分比;Rotor in plane mode 3表示风轮第3阶能量百分比。与图11比较,主要能量分布在电机转子和风轮,两者的部件模态能量分布趋势一致。
根据以上流程,对传动链Campbell图中所有交点(共22个交点,这里略去详细分析过程)逐一进行分析,即可把所有潜在的共振点找出来。但潜在共振点也不一定表示该点会出现传动链共振,需要对潜在共振点进行时域扫频分析才能最终确定。
4 机组传动链模型时域分析
为了最终验证机组传动链共振点的个数及位置,需要在时域中对发现的潜在共振点进行扫频分析。
如2.3节所述,时域扫频分析时,需要在轮毂中心施加气动驱动力矩。
传动链模型将从切入转速加速到切出转速,如图12所示。

图12 扫频分析时轮毂转速曲线
此时,轮毂角加速度曲线如图13所示。
图13 扫频分析时轮毂角加速度曲线
在潜在共振点出现的位置,对部件加速度时序数据进行截取和频谱分析,得到共振点处的部件能量分布。如果该部件能量分布出现明显的增加或突变,就说明机组传动链在该潜在共振点处出现了共振。
例如,某潜在共振点的机组模态频率为f_N6= 18.534 5 Hz,激励频率为shaft2_3p,模态能量集中在发电机定子。可以求得,f_N6与shaft3_1p的交点处风轮转速约为13.2 r/min,对应在扫频分析中的仿真时间点为89.62 s,因此对该时间点附近的发电机定子角加速度时序数据进行频谱分析,得到的定子角加速度频谱图如图14所示。

图14 发电机定子角加速度频谱图
如图14所示,发电机定子角加速度频谱图中,在模态频率f_N6=18.534 5 Hz附近有明显峰值,但如图所示,该峰值很小,不超过1.6e-16,说明中速级齿轮轴转频的3倍频对定子振动的激励可以忽略,因此认为该潜在共振点不会引起共振。
按以上方法对所有潜在共振点进行扫频分析后,可以得到最终的传动链危险共振点出现的频率及具体部件。
对于某兆瓦级风电机组传动链,通过频域及时域动力学分析后,结果显示该传动链在风电机组运行范围内没有共振点,不会引起严重共振现象,满足设计要求。
5 结论
本文以某兆瓦级风电机组传动链为例,绘制了机组传动链动力学拓扑图,根据德国劳埃德2010版风电机组认证规范的要求,建立了包括具有6个自由度刚柔耦合部件组成的机组传动链模型,该模型具有更多的自由度,仿真结果也更可信。此外,基于建立的机组传动链模型,进行了频域仿真分析,得到了机组传动链模态频率、绘制了二维Campbell图,找到了传动链潜在共振点,并通过时域扫频分析,验证了共振点的分析结果。通过与Bladed模型计算结果的对比,显示仿真分析得到的模态频率及能量分布的偏差在容许范围内,验证了模型和分析结果的正确性。
结果显示,某兆瓦级风电机组传动链在运行范围内没有共振点,不会引起严重共振现象,满足设计要求。
参考文献
[1]Feike Savenije,Koen Boorsma.Multi Body Simulations at ECN wind[DB].www.ecn.nl/units/wind.
[2]Berthold Schlecht.State of the art techniques used for determining reliable load assumptions in wind turbine using SIMPACK[DB].http://www.simpack.com/fileadmin/simpack/ doc/papers/SIMPACK_WIND_2010_IMM_Load_Assumptions.pdf.
[3]Schelenz,T Kamper.Aeroelastic rotors in multi-body simulation[DB].http://www.simpack.com/fileadmin/simpack/ doc/papers/SIMPACK_WIND_2010_RWTH_AerolasticRotors_n.pdf.
[4]Stefan Hauptmann,Denis Matha,Thomas Hecquet.Aeroelastic load simulations and aerodynamic and structural modeling effects[DB].
[5]Germanishcher Lloyd.Guideline for the Certification of Wind Turbines[S].2010:7-34.
[6]机械设计手册编委会.机械设计手册:第5卷[M].北京:机械工业出版社,2004.
[7]ANSYS.ANSYS Workbench 13 Help Documentation.
[8]Simpack.Simpack 8904 Help Documentation.
Research on Dynamics Modeling and Simulation Method of Drive Train for Mega-watts Wind Turbine
Liu Hua,Deng Liang,Yang Xiaolin
(Dongfang Electric Wind Power Co.,Ltd.,Deyang Sichuan,618000)
Abstract:A topology graph of the drive train for mega-watts wind turbine has been drawn and a multi-body dynamic model of the drive train has been built according to GL2010 guideline.Firstly,frequency-domain analysis has been conducted based on the model,the modal frequency of the drive train has been found,and 2D Campbell diagram has been generated to find the potential point of reso⁃nance.Secondly,the analysis result of resonance point has been verified by sweep analysis in time-domain.The correctness of the sim⁃ulation result has been verified by comparing with the Bladed result.
Key words:mega-watts wind turbine,drive train,dynamics simulation
中图分类号:TK83
文献标识码:A
文章编号:1674-9987(2016)02-0051-08
DOI:10.13808/j.cnki.issn1674-9987.2016.02.013
作者简介:刘桦(1975-),男,博士,副主任工程师,2009年毕业于重庆大学机械工程学院机械制造及其自动化专业,现主要从事风机整机及关键零部件设计工作。
