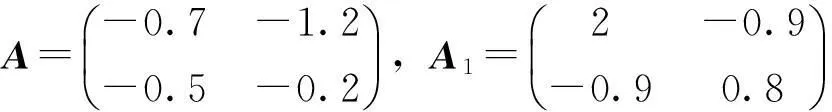基于随机模拟法的数学实验设计
2016-07-22高文华吴培浩崔超宇张宇风廖嘉祺
高文华,吴培浩,崔超宇,张宇风,廖嘉祺
(华南理工大学 a.数学学院;b.机械与汽车学院,广州 510640)
基于随机模拟法的数学实验设计
高文华a,吴培浩b,崔超宇b,张宇风a,廖嘉祺a
(华南理工大学a.数学学院;b.机械与汽车学院,广州510640)
摘要该文基于随机模拟法和Matlab编程,设计了布朗运动的模拟和对伊藤型随机微分方程解的数值仿真两个数学实验。设计的实验在丰富数学实验课程的教学内容的同时,使学生对随机过程微分方程有更深入的理解,有利于以创造性思维能力和自学能力为重点的学生综合能力的培养。
关键词数学实验;Monte Carlo方法;Matlab 仿真;随机微分方程
数学实验课是数学与计算机相结合的课程,更注重对学生应用数学能力的培养,强调学生自己动手做数学,也更能激发学生学习数学的积极性和兴趣。在数学实验中,由于计算机的引入和数学软件包的应用,为数学的思想与方法注入了更多、更广泛的内容,促进了数学同其他学科之间的结合,从而使学生有时间去做更多的创造性工作[1]。
随机现象在实际生活中广泛存在。随时间变化的各类系统受到不确定因素的作用,这些不确定因素往往服从某种统计规律,通常把这种具有统计规律的不确定因素称为随机因素。随机系统就是指用于描述这类受随机因素作用的时间过程的一类数学模型。这类数学模型一般是某些含随机过程的差分或微分方程[2]。随机微分方程能更真实、更准确地反映实际工程技术中的系统运动规律。随机控制理论也广泛地应用于经济、人口系统等社会领域以及航空航天、导航与控制、制造工程等工程领域。随机系统的研究已成为现代控制理论研究中的一个热点问题。
随机模拟法也叫Monte Carlo方法,它是用计算机模拟随机现象,通过大量的仿真试验,进行分析推断。概率论中的大数定理是数字特征随机模拟的理论根据。本文利用Matlab编程[3],设计了两个数学实验:布朗运动[4-6]的模拟和伊藤随机微分方程[7]的解的数值仿真。通过这些实验,可使学生对随机过程和随机微分方程有更深入的理解,也将激发学生学习数学的兴趣。
1 布朗运动的模拟实验
布朗运动是英国植物学家布朗在1827年首先发现的,他观察到悬浮在液体中的小粒子的扩散运动是极不规则的。1905年,著名物理学家爱因斯坦提出,布朗运动是由微小粒子与液体分子之间的碰撞引起的。1923年,维纳对布朗运动给出了严格的数学分析。布朗运动的第一个严格研究是维纳给出的,因此这种随机过程也称作维纳过程。维纳最重要的贡献是他对布朗运动过程的样本函数性质的研究,他证明了布朗运动的样本函数或轨道是连续的而且几乎处处不可微的函数。
自布朗运动发现以来,这个随机过程已在数理统计、经济学、量子力学、生物学、通信理论和管理科学等领域得到广泛运用。
标量布朗运动又称标准维纳过程,是指定义在区间[0,T]上的一个随机变量W(t),且满足下述3个条件:
(1)W(0)=0;
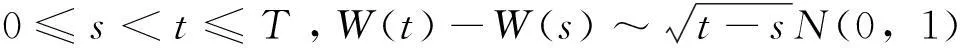
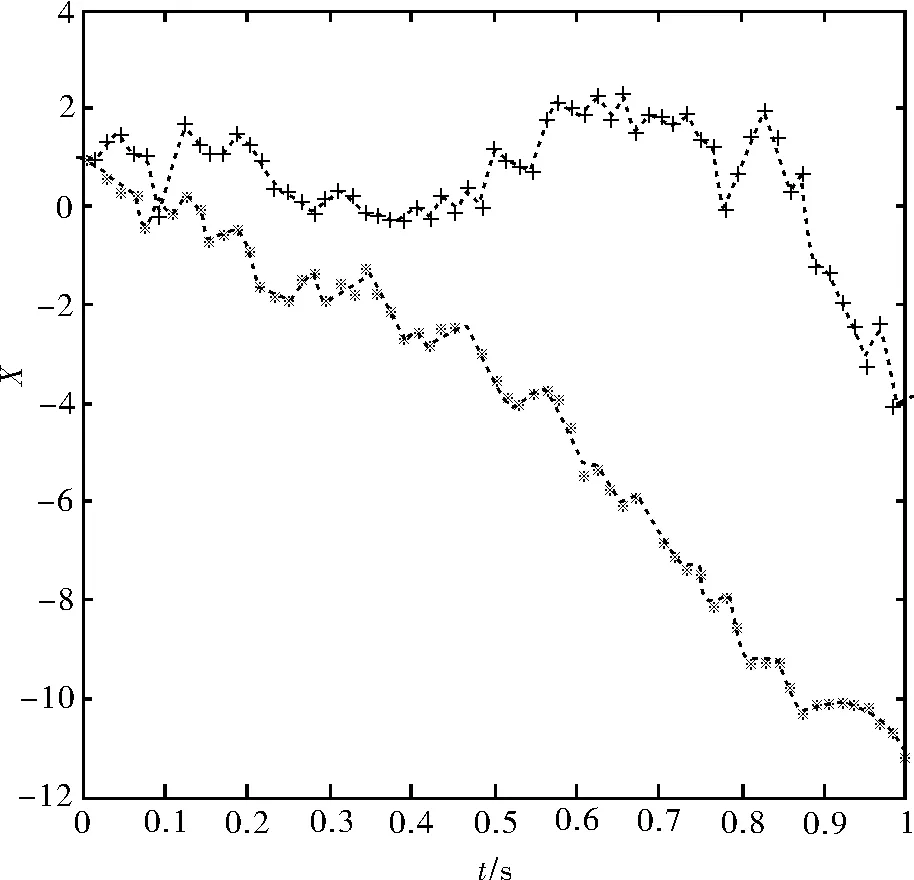
(3)对于0≤s 图1 对标量布朗运动的模拟 T=1; N=500; dt=T/N; dW=zeros(1,N); W=zeros(1,N); dW(1)=sqrt(dt)*randn; W(1)=dW(1); for j=2:N W(j)=W(j-1)+dW(j); end plot([0:dt:T],[0,W],′r-′); xlabel(′t′,′FontSize′,16); ylabel(′W(t)′,′FontSize′,16,′Rotation′,0); 可以将上述代码保存为m文件,程序的第一行为randn(′state′,200)时,不论在哪台计算机上运行得到的结论都如图1所示。如果把这个语句换为randn(′state′,sum(200*clock)),进行尽可能多次的模拟,会发现每一次的模拟得到的图形都不一样,都与之前的模拟无关,即体现了布朗运动的随机性。 2伊藤随机微分方程的解的数值仿真实验 伊藤型随机微分方程在工业、社会、经济领域都有广泛的应用,如在金融领域描述收益率波动的期权定价数学模型就是采用伊藤型随机微分方程,在工业领域为描述白噪声对系统的影响也是采用伊藤型随机微分方程。 对于随机微分方程而言,一般很难求出其具体解过程。因此,许多学者提出不同的数值策略,如Euler-Maruyama方法,向前、向后Euler-Maruyama方法,Taylor展式方法等。结合布朗运动的模拟,本文中主要运用Euler-Maruyama方法对伊藤随机微分方程的解进行数值仿真。 2.1简单的伊藤型随机微分方程解的数值仿真 例1简单的伊藤型随机微分方程 实验要求是使用Matlab编程对上述随机微分方程给出方程解的仿真曲线。 仿真程序如下,程序运行结果如图2所示。 randn(′state′,500) A=[1.1,-1.3;1.8,-2];X1zero = 1; T = 1;N = 2^8;dt = 1/N; randn(′state′,400); dWy=sqrt(dt)*randn(1,N); X(:,1)=1; for j = 1:L-1 Winc = [sum(dWx(R*(j-1)+1:R*j));sum(dWy(R*(j-1)+1:R*j))]; X(:,j+1) = X(:,j)+Dt*A*X(:,j)+ B*Winc; end plot(0:Dt:T,[X(1,1),X(1,:)],′r--*′),hold on plot(0:Dt:T,[1,X(2,:)],′g--+′),hold off xlabel(′t′,′FontSize′,12) ylabel(′X′,′FontSize′,16,′Rotation′,0,′HorizontalAlignment′,′right′) 图2 简单的伊藤型随机微分方程解的仿真曲线 2.2带有时滞的伊藤型随机微分方程解的数值仿真 例2带有时滞的伊藤型随机微分方程 实验要求使用Matlab编程对上述随机微分方程给出方程解的仿真曲线。 仿真程序如下,程序运行结果如图3所示。 图3 带有时滞的伊藤型随机微分方程解的仿真曲线 randn(′state′,200) A=[-0.7,-1.2;-0.5,-0.2]; B=[-1.6,-1.8;2.8,-1.4]; A1=[2,-0.9;-0.9,0.8];B1=[1.4,-2.5;0.07,-1.5]; T = 1;N = 2^8;dt = 1/N; Xem = zeros(1,L+5); Yem=zeros(1,L+5); X=[Xem;Yem]; for j = 1:L+5 if j<6; X(1,j)=sin(j-5)+1; X(2,j)=sin(2*(j-5))+1; else Winc = sum(dW(R*(j-6)+1:R*(j-5))); [X(:,j+1)]=X(:,j)+C*X(:,j+1-4)-C*X(:,j-4)+(A*X(:,j)+A1*X(:,j-4))*Dt+(B*X(:,j)+B1*X(:,j-4))*Winc; end end plot(0:Dt:T,X(1,(5:L+5)),′r--*′),hold on; plot(0:Dt:T,X(2,(5:L+5)),′b--+′),hold off; legend(′ x1图像′,′ x2图像′,1); xlabel(′t′,′FontSize′,12); ylabel(′x′,′FontSize′,16,′Rotation′,0,′HorizontalAlignment′,′right′) 3结束语 数学实验课程能够提高学生学习数学的积极性,培养学生应用数学的能力。基于科研与教学资源共享的原则,本文把科研中用到的仿真算法和例子编成了数学实验的案例,可以拓宽学生的视野,丰富数学实验课程的教学内容。 参 考 文 献 [1]焦光虹.数学实验[M].北京:科学出版社,2010. [2]韩崇昭,王月娟,万百五.随机系统理论[M].西安:西安交通大学出版社,1987. [3]赵景波.Matlab控制系统仿真与设计[M].北京:机械工业出版社,2010. [4]BRZEZNIAK Z,ZASTAWNIAK T.Basic stochastic processes[M].影印版.北京:清华大学出版社,2009. [5]陈六新.概率论与随机过程[M].北京:清华大学出版社,2013. [6]伊藤清.随机过程[M].上海:上海科学技术出版社,1961. [7]HIGHAM D J.An algorithmic introduction to numerical simulation of stochastic differential equations[J].Siam Review.2001,43(3):525-546. 收稿日期:2015-03-05;修改日期: 2015-03-25 基金项目:广东省高等学校教学质量与教学改革项目(x2lxN9120650);华南理工大学教研重点项目(x2lxY1130010)。 作者简介:高文华(1974-) ,女,博士,副教授,主要从事随机时滞系统的稳定性与控制方面的研究。 中图分类号O175;TP391.9 文献标志码A doi:10.3969/j.issn.1672-4550.2016.03.003 Mathematical Experiment Design Based on Random Simulation Method GAO Wenhuaa,WU Peihaob,CUI Chaoyub,ZHANG Yufenga,LIAO Jiaqia (a.School of Mathematics;b.School of Mechanical and Automotive Engineering,South China University of Technology,Guangzhou 510640,China) AbstractBased on Monte Carlo method and Matlab programming,two mathematical experiment cases are designed in this paper.One is the simulation of the Brownian movement,the other is the numerical simulation of the It� stochastic differential equation.These cases will enrich the content of mathematical experiment course as well as deepen the understanding of differential equation of random process.It would help the development of comprehensive ability of the students centering on creative thought ability and self-learning ability. Key wordsmathematical experiment;Monte Carlo method;Matlab simulation;stochastic differential equation