基于最优Hankel范数近似的核电站电功率与冷却剂平均温度解耦控制方法

钱　虹，　房振鲁，　杨祖魁，　周　蕾

(1.上海电力学院 自动化工程学院,上海 200090; 2.上海市电站自动化技术重点实验室，上海 200072)



基于最优Hankel范数近似的核电站电功率与冷却剂平均温度解耦控制方法

钱虹1,2，房振鲁1，杨祖魁1，周蕾1

(1.上海电力学院 自动化工程学院,上海 200090; 2.上海市电站自动化技术重点实验室，上海 200072)

摘要：采用最小二乘法获得了被控对象模型，针对核电站电功率和冷却剂平均温度控制耦合的特点，设计了对角阵完全解耦器，基于最优Hankel范数降阶模型近似的理论，对对角阵完全解耦器进行模型降阶，并在Matlab/Simulink中对所得到的模型进行仿真验证.结果表明：对对角阵完全解耦器降阶后的PID控制系统比单纯的PID控制系统的响应速度快，且进行功率控制时的超调量较小.

关键词：核电站； 最优Hankel范数近似； 解耦控制； 模型降阶

近年来，随着我国核能装机容量的迅速提升，核电站对我国局部地区电网负荷的贡献越来越大，在新形势下，核电机组越来越需要变工况运行,以满足电网不断增加的调频调峰压力[1].核电站由发电机、反应堆和汽轮机组成，是一个相互关联、强耦合的复杂多输入多输出的控制对象，具有纯滞后、大惯性和非线性的特点，其动态特性较为复杂.因此，当核电站变负荷运行时，核电站的2个重要控制参数，即冷却剂平均温度和电功率会产生耦合现象，使得核电机组的控制达不到理想的效果[2].由于核电站具有固定费用高而可变费用低的特点，我国核电站通常以带固定负荷的模式运行，国内针对核电站的研究大多集中在核电安全分析和风险控制上[3-7]，对核电站解耦控制的研究较少.笔者针对核电站变负荷运行时冷却剂平均温度和电功率控制中存在的耦合现象，根据核电站仿真机冷却剂平均温度和电功率控制的特点，研究设计对角阵完全解耦器以实现冷却剂平均温度和电功率的解耦控制，为核电站变负荷运行提供一种协调控制策略；同时采用最优Hankel范数降阶模型近似的方法对解耦器进行降阶处理[8]，并对降阶后的解耦器进行离散化以得到差分方程，有利于实际工程控制上的实现，以提高原控制系统的控制性能.

1核电站电功率与冷却剂平均温度的前馈解耦控制设计

1.1被控对象数学模型辨识

基于被控对象的数学模型，图1所示的核电站解耦控制方框图中的Gp11(s)、Gp21(s)、Gp12(s)和Gp22(s)分别表示阶跃信号下汽轮机阀门开度棒的电功率动态特性、汽轮机阀门开度棒的冷却剂平均温度动态特性、冷却剂平均温度调节棒(R棒)的电功率动态特性以及R棒的冷却剂平均温度动态特性.图1中的R1和R2分别表示电功率和冷却剂平均温度的输入信号，Gc1和Gc2为系统的控制器，N11(s)、N21(s)、N12(s)和N22(s)构成系统的对角阵完全解耦器，Y1为电功率输出，Y2为冷却剂平均温度输出,uc1(s)和uc2(s)为被控对象的输入信号.

图1　核电站解耦控制方框图

采用阶跃扰动进行模型辨识，主要基于以M310为参考堆芯的1 000 MW福清核电机组的仿真机，该核电站仿真机对堆芯中子、反应堆冷却剂系统以及核电站主系统均采用物理模型模拟系统全部的功能，其运行功能与实际现场情况具有近似1∶1的逼真度，在此模型基础上以满负荷功率(100%FP)运行时，分别对反应堆R棒和汽轮机进汽阀门加入阶跃信号，以获得被控对象的动态特性.

在仿真机上进行被控对象的阶跃响应实验，得到系统的输入和输出数据后，使用Matlab系统辨识工具箱中的arx函数完成最小二乘法的模型辨识，结果如图2所示.

由图2(a)～图2(d)的辨识结果分别得到模型的传递函数为：

(1)

(2)

(3)

(4)

其中，式(1)和式(2)分别为汽轮机阀门在阶跃扰动下，冷却剂平均温度的传递函数和电功率的传递函数；式(3)和式(4)分别为反应堆R棒在阶跃扰动下，冷却剂平均温度的传递函数和电功率的传递函数.

1.2对角阵完全解耦器设计

对角阵解耦是基于全解耦，要求被控对象特性矩阵与解耦环节的矩阵乘积等于对角阵，以实现完全解耦目的的.以图1所示的核电站解耦系统为例，说明对角阵完全解耦器的设计过程.

根据对角阵完全解耦器的设计要求，即

(5)

被控对象的输出变量与输入变量之间应满足以下方程：

(6)

假设被控对象传递矩阵Gp(s)为非奇异矩阵，于是得到解耦器的数学模型为：

(7)

将式(1)～式(4)代入式(7)中，得到核电站冷却剂平均温度和电功率的对角阵完全解耦器模型，如式(8)所示.

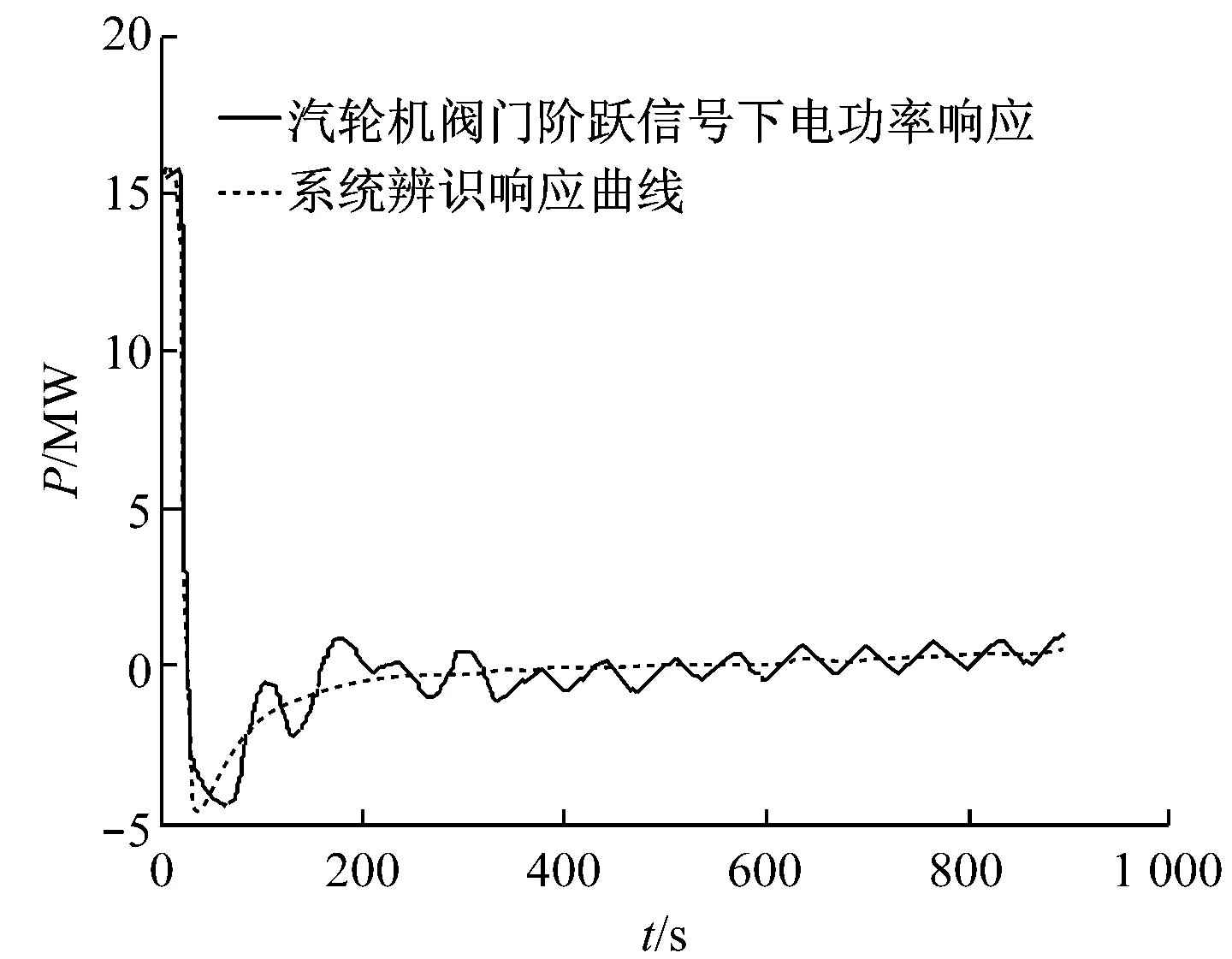
(a) 汽轮机阀门开度棒阶跃信号下电功率的动态特性及辨识

(b) 汽轮机阀门开度棒阶跃信号下冷却剂平均温度的动态特性及辨识

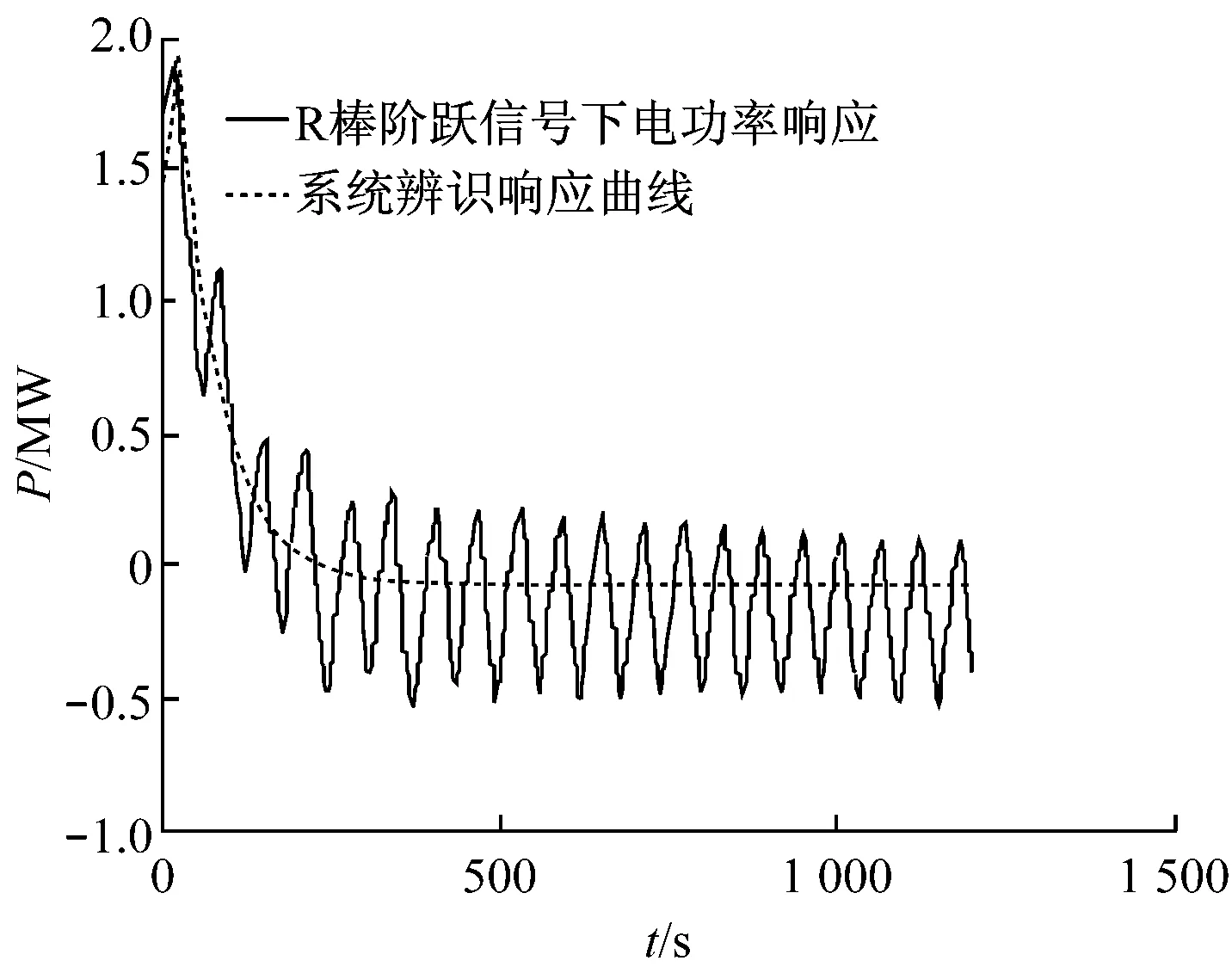
(c) R棒阶跃信号下电功率的动态特性及辨识

(d) R棒阶跃信号下冷却剂平均温度的动态特性及辨识

(8)

应用上述方法得到的解耦器维数高，直接对其进行分析相对困难，并且数字化处理耗时过长，因此，寻找一种能有效降低解耦器维数的方法尤为重要.笔者采用一种最优Hankel范数降阶模型近似的方法对解耦器进行降阶处理.

2最优Hankel范数降阶模型近似解耦器设计

2.1最优Hankel范数近似算法

英国学者Glover提出了求取给定状态方程模型的最优Hankel范数近似算法，该算法是系统模型降阶中的一种重要算法.最优Hankel范数近似算法原理如下.

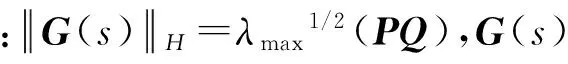
(9)

(10)

定义系统矩阵为：

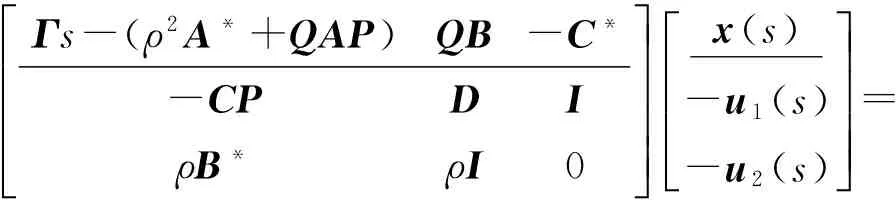
Γs-(ρ2A*+QAP)QB-C*-CPDIρB*ρI0éëêêêêùûúúúú x(s) -u1(s)-u2(s)éëêêêêùûúúúú=

(11)

其中，σk>ρ≥σk+1，Γ=QP-ρ2I.

式(11)有以下描述形式：

(12)

对于次优情况，即σk>ρ≥σk+1，Γ是可逆的，易求得式(12)的状态空间表达式：

(13)

考虑当ρ=σk+1时的最优情况，这时Γ为奇异矩阵，为了得到系统的状态空间表达式，要对Γ进行奇异值分解，并且求出与式(11)等价的状态空间表达式.可以得到：

(14)

2.2基于最优Hankel范数近似的核电站负荷跟踪控制解耦器算法

采用低阶模型可以简化对系统的理解，在仿真过程中可以减少计算量，使得设计控制器更加有效.对于使用对角阵解耦法设计得到的解耦器采用最优Hankel范数近似的方法进行降阶，得到以下解耦器的差分方程：

(15)

3核电站电功率与冷却剂平均温度解耦控制系统的仿真

基于Matlab/Simulink搭建降阶的解耦核电站负荷跟踪控制仿真系统，如图3所示.

图3　解耦降阶的核电站负荷跟踪控制系统仿真模型

3.1核电站电功率与冷却剂平均温度控制系统解耦仿真

核电站负荷跟踪控制系统为双输入双输出系统，基于对角阵完全解耦法得到解耦器，在Matlab/Simulink中搭建仿真系统，通过仿真阶跃扰动下的响应曲线验证解耦器的解耦效果，如图4所示.

通过对比图4(a)和图4(b)可以看出，解耦系统已将冷却剂平均温度的阶跃扰动对电功率的影响完

(a) 冷却剂平均温度控制信号阶跃扰动下耦合系统被控对象的响应曲线

(b) 冷却剂平均温度控制信号阶跃扰动下解耦系统被控对象的响应曲线

(c) 电功率控制信号阶跃扰动下耦合系统被控对象的响应曲线

(d) 电功率控制信号阶跃扰动下解耦系统被控对象的响应曲线

全补偿；通过对比图4(c)和图4(d)可以看出，解耦系统已将电功率的阶跃扰动对冷却剂平均温度的影响完全补偿.综上所述，解耦系统实现了核电站电功率和冷却剂平均温度控制上的完全解耦.

3.2基于最优Hankel范数近似降阶的系统仿真

用最优Hankel范数近似算法将控制系统解耦器降阶至2阶，在Matlab/Simulink中搭建仿真模型，实验结果如图5和图6所示.由图5可以看出，在阶跃扰动下，将解耦器降阶后系统电功率的变化曲线与完全解耦系统电功率的变化曲线基本吻合.由图6可以看出，在阶跃扰动下，将解耦器降阶后系统冷却剂平均温度的变化曲线与完全解耦系统冷却剂平均温度的变化曲线基本一致.这说明将解耦器降阶后对系统的解耦输出特性基本上没有影响，并且解耦器的维数下降到2维，降低了系统复杂度.

图5　阶跃扰动下电功率变化曲线

图6　阶跃扰动下冷却剂平均温度变化曲线

3.3核电站控制与基于最优Hankel范数降阶模型近似的解耦控制的仿真比较

核电站对冷却剂平均温度和电功率的控制并没有考虑系统耦合的情况.在Matlab/Simulink中分别搭建核电站PID控制模型、核电站解耦控制模型和核电站解耦降阶控制模型，仿真结果如图7和图8所示.由图7和图8可以看出，在电功率的控制中，解耦后的控制系统和解耦降阶后的控制系统的电功率输出曲线基本一致，而且均比未解耦的PID控制系统的电功率输出曲线的超调量小，响应速度快；在冷却剂平均温度的控制中，解耦后的控制系统和解耦降阶后的控制系统的冷却剂平均温度的输出曲线基本一致，虽然均较未解耦的PID控制系统的冷却剂平均温度输出曲线超调量稍大，但响应速度均较快.

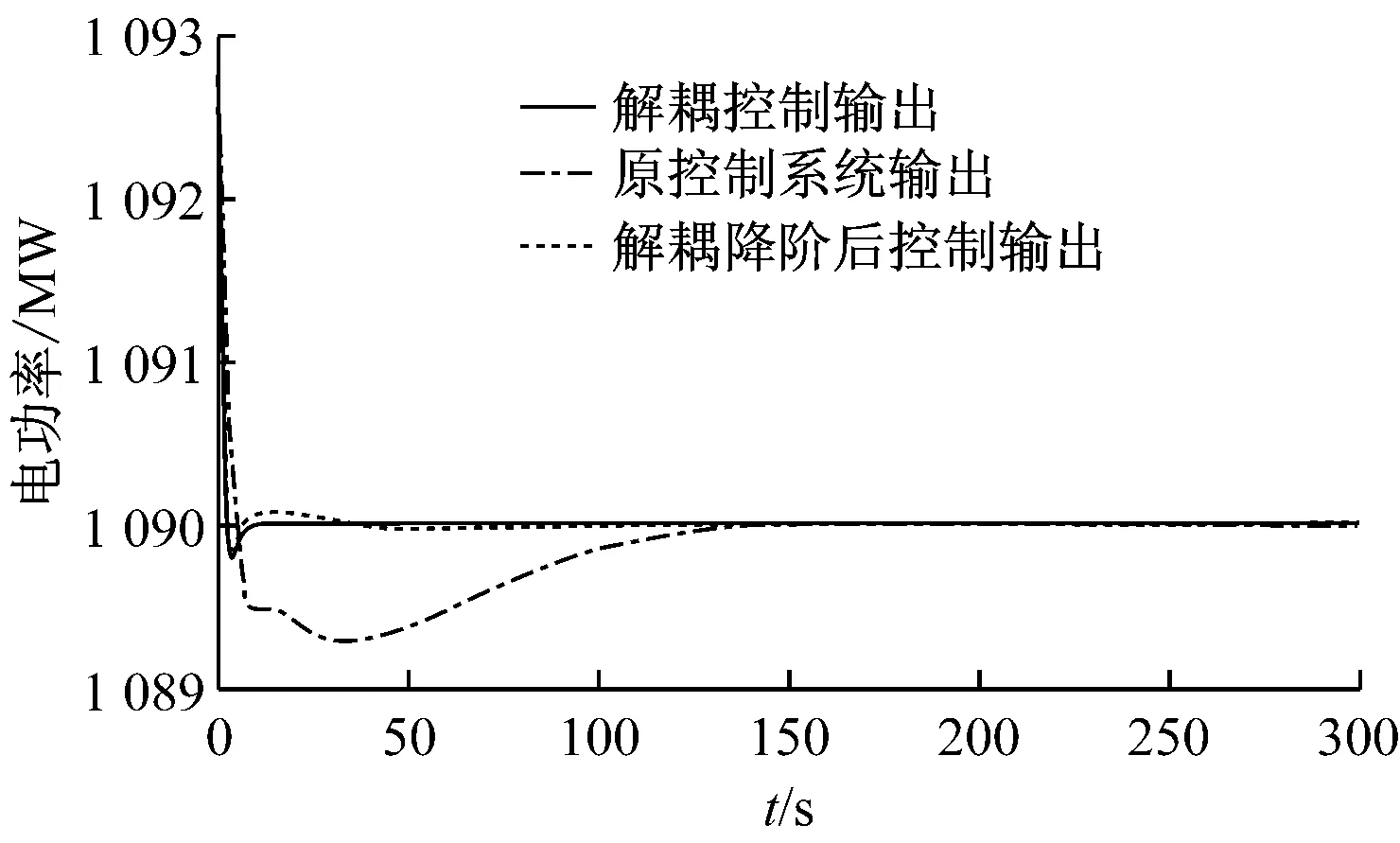
图7　电功率控制性能仿真曲线

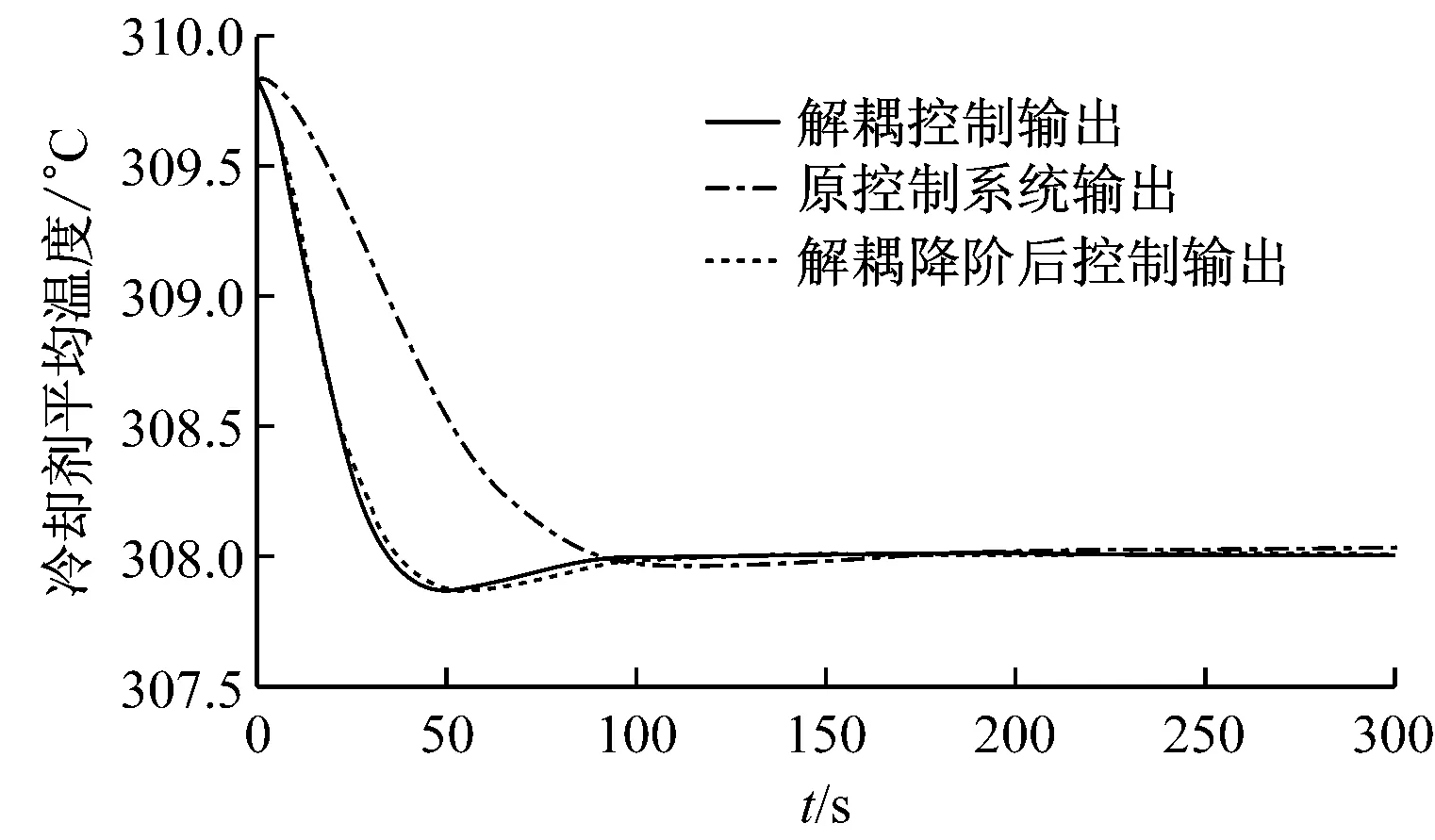
图8　冷却剂平均温度控制性能仿真曲线

4结论

针对核电站电功率和冷却剂平均温度控制的耦合特性，设计了对角阵解耦器进行完全解耦，仿真结果表明，解耦后的系统比单纯的PID控制系统的响应速度快，并且进行功率控制时的超调量较小.对解耦降阶后的控制系统在Matlab上进行仿真，仿真结果表明解耦降阶后的控制系统的控制效果与未降阶的解耦控制系统相差不大，但是解耦器的维数大大降低.将对角阵解耦、最优Hankel范数近似降阶和PID控制结合起来，不仅可以提高控制系统的性能，而且在工程实践中有良好的可行性.

参考文献：

[1]孙闻，徐衍会，陈世和，等．考虑核电调峰的广东电网机组组合[J]．南方电网技术，2012，6(3)：53-56．

SUN Wen, XU Yanhui, CHEN Shihe,etal. The unit commitment of Guangdong power grid in consideration of the nuclear power taking part in load regulation[J]．Southern Power System Technology, 2012，6(3)：53-56．

[2]席原, 刘景宾. 单元机组协调控制系统研究进展[J]. 工业仪表与自动化装置, 2011(5):10-16.

XI Yuan，LIU Jingbin. A review of coordinated control system for power units[J]. Industrial Instrumentation & Automation, 2011(5):10-16.

[3]吴宜灿, 胡丽琴, 李亚洲,等. 秦山三期重水堆核电站风险监测器研发进展[J]. 核科学与工程, 2011, 31(1):68-74.

WU Yican, HU Liqin, LI Yazhou,etal. Development of Third Qinshan nuclear power plant risk monitor[J]. Nuclear Science and Engineering, 2011, 31(1):68-74.

[4]董毅漫, 张弛, 宋大虎,等. 我国核电安全目标发展取向的思考[J]. 核安全, 2012(4):10-15.

DONG Yiman, ZHANG Chi, SONG Dahu,etal. Thinking of nuclear power safety goal development orientation in China[J]. Nuclear Safety, 2012(4):10-15.

[5]郑智敏. 核电厂汽轮机跳机风险控制与管理方法探讨[J]. 中国高新技术企业旬刊, 2015(2)：84-86.

ZHENG Zhimin. Discussion on risk control and management method of the steam turbine of the nuclear power plant[J]. China High-Tech Enterprises, 2015(2)：84-86.

[6]孙铭遥. 中国核电工程项目风险管理研究[D]. 长春：吉林大学, 2013.

[7]邓德兵, 赵清森, 陈伟,等. 核电站汽轮机运行性能监测与诊断[J]. 动力工程学报, 2011, 31(8):585-589.

DENG Debing, ZHAO Qingsen, CHEN Wei,etal. Performance monitoring and fault diagnosis of wet-steam turbines for nuclear power plants[J]. Journal of Chinese Society of Power Engineering, 2011, 31(8):585-589.

[8]童东兵. 受控系统模型降阶及其稳定性研究与应用[D]. 上海：东华大学, 2013.

Decoupling Control on Electric Power and Average Refrigerant Temperature of Nuclear Power Stations Based on Optimal Hankel-norm Approximation

QIANHong1,2,FANGZhenlu1,YANGZukui1,ZHOULei1

(1.School of Automation Engineering, Shanghai University of Electric Power, Shanghai 200090, China;2. Shanghai Key Laboratory of Power Station Automation Technology, Shanghai 200072, China)

Abstract：Based on the objective model obtained using least-square method, a complete decoupler of diagonal matrix was designed according to coupling features of the electric power and average refrigerant temperature in a nuclear power station, to which the model order was reduced on the basis of optimal Hankel-norm approximation, and the model thus obtained was subsequently verified with Matlab/Simulink. Results show that the PID control system of order-reduced diagonal matrix is faster in response with lower overshoot in power control, compared with the simple PID control system.

Key words：nuclear power station; optimal Hankel-norm approximation; decoupling control; model reduction

收稿日期：2015-07-10

修订日期：2015-08-21

基金项目：上海市重点实验室电站自动化技术实验室资金资助项目(04DZ05901)

作者简介：钱虹(1967-)，女，上海人，副教授，博士，研究方向为核电站检测与控制.

文章编号：1674-7607(2016)05-0383-06中图分类号：TP13

文献标志码：A学科分类号：510.80

房振鲁(通信作者)，男，硕士研究生，电话(Tel．)：18301791276；E-mail：fangzhen_lu@163.com.