核反应堆功率控制研究

刘文杰，　叶建华

(上海电力学院 自动化工程学院，上海 200090)



核反应堆功率控制研究

刘文杰，叶建华

(上海电力学院 自动化工程学院，上海 200090)

摘要：通过对核反应堆进行分析，建立其数学模型，并在此基础上进行PID控制与模糊PID控制，分析了2种控制方式的优缺点.将2种控制策略进行整合，使核反应堆的控制模式可以在2种控制方式下切换.结果表明：将控制策略整合后，核反应堆功率控制的响应时间、超调量和鲁棒性等效果都得到明显的优化提升.

关键词：核反应堆； 数学模型； PID控制； 模糊PID控制； 复合控制

在全球经济高速发展的同时，能源需求量也与日俱增.核电作为一种高效、清洁能源，在各种发电能源中的地位日益上升.为促进经济、社会的可持续发展，保证国家能源供应与安全，必须加快能源结构调整，高度重视核电的开发和利用，加强核电建设已成为我国能源建设的一项重要政策.

核电站的正常工作状态一般可分为2种：固定功率输出的A模式和根据用电负荷改变输出功率的变功率输出的G模式.随着核电站的发展，对核电站发电性能要求越来越高.核电机组不能仅保持原有的A模式，核电机组的功率也应根据需求电量的变化进行相应的调整.核反应堆功率与核反应堆温度的变化息息相关，核反应堆温度的变化将直接影响蒸汽发生器蒸汽量的输出，从而对涡轮机的蒸汽输出造成影响，进而影响整个核电站的发电量.

正确调节核反应堆功率和冷却剂温度是实现核电机组安全、高效和稳定运行的必要条件.目前大部分核反应堆控制都是根据汽轮机负荷来控制反应堆冷却剂平均温度的.常规控制方法易于实现且操作简单，被广泛用于工业现场，但常规控制方法的调节性能难以对核反应堆功率做出精确控制，亟需提出新的控制策略来提高核反应堆功率的控制精度.

1建立核反应堆的数学模型

1.1核反应堆的数学分析

根据缓发中子的平均寿期和衰变常数等的不同，目前国际核工业界将缓发中子大致划分为6组(缓发中子组数G=6)，但只有一组缓发中子的反应堆模型(G=1)可以作为近似物理模型，用来阐述反应堆的基本原理.依据单组缓发中子模型设计的控制器可以很好地适用于由6组缓发中子模型构成的高阶系统.因此，笔者应用单组缓发中子(G=1)的点堆中子动力学方程设计控制器.

假定空间形状函数不随时间改变，在不考虑外加中子源、反应性反馈和氤毒反馈的情况下，建立核反应堆的中子动力学方

(1)

其中，

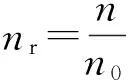
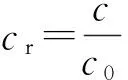
式中：n为中子密度；n0为初始中子密度；nr为中子密度与初始中子密度的相对值；ρ为反应性核素，单位为Bq/g；β=0.006 5，为缓发中子的总份额；Λ=0.000 1 s，为中子的平均寿命；c为缓发中子先驱核浓度；c0为缓发中子的初始浓度；cr为缓发中子先驱核浓度与初始浓度的相对值；λ=0.125，为中子先驱核的衰变常数；Gr=0.01为控制棒相对位移量；zr为控制棒的速度.

式(1)为二阶非线性系统模型.笔者在本文中只考虑单组缓发中子的点堆中子动力学方程，以达到对系统进行分析并设计控制器的目的[2].因此，每当引入一个Δnr，就会使cr=Δc+c0、ρ=Δρ+ρ0，ρ0为反应性核素的初始值；zr=Δz+z0，z0为控制棒的初始速度.在平衡条件下ρ0=0,z0=0，可将式(1)转化为线性化后的点堆中子动力学方程，如式(2)所示：

(2)

式(2)可简单、直观地描述核反应堆功率系统，其控制系统状态结构图[3]如图1所示.

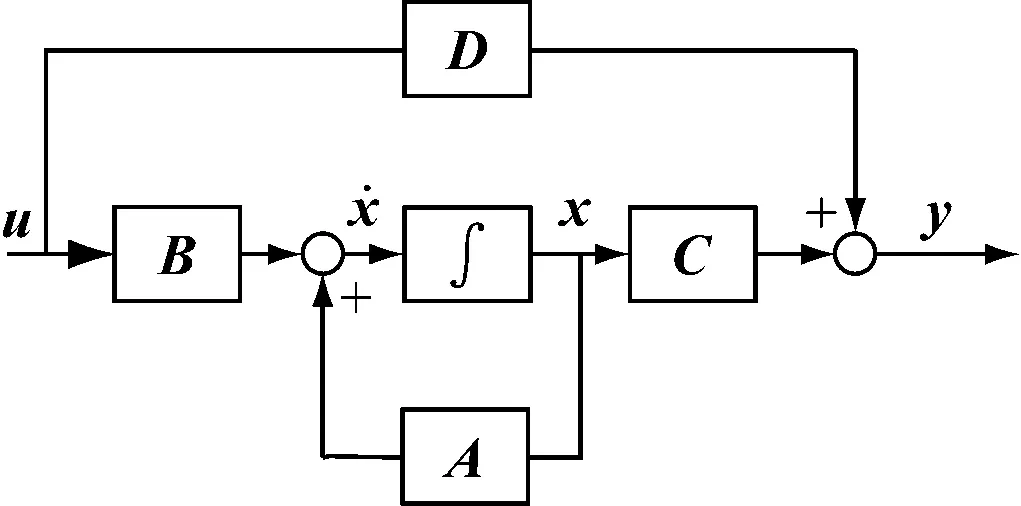
图1　控制系统状态结构图

为建立核反应堆状态方程，需将式(2)转化成如下状态空间表达式[4]：

(3)

其中，

根据自动控制原理，由连续时间系统的状态空间表达式可求出系统的开环传递函数.因此，由式(3)可求出反应堆的开环传递函数，其求解式为[5]：

(4)

1.2配置状态反馈矩阵

若要使系统达到稳定控制的效果，必须为开环传递函数加一个反馈矩阵.在使用极点配置方法的状态反馈设计中，系统的动态特性可以任意设定.状态反馈设计的闭环极点在根轨迹图中没有约束，可以在复平面中任意选取[6].笔者将3个极点设置为-1+j，-1-j，-15，可将状态结构图转化为图2所示，其中，F=(f1,f2,f3)，为状态反馈矩阵；V=f1+f2[7]，为前馈增益系数.通过Matlab中系统状态反馈极点配置函数acker求解.

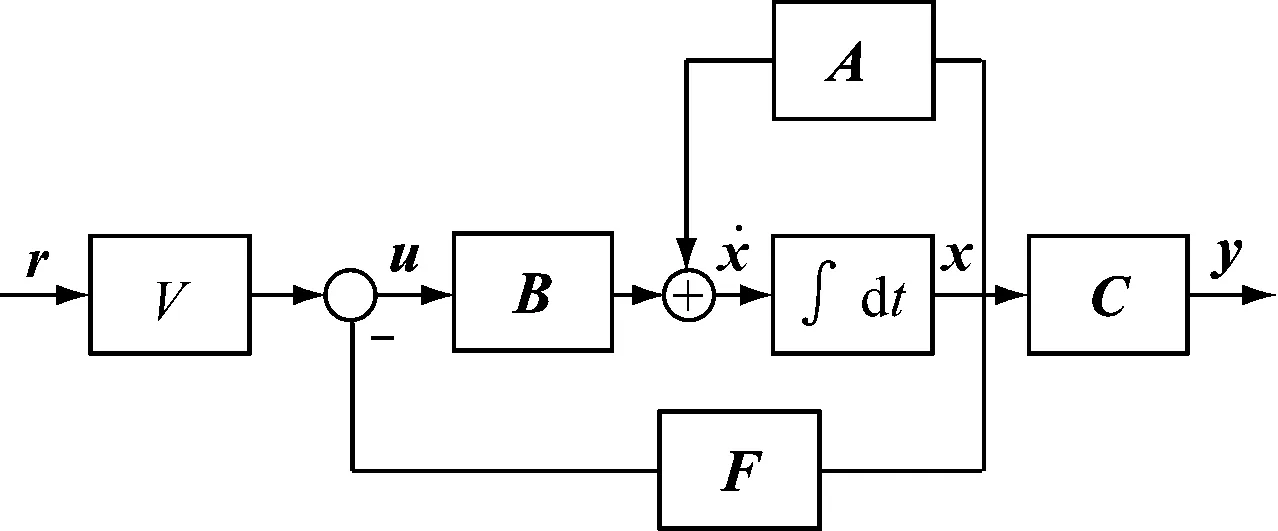
图2　状态结构图

1.3建立核反应堆数学模型

图2所示的状态结构图由2个负反馈组成，通过状态反馈矩阵F的引入可将图2中的变量进一步转化为:

(5)

(6)

(7)

于是可得到核反应堆的闭环传递函数：

(8)

2PID控制

传统PID控制具有一套完整的参数整定与设计方法，易于实现和现场操作，许多工业回路对控制系统的快速性和控制精度要求不高，而是更重视系统的可靠性，因此使用传统PID控制能获得较高的性价比.

传统PID控制器可描述为[8]：

(9)

其中，比例系数Kp能够提高系统的响应速度和精度；积分系数Ki能够消除静态误差；微分系数Kd用于改进系统的动态性能[9]；e(t)为系统设定值与输出值之间的偏差量.

将核反应堆初始功率设置为600 MW，在Simulink下对核反应堆系统进行建模，仿真时间为1 s，得到的传统PID控制结果如图3所示.

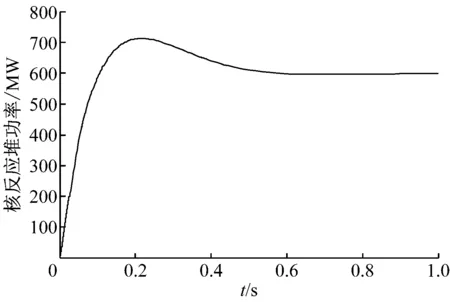
图3　传统PID控制结果

由图3可知，传统PID控制在0.6 s左右达到稳定，在0.1 s左右第一次达到设定值，具有较大的超调量，不能精确地控制核反应堆功率.

3模糊PID控制

3.1制定模糊控制规则

模糊控制是一种利用专家经验，运用语言变量和模糊集合理论的控制理论.将模糊规则以及相应的控制经验预先存储到计算机的知识库中，使计算机能够依据控制系统的响应情况进行模糊推理，得到相应的输出[10].

核反应堆控制系统利用传统PID控制难以达到相应的精度要求.利用模糊控制规则对传统PID控制器参数进行实时调整，可以有效地将模糊控制以及传统PID控制结合起来.使传统PID控制器可以根据功率响应情况做出实时调整，以达到更加优化的控制效果.具体方法如下：

(1) 采用模糊控制方法建立模型，将偏差信号E和偏差变化量Ec作为输入，传统PID控制器参数的修正量作为Kp、Ki和Kd的输出.根据E和Ec实际的基本论域,设定E和Ec论域[11].选择传统PID控制器3个参数Kp、Ki和Kd的调整量作为模糊控制的输出.将传统PID器控制的Kp、Ki和Kd相加得到输出量，达到优化控制.

(2) 划分语言变量和隶属度函数.将各模糊变量的语言变量均划分为正大(Positive Large，PL)、正中(Positive Middle，PM)、正小(Positive Small，PS)、零(Zero，Z)、负小(Negative Small，NS)、负中(Negative Middle，NM)和负大(Negative Large，NL).各语言变量在论域上的模糊子集隶属度函数完全相同.正大、负大均采用高斯函数，其他采用三角函数.

(3) 指定模糊控制规则，各控制规则如表1～表3所示[12].

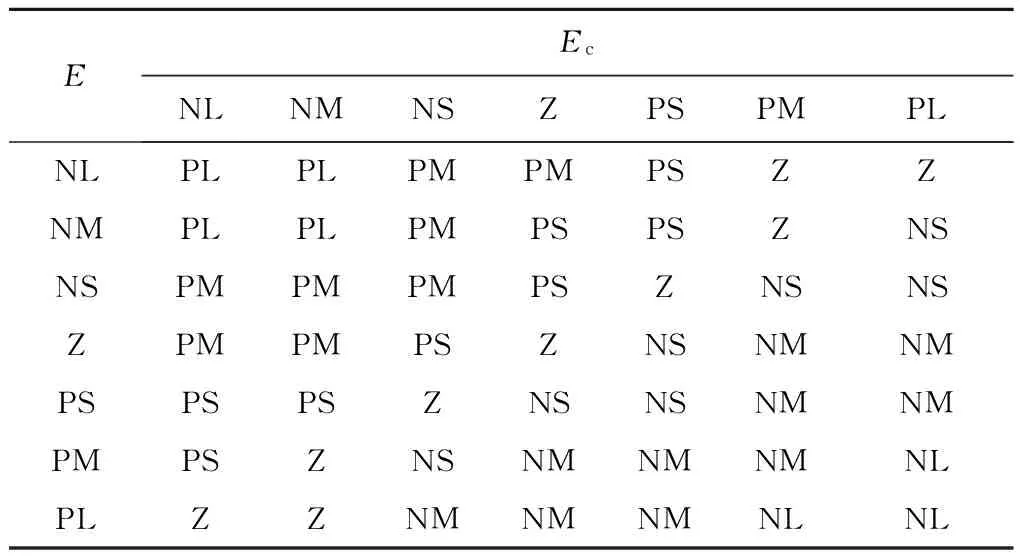
表1　比例系数Kp的模糊规则表

(4) 去模糊化.对模糊控制器的输出和传统PID控制器参数进行调整，以达到最优化的控制器输出[13].

将模糊PID控制应用于核反应堆模型的控制中，在Simulink中建立仿真模型，将仿真时间设为2 s，与传统PID控制进行对比，结果如图4所示.

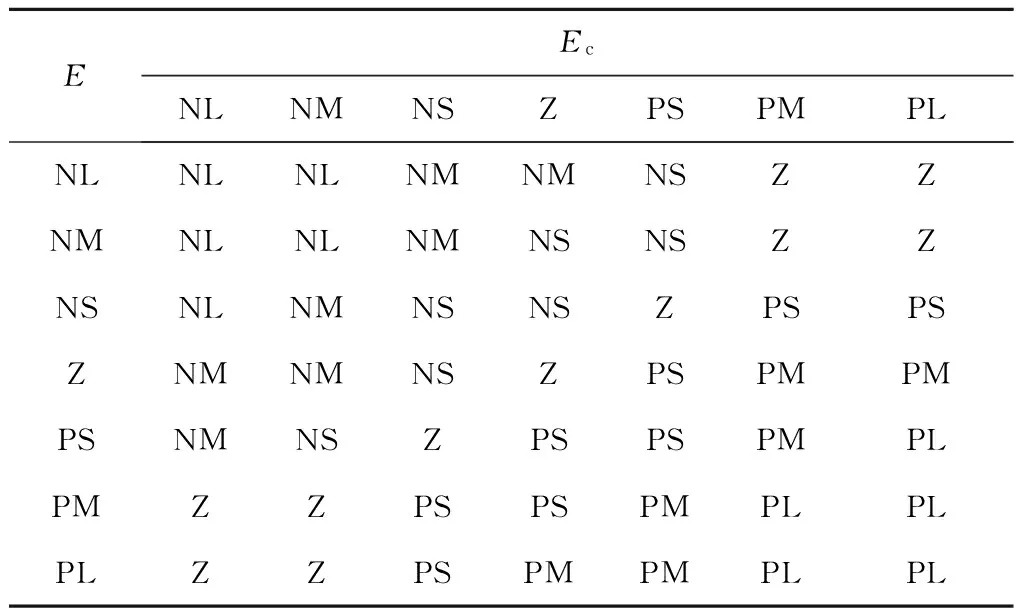
表2　积分系数Ki的模糊规则表

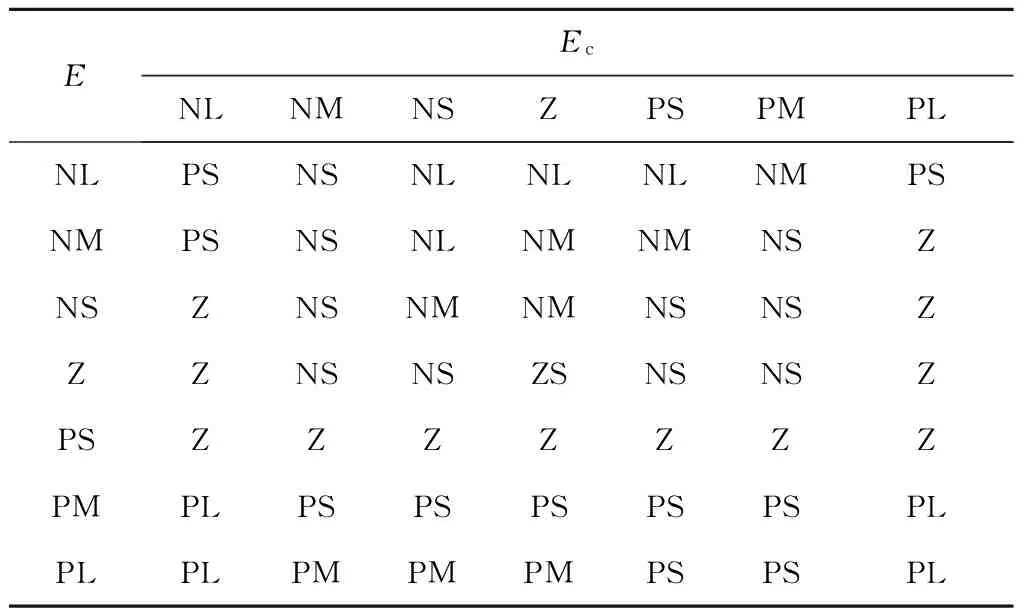
表3　微分系数Kd的模糊规则表

图4　模糊PID控制结果图

由图4可以看出，模糊PID控制结果超调量明显减小，较传统PID控制的20%减小至10%，且第1次达到设定值的时间约为0.04 s.整个过程功率波动很小，控制效果有明显提升.但其控制过程具有较长的调节时间，在1.3 s左右才达到稳定，较传统PID控制的稳定性差.若通过修改参数或改变控制规则使调节时间变短，则模糊PID控制的稳定性和响应的快速性会相应减弱.

3.2复合控制

传统PID控制具有在短时间内达到稳定状态的优点，而模糊PID控制则具有响应速度快、超调量小的优点.将2种控制策略的优点集中起来可极大地提升控制效果[8].

将2种控制方式均应用在核反应堆功率控制的模型上，需要一个适合控制的变量以实现在2种控制策略之间进行切换.通过对模型进行仿真实验时各种变量的比较发现，功率反馈偏差信号E的变化适合2种控制策略之间的切换.通过添加switch开关，在对反应堆模型进行仿真实验时，根据偏差值的变化，对功率反馈偏差信号E进行控制，使控制模式得到切换.功率反馈值与功率设定值之间的偏差信号E的变化曲线如图5所示.

图5　偏差信号E的变化曲线

由图5可知，在模糊PID控制效果良好的前0.5 s内，偏差信号E的绝对值均较大.因此将偏差信号E的绝对值作为控制器switch的输入信号，将仿真时间设为1 s，仿真结果如图6所示.

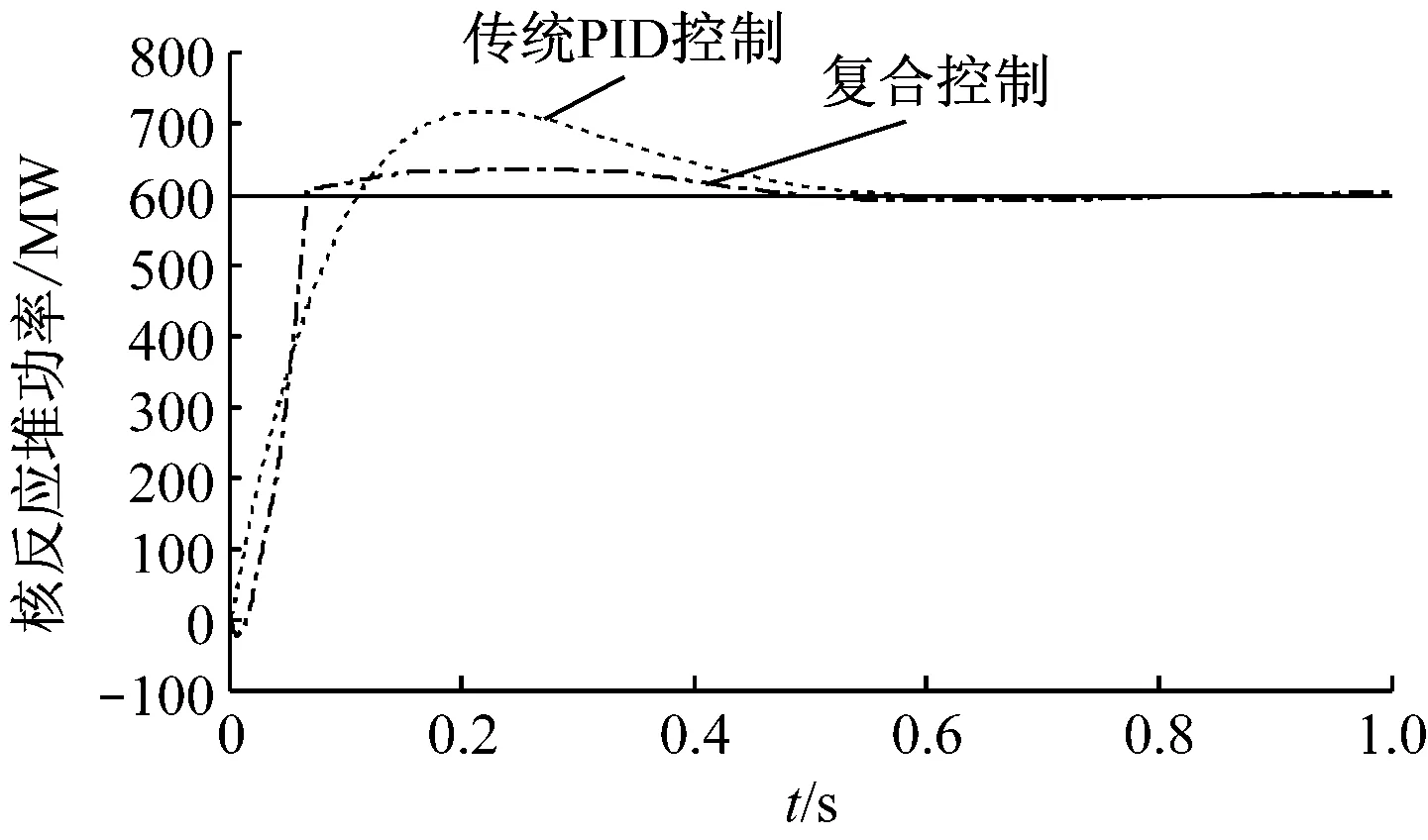
图6　复合控制曲线

由图6可以看出，加入switch开关的复合控制效果得到了明显提升，不仅具有模糊PID控制的低超调量、快速响应的优点，其调节时间也缩短为0.6 s左右.

在针对偏差信号E的控制中，偏差信号E2次穿越0值，其中一次在前0.3 s内，如果在这段时间内进行控制切换会降低控制效果.因此，在原来模型的基础上，将switch开关的输入量变为简单的模糊控制，输入变量为E和Ec，输出为模糊控制器的输入信号，设定模糊控制规则，避免偏差信号E在第一次达到0值附近时就切换控制方式.

在Simulink中改变模型，将仿真时间设为1 s，得到如图7所示的控制效果.

由图7可以看出，改进后的控制效果得到明显提升，核反应堆功率在0.15 s时达到稳定，且超调量由模糊PID控制的10%降低至4%左右，响应速度有很大提升，可满足核电站在变功率负荷需求情况下的控制要求.

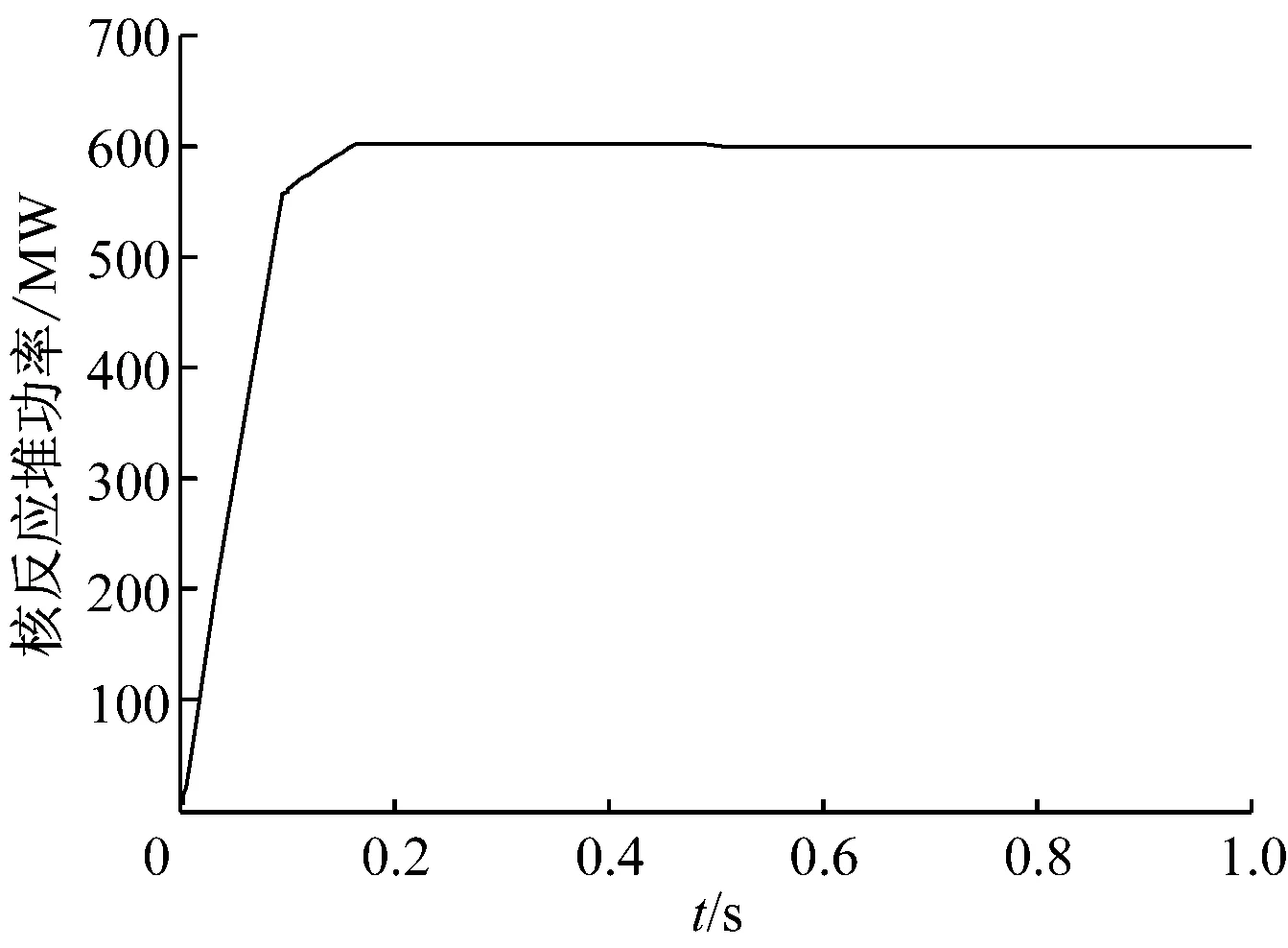
图7　改进后的控制结果

4结论

(1) 通过在Matlab仿真环境下建立核反应堆控制模型，并进行PID控制实验和模糊控制实验，发现模糊控制较传统PID控制具有更快的响应速度和更小的超调量.

(2) 通过对控制过程中偏差变量E的控制，使核反应堆功率控制模型可以在传统PID控制与智能模糊控制之间切换，以达到更加优化的控制效果.

参考文献：

[1]杨平，梁火南，陈岩，等.核反应堆功率的协调型标准传递函数控制 [J].动力工程学报，2014, 34(8)：624-627.

YANG Ping，LIANG Huonan，CHEN Yan，etal. Standard transfer function control for power of nuclear reactors[J]. Journal of Chinese Society of Power Engineering,2014, 34(8)：624-627.

[2]陈宇中,杨凯军,沈永平.核反应堆模糊PID控制的实验模拟系统[J].核动力工程,2000,21(6)：528-531.

CHEN Yuzhong, YANG Kaijun, SHEN Yongping. Experimental simulation system of fuzzy PID control on nuclear reactor[J]. Nuclear Power Engineering,2000,21(6)：528-531.

[3]刘磊，栾秀春，饶甦，等.模糊鲁棒控制方法在核反应堆功率控制中的应用[J].原子能科学技术,2013,47(4)：624-629.

LIU Lei， LUAN Xiuchun， RAO Su,etal. Application of robust fuzzy control in power control of nuclear reactor[J]. Atomic Energy Science and Technology, 2013, 47(4)：624-629.

[4]武红幸，赵福宇，张仲民．新型模糊控制器在小型反应堆功率控制系统中的应用[J].核动力工程, 2008,29(5):80-82.

WU Hongxing, ZHAO Fuyu, ZHANG Zhongmin. Application of new fuzzy controller to small nuclear reactor power control system[J].Nuclear Power Engineering, 2008, 29(5):80-82.

[5]毛伟, 张宇声, 张广福. 压水型核反应堆功率控制系统的优化设计[J].海军工程大学学报,2005,17(2):88-91.

MAO Wei, ZHANG Yusheng, ZHANG Guangfu. Optimal design of power control system of PRW[J].Journal of Naval University of Engineering, 2005,17(2):88-91.

[6]TANAKA K,WANG H O. Fuzzy control systems design and analysis:a linear matrix inequality approach[R].New York, USA: John Wiley & Sons,Inc,2001.

[7]MASUBUCHI I， KAMITANE Y， OHARA A.H∞control for descriptor systems: a matrix inequalities approach[J].Automatica,1997,33(4):669-673.

[8]成守宇, 彭敏俊, 刘新凯. 免疫P-PID串级控制的核反应堆功率调节器研究[J].核动力工程,2014, 35(5):39-42.

CHENG Shouyu, PENG Minjun, LIU Xinkai. Research on reactor power controller based on artificial immune P& PID cascade control technology[J]. Nuclear Power Engineering, 2014, 35(5):39-42.

[9]欧怀谷, 李富, 张良驹，等. 核反应堆功率控制系统的数字化实现[J].原子能科学技术，2004,38(S):1-5.

OU Huaigu, LI Fu, ZHANG Liangju,etal. A digitalized power control system for nuclear reactor[J]. Atomic Energy Science and Technology, 2004, 38(S):1-5.

[10]栾秀春, 周杰, 杨爱民，等. 基于Takagi-Sugeno模糊模型的核反应堆功率积分控制系统[J].中国电机工程学报,2013,33(2):105-111.

LUAN Xiuchun, ZHOU Jie, YANG Aimin,etal.Integral control system of nuclear reactor power based on Takagi-Sugeno fuzzy model[J]. Proceedings of the CSEE,2013,33(2):105-111.

[11]邓琛, 张琴舜. 双线性控制技术在反应堆功率调节系统中的应用[J].上海交通大学学报,1997,31(9):149-151.

DENG Chen, ZHANG Qinshun. Application of bilinear control technology in nuclear reactor power adjustment system[J].Journal of Shanghai Jiaotong University, 1997,31(9):149-151.

[12]DONG Zhe, HUANG Xiaojin, ZHANG Liangju. Output-feedback load-following control of nuclear reactors based on a dissipative high gain filter[J].Nuclear Engineering and Design, 2011,241(12):4783-4793.[13]Third Qinshan Nuclear Power Co., Ltd., CNNC. Project construction and important technical innovation for Qinshan Phase Ⅲ (PHWR) nuclear power plant[J]. Engineering Sciences,2007, 5(4):98-117.

Study on Power Control of Nuclear Reactors

LIUWenjie,YEJianhua

(School of Automation Engineering, Shanghai University of Electric Power, Shanghai 200090, China)

Abstract：A mathematical model of nuclear reactor was built based on numerical simulation, and subsequently PID and fuzzy-PID controls were simulated with the model, while advantages and disadvantages of the two control methods were analyzed. By integrating the two control strategies, a compound control mode was proposed for the nuclear reactor, in which case, the control can be switched between the above two methods. Results show that through integration of the two methods, the effects of power control are significantly optimized and improved in the aspects of response time, overshoot and robustness, etc.

Key words：nuclear reactor; mathematical model; PID control; fuzzy-PID control; compound control

收稿日期：2015-06-30

修订日期：2015-08-11

作者简介：刘文杰(1990-)，男，山东烟台人，硕士研究生，研究方向为核电站运行控制和控制理论与控制工程.电话(Tel.)：15601951799；E-mail：15601951799@163.com.

文章编号：1674-7607(2016)05-0378-05中图分类号：TP13

文献标志码：A学科分类号：510.80