循环流化床锅炉床温的预估滑模控制

朱红霞，　沈　炯，　李益国

(1． 东南大学 能源与环境学院， 南京 210096； 2． 南京工程学院 能源与动力工程学院， 南京 211167)



循环流化床锅炉床温的预估滑模控制

朱红霞1,2，沈炯1，李益国1

(1． 东南大学 能源与环境学院， 南京 210096； 2． 南京工程学院 能源与动力工程学院， 南京 211167)

摘要：针对大惯性、大滞后热工过程因负荷、煤种和环境条件的改变以及模型简化等带来的不确定性，设计了一种便于运行人员理解和工程实现的预估滑模控制方案.首先基于标称工况下辨识得到的二阶加纯滞后(SOPDT)模型，构建一个无迟延输出预估模型，用于过程输出值的预测，然后通过合理设计滑模函数和不确定上界自适应估计的滑模控制律，使得具有不确定性的闭环系统能在任何外扰的作用下保持渐进稳定.针对循环流化床锅炉床温对象的仿真实验结果表明：采用该预估滑模控制方案的床温控制系统调节速度快、超调量小且具有很强的抗干扰能力.

关键词：预估滑模控制； SOPDT模型； 不确定性； 循环流化床； 床温

由于循环流化床(CFB)锅炉具有燃烧效率高、燃料适应性广和低污染等优点[1]，因而近年来在国内外受到广泛重视，并得到迅速发展.CFB锅炉在动态特性上不同于煤粉炉和重油炉，主要表现在锅炉燃烧室内流化层大容量的热平衡特性.床层温度是直接影响CFB锅炉能否安全连续运行的重要控制参数，为保证锅炉处于最佳燃烧条件，运行时床温一般控制在850～950 ℃，此时炉内脱硫效率高且NOx的生成量小.目前，工程上CFB锅炉床温控制系统大多采用传统的PID控制方法；理论研究方面，模糊控制[1-2]、自抗扰控制[3]和预测控制[4-5]等先进控制方法已被应用到床温控制中.

采用CFB锅炉的机组一般均会直接参与调峰，因而会频繁变负荷运行.一些电厂在煤炭供应紧张期间，其燃料来源多样化，导致煤质经常发生变化.运行工况的调整、煤质的变化、环境的改变以及控制系统设计中对模型的简化和近似等，都不可避免地给系统带来各种不确定性，而且这些不确定性还会随着系统动态的演化而改变，从而严重影响控制系统的实际性能.应对不确定性的影响，一种可行的控制策略是采用鲁棒控制，但目前采用较多的H∞鲁棒控制等方法理论性较强，不利于运行人员的理解和工程实现.滑模控制(SMC)是一种特殊的鲁棒非线性控制器，由于滑动模态可以进行设计且与对象参数及扰动无关，所以SMC具有响应快速、对参数变化及扰动不灵敏、无需系统在线辨识和物理实现简单等优点[6-7].鉴于滑模控制在处理不确定性和抗干扰方面的绝对优势，笔者针对CFB锅炉床温等复杂热工对象，从便于工程实际应用的角度出发，设计了一种简单而新颖的预估滑模控制方案，并通过仿真实验验证了其有效性.

1CFB锅炉床温被控对象的动态特性

CFB锅炉运行过程中影响床温的因素很多，如给煤量、一次风量、二次风量、石灰石量、排渣量和返料量等.目前，国内的CFB锅炉主要通过给煤量和一次风量进行床温调节.仇韬[8]以金陵石化热电厂的6号炉(220 t/h循环流化床锅炉)为试验对象，在不同负荷和不同煤种情况下对其动态特性进行了分析，并给出不同工况下的床温对象模型.

给煤量-床温通道的传递函数(未考虑给煤的传输迟延)为：

(1)

一次风量-床温通道的传递函数为：

(2)

式中：KB和KF均为静态增益；τB、TB、τF和TF为时间常数，均随运行工况的不同而变化.

仇韬[8]通过相关性分析和不同工况下的仿真计算，建立了式(1)和式(2)中的各参数与负荷和煤种性能指数之间的关系，利用函数关系可以直接根据负荷和煤质确定出当前工况下CFB锅炉床温对象的传递函数模型.但其提供的模型未考虑燃料的传输迟延.若考虑传输迟延，给煤量-床温通道的动态特性可表示为：

(3)

式中：τ0为给煤量在传输环节的迟延时间，s.根据实际经验，近似估计τ0=30 s.

表1给出了CFB锅炉在90%、80%和70% 3个不同负荷下分别采用大同烟煤、阳山无烟煤和兴隆褐煤时床温的传递函数模型参数.图1给出了在不同负荷和不同煤种下，给煤量阶跃扰动和一次风量阶跃扰动下床温的动态响应特性.

表1　不同负荷下CFB锅炉采用不同煤种时床温的传递函数模型参数

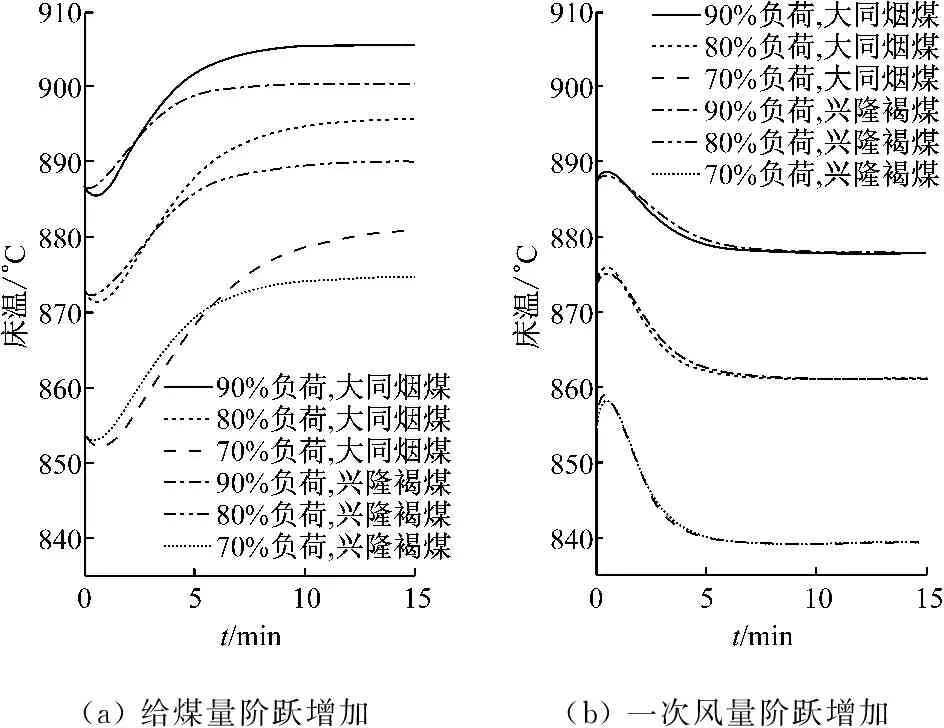
(a)给煤量阶跃增加(b)一次风量阶跃增加

图1不同工况下CFB锅炉床温的阶跃响应曲线

Fig.1Step response of bed temperature of CFB boiler at different operating points

从图1可以看出，给煤量阶跃增加时，床温先下降，再逐渐上升到新的平衡状态.一次风量阶跃增加时，床温在短时间内先上升，再逐渐下降到新的平衡状态.床温在初始阶段具有逆响应特性，这给控制系统的设计带来困难.而且负荷的变化会显著影响CFB锅炉床温的动态特性.如低负荷时给煤量-床温的静态增益高于高负荷时的静态增益，并且低负荷时床温的动态响应时间比高负荷时稍长.低负荷时一次风量-床温的静态增益高于高负荷时的静态增益，并且低负荷时床温的动态响应时间比高负荷时要短.此外，煤质的变化也会影响床温的动态特性,如低位发热量较高的大同烟煤对应的给煤量-床温静态增益要高于低位发热量较低的兴隆褐煤对应的给煤量-床温静态增益.

2基于SOPDT模型的预估滑模控制方案

图2　基于SOPDT模型的预估滑模控制方案

2.1基于SOPDT模型的预估模型

工程上,通常用一阶加纯滞后(First-order Plus Dead-time，FOPDT)模型或二阶加纯滞后(SOPDT)模型描述被控对象的动态特性.相比于FOPDT模型，SOPDT模型具有更广泛的适用性，采用SOPDT模型近似逼近高阶对象得到的精度通常很高，足以满足生产过程中控制器设计对模型精度的要求，因此，笔者基于SOPDT模型设计滑模控制器.

假定在标称工况下辨识得到被控对象的SOPDT传递函数模型为：

(4)式中：K、T、ζ和τ分别为稳态增益、自然振荡周期、阻尼系数和过程的迟延时间；a1=1/T2，a2=2ζ/T，b1=K/T2.

对应的二阶微分方程为：

(5)

式中：u和ym分别表示标称模型的输入和输出.

将迟延时间τ从式(5)中移除，可得无迟延预估模型：

(6)

式中：yf(t)为利用无迟延模型得到的超前一个迟延时间段τ(即t+τ时刻)的输出估计值.

为了能够在有建模误差和未测干扰时提高预测的准确性，实际应用时可通过式(7)对过程输出预测值进行修正.

(7)

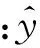
2.2滑模控制器设计

一般的热工调节问题，要求被控对象的被控变量y(t)能够跟踪其期望的设定值信号r(t)，并能抑制各种干扰对系统输出的影响.因而，控制器设计的目的是使实际输出能够跟踪其设定值或维持在其设定值附近，使得误差趋近于零.

考虑一个不确定模型：

(8)

式中：d(t)为被控过程总的不确定性，包括参数不确定性和外部干扰.假定d(t)是有界的，|d(t)|≤ρ，ρ>0为不确定性的上界值.

首先，选择滑模函数(也称切换函数)为：

(9)

式中：e(t)=r(t)-yf(t)；λ为滑模系数.

因滑模面上s(t)=0，则由式(9)可得到滑模运动方程：

(10)

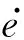
基于滑模函数式(9)，针对不确定模型式(8)，可设计如下的滑模控制律：

(11)

其中，

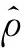
滑模控制器设计一般需要知道不确定性的上界，但这些上界值实际上难以得到.为此，使用自适应技术来对不确定性上界进行估计，式(12)为不确定性上界估计值的自适应更新律.

(12)

式中：γ为自适应增益，γ>0.

当选用式(9)所示的滑模函数，将滑模控制律式(11)作用于不确定模型式(8)时，闭环系统能够渐进稳定.证明如下：

选择如下的非负李亚普诺夫Lyapunov函数

(13)

对滑模函数式(9)求微分并代入控制律式(11)，可得：

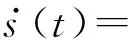
(14)

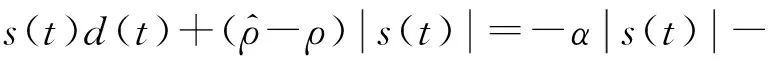
(15)

2.3预估滑模控制方案的具体实施

笔者所提出的预估滑模控制方案本质上是一种利用不确定性边界的方法，闭环系统的性能由滑模函数决定.为了减少不必要的切换，避免产生抖振现象，实际应用时可用式(16)中的饱和函数sat替换式(11)中的符号函数sign.

(16)

式中：β表示边界层的宽度，β>0.

(17)

式中：αr为滤波系数，0<αr≤1；Ts为采样周期；参考输出yr(t)的初值yr(0)=y(0).

(18)

其中滑模函数

若被控对象具有参数不确定性和外部干扰，可以用下面的不确定模型表示：

(b1+Δb1)u(t-τ)+w(t)

(19)

式中：Δa1、Δa2和Δb1为系统参数不确定部分；w(t)为外部干扰.

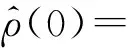
|w(0)|

(20)

预估滑模控制器包含4个参数：α、β、λ和γ.α与闭环系统的性能相关，α越大，系统的响应越快，但此时控制作用较大.引入参数β是为了消除输入的抖振，通常β的选择是为了权衡控制精度和输入抖振程度.滑模函数中系数λ的取值会影响滑模运动轨迹，从而进一步影响系统的性能.自适应增益γ用于调整不确定性上界估计值的收敛速率.

2.4推广应用于非最小相位过程

对于非最小相位系统，其阶跃响应会出现负调，这对实施控制非常不利，如何在克服负调的同时抑制超调并缩短过渡时间是一个控制难题.笔者通过对辨识模型进行简单处理，将预估滑模控制方案直接推广应用于控制非最小相位过程.

假定对非最小相位过程进行辨识后得到如下SOPDT模型：

(21)

式中：b2/b1<0，因为非最小相位过程具有不稳定零点(即右半复平面零点).

非最小相位模型式(21)可近似转化为标准的无零点SOPDT模型：

(22)

根据式(21)中的分子部分b2s+b1，利用指数函数的一阶泰勒级数式(23)可近似得到等价迟延时间τeq≈-b2/b1.

(23)

因此，前面基于无零点SOPDT模型的预估滑模控制方法就可以直接处理非最小相位过程.虽然等价迟延时间方法会带来额外的建模误差，但这种增加的模型不确定性可以很容易地通过适当提高不确定性上界初始估计值和自适应技术来解决.

3CFB锅炉床温的预估滑模控制仿真研究

将所提出的预估滑模控制(Predictive Sliding Mode Control，PSMC)方法应用于CFB锅炉给煤量-床温通道的床温控制.为便于对比，文中利用另外2种具有较强鲁棒性的控制方法，即Camacho等[9]提出的基于内模的滑模控制方法(IM-SMCr)和Morari等[10]提出的基于内模思想整定的PID控制方法(IMC-PID)，也分别设计了相应的床温控制系统.表2列出了3种不同控制系统在90%负荷下采用大同烟煤的给煤量-床温模型作为标称模型而设计的控制器参数取值.

表2　3种不同控制系统的控制器参数

试验1：床温设定值跟踪.

假定90%负荷下床温设定值从887 ℃阶跃升高5 K，图3所示为应用不同控制方法时床温响应曲线和控制器输出(即给煤变化量)曲线.从图3可以看出，采用PSMC方法能获得更小的超调量和更短的调节时间，控制效果明显优于IM-SMCr方法和IMC-PID方法.在控制器参数不变的情况下，图4给出了在80%负荷下床温设定值从873 ℃阶跃升高5 K时的控制效果，由于负荷变化后床温模型与实际对象特性不匹配，3种控制系统的性能均有所下降，但PSMC方法的性能仍优于其他方法.

试验2：抗阶跃外扰.

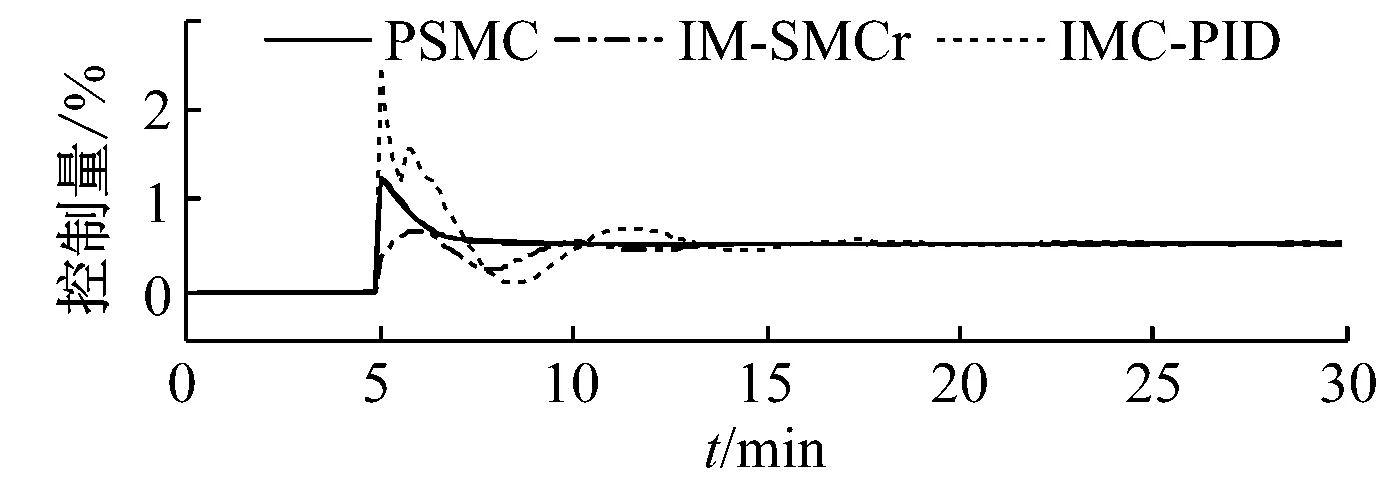
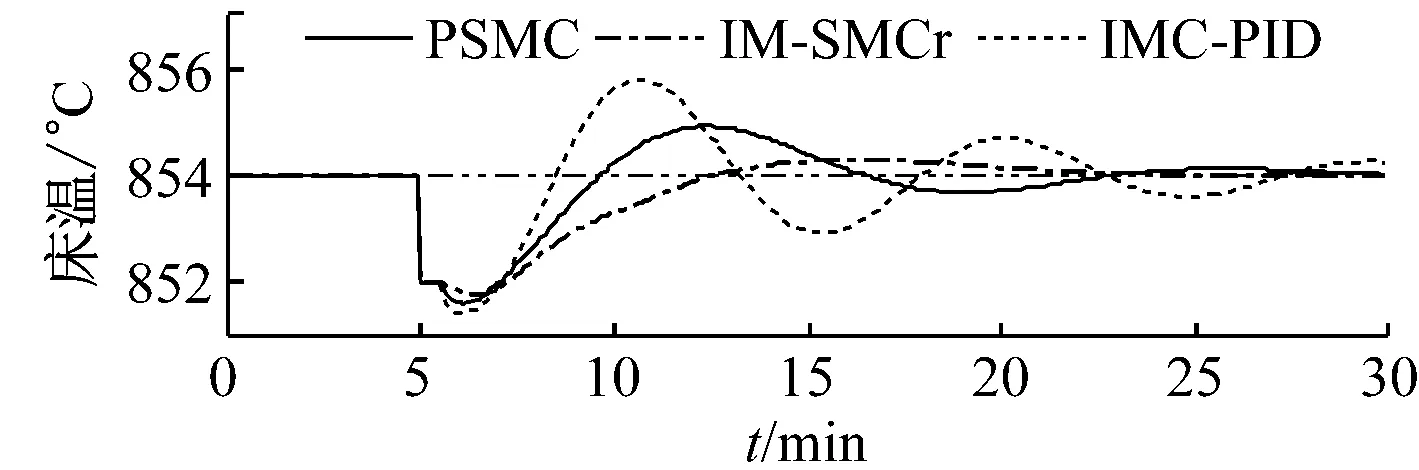
假设由于一次风、二次风配比、石灰石量、排渣量或返料量等因素的影响导致床温在t=5 min时偏离其设定值2 K.图5和图6分别给出了90%和70%负荷下不同床温控制系统的抗外扰效果.由图5和图6可知，在模型与对象匹配的情况下，PSMC方法具有很强的抗外扰能力，能在短时间内抑制住床温的波动且动态偏差小；在模型与对象不匹配的情况下，虽然控制性能有所下降，但仍能进行有效控制.

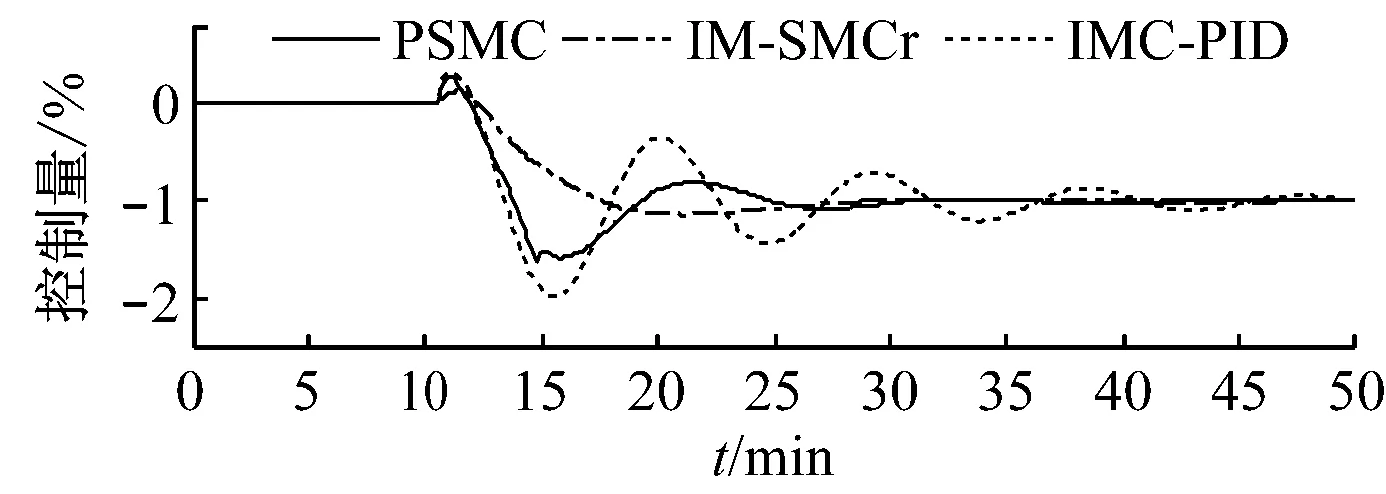
试验3：抗给煤量扰动.

(a)

(b)

(a)

(b)

(a)

(b)

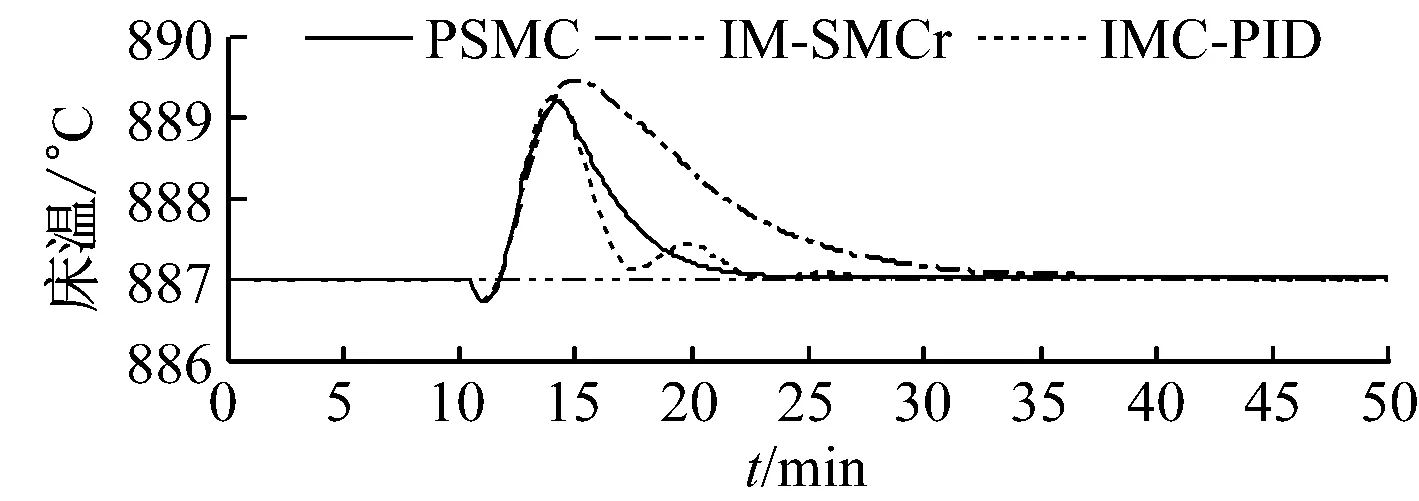
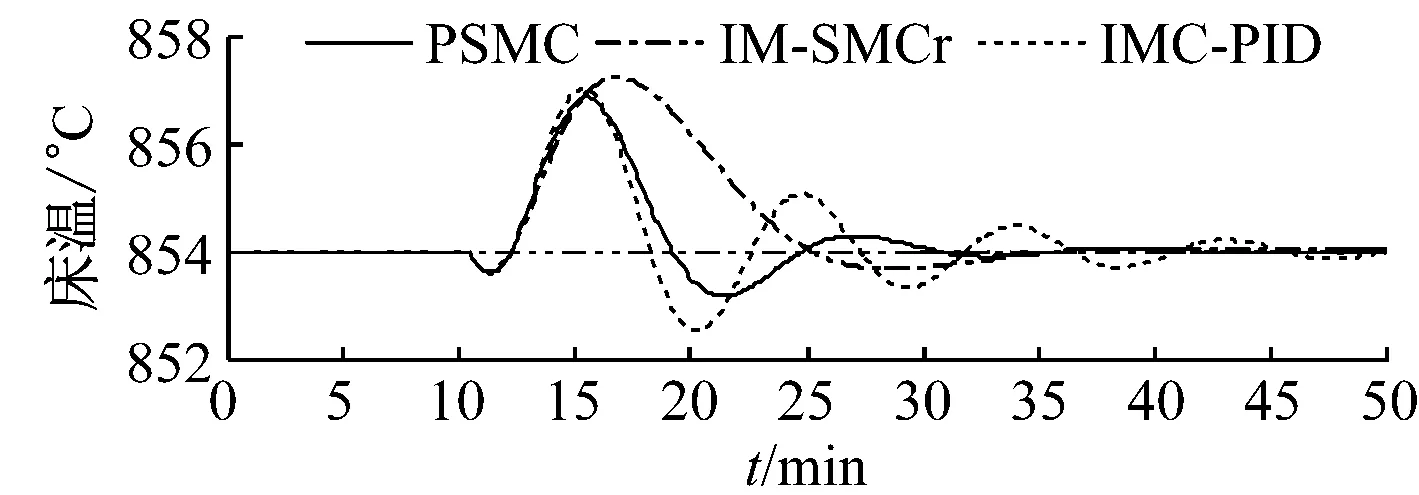
假定给煤量发生自发性扰动，在t=10 min时突然增加0.5%.图7和图8分别给出了90%和70%负荷下床温控制系统的抗内扰性能.由图7和图8可知，在模型与对象匹配的情况下，PSMC方法具有很强的抗内扰能力，能在很短时间内抑制床温的波动且动态偏差小；在模型与对象不匹配的情况下，虽然控制性能有所下降，但仍能进行有效控制.

试验4：抗煤质扰动.

(a)

(b)

(a)

(b)

(a)

(b)

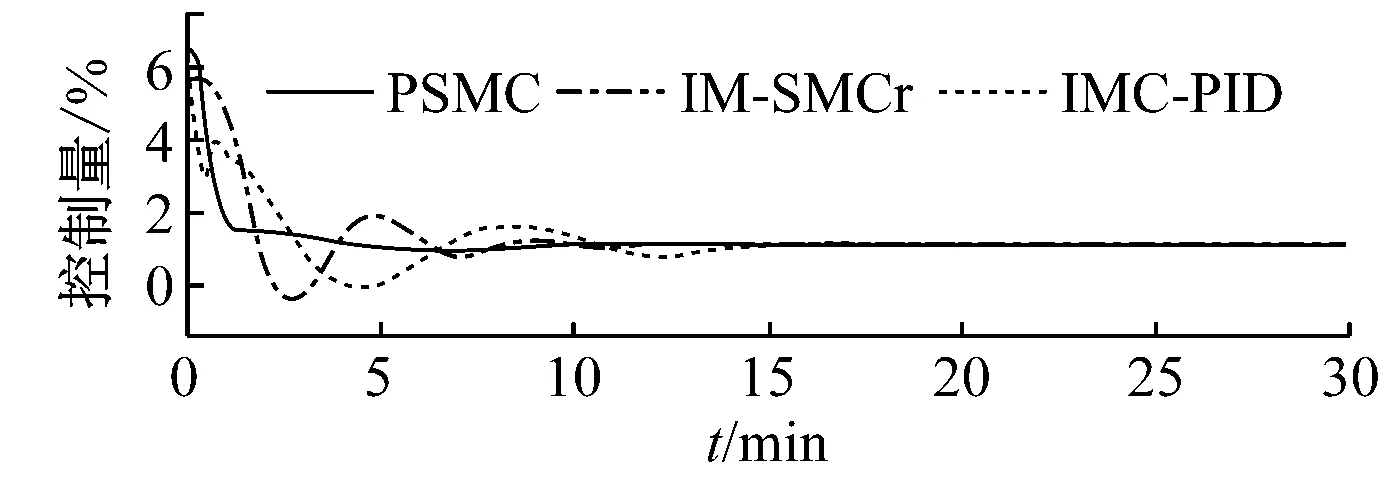
假定90%负荷下床温稳定在其相对设定值1上，对应控制量相对值为0.268 8，在t=5 min时煤种由原来的大同烟煤变化为阳山无烟煤，煤质变化导致床温偏离其设定值.3种控制系统的控制效果如图9所示，在PSMC方法的控制作用下床温能够快速地恢复到原来的设定值.图10给出了70%负荷下煤种发生变化时的控制效果，由于70%负荷下采用阳山无烟煤时床温动态特性与90%负荷下采用大同烟煤时的特性差异较大，因而3种控制系统的控制效果均有所下降，但总体上PSMC方法的性能仍优于其他2种控制方法.

通过上述4个仿真实验可以看出，笔者提出的PSMC方法具有良好的设定值跟踪性能和抗干扰能力以及强鲁棒性.

(a)

(b)

(a)

(b)

4结论

针对循环流化床锅炉床温等具有大惯性、大滞后的复杂热工对象因负荷、煤种、环境条件改变以及模型简化等带来的不确定性问题，设计了一种简单而新颖的基于SOPDT模型的预估滑模控制方案.它基于辨识得到的标称SOPDT模型，构建无迟延预估模型用于过程输出预测，并通过合理设计滑模函数和不确定上界自适应估计的滑模控制律，使得具有不确定性的闭环系统能在任何外扰下保持渐进稳定.该预估滑模控制方法还可扩展应用于具有逆反应过程的非最小相位系统.针对循环流化床锅炉床温对象设计了相应的预估滑模控制系统，仿真结果表明：采用PSMC方法的效果明显优于基于内模原理设计的一般滑模控制器和PID控制器，具有良好的负荷适应性及抗各种不确定性和干扰的能力.

参考文献：

[1]于希宁，王慧，王东风，等．模糊控制在循环流化床锅炉床温控制中的应用[J]．华北电力大学学报，2005，32(3)：43-46．

YU Xining, WANG Hui, WANG Dongfeng,etal. Application of fuzzy-PID control algorithm in bed temperature control of circulating fluidized bed boiler[J]. Journal of North China Electric Power University, 2005, 32(3): 43-46.

[2]马宝萍，司凤琪，徐治皋，等．基于遗传算法的循环流化床锅炉床温模糊控制系统[J]．中国电机工程学报， 2001，21(11)：69-73．

MA Baoping, SI Fengqi, XU Zhigao,etal. Genetic-based fuzzy bed temperature control system of circulating fluidized bed boiler[J]. Proceedings of the CSEE, 2001, 21(11): 69-73.

[3]林永君，管志敏，彭钢，等．基于自抗扰控制的循环流化床锅炉床温系统的研究[J]．热能动力工程，2010，25(5)：514-516.

LIN Yongjun, GUAN Zhimin, PENG Gang,etal. Study of the bed temperature system for a circulating fluidized bed boiler based on a self disturbance-resistant control[J]. Journal of Engineering for Thermal Energy & Power, 2010, 25(5): 514-516.

[4]张媛媛．神经网络预测控制在循环流化床锅炉床温系统的应用[J]．电力学报，2009，24(2)：121-124．

ZHANG Yuanyuan. NN predictive control of CFB bed temperature system[J]. Journal of Electric Power, 2009, 24(2): 121-124.

[5]董湛波，向文国，王新．基于多模型的循环流化床锅炉床温预测控制[J]．动力工程学报，2011，31(3)：181-186．

DONG Zhanbo, XIANG Wenguo, WANG Xin. Predictive control on bed temperature of CFB boilers based on multiple models[J]．Journal of Chinese Society of Power Engineering, 2011, 31(3): 181-186.

[6]刘金昆，孙富春．滑模变结构控制理论及其算法研究与进展[J]．控制理论与应用，2007，24(3)：407-418．

LIU Jinkun, SUN Fuchun. Research and development on theory and algorithms of sliding mode control[J]. Control Theory & Applications, 2007, 24(3): 407-418.

[7]陈志梅，贞艳，张井岗．滑模变结构控制理论及应用[M]．北京：电子工业出版社，2012．

[8]仇韬．循环流化床锅炉在负荷和煤质波动下的控制问题研究[D]．北京：清华大学，2007．

[9]CAMACHO O, ROJAS R, GARCíA-GABíN W. Some long time delay sliding mode control approaches[J]. ISA Transactions, 2007, 46(1): 95-101.

[10]MORARI M, ZAFIRIOU E. Robust process control[M]. New Jersey, USA:Prentice-Hall, Englewood Cliffs, 1989.

Predictive Sliding Mode Control on Bed Temperature of CFB Boilers

ZHUHongxia1,2,SHENJiong1,LIYiguo1

(1. School of Energy and Environment, Southeast University, Nanjing 210096, China; 2. School of Energy and Power Engineering, Nanjing Institute of Technology, Nanjing 211167, China)

Abstract：To tackle the uncertainties caused by variations of load, coal and environmental conditions as well as by model simplification, a predictive sliding mode control strategy, which is easily understandable and applicable in practice, was proposed for the thermal processes with large inertia or time delay. Firstly, a predictive model without output delay was established to estimate the process output by using a second-order plus dead-time (SOPDT) model obtained in nominal case. Secondly, a reasonable sliding function and a sliding mode control law with adaptively estimated uncertain upper bound were designed to asymptotically stabilize the closed-loop system with uncertainties and disturbances. On the basis above, numerical simulations were conducted on bed temperature of a circulating fluidized bed (CFB) boiler. Results show that the control strategy proposed is fast in bed temperature regulation with small overshoot and strong anti-disturbance capability.

Key words：predictive sliding mode control; SOPDT model; uncertainty; circulating fluidized bed; bed temperature

收稿日期：2015-06-29

基金项目：国家自然科学基金资助项目(51476027)； 教育部高等学校博士学科点专项科研基金资助项目(20130092110061)； 南京工程学院青年基金资助项目(QKJA201303)

作者简介：朱红霞(1980-)，女，江苏南通人，副教授，博士研究生，研究方向为先进控制理论在热工过程中的应用.

文章编号：1674-7607(2016)05-0365-07中图分类号：P273

文献标志码：A学科分类号：470.20

电话(Tel．)：13512535256；E-mail：zhxia@njit.edu.cn.