作用于椭圆沉箱上的非线性波浪力研究
2016-07-22胡伟纪师明任效忠王琪马玉祥
胡伟,纪师明,任效忠,王琪,马玉祥
(1.大连海洋大学基建管理处,辽宁大连116023;2.中交一航局第三工程有限公司,辽宁大连116083;3.大连九成市政设计有限公司,辽宁大连116000;4.大连理工大学运载工程与力学学部船舶工程学院,辽宁大连116024;5.大连理工大学海岸和近海工程国家重点实验室,辽宁大连116024)
作用于椭圆沉箱上的非线性波浪力研究
胡伟1,纪师明2,任效忠3,王琪4,马玉祥5
(1.大连海洋大学基建管理处,辽宁大连116023;2.中交一航局第三工程有限公司,辽宁大连116083;3.大连九成市政设计有限公司,辽宁大连116000;4.大连理工大学运载工程与力学学部船舶工程学院,辽宁大连116024;5.大连理工大学海岸和近海工程国家重点实验室,辽宁大连116024)
摘要:为深入研究椭圆沉箱的水动力特性,建立了非线性波浪与结构物相互作用的三维时域数值计算模型,该模型中N-S方程的求解基于有限差分法,采用VOF方法追踪流体自由表面,使用部分单元体方法处理椭圆沉箱结构物的曲面边界,用计算圆沉箱波浪力对该模型进行了验证,并将该模型应用于相对波高(H/d)、相对波长(kD)和相对长宽比(B/D)对椭圆沉箱波浪力的影响研究。结果表明:相对波高对椭圆沉箱波浪力有重要影响,其值越大波浪非线性的影响越明显;与沉箱无量纲正向波浪力相比,相对长宽比对无量纲横向波浪力影响更大。研究表明,本研究中建立的数值模型可应用于椭圆沉箱波浪力的计算,但实际设计中需依据建设地点的风浪特征与掩护条件,确定合适的沉箱相对长宽比,以保证结构足够的安全系数。
关键词:椭圆沉箱;波浪力;VOF方法;部分单元体
椭圆沉箱是一种应用于开敞式深水码头的新型结构型式,该结构由三部分组成,沉箱的前后两部分是半圆形断面,中间部分是矩形断面。为了克服两排圆沉箱的不均匀沉降,专业人员设计了椭圆沉箱结构,避免了采用大型圆沉箱对应强浪方向断面大、波浪壅高的不利影响。椭圆沉箱重力墩首次在大连矿石码头二期工程中被实施应用[1],解决了大型圆沉箱方案码头面高程较高的难题,降低了建设成本,并方便运营作业。之后,椭圆沉箱在青岛港董家口港区40万t矿石码头[2]建设中作为主体结构再次得到应用。椭圆沉箱与传统小型圆沉箱结构方案相比,减少了50%沉箱数量,且沉箱上部不搭设联结前后沉箱间的联系梁,上部预制安装构件数量不仅大大减少,而且码头整体性更好。椭圆沉箱在使用性能、安全性能和经济效益方面均有突出优势,具有广泛的推广应用前景。
椭圆沉箱结构作为新型深水重力码头结构型式,需深入研究其水动力特性。任效忠等[3-4]进行了椭圆沉箱波浪力的试验研究工作,但试验仅考虑了沉箱相对长宽比B/D为0.63的模型。任效忠等[5]还利用二维源分布法研究了波浪对椭圆沉箱作用的线性波浪力。然而,对于较大的波浪,由线性理论计算的椭圆沉箱波浪力比试验结果小很多,因此,需要建立非线性时域数值模型。本研究中,建立了非线性波浪与结构物相互作用的三维时域数值计算模型,并将该数值模型应用于相对波高、相对波长和相对长宽比对椭圆沉箱波浪力的影响研究中。模型中N-S方程的求解基于有限差分法,采用VOF方法追踪流体自由表面[6-8],采用部分单元体法处理椭圆沉箱的边界,较好地满足了该模型的计算效率与计算精度要求。
1 数值模型
1.1控制方程
基于流体为粘性不可压缩的基础假设,流体控制方程采用连续性方程和N-S方程。流体体积函数F用于追踪流体自由面,单元体内流体占有的体积比率用F表示,流体控制方程为
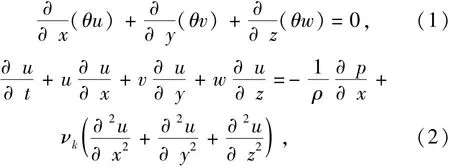
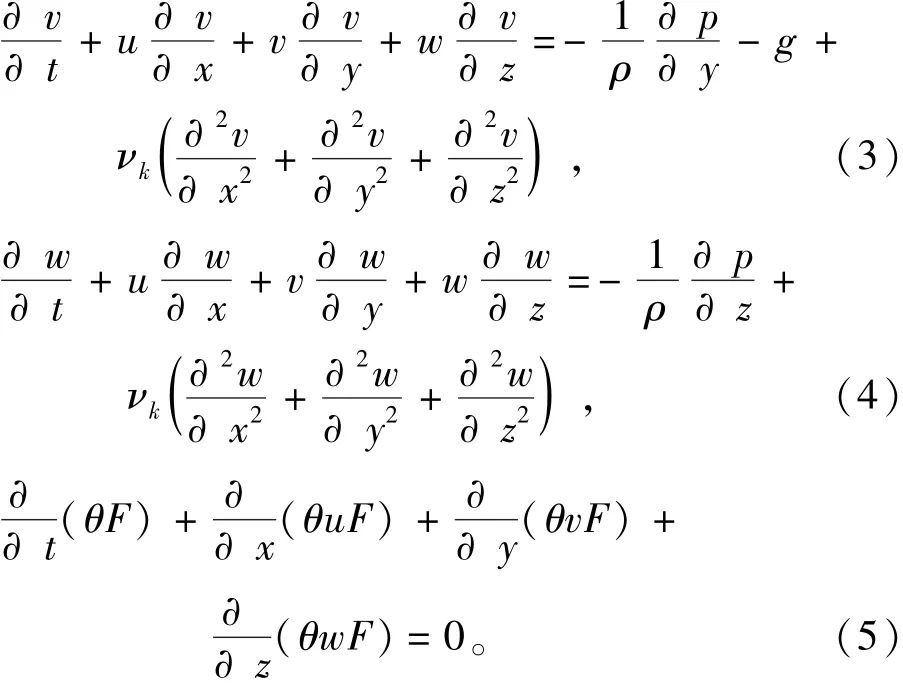
其中:u、v、w分别为x、y、z轴的速度分量;t为时间参数;g为重力加速度;ρ为流体密度;p为压力;νk为运动粘性系数;θ为部分单元体参数,θ∈[0,1]。计算参数:ρ=1000 kg/m3,g=9.80 m/s2,νk=1.002×10-6m2/s。
单元体中的F值定义为单元体被流体占有的体积比率,即F=1表示充满流体,F=0表示无流体,0<F<1表示该单元体未充满流体,一种情形是单元体与自由表面相交的自由表面单元体,另一种情形是含有比单元体尺度小的空气泡。
1.2数值计算方法
1.2.1有限差分方法 将交错网格应用于有限差分求解控制方程,如图1所示。参数p、F位于单元体的中心。速度分量u定义在单元体的右侧面中心,记为ui+1/2,j,k;v定义在单元体顶面的中心,记为vi,j+1/2,k;w定义在单元体前面的中心,记为wi,j,k+1/2。ARi,j,k、ATi,j,k和AFi,j,k表示3个面非边界部分面积的比率 (分别对应单元体右侧面、顶面和前侧面);而VCi,j,k表示单元体非边界部分体积的比率。N-S方程离散中时间项的处理采用时间向前差分格式,粘性项基于二阶中心差分格式;用基于迎风差分与二阶中心差分的混合差分格式处理对流项。
本研究中,应用SOLA-VOF算法让每个控制体满足差分方程。每一计算时间步长,求解出各个控制体的速度场和压力。用前一时刻计算的流场结果代入显式格式的动量方程,得到当前时刻的流场近似值。为满足连续方程,充满流体的每个计算单元体的压力和速度必须进行修正。通过反复迭代法修正每一个单元体的压力,内部流体单元体修正后使连续方程达到预设精度要求。表面单元体首先满足自由表面的动力边界条件,其压力通过自由表面处压力和内部流体单元压力线性插值求解得到。
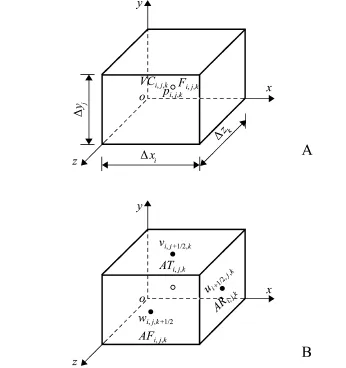
图1 单元体结构示意图Fig.1 Sketch of a staggered cell
每个计算流体单元经过上述插值过程得到速度场与压力,然后通过流体体积函数F计算得到新时刻的流体分布。流体体积函数F是阶梯函数,自由面变化由单元体流体通量的计算确定,单元体边界面上的流体通量采用施主与受主单元体模型计算,最后计算得到F函数。
1.2.2边界条件 本研究中,三维数值波浪水池如图2所示,L为水池长度 (m),B为水池宽度(m),d为水深 (m),L1为水池有效区域长度(m),L2为速度衰减区域长度 (m)。
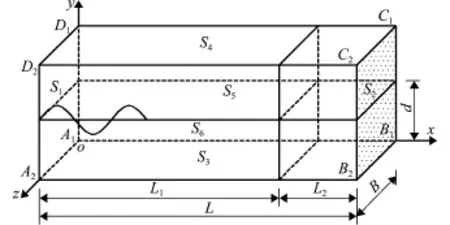
图2 数值波浪水池示意图Fig.2 Sketch of a numerical wave tank
在水池的左侧 (S1=SA1A2D2D1)设置造波推板。依据可吸收造波理论,造波中产生行进波的同时还产生附加波动将水池反射抵消,以消除反射波对计算的影响,附加波动与反射波幅值相等,相位相反[9-10]。基于椭余波理论,造波推板速度表达式为
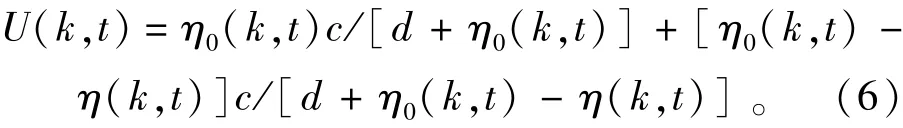
其中:η(k,t)为第kth块造波板前的实际波面;η0(k,t)为依据椭余波理论需要的波面;d为水深;c为椭余波波速。
采用数值衰减与开边界两种处理方法,减小波浪反射对数值计算的干扰。与波浪水池右端(S2= SB1B2C2C1)相邻的L2区域是数值衰减区域,L2区域中垂向速度的衰减系数为
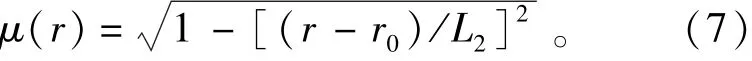
其中:r0为数值衰减的起点;L2为数值衰减区的长度。数值衰减区中的垂向速度为由控制方程得到的垂向速度乘以衰减系数。为进一步减小反射干扰,依据Sommerfeld辐射条件,右侧开边界的出流速度可以表示为

其中:k为波数;ω为角频率;η为开边界处的自由面。
椭圆沉箱边界由部分单元体方法处理。波浪水池的侧面边界(S5=SA1B1C1D1、S6=SA2B2C2D2)和底面边界(S3=SA1A2B2B1)设置为自由滑移直墙边界。在数值计算中,自由滑移直墙边界的法向速度和切向速度的法向导数均设为0。
2 数值模型的验证
2.1数值波浪水池的稳定性
本研究中,对数值波浪水池的主要指标数值耗散、计算稳定性和造波重复性均进行了验证。波高H=1.0~4.0 m,周期T=8.0~13.0 s,水深d=20 m。水池总长L=800 m,其中水池有效区域长L1= 600 m,水池宽度B=260 m。单元体网格尺度为Δx=2 m、Δy=3 m和Δz=2 m。表1列出了沿水池距造波板一倍波长 (λ)、两倍波长 (2λ)、三倍波长 (3λ)、四倍波长 (4λ)位置处的5个波的平均波高。图3为位于两倍波长处的典型波面历时曲线。图4为数值波浪水池的瞬时波面。从数值计算结果可知,数值波浪水池的波浪均匀性和重复性均比较好,故数值波浪水池能满足计算所需。
2.2波浪力计算
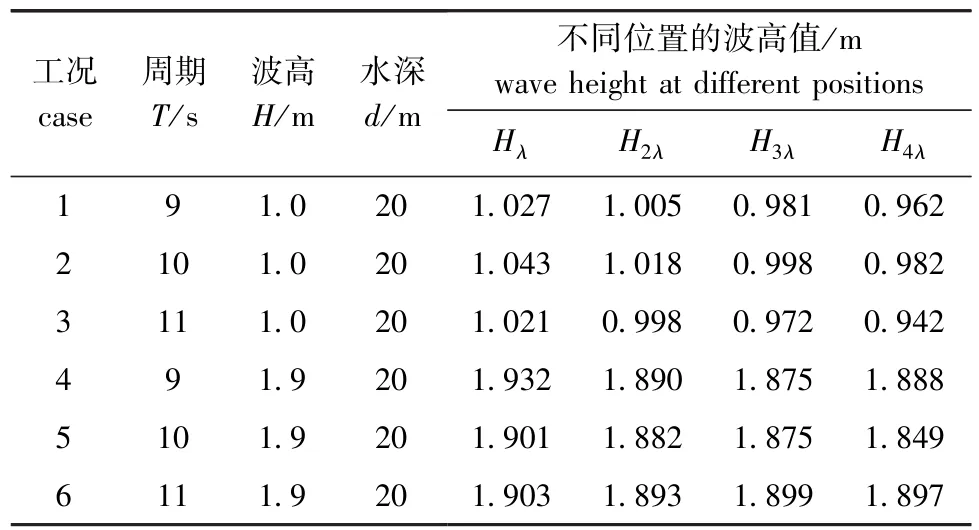
表1 数值水池中不同位置的波高值Tab.1 Wave height at different positions in a tank
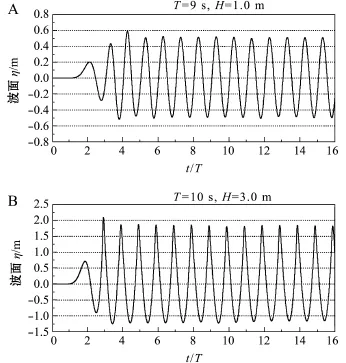
图3 数值波浪水池波面历时曲线 (x=2λ)Fig.3 Time history of wave surface at location(x=2λ)
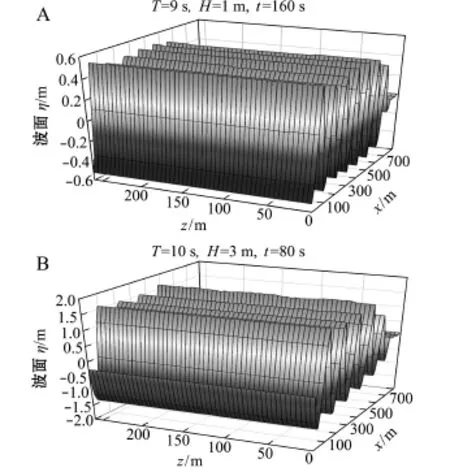
图4 数值波浪水池波面分布示意图Fig.4 Instantaneous wave surface in a tank
在弱非线性条件下,用本研究中建立的数值模型计算直立圆柱水平波浪力,并将数值计算结果与波浪绕射理论[11-14]的解析结果进行对比。计算时,设水深d=20 m,波高H=1.9 m,波浪周期T= 8.0~13.0 s,圆柱半径=10 m。直立圆柱的曲面边界采用部分单元体处理,边界周围的单元节点平面坐标如图5所示。直立圆柱水平波浪力的数值计算结果及比较见表2,数值计算结果比解析结果大7%~11%。
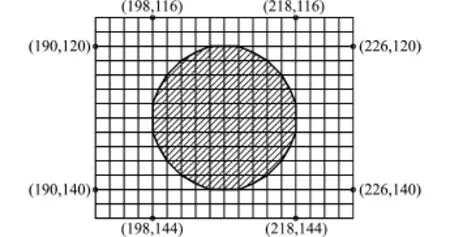
图5 直立圆柱网格示意图Fig.5 Sketch of cells on a vertical circular cylinder
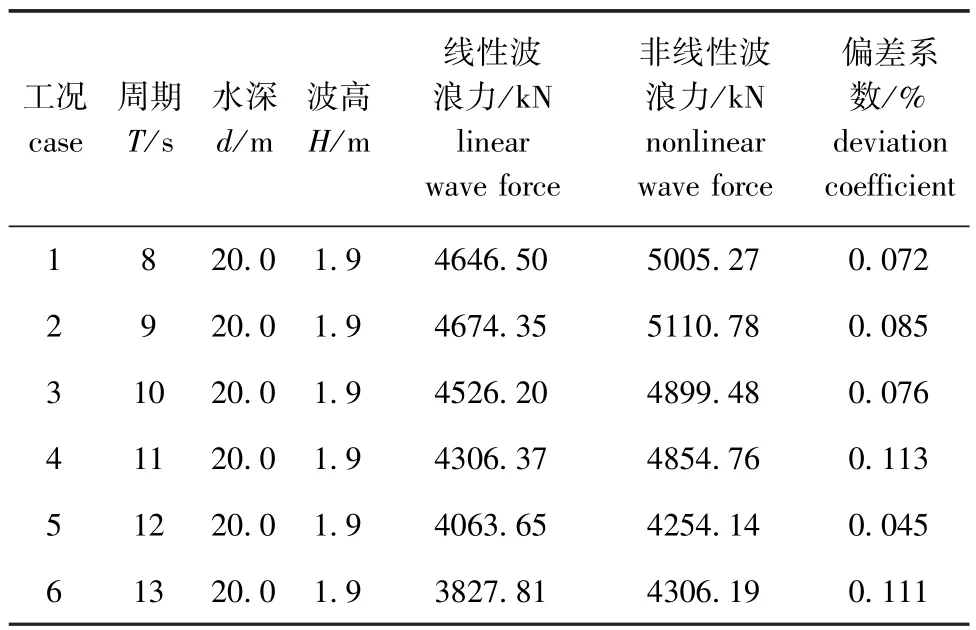
表2 直立圆柱水平波浪力与解析解的比较Tab.2 Comparison of the horizontal wave force on a vertical circular cylinder with analytical solution
3 椭圆沉箱结构波浪力的计算
椭圆沉箱结构示意图见图6,由3部分组成。沉箱的前部分和后部分为半圆形断面,半圆直径为D;沉箱的中间部分为矩形断面,矩形长度为B。
计算参数中:设H=1.0~4.0 m,T=8.0~13.0 s,d=20 m,相对波长kD=0.7~1.5;椭圆沉箱半圆形断面直径为20 m,相对长宽比B/D= 0~0.8;入射波角度α=0°和α=45°;迭代过程收敛精度ε设为0.005。采用部分单元体法处理椭圆沉箱曲面边界,椭圆沉箱边界周围的单元节点平面坐标如图7所示 (单位为m)。计算设置初始时间步长Δt=0.04 s,计算过程中时间步长能实现自动调整,以符合Courant条件和扩散稳定条件。
通过本研究中建立的数值模型计算得到椭圆沉箱的椭余波波浪力,并进行无量纲化处理。无量纲正向波浪力和无量纲横向波浪力的表达式为
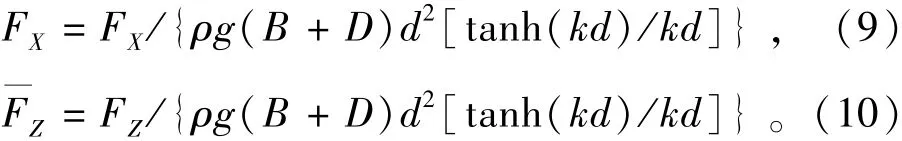
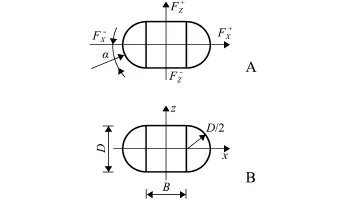
图6 椭圆沉箱结构示意图Fig.6 Sketch of an ellipse caisson
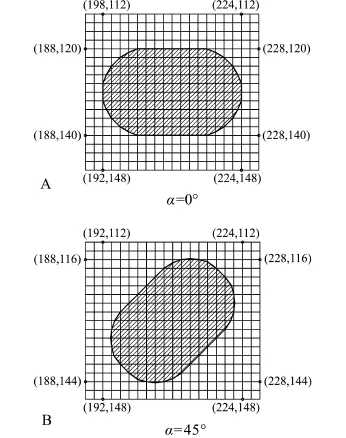
图7 圆沉箱计算网格示意图 (B/D=0.6)Fig.7 Sketch of the cells on ellipse caisson(B/D=0.6)
将B/D=0.6及不同相对波高下椭圆沉箱波浪力的数值计算结果和基于二维源分布法的线性波浪力结果进行比较,结果见图8-A、B。图8中,实心图例和实线代表数值计算结果,空心图例和虚线代表线性结果。比较结果显示:数值计算的无量纲正向波浪力和无量纲横向波浪力均比线性结果大;随着相对波高H/d的增大,非线性特征的影响在计算结果中体现的越明显,说明H/d对椭圆沉箱波浪力有重要影响。H/d越大,用数值模型计算的无量纲波浪力越大,越不容忽视波浪非线性的影响。
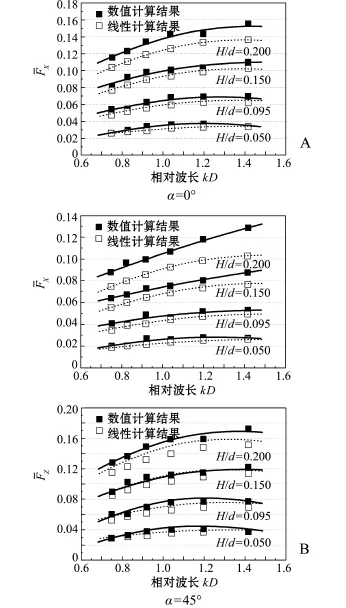
图8 椭圆沉箱非线性和线性波浪力计算结果的对比(B/D=0.6)Fig.8 Comparison of nonlinear and linear wave forces on the quasi-ellipse caisson(B/D=0.6)
图9-A、B分别为波浪入射角度为0°和45°时,不同相对长宽比下椭圆沉箱波浪力的数值计算结果,其中,H/d=0.15,B/D=0~0.8。随着相对波长kD的增大,无量纲波浪力和呈现增大趋势;随着B/D的增大,减小,而呈增大趋势,相对,B/D对有更大影响。
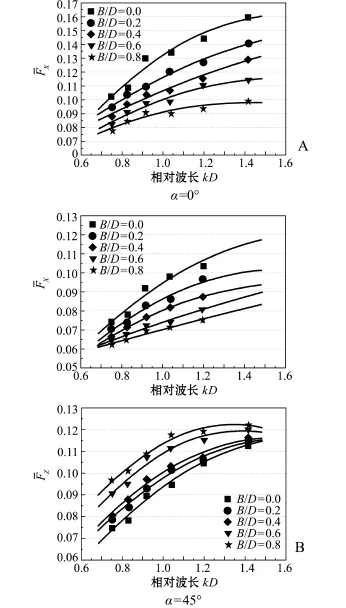
图9 不同相对长宽比与无量纲椭圆沉箱波浪力的关系(H/d=0.150)Fig.9 Nondimensional wave force of the quasi-ellipse caisson versus kD at different relative lengthwidth ratio(H/d=0.150)
因此,实际设计中选择沉箱B/D时,应依据建设地点的风浪特征与掩护条件,确定合适的沉箱B/D,在保证结构足够安全的同时,充分发挥椭圆沉箱的优势。在同样码头建设宽度条件下,减小沉箱正向迎浪面积,可增大沉箱间的间距,削弱沉箱间的相互干扰,同时也缩减了建设工程量与工程投资。
4 结论
(1)本研究中基于有限差分法,并结合VOF方法和部分单元体方法,建立了非线性波浪与结构物相互作用的三维时域数值计算模型,用该数值模型模拟了椭圆沉箱的非线性波浪力,并得到椭圆沉箱波浪力的非线性特征。对于大型结构椭圆沉箱,波浪力的非线性特征随相对波高的逐渐增大而更加明显,波浪非线性的影响不容忽视。
(2)随着沉箱相对长宽比的增大,无量纲正向波浪力逐渐减小,而无量纲横向波浪力逐渐增大。与无量纲正向波浪力相比,沉箱相对长宽比对无量纲横向波浪力影响更大。波浪斜向入射(45°)结果显示,当沉箱相对长宽比为0.6和0.8时,无量纲横向波浪力明显大于无量纲正向波浪力。
(3)选用合适的沉箱相对长宽比是设计中必须重视的问题。对掩护条件好、大风向和大浪向常年集中的海域,适合采用相对长宽比较大的椭圆沉箱,充分发挥椭圆沉箱的优势;而掩护条件差、复杂多变的海域宜选择相对长宽比较小的椭圆沉箱,以增强沉箱的抗倾覆能力,保证结构使用安全。
参考文献:
[1]白景涛,胡家顺.椭圆沉箱墩式码头新结构的研究与设计[J].水运工程,2006(11):25-30.
[2]张志明,胡家顺,郑小楠,等.青岛港董家口港区40万t矿石码头设计关键技术[J].水运工程,2011,457(9):61-67,127.
[3]Ren Xiaozhong,Wang Yongxue,Wang Guoyu.The wave force on the multiple quasi-ellipse caissons[C]//Proceedings of the Fourth International Conference on Asian and Pacific Coasts.Nanjing China:APAC,2007:201-208.
[4]任效忠,王永学,王国玉.准椭圆沉箱群墩结构波浪力试验研究[J].大连理工大学学报,2009,49(6):944-950.
[5]任效忠,王永学,王国玉.不规则波作用下准椭圆沉箱单墩的波浪荷载[J].船海工程,2009,38(1):85-89.
[6]Hirt C W,Nichols B D.Volume of Fluid(VOF)method for the dynamics of free boundaries[J].Journal of Computational Physics,1981,39(1):201-225.
[7]万德成,缪国平.数值模拟波浪翻越直立方柱[J].水动力学研究与进展,1998,13(3):363-370.
[8]齐鹏.近岸波浪对结构物作用耦合数值模型及其工程应用[D].大连:大连理工大学,2001.
[9]李晓磊,栾曙光,陈勇,等.立方体人工鱼礁背涡流的三维涡结构[J].大连海洋大学学报,2012,27(6):572-577.
[10]Wang Yongxue,Zang Jun,Qiu Dahong.Numerical model of cnoidal wave flume[J].China Ocean Engineering,1999,13(4):391-398.
[11]王永学,Su T C.圆柱容器液体晃动问题的数值计算[J].空气动力学学报,1991,9(1):112-119.
[12]Maccamy R C,Fuchs R A.Wave forces on piles:a diffraction theory[R].Technical Memorandum No.69,California:US Beach E-rosion Board,1954.
[13]桂劲松,温志超,毕恩凯,等.渔港建设标准中码头岸线长度的确定[J].大连海洋大学学报,2015,30(5):558-562.
[14]李玉成,滕斌.波浪对海上建筑物的作用[M].2版.北京:海洋出版社,2002.
中图分类号:U656.22
文献标志码:A
DOI:10.16535/j.cnki.dlhyxb.2016.03.019
文章编号:2095-1388(2016)03-0338-06
收稿日期:2016-03-25
基金项目:国家自然科学基金资助项目 (51422901)
作者简介:胡伟 (1968—),男,工程师。E-mail:190045408@qq.com
Numerical study of nonlinear wave force on ellipse caisson
HU Wei1,JI Shi-ming2,REN Xiao-zhong3,WANG Qi4,MA Yu-xiang5
(1.Construction Management Department,Dalian Ocean University,Dalian 116023,China;2.No.3 Engineering Co.Ltd.,First Harbor Engineering Co.Ltd.,China Communications Construction Co.,Dalian 116083,China;3.Dalian Jiucheng Municipal Design Co.Ltd.,Dalian 116000,China;4.School of Naval Architecture and Ocean Engineering,Faculty of Vehicle Engineering and Mechanics,Dalian University of Technology,Dalian 116024,China;5.State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian 116024,China)
Abstract:A three dimensional numerical model of interaction of nonlinear wave with structures was developed in this paper to investigate the wave force on ellipse caisson.Navier-Stokes equations were established by a finite difference method,the problem of structure surface boundary was dealt by a partial cell method and the volume of fluid(VOF)method was employed to trace the free surface.The numerical model was verified by calculation of the wave force on circular caisson,and is used to investigate the effects of the relative wave height(H/d),relative caisson width(kD),and relative length-width ratio(B/D)on the wave forces of the ellipse caisson.It was shown that the relative wave height had a significant effect on the wave forces of the caisson,with the increase in the relative wave height,with more obvious nonlinear characteristics.Compared with the non-dimensional inline wave force,the relative length-width ratio was found to have significant influence on the non-dimensional transverse wave force.Since it is very important to consider the characteristics of wind wave and sheltering conditions for selecting the appropriate relative length-width ratio,ensuring the structure having enough safety coefficient,the numerical model in this paper can be used to calculate the wave force on ellipse caisson.
Key words:ellipse caisson;wave force;VOF method;partial cell method
