基于压缩感知的微波暗室稀疏阵列RMA成像
2016-07-22谭歆冯晓毅王保平程伟方阳
谭歆, 冯晓毅, 王保平, 程伟, 方阳
(1.西北工业大学 电子信息学院, 陕西 西安 710129; 2.陕西科技大学 电气与信息工程学院, 陕西 西安 710021)
基于压缩感知的微波暗室稀疏阵列RMA成像
谭歆1,2, 冯晓毅1, 王保平1, 程伟1, 方阳1
(1.西北工业大学 电子信息学院, 陕西 西安710129; 2.陕西科技大学 电气与信息工程学院, 陕西 西安710021)
摘要:稀疏阵列天线可有效降低微波成像系统规模和处理复杂度,但成像过程中,方位孔径数据采样率无法满足Nyquist采样定律要求时,将导致成像结果模糊或者混叠。对此,提出一种基于压缩感知理论的微波暗室稀疏阵列RMA成像算法。首先在微波暗室中搭建稀疏阵列天线成像模型,其次将方位向稀疏采样回波数据进行幅度校正和相位误差补偿,然后通过压缩感知理论进行回波信号的高精度重构,最终完成RMA成像。该算法实现以较大的空间采样间隔的稀疏阵列RMA高分辨成像,并利用微波暗室实测数据验证了所提算法的可行性和有效性。
关键词:压缩感知(CS);微波暗室;稀疏阵列天线;RMA成像;信号重构
RMA(又称ω-k)成像算法是利用空间谱域数据重建目标场景图像的高精度SAR成像算法。对于点散射目标模型,RMA算法没有引入其他近似条件,可实现无几何变形的完全聚焦,因此是SAR成像的最优实现。其在宽孔径、大斜视角[1-2]条件数据处理的优势,非常适合进行阵列天线成像。
稀疏阵列成像能够以较少天线阵元数目获得较长的虚拟阵列合成孔径来进行成像,达到与满阵天线接近的成像效果,从而减轻信号处理的负担,在尽可能减少主瓣展宽的同时,更好的抑制旁瓣,确保系统性能,达到有效降低系统成本的目的[3]。但是,天线阵列的稀疏化必然造成空间采样的缺失,当方位孔径采样数据无法满足Nyquist采样定律的要求时,会导致栅瓣出现,旁瓣电平的增高,使得成像结果出现模糊或者混叠[4],严重影响成像质量。针对稀疏阵列成像存在的问题,压缩感知(Compressed Sensing,CS)[5-6]理论被引入,CS从理论上突破了传统的Nyquist采样定理的限制,通过信号的稀疏表示、非相干测量及非线性优化重构方法,完成稀疏阵列天线回波信号的高精度重构。由于方位稀疏阵列回波信号具有稀疏性特征,并且包含目标成像所必需信息,因此能够利用CS理论进行成像处理。
在研究稀疏阵列RMA成像的过程中发现:(1)RMA成像算法所要求数据必须为空域均匀采样数据;(2)根据相位中心近似PCA(Phase Center Approximation)原理可得到等效虚拟阵元位置,但等效误差补偿不能被忽略,因此需要进行相位误差校正[7-8]。对此,本文首先在微波暗室中搭建线性稀疏阵列天线成像模型,再对回波数据进行相位误差校正,为了提高方位向成像质量和分辨率,通过CS理论对回波信号进行高精度重构,最终完成RMA成像。实现了以较大空间采样间隔的稀疏阵列RMA算法精确成像,并通过微波暗室实测数据对本文所提方法和结果进行了验证和分析。
1微波暗室稀疏阵列成像系统
微波成像测试系统暗室采用矩形造型结构,具体尺寸为:长度为25 m,纵深宽为15 m,高度为15 m。图1为微波暗室成像系统的结构图。天线测试系统采用收发分置的工作方式,发射阵列和接收阵列平行置于扫描架两侧,矢量网络分析仪的发射端产生的步进频率信号经过功率放大器进行放大后,直接由发射天线发射出去,含有待测目标信息的回波信号则由接收天线送入矢量网络分析仪接收端。测试实验中采用的天线子阵元尺寸为10 cm×7 cm。

图1 微波暗室成像系统结构图
为了对稀疏阵列天线通过孔径综合方法进行成像,兼顾实验系统的复杂度,采用2组每组5个天线子阵元分别作为发射和接收阵列,稀疏布置在1、2、4、6、7的位置节点,具体分布位置如图2所示。方位向子阵元最小间隔尺寸为10 cm,若采用多发多收工作模式可以获得等间距为5 cm线性均匀分布的13个等效虚拟相位中心。图3是待测目标为3个三面角反射器。
2稀疏阵列天线信号模型
稀疏阵列天线几何模型如图4所示,发射、接收阵列分布于X轴两侧,与X轴间距为Δy,子阵元间最小间隔为d,待测目标中心距离原点O的距离R0,则收发阵元与目标中心的距离为
(1)
2.1相位误差补偿校正
微波暗室中发射天线和接收天线阵元的位置偏差,将引起相位误差。导致方位向聚焦不准确,成像质量下降,严重时将导致方位向无法聚焦。
由于阵列天线收发分置,接收阵元得到来自发射阵元的目标回波信号。其多普勒相位历程表达关系为(2)式所示。
(2)
收发分置的天线阵元根据PCA原理可以等效为13组在X轴上间隔为5 cm均布的收发共置的等效虚拟天线阵元,由于收发双程,则其相位历程为(3)式所示
(3)
由于本次微波暗室测试实验不符合远场测试条件,等效误差不可忽略,因此需要进行相位误差校正。等效相位中心误差Δφ表达关系如(4)式所示。
(4)
相位误差校正过程就是将等效相位中心误差Δφ进行补偿。
利用阵列天线接收的回波信号进行成像,不仅要求进行相位误差校正,而且要求各通道增益相同,但是微波暗室实测中各通道数据幅度存在一定的差异,为了确保阵列天线的成像性能,因此需要在成像处理前对各方位向通道获取的数据进行幅度误差的校正,即通过对各通道接收信号的输出功率进行归一化处理,以消除各通道不一致性所带来的影响。
2.2回波信号模型
通过幅度校正和相位误差补偿处理之后,可得到13组沿X轴均匀分布的等效虚拟天线阵元接收的回波信号,如图5所示。在高频区,待测目标可视作多个强散射点的线性叠加[9],在不考虑散射点之间的相互影响下,假设目标区域某点的反射系数表示为σ(x,y),则接收天线在(xa,kr)位置接收的回波信号为s(xa,kr)。
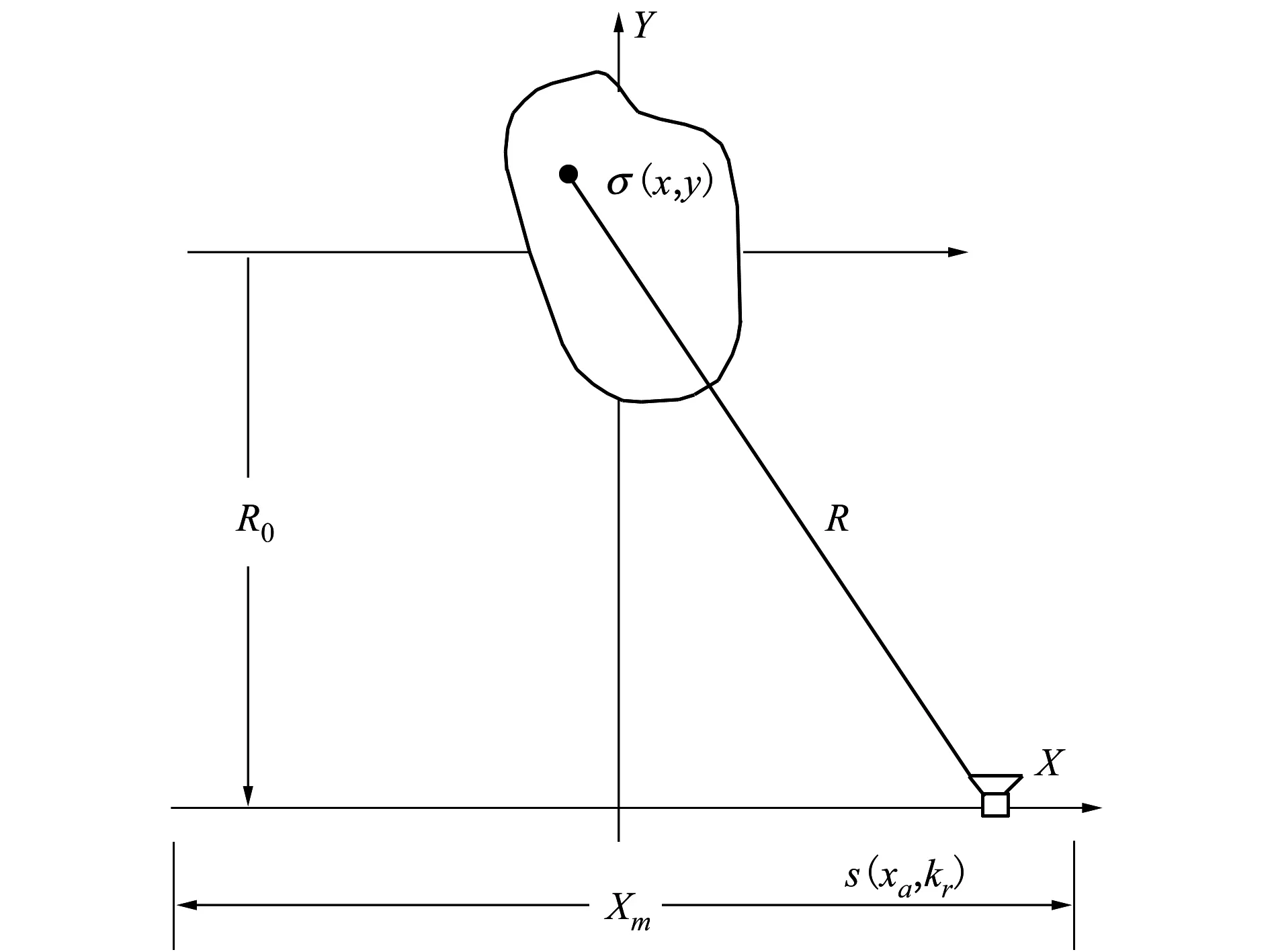
图5 回波信号模型图
回波信号具体表达关系如(5)式所示
(5)

正因为RMA是在空间谱域进行的高精度SAR成像算法,因此需要将斜距频域-方位时域回波数据s(xa,kr)沿方位向xa进行傅里叶变换,将得到方位频域回波数据S(kx,kr),以此作为RMA成像算法所要求的谱域回波数据,具体表达关系如(6)式所示。
(6)
3压缩感知RMA成像

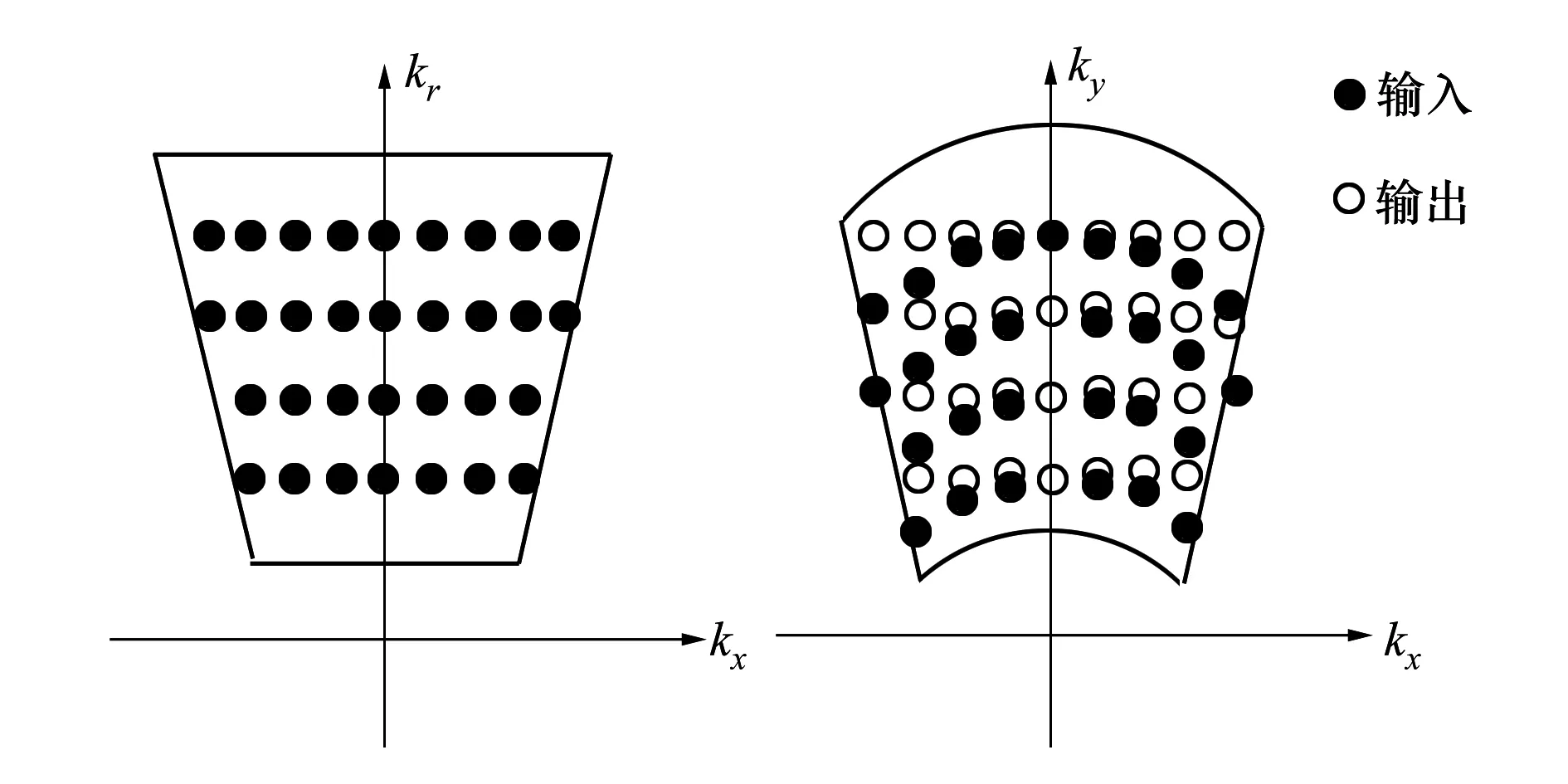
图6 Stolt插值过程
根据RMA算法的基本原理,具体实现过程主要有以下步骤:
1) 通过二维FFT将信号变换到二维频域;
2) 参考函数相乘,即匹配滤波;
3) 在频域进行Stolt插值;
4) 二维IFFT将信号转换到空间域。
由于孔径综合后,方位向稀疏阵列采样回波数据如果不满足Nyquist采样定理要求,将会造成成像结果的混叠和模糊,直接影响了目标方位向分辨率。为了提高目标成像的聚焦能力,提升成像质量水平,本文采用压缩感知方法进行处理,即利用CS理论对稀疏阵列回波信号进行高精度恢复重构。
相对于整个目标成像场景而言,强散射目标仅占有很小一部分,目标点在多普勒频域仅有少数频点为有效信号,而其他频点则为冗余信息。因此等效虚拟阵列回波信号s(xa,kr)可以被认为CS理论所要求稀疏信号。傅立叶基空间是压缩感知雷达成像时最直观、最有效的稀疏基空间,(7)式为基空间具体表达式。
(7)
式中,fm表示信号频率,tn代表方位向采样时间。N维阵列回波信号s在稀疏基空间Ψ下的稀疏表示为(8)式所示。
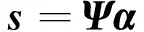
(8)
α表示阵列回波信号s在稀疏基空间Ψ下的稀疏系数向量,在α中,仅有K(K≪N)个非零值。因此当N维回波信号s经过测量矩阵进行降维观测后,可以得到M维观测信号,其中M (9) 图7 基于压缩感知的微波暗室RMA成像算法流程 4微波暗室实验结果和分析 通过微波暗室实测数据来验证本文所提方法的可行性和有效性。设定微波暗室成像系统工作频段为Ku波段,发射带宽为6GHz的步进频率信号。通过控制系统开关,以分时方式控制天线阵元完成单发多收,用以模拟天线阵列多发多收的过程。收发分置的稀疏天线阵列根据孔径综合后得到13组等间隔为5cm收发同置的等效虚拟线性天线阵列,即方位向综合孔径长度为0.6m。 由于方位向的13组通道采样数据无法满足Nyquist采样定律的要求,导致成像结果模糊或者混叠,因此通过给方位向数据规模进行扩维,在原有13组通道数据基础上采用等间隔插入12组0数据,将方位向采样数目变为25组,即等效虚拟天线阵列线性空间间隔为2.5cm。除了方位向采样数据维数扩大之外,微波暗室测试系统其余参数均未改变,仍然满足RMA成像中空域数据均匀采样的要求。 微波暗室成像系统各参数设置,如表1所示。 表1 微波暗室成像系统参数 本次测试所使用数据为[1,3,4,6,7,8,10,12,13]共9组通道的回波数据作为方位向随机采样数据,然后将其扩展为25组回波数据,这其中16组数据为0,以此作为稀疏随机采样数据,应用稀疏阵列RMA成像算法进行目标成像,其成像结果为图8所示,而利用本文所提方法成像的结果则如图9所示。 图8 稀疏阵列数据RMA成像结果 为了定量的分析评价本文所提成像方法对目标成像质量的影响,通过采用基于点目标模型的评价指标,即峰值旁瓣比(PSLR)和积分旁瓣比(ISLR)来进行分析对比,其结果如表2所示。 图9 本文所提方法成像结果 成像方法PSLR/dBISLR/dB稀疏阵列RMA成像-8.7459-7.3668本文所提方法成像-15.1872-13.5254 综合以上结果可知,对于相同数据量的方位向稀疏阵列回波数据,利用传统RMA成像方法得到的结果,不仅方位向旁瓣较高,而且目标分辨率较差,成像质量模糊。而利用本文所提的基于压缩感知理论的成像方法则有效抑制了旁瓣,提高了目标像的聚焦准确性,实现了稀疏阵列天线的高分辨成像,取得了更好的成像质量。 5结论 本文在微波暗室搭建了稀疏阵列天线成像系统模型,利用微波暗室实测数据,对基于压缩感知理论的稀疏阵列天线成像算法的可行性和有效性进行了验证与分析。针对天线阵列成像中存在幅度误差进行了统一校正,相位误差给出了具体的误差补偿方法并完成相位误差补偿。针对方位向回波信号欠采样或者稀疏采样,利用压缩感知信号重构理论对稀疏阵列天线回波信号的高精度重构,最终完成目标的RMA算法成像,通过方位向准确聚焦,得到成像效果更佳目标像。实现了较大的空间采样间隔稀疏阵列RMA高分辨成像。 此外,本文的研究工作对于在微波暗室的稀疏阵列成像的实际应用具有一定的参考意义和价值。 参考文献: [1]保铮, 邢孟道, 王彤. 雷达成像技术[M]. 北京:电子工业出版社, 2005 BaoZheng,XingMengdao,WangTong.RadarImagingTechnology[M].Beijing,PublishingHouseofElectronicsIndustry, 2005 (inChinese) [2]CumimingIanG,WongFrankH. 合成孔径雷达成像-算法与实现[M]. 洪文,译. 北京: 电子工业出版社, 2007 CumimingIanG,WongFrankH.DigitalProcessingofSyntheticApertureRadarDataAlgorithmsandImplementation[M].HongWen,Translator.Beijing,PublishingHouseofElectronicsIndustry, 2007 (inChinese) [3]侯颖妮, 李道京, 洪文,等. 稀疏阵列微波暗室成像实验研究[J]. 电子与信息学报, 2010, 32(9):2258-2262 HouYingni,LiDaojing,HongWen,etal.ThinnedArrayImagingExperimentalStudyinAnechoicChamber[J].JournalofElectronics&InformationTechnology, 2010, 32(9):2258-2262 (inChinese) [4]胡大海, 杜刘革, 常庆功, 等.MIMO成像技术的插值方法研究[J]. 微波学报, 2014, 30(6):36-40 HuDahai,DuLiuge,ChangQinggong,etal.StudyontheInterpolationMethodofMIMOImaging[J].JournalofMicrowaves, 2014, 30(6):36-40 (inChinese) [5]DonohoDL.CompressedSensing[J].IEEETransonInformationTheory, 2006, 52(4): 1289-1306 [6]CandesEJ,RombergJ,TaoT.RobustUncertaintyPrinciples:ExactSignalReconstructionfromHighlyIncompleteFrequencyInformation[J].IEEETransonInformationTheory, 2006, 52(2):489-509 [7]王怀军, 朱宇涛, 许洪波, 等.MIMO雷达等效相位中心误差分析[J]. 电子与信息学报, 2010, 32(8):1849-1854 WangHuaijun,ZhuYutao,XuHongbo,etal.AnalysisofDisplacedPhaseCenterErrorinMIMORadar[J].JournalofElectronics&InformationTechnology, 2010, 32(8):1849-1854 (inChinese) [8]董会旭, 张永顺, 冯存前, 等. 基于线阵MIMO-ISAR二维成像方法[J]. 电子与信息学报, 2015, 37(2): 309-314 DongHuixun,ZhangYongshun,FengCunqian,etal.Two-DimensionalImagingUsingMIMORadarandISARTechniqueBasedonLinearArray[J].JournalofElectronics&InformationTechnology, 2015, 37(2): 309-314 (inChinese) [9]TarchiD,OliveriF,SammartinoPF.MIMORadarandGround-BasedSARImagingSystems:EquivalentApproachesforRemoteSensing[J].IEEETransonGeoscienceandRemoteSensing, 2013, 51(1): 425-435 收稿日期:2015-09-24基金项目:国家自然科学基金(61472324、61401360)及中央高校基本科研业务费专项资金(3102014JCQ01055)资助 作者简介:谭歆(1978—),西北工业大学博士研究生,主要从事微波雷达成像及压缩感知雷达信号处理的研究。 中图分类号:TN957 文献标志码:A 文章编号:1000-2758(2016)03-0374-06 Thinned Array Antennas RMA Imaging in Microwave Anechoic Chamber Based on Compressed Sensing Tan Xin1,2, Feng Xiaoyi1, Wang Baoping1, Cheng Wei1, Fang Yang1 1. School of Electronics Information,Northwestern Polytechnical University,Xi'an 710129,China2. School of Electronical and Information Engineering,Shaanxi University of Science and Technology,Xi'an 710021,China Abstract:The thinned array antennas can effectively reduce the scale and processing complexity of microwave imaging system, but it will lead to image blur or aliasing while the data sampling rate of azimuthal aperture can not meet the requirements of the Nyquist sampling theorem in the imaging process. Thus, thinned array antenna RMA imaging algorithm for the microwave anechoic chamber based on Compressed Sensing is proposed in the paper. Firstly, thinned array antenna imaging system model in the microwave anechoic chamber is established, secondly, amplitude correction and phase error compensation about the sparse sampling azimuthal echo data is accomplished, then echo signal is reconstructed precisely by Compressed Sensing theory, the final RMA imaging is obtained. The larger space sampling interval thinned array RMA high resolution imaging is achieved by the algorithm, and the data from microwave anechoic chamber is used to verify the validity and feasibility of the algorithm. Keywords:Compressed Sensing(CS); microwave anechoic chamber; thinned array antennas; RMA imaging algorithm;signal reconstruction