基于时间序列分析的桥梁长期挠度分离与预测

陈国良， 林训根， 岳　青， 刘　华

(1. 中国矿业大学 环境与测绘学院， 江苏 徐州 221116； 2. 中铁大桥勘测设计院集团有限公司， 湖北 武汉 430050)



基于时间序列分析的桥梁长期挠度分离与预测

陈国良1， 林训根1， 岳青2， 刘华2

(1. 中国矿业大学 环境与测绘学院， 江苏 徐州 221116； 2. 中铁大桥勘测设计院集团有限公司， 湖北 武汉 430050)

摘要：针对挠度长期监测信号的多尺度特性及温度荷载下挠度周期性变化的特点，利用修正平均周期图法获取信号分量周期长度，结合基于中心移动平均法的挠度温度效应分离策略，提取结构变形特征，运用ARIMA模型建立结构变形趋势的预测模型.以黄冈长江大桥为例，讨论了温度与挠度的相关性，通过模拟数值试验验证分离算法的有效性.实测数据的处理与分析结果表明，本文方法具有较高的可靠性和精度，可为桥梁进行损伤识别提供数据支持.

关键词：挠度； 分离； 长期趋势； ARIMA模型； 预测

挠度是桥梁结构健康监测中最能直观反应结构安全状态的参数，直接反映了结构的整体竖向刚度、承载能力.运营期监测的桥梁挠度信号是环境荷载、车辆荷载、材料劣化、噪声等因素共同作用下的综合响应[1-2].准确分离桥梁在各个因素作用下的挠度特性、预测结构长期变形趋势，有助于桥梁工作性能评估和结构安全预警.结构运行状态与环境参数密切相关，因而针对挠度信号的分离与预测是近年来研究的热点之一.文献[3-5]在分析长期监测数据的基础上得出挠度与温度并非一般的线性关系，采用主成分分析法讨论温度的作用规律，却未从监测数据中提取温度影响成分，缺乏定量评价；Tang[6]应用经验模态分解对信号进行通道扩展构建基于独立分量分析的挠度分离模型，但在实际应用中区别特征信号与虚假信号的固有模态分量存在一定难度；梁宗保[7]通过建立相位差为半个日周期的挠度-温度效应回归方程，从而剔除结构信息中的温度效应，但对于长期监测而言，相位差并非均匀的半个日周期，因而无法确保回归方程的准确性；刘夏平等[8]研究了基于奇异值分解的盲信号分离方法，然而其忽略了构建分解矩阵时对分离信号周期长度的讨论；文献[9-11]分别提出了自适应带宽滤波法、最小二乘支持向量机、多最小二乘支持向量机进行挠度-温度效应分离的方法，但算法较为复杂，实用性不足.

本文利用挠度各响应分量在时间尺度上不耦合的特点，提出了基于时间序列分析的挠度分离与预测方法，实现挠度-温度效应的有效分离，从而定量评价结构变形特征，再以求和自回归滑动平均(autoregressive integrated and moving average,ARIMA)模型进行精确拟合，准确预测桥梁变形趋势，为桥梁挠度-温度效应的分离及长期趋势的预测提供了一种思路.

1挠度响应分析

1.1挠度响应加法模型

随着桥梁服役期限的增加，预应力逐渐损伤、混凝土收缩徐变、温度变化等原因，主跨跨中均存在不同程度的下挠，影响行车安全，因而长期挠度变形是桥梁结构监测的重要一环.健康监测系统获得的挠度数据包含了温度荷载、车辆荷载、结构劣化效应等信息.温度效应是结构在外界环境影响下产生温度变化而引起结构不受构件约束的均匀变形，一般认为自然环境下的温度荷载(Tt，t为时间.)包括日温差荷载(Td)、年温差荷载(Ty)及骤然升降温荷载(Tu).车辆荷载(Vt)属于随机影响因素，大跨度桥梁结构趋于柔性，对于铁路桥梁而言，列车荷载造成的瞬时下挠较为突出，文献[7]提出利用小波理论，根据挠度信号中温度效应与活载效应时频特征的不同，将监测信号进行多尺度分解，提取实际测量信息中的活载效应.挠度的变化趋势(Lt)具有长期不稳定的特点，通常只能对变形的影响程度做出定性分析，而准确预测结构长期变形存在一定难度.

结构响应的各个影响因素具有多尺度的特征，例如温度效应的周期包含日周期和年周期等，而结构的长期变形有可能长达数月甚至数年，通常视各类效应在时间尺度上并不耦合，即某一荷载所产生的变形不受同时作用的其他荷载的影响，因此选择加法模型[8]作为挠度响应时间序列Xt的表达.

(1)

式中：Nt为环境噪声.

1.2分离策略

挠度分离策略采用逐一剥离的方法.首先，利用小波分析剔除活载效应与环境噪声，再利用时间序列分析的中心移动平均法分离日温差效应和年温差效应，最后获得挠度变形的长期趋势项.

设挠度响应时间序列观测值为{Xt,t=1,2,…,n}，其中n为观测值总数.在准确确定周期长度(T)的情况下，移动平均法可以在很大程度上削弱或消除原有序列中的温度效应周期项[12]，使时间序列趋于平滑，从而得到监测信号中的长期趋势特征.环境噪声与车辆荷载都属于高频信号，采用修正平均周期图法(Welch法)对经过小波滤波后的挠度信号进行频谱分析可以准确获得信号的频域分布信息，转化为周期长度，作为中心移动平均的移动步长参数.以序列起点进行移动平均会导致分离结果存在滞后性，因此本文提出对移动平均的时间相位进行半周期延迟，即以周期中点为起点进行移动平均，以规避这种缺陷，时域相位延迟长度需根据相应分离效应的周期进行调整.时序中含有多种周期成分，应针对各个周期进行数次移动平均，由式(2)计算得到各个频率所对应中心移动平均产生的各挠度效应分量值，依次从原始序列减去求得的各个中心移动平均序列，最后得到趋势项.移动平均流程如图1所示.

图1　移动平均流程图

其中，第t期的移动平均值为

(2)

2挠度变形趋势预测模型

时间序列分析从动态角度描述某一现象的内在数量关系及变化规律，由于建模过程简单、预报精度高，因而广泛应用于变形监测的数据处理中.桥梁挠度变形是以时间为特征的数据集，影响因素多样，形变机理复杂，难以用确定性的函数进行表达，但长期监测数据在统计上具有一定的相关关系，因此可采用时间序列分析方法来表征桥梁结构的特性.设{Xt,t=1,2,…,n}是零均值的平稳序列，其值与前p阶的值和前q阶的干扰项有关，根据多元线性回归的思想，可得ARMA(autoregressive and moving average)模型[13].

(3)

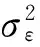
ARMA模型要求建模的基础数据具有平稳性，即序列的统计特征不随时间的推移而发生改变.而一般的工程数据，如桥梁挠度变形，由于受到自身结构特点及外界环境因素影响，无法满足条件，需要进行平稳化处理，本文采用差分法，设Xt经过d次差分后得到平稳的新序列Yt，则

(4)

式中：B为后移算子，BdXt=Xt-d，d为差分阶次.将Yt代入式(3)中进行建模，即得到ARIMA模型.ARIMA模型的建立主要包括以下4个步骤.

(1) 平稳性检验.平稳性检验可通过时序图直接判读，也可利用单位根检验来判断，常用的单位根检验方法有DF(Dickey-Fuller)检验法和ADF(augmented Dickey-Fuller)检验法.

(5)

(6)

(7)

(8)

式中：ε*为残差向量；β为待估参数;Q为残差平方和；βk为第k次参数计算结果.

A中的各元素可由下式计算得到:

(9)

实际计算时，需要设置一个合适的迭代阈值δ，βk+1-βk<δ，例如可取δ=10-4.

(3) 模型定阶AIC.AIC(Akaike information criterion)准则由日本统计学家Akaike于1974年提出，该准则体现了模型拟合的优劣程度.

(10)

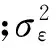
(4) 模型χ2检验.对已确定的模型进行白噪声(模型残差)检验[15].构造χ2检验的统计量

(11)

3工程应用

3.1数据来源

黄冈长江大桥为主跨567 m的钢桁梁斜拉桥，上层为公路桥面，下层为双线铁路，2014年6月建成通车后结构健康监测系统也正式开始运行，监测包含环境参数、结构动力特性、主梁挠度、拉索索力等各项内容.主梁挠度监测采用基于差压变送器的方法，仪器参考精度为0.065%(与所设置量程相关)，传感器安装如图2所示.测点布置(图3)于边跨、辅助跨跨中，主跨挠度较大，受荷载作用各点挠度变换差异明显，因此在1/4跨、跨中、3/4跨布设测点，3号塔处为基准点.

图2　传感器安装

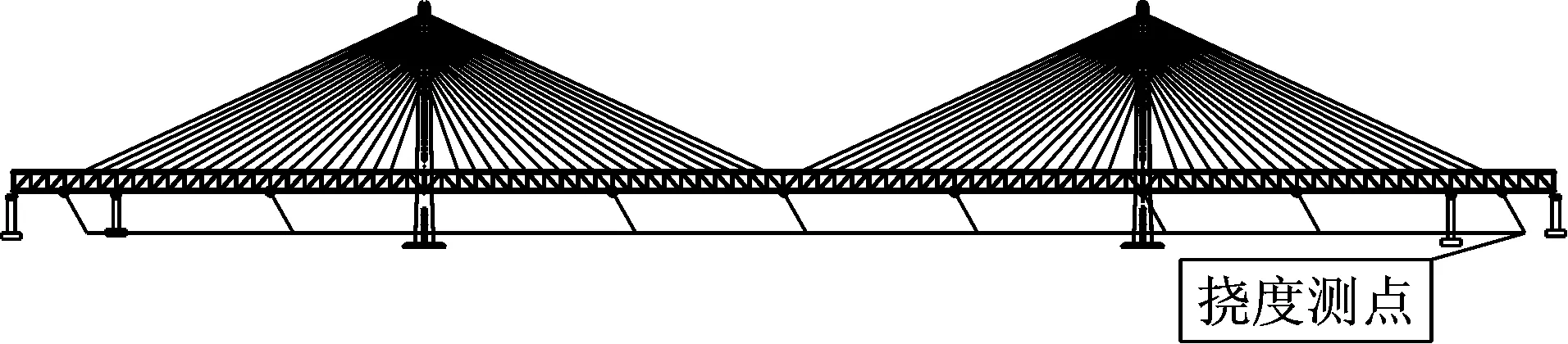
图3　测点布置

3.2挠度信号的模拟与分离

钢桁梁为超静定结构，虽然热传导性能较好，但是考虑日照辐射、结构方位、周围地理环境等因素，结构内部各构件间存在局部温差，构件间的变形相互约束，产生温度次应力，加之温度分布不均在结构各层之间产生的温度自应力，二者对结构受力的影响十分显著[16].钢桁梁斜拉桥构造复杂，准确计算温度效应存在较大的困难，利用实测数据通过相关性分析可以得到温度荷载下钢桁梁的挠度行为.图4为黄冈长江大桥典型挠度日变化趋势图，可以看出实测数据与上文挠度加法模型的描述较为符合，日变化趋势表现为规则的正弦曲线，而列车荷载在跨中产生的瞬时下挠可达40 mm.

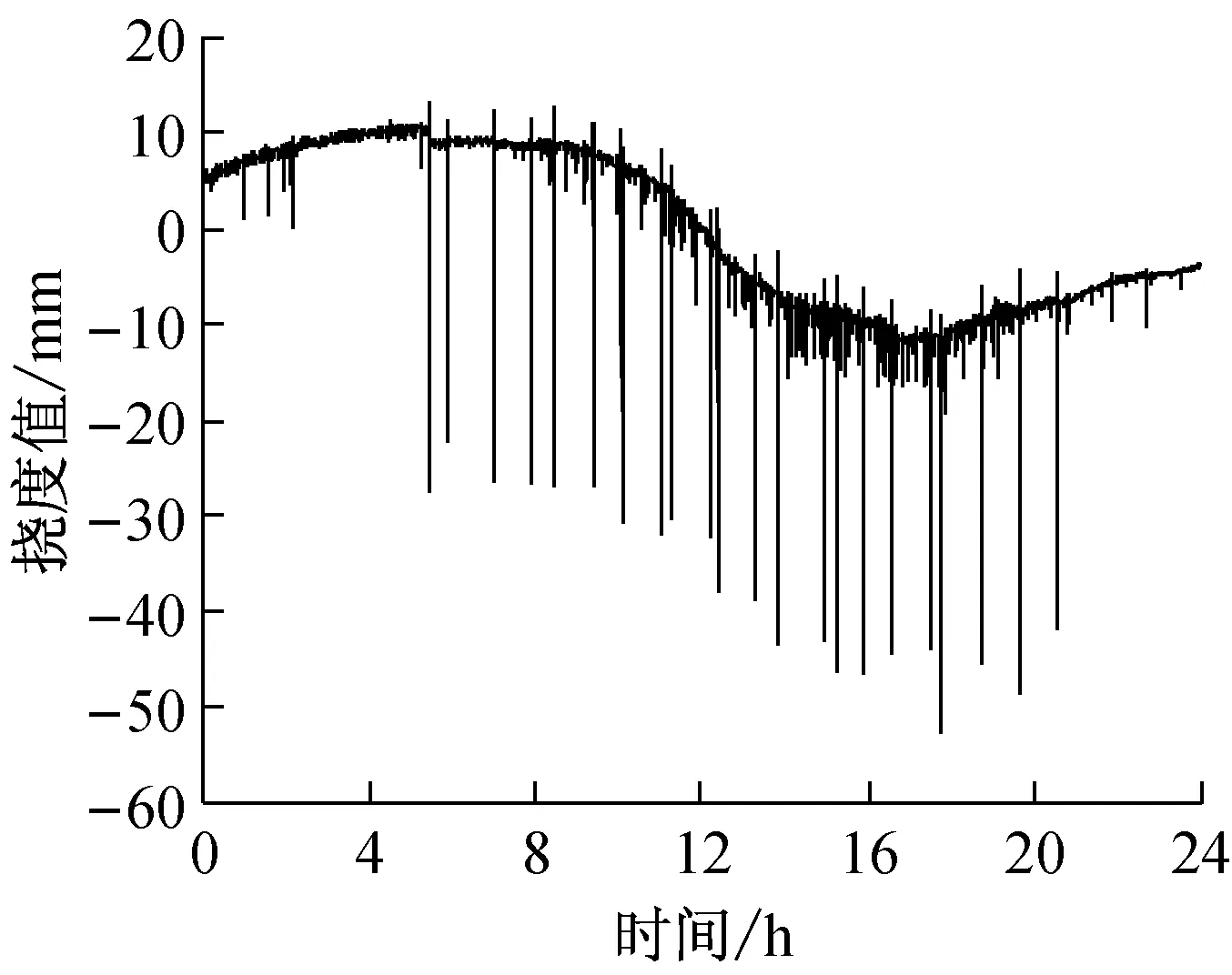
图4　典型挠度日变化时程

对于温度与挠度的相关性(如图5所示)，虽然二者存在一定的线性关系，但其区间很宽，回归估计的精确性较低，因而通过建立温度与挠度回归模型以剔除温度荷载的做法并不适用.但回归分析的结果可以用来估计单位温度影响下挠度的大致改变量，作为数值模拟的依据，结合温度变化规律，进而得到模拟挠度值.拟合线性模型为

f=-2.68w+79.73

(12)

式中：f为挠度;w为温度.由模型可知，当升温1℃时，主跨跨中将产生2.68 mm(设为d)的下挠.

图5　温度与挠度相关性散点图

考察黄冈地区气候条件，结合年度温度变化的规律，设1 d中整体日照温度变化wd在0～16℃，年温差wy为30～40℃，温度均为正弦变化的周期函数(以1 s为1 h计)，温度与桥梁结构变形之间关系按回归分析结果来考虑.根据挠度加法模型，总挠度f0由日温差效应(f1)、年温差效应(f2)及长期下挠(f3)构成，假设随着时间的推移，长期挠度将趋于平稳，因此利用幂函数来拟合长期变形趋势.综上所述，可得模拟挠度各分量的计算公式为

(13)

式中：t为时间，采样频率为1 Hz，模拟的总挠度信号f0如图6所示.

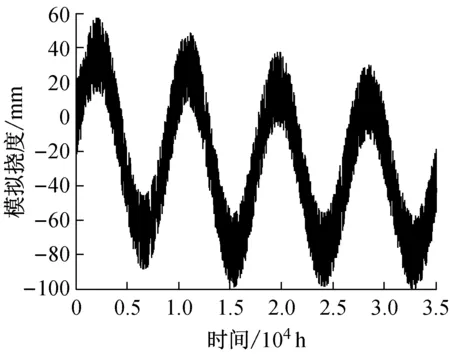
图6　总挠度模拟值

采用Welch法对f0进行频谱分析，要准确确定周期长度，要求频率分辨率尽量要高，应增加进行快速傅里叶变换(FFT)的点数，窗函数选择Hanning窗，窗口长度与FFT计算点数相等，分段序列重叠长度取窗口长度一半，结果如图7.按照1.2节中的策略对f0进行分离，各挠度分量与模拟值比较如图8～10，可见分离值与模拟值的曲线波动规律基本一致.但考虑到不同随机幅值的波动影响到分离结果的优劣，为检验算法的可靠性，进行100次试验，统计试验中模拟值与分离值的相关系数，结果如表1.日温差效应、年温差效应及趋势项模拟值与分离值的相关系数在0.8以上的占了100%，表明分离值与模拟值存在强相关，算法的分离结果验证了中心移动平均算法用于挠度分离的可靠性与有效性.

3.3实测数据的分离

以主跨跨中测点为例，由于系统连续、实时运行，采集的数据量较大，先利用小波分析理论剔除列车荷载和噪声的影响，再以1 h平均值作为该时段的特征值.图11为2014年7月7日至9月10日的监测数据，其总体呈现连续正弦曲线的波动特征，短期内受温差影响幅值有所变化，但周期长度较为稳定，这为温度效应的分离提供了基础.实测数据的时间跨度为数月，从频域信息中获得日温差效应挠度的周期仍然近似于1“天”，而长期温度效应的周期长度则接近于“月”，因此以“月”周期代替“年”周期进行长期温度效应的分离，分离后的各挠度分量如图12a至12c所示.

图7　模拟信号的频谱分析

图8　日温差效应分离前后对比

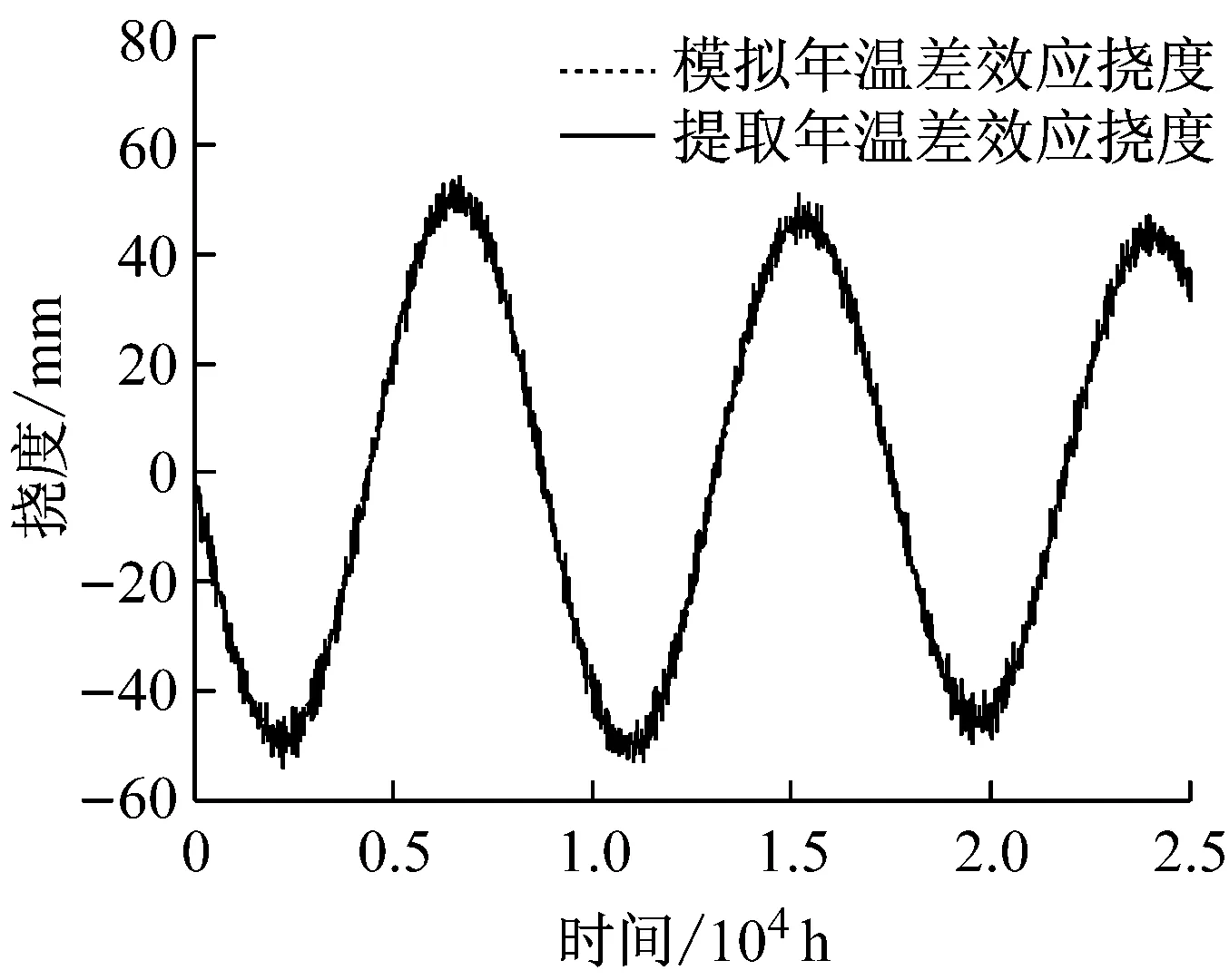
图9　年温差效应分离前后对比

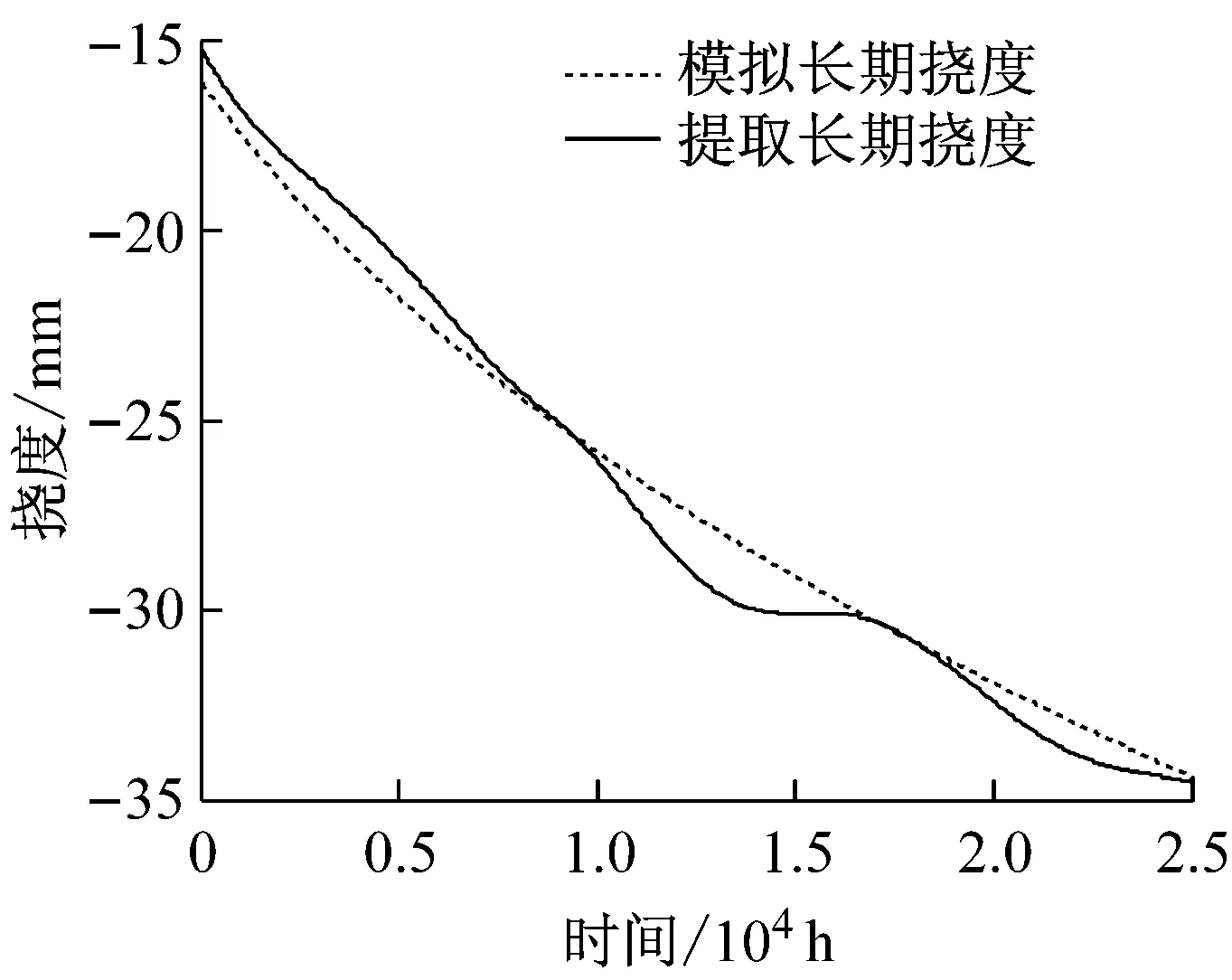
图10　长期趋势分离前后对比

表1　试验相关系数统计

图11　挠度长期观测数据

由图12可见，分离的日温差效应较平稳，相邻时刻的幅值也十分接近，月温差效应的频率明显大于日温差效应，与实际相符，分离出的趋势项总体表现为上拱，这由于以“月”代替“年”作为长期温度效应周期而导致短期温差无法消除，主梁表现为受降温影响而产生上拱.采用中心移动平均法对实测温度数据进行分离，这里不考虑骤然温差的影响，分离出日温差变化和月温差变化，结果如图12d至12f，剔除日温度变化、年温度变化后的残余温度整体为降温趋势，符合温度的季节特性，同时与回归分析及挠度的分离结果相吻合，这印证了主梁长期趋势变化的根源，从另一面也验证了分离算法的正确性.

3.4长期趋势的预测

将提取的挠度长期趋势进行模型拟合，经过试验计算，选取500个数据作为建模基础数据拟合效果较好.由图12c可知原始数据具有明显的趋势项，经过二阶差分后，时序的ADF统计检验量为-4.073，小于1%时显著水平的临界值，表明二阶差分后时序为平稳序列，满足建模条件.设定模型初始阶数，由低阶至高阶拟合，由于低阶模型就能以较高精度实现拟合，因此限定拟合最高阶次.分别计算各模型AIC值，部分模型AIC值如表2.搜索模型中AIC最小值，当p=4，q=5时，AIC取到最小，则模型应为ARIMA(4，2，5)，进行卡方检验，残差服从正态分布，模型检验通过.从图13可知，模型的拟合效果良好.对后50期的数据进行预测，由图14可知其短期预测残差未超过1 mm，最大相对误差为8.61%，而前20期中相对误差均小于5%，但随预测期数的增加预测残差也随之增大，实际操作中可采用加窗的方法，以20期为间隔，更新模型的起算数据，可有效提高预测精度.

a 日温差效应挠度

b 月温差效应挠度

c 挠度长期趋势

d 日温差变化

e 月温差变化

f 残余温度

表2　部分模型AIC值统计

4结论

针对现有挠度温度效应分离算法研究不足、实用性差的问题，提出基于中心移动平均法的挠度-温度效应分离策略，将Welch法获得的信号分量周期长度作为移动平均半周期延迟的参数，避免了移动平均的滞后性，实现移动步长的自动确定.通过多次数值模拟试验，得到模拟值与分离值存在强相关的结论，验证了算法的有效性.同时根据桥梁结构长期变形趋势不稳定的特点，以实测数据为研究对象，采用时间序列分析建立了挠度趋势的ARIMA预测模型，模型拟合效果较好，预测精度高，可为桥梁的结构安全提供预警.

图13　模型拟合效果

图14　模型预测残差值

参考文献:

[1]陈宏玉,黄腾,李桂华. 基于灰关联GM(1,N)模型的特大跨径桥梁挠度变化分析[J]. 测绘通报,2009,55(1):31.

CHEN Hongyu,HUANG Teng,LI Guihua. Analysis of oversize span bridge deflection based on grey relation GM(1,N)[J]. Bulletin of Surveying and Mapping,2009,55(1):31.

[2]宗周红,钟儒勉,郑沛娟,等. 基于健康监测的桥梁结构损伤预后和安全预后研究进展及挑战[J]. 中国公路学报,2014,27(12):46.

ZONG Zhouhong,ZHONG Rumian,ZHENG Peijuan,etal. Damage and safety prognosis of bridge structures based on structural health monitoring[J]. China Journal of Highway and Transport,2014,27(12):46.

[3]James M W, Brownjohn,Ki-Young Koo,etal. Operational deformations in long-span bridges[J]. Structure and Infrastructure Engineering, 2015, 11(4): 556.

[4]Ghali A,Elbadry M,Megally S. Two-year deflections of the Confederation Bridge[J]. Canadian Journal of Civil Engineering, 2000, 27(6): 1139.

[5]E J Cross,K Y Koo,J M W Brownjohn,etal. Long-term monitoring and data analysis of the Tamar Bridge[J]. Mechanical Systems and Signal Processing, 2013, 35(1): 16.

[6]Tang C H, Yang H, Liu X P,etal. Separation of bridge deflection signals based on ICA[J].Advanced Materials Research, 2011, 374-377(10): 2090.

[7]梁宗保．基于监测信息统计分析的桥梁结构安全评价研究[D]．重庆:重庆大学,2006.

LIANG Zongbao. Research based on the monitoring information statistics and analysis of the bridge structure safety evaluation[D]. Chongqing: Chongqing University,2006.

[8]刘夏平,杨红,孙卓,等. 基于奇异值分解的桥梁挠度分离研究[J]. 中山大学学报:自然科学版,2013,52(3):11.

LIU Xiaping,YANG Hong,SUN Zhuo,etal. Separation study of bridge deflection based on singular value decomposition[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni,2013,52(3):11.

[9]刘纲,邵毅敏,黄宗明,等. 长期监测中结构温度效应分离的一种新方法[J].工程力学,2010,27(3):55.

LIU Gang,SHAO Yimin,HUANG Zongming,etal. A new method to separate temperature effect from long-term structural health monitoring data[J]. Engineering Mechanics,2010,27(3):55.

[10]刘夏平,杨红,孙卓,等. 基于LS-SVM的桥梁挠度监测中温度效应分离[J]. 铁道学报,2012,34(10):91.

LIU Xiaping,YANG Hong,SUN Zhuo,etal. Study on separation of bridge deflection temperature effect based on LS-SVM[J]. Journal of the China Railway Society,2012,34(10):91.

[11]杨红,孙卓,刘夏平,等. 基于多最小二乘支持向量机的桥梁温度挠度效应的分离[J]. 振动与冲击,2014,33(1):71.

YANG Hong,SUN zhuo,LIU Xiaping,etal. Separation of bridge temperature deflection effect based on M-S-SVM[J]. Journal of Vibration and Shock,2014,33(1):71.

[12]彭令,牛瑞卿,吴婷. 时间序列分析与支持向量机的滑坡位移预测[J]. 浙江大学学报:工学版,2013,47(9):1672.

PENG Ling,NIU Ruiqing,WU Ting. Time series analysis and support vector machine for landslide displacement prediction[J]. Journal of Zhejiang University:Engineering Science,2013,47(9):1672.

[13]王燕. 应用时间序列分析[M]. 北京:中国人民大学出版社,2008.

WANG Yan. Applied time series analysis[M]. Beijing: China Renmin University Press,2008.

[14]曾浩. 基于时间序列分析的结构损伤诊断[D]. 武汉:武汉理工大学,2006.

ZENG Hao. Structural damage detection using time series analysis[D]. Wuhan:Wuhan University of Technology,2006.

[15]刘寒冰,李国恒,谭国金,等. 基于时间序列的边坡位移实时预测方法[J]. 吉林大学学报:工学版,2012,42(S1):193.

LIU Hanbing,LI Guoheng,TAN Guojin,etal. Real-time prediction method of slop displacement based on time series analysis[J]. Journal of Jilin University:Engineering and Technology Edition,2012,42(S1):193.

[16]陈海锋. 收缩徐变及温度作用下悬索桥钢-混组合桥面系受力性能分析[D].长沙:长沙理工大学,2013.

CHEN Haifeng. Performance analysis on the steel-concrete composite bridge deck of suspension bridge under the action of shrinkage and creep as well as temperature [D]. Changsha:Changsha University of Science & Technology,2013.

收稿日期：2015-06-29

基金项目：国家自然科学基金面上项目(41371423)；国家“八六三”高技术研究发展计划(2013AA12A201)；江苏省高校优势学科建设工程(SZBF2011-6-B35)

中图分类号：TU196+.1

文献标志码：A

Study on Separation and Forecast of Long-term Deflection Based on Time Series Analysis

CHEN Guoliang1，LIN Xungen1，YUE Qing2，LIU Hua2

(1. School of Environment Science and Spatial Informatics, China University of Mining and Technology, Xuzhou 221116， China； 2. China Railway Major Bridge Reconnaissance & Design Group Co., Ltd., Wuhan 430050， China)

Abstract：In view of the multi-scale property of deflection and the periodicity under temperature load, a strategy was proposed to separate the deflection and extract the long-term trend, which combines Welch method with Center Moving Averages Method. A prediction model of the deformation was established based on ARIMA model. Taking Bridge of Huanggang Yangtze River as an example to issue the correlation between temperature and deflection, and test of numerical simulation was made to validate the effectiveness of the algorithm. Processing and analysis of the measured data indicate that the approach of this article has high precision and reliability which could provide data support for damage identification of bridge.

Key words：deflection； separation； long-term trend； ARIMA model； forecast

第一作者： 陈国良(1977—)，男，副教授，工学博士，主要研究方向为变形监测、导航位置服务.E-mail：chglcumt@163.com