最小化完成测绘时间的卫星成像任务规划算法
2016-07-21张泽浩王继河张德新邵晓巍
张泽浩 王继河 张德新 邵晓巍
上海交通大学航空航天学院,上海200240
最小化完成测绘时间的卫星成像任务规划算法
张泽浩 王继河 张德新 邵晓巍
上海交通大学航空航天学院,上海200240

针对应急条件下的成像观测任务,考虑卫星成像条带切换时间等约束建立成像任务调度模型,以最小化完成测绘任务时间为优化目标。通过改进蚁群算法进行求解,结合实际约束、加入任务执行间隔等因素来控制转移概率。为地面运管系统提供了一种新的成像策略优化目标,能够根据不同的测绘任务以及用户需求,选择优化方案对实际卫星测绘做规划。 关键词 测绘完成时间;蚁群算法;成像规划;应急
近几年,干涉SAR成像技术趋于成熟,德国TerraSAR-X和TanDEM-X编队卫星干涉成像提供了高精度的全球高程数据。编队卫星系统不受白天,黑夜及云雾影响,可以全天候、全天时对全球进行测绘,同时可以执行应急测绘任务,然而面对复杂多样的应急测绘任务,由于成像卫星资源有限,单轨成像能力有限等因素,优化测绘策略,高效利用卫星资源成为提升卫星系统整体效益的重要内容。
优化卫星测绘策略即成像卫星调度问题是指在满足卫星各项约束条件下,针对测绘区域合理规划星载开关机时间及开关机波位,以实现卫星资源高效利用。它是一类具有时间窗口约束的组合优化问题。目前解决此类问题的方法主要有启发式算法和智能优化算法。随着研究的深入,混合智能优化算法正成为目前国内外学者的主要研究方向[1]。
国外Bansana[2]等人建立整数规划模型,以最大化任务收益为优化目标,运用深度优先搜索、动态规划对SPOT-5卫星成像调度问题求解。M.Lemaitre[3]研究了Agile Earth Satellite对区域目标的测绘调度问题,建立了约束满足模型,比较了贪婪、整数规划以及遗传算法,实验证明了遗传算法虽性能较好,但对于大规模问题求解困难。Jinbong[4]提出了二进制整数模型,采用了基于拉格朗日松弛和梯度的启发式算法。
国内贺仁杰、白保存[5]等考虑了任务间的合成观测,建立了任务规划模型。以最大化完成任务收益为优化目标,提出了快速模型退火算法和动态任务合成启发式算法对问题求解。于海、郭玉华[6]等人提出了一种新的约束修正方法求解该类问题。郝会成[7]通过混合遗传算法和蚁群算法求解敏捷卫星任务调度模型。靳肖闪[8]等人提出了一种基于拉格朗日松弛与最大分支算法的多项式时间复杂度的优化算法。冉承新[9]等研究了移动目标成像侦测任务规划问题,设计了一种基于模拟退火算法及遗传算法的改进遗传算法。张帆[10]等通过将成像需求序列对应为有向图中的成像路径,基于多个优化准则使用支配关系对成像路径质量进行综合评价,提出有效准则矢量生成算法。Liu X L[11]等提出了基于任务合成的多星调度算法,在任务合成阶段采用动态规划算法求解,任务分配阶段采用自适应蚁群算法求解。
以上研究是以最大化任务收益和最小化资源消耗为优化目标,在完成测绘任务总时间方面没有较多研究,本文针对应急测绘任务,优化卫星测绘策略。首先对测绘任务进行预处理,给出问题的形式化描述,分析各项约束条件,建立约束满足模型,以最小化完成测绘任务总时间为优化目标,对蚁群算法进行改进,结合启发式规则求解问题,最后通过实验仿真验证算法有效性,为地面运管系统提供了一种新的成像策略优化目标,能够根据不同的测绘任务以及用户需求,选择不同的优化方案对实际卫星测绘做规划。
1 问题描述与调度模型建立
1.1 问题描述
SAR成像卫星通过SAR敏感器成像。SAR 敏感器以推扫方式对地面区域进行成像,观测范围由多个载荷单幅幅宽观测范围组成,这里的载荷单幅幅宽观测的范围叫做成像条带,它的长度依赖于观测时间,它的幅宽度取决于成像的内外侧角度,如图1所示。为简单起见,假设所有的成像条带幅宽相同,卫星观测范围由固定几组成像条带组成,不同成像条带会有少量重叠。
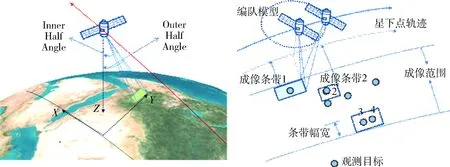
图1 卫星成像波位扫描条带及卫星成像角度图
根据大小,所有的测绘区域可以分为2种类型:点目标和区域目标(regional target)。点目标可以由成像条带一次测绘完成覆盖,区域目标需要多个条带成像完成覆盖,因此,在做成像调度规划前,需要区域目标作处理。分解流程如图2所示,将区域目标分解成多个元任务(点目标),根据卫星星下点轨迹以及成像条带对全球区域进行栅格化分解,分解的最小单元能被成像条带一次成像覆盖,处理结果如图3所示。

图2 卫星成像波位扫描条带图
因此在单星调度问题中,每个测绘任务观测时间和观测波位的确定,成像卫星调度问题是对单轨内的测绘任务进行测绘先后选择和排序,同时需要满足卫星最大开关机次数、单轨最大成像时间、最短开机时间和波位切换时间等约束。
以往的研究是在固定时间内对测绘任务进行选择、排序,以求得最大测绘收益,本文将所有测绘任务排序,规划星载开关机时间和波位,求解测绘目标区域最小完成时间。

图3 区域目标划分结果图
1.2 调度模型

决策变量为:

目标函数:
(1)
约束条件:
(2)
(3)
ng≤g_onum
(4)
(5)
ifbcij=1andbj≠bi,wej≥bt+t_sta
(6)
(7)
(8)
其中,式(1)为目标函数,最小化完成所有测绘任务;约束(2)和(3)表示载荷一次开机时间有上下限;约束(4)为单轨卫星雷达载荷开关机次数有限;约束(5)表示单轨卫星雷达载荷最大成像总时间限制;约束(6)为载荷成像条带切换时间间隔约束;约束(7)为载荷关机重启时间间隔约束;约束(8)表示同一时间载荷只能一个成像条带开机测绘,测绘完成的任务不需要再次测绘。
2 改进蚁群算法
根据卫星调度问题的约束条件及目标函数,针对以上调度模型提出改进蚁群算法,由于基本蚁群算法搜索速度慢、易陷入局部最优解等缺点,因此本文借鉴蚁群系统和最大最小蚂蚁系统的思想设计寻优策略和信息素更新策略,即加入启发式搜索条件因素,在蚂蚁选择下一节点时给予额外的信息量;同时把每条边上的信息素限制在[τmin,τmax]区间内。
在求解该类问题时,测绘元任务类比蚂蚁所需经过的节点,测绘卫星类比蚂蚁,蚂蚁同一时间只能经过一个节点,即测绘卫星同一时间只能执行一个元任务,蚂蚁按照状态转移规则依次经过所有的节点,最终得到一条完整的路径,即得到测绘任务的执行序列。判断测绘任务执行序列的目标函数值更新信息素,以此反馈给蚂蚁下次的搜索过程。
2.1 寻优策略
蚂蚁从当前所在节点选择下一途径节点时,按照伪随机比例规则选择,当q≤q0:
pij={(τij)α(ηij)β(bij)γ}
(9)
j=maxj∈nextallow(ti){(τij)α(ηij)β(bij)γ}
(10)
其中,q为区间[0,1]均匀分布的随机数,q0为输入参数,当q≤q0时,按照式(11)的概率分布,通过轮盘赌注法选择一个随机变量。
(11)
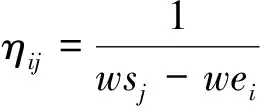
nextallow(ti)为任务ti下一个可以执行的任务,满足时间窗口不冲突、波位切换时间约束,同时需要满足最长开机时间约束。如果为空集,即没有满足条件的下一个测绘任务,有2种情况:1)当前轨道测绘任务安排结束,下一个执行任务未执行测绘任务中开始测绘时间最短的元任务,该元任务为下一轨道周期执行的第1个任务;2)卫星开机时间结束,需要关机,等待下一次开机时间,下一次开机时间需要满足星载重启时间约束。
2.2 信息素更新策略
当蚂蚁走过所有节点,即构造出可行的任务执行序列,得到完成所有测绘任务需要的轨道圈次数,比较当前轨道圈次g与全局最优轨道圈次gbest;若轨道圈次小于gbest,则更新全局最优解orderbest=order,gbest=g;为了加速收敛,只对每次循环中最优解执行序列上的信息浓度进行更新,更新规则如下:τij=(1-ρ)τij+Δτij
(12)
(13)
其中,ρ为信息素挥发率。
如果g>gbest,则对此次蚂蚁所经过路径上的信息素挥发
τij=(1-ρ)3τij
(14)
为了避免陷入局部最优解,当所有信息素更新结束后,对信息素进行判断控制:
如果τij≤τmin,则τij=τmin;
如果τij≥τmax,则τij=τmax。
2.3 算法流程
本文研究完成测绘任务的时间最短,因此,需要规划出测绘序列,尽可能在每轨测绘的任务数最多,这里选择开始测绘时间最小的任务作为每轨开始测绘任务。
步骤1:初始化各项参数α,β,γ,ρ0,Q;初始τij=τmin,迭代次数n=1;
步骤2:蚂蚁从当前开始时间最小的任务节点出发,开机时间为起始任务测绘开始时间,onoff=1,标记是否所有任务被排序执行;如果onoff=1,转步骤3;否则,转步骤10;
步骤3:判断onoff=1,若等于,寻找蚂蚁下一次可以经过的节点集合nextallow(ti),即未被安排执行的任务集合中,满足时间窗约束、波位切换约束、最长开机时间max_ont约束的测绘任务,并计算选择概率pij;若集合不为空,则转步骤4;否则,转步骤9;
步骤4:按照转移规则选择下一个任务,任务tj被选中,当前蚂蚁停在任务tj节点;判断当前星载是否开机,如果没有开机,转步骤5;否则,转步骤6;
步骤5:从未排序执行任务列表中删除任务tj,即将记录未安排任务数组中记录该任务序号的值计0,转步骤8;
步骤6:令开机次数onffnum加1,判断是否当前轨道开机次数小于单轨最大开机次数g_onum,如果是,开机时间为任务tj的wsj,转步骤5;否则,转步骤7;
步骤7:判断是否有未安排执行的测绘任务,若存在,令轨道数g加1,开机次数onffnum加1,从未安排的任务序列中选择开机时间最小的任务tl作为蚂蚁下一个途径的任务,开机时间为任务tl的wsj,转步骤5;
步骤8:统计已安排执行的任务数,如果所有的任务都安排执行了,令onoff=0;转步骤2;
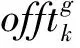
步骤10:得到测绘任务执行序列order,判断轨道圈次g是否小于最优轨道圈次gmin,如果是,最优执行序列order=orderbest;gmin=g;按照信息素更新策略,更新当前路径上的信息素
τij=(1-ρ)τij+Δτij
否则,挥发路径上的信息素。判断任务节点间的信息素,按照最大最小蚁群系统原则修改;
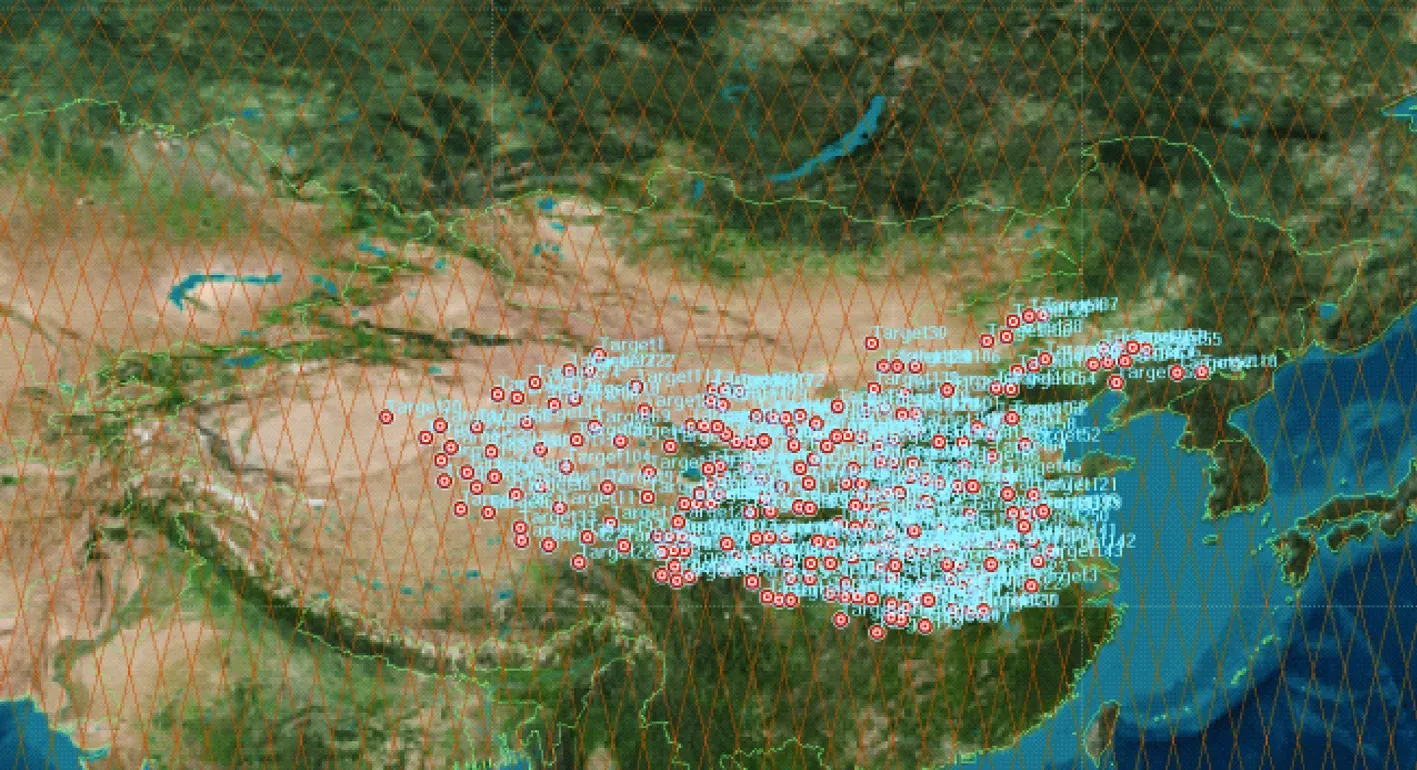
步骤11,若n 研究单星测绘任务时间最短调度问题,因此在卫星一个轨道测绘区域随机生成不同规模的目标数量,包括点目标和区域目标,对区域目标进行预处理,生成元任务。由于计算结果要与单轨最大化收益为目标结果作对比,定义任务的优先级为[0,1]之间的随机数。 仿真环境的参数如下: 1)卫星回归周期为15d,轨道数为227,卫星星下点轨迹以及测绘目标如图4; 2)成像条带的角度范围为 [19°,43°],12 个成像条带; 3)蚁群算法参数:最大迭代次数Nmax=600;α=1,β=2,γ=1,ρ0=0.02,Q=0.5。 图4 卫星星下点轨迹及测绘目标 图5 任务规模为500 图6 任务规模为600 图7 任务规模为800 分析仿真结果,图4是在任务规模为500时的对比图,可以看出在前8个周期中,目标函数为最大化收益时求解任务规划每个周期获得的收益大于以最小化时间为目标函数的,但是以时间为最小时,在第9个周期能将所有的任务测绘完,时间提升了25%。若用户提交的任务需要在10个周期内得到测绘结果,应采用以时间为目标函数进行任务规划求解;若用户提交的任务需要在5个周期内获得测绘结果,此时应以收益为目标进行任务规划求解。随着任务规模的增大,以时间为目标函数能使时间有显著提升,在任务规模为600时,最短完成测绘任务时间为11个周期,而以收益为目标函数时,需要14个回归周期,根据用户提交的任务需要可选择不同的方案。在任务规模为800时,可以看到在5个周期后,以时间为目标函数得到的收益优于以收益为目标函数的,同时在时间上有18.75%的提升,因此可以验证以时间为目标函数能够得到较好的结果,能针对用户递交的任务选择不同的任务规划方案。 针对应急测绘任务,以最小化完成测绘任务时间为优化目标,考虑了星载雷达成像的各种约束,建立测绘任务调度模型,改进蚁群算法对卫星测绘任务调度问题进行求解。为地面运管系统提供了一种新的成像策略优化目标,能够根据不同的测绘任务以及用户需求,选择不同的优化方案对实际卫星测绘做规划。今后的研究工作需要在以下几方面改进:考虑星载雷达测绘幅宽变化约束;加入星载数传约束条件;对算法进一步完善,解决多星成像任务调度问题,能够在较短时间内求解大规模测绘任务。 [1] 姜维,郝会成,李一军. 对地观测卫星任务规划问题研究述评[J].系统工程与电子技术,2013,35(9):1878-1885. (Jiang Wei, Hao Huicheng, Li Yijun. Review of Task Scheduling Research for the Earth Observing Satellites [J]. System Engineering and Electronics, 2013, 35(9): 1878-1885.) [2] Bensana E, Verfaillie G, Agnese, et al. Exact and Inexact Methods for The Daily Management of an Earth Observation Satellite [C]. Proceedings of the International Symposium on Space Mission Operations and Ground Data Systems. Munich, Germany, 2002, 507-514. [4] Jinbong Jang, Jiwoong Choi, Hee Jin Bae, et al. Image Collection Planning for Korea Multi-Purpose Satellite-2 [J]. European Journal of Operational Research,2013,230:190-199. [5] 贺仁杰,高鹏,白保存. 成像卫星任务规划模型、算法及应用[J].系统工程理论与实践, 2011, 31(3):411-422.(He R J, Gao P , Bai B C. Models, Algorithms and Applications to the Mission Planning Systems of Imaging Satellites [J]. Systems Engineering-Theory & Practice, 2011, 31(3): 411-422.) [6] 于海,郭玉华,李军. 一种卫星成像调度的约束修正方法[J].宇航学报,2008,29(4):1402-1407. (Yu Hai, Guo Yuhua, Li Jun. A Constraint Modification Approach for Imaging Scheduling of Earth Observing Satellites[J].Journal of Astronautics, 2008,29(4):1402-1407.) [7] 郝会成,姜维,李一军. 基于混合遗传算法的敏捷卫星任务规划求解[J].科学技术与工程, 2013,13(17):4972-4978. (Hao H C, Jiang W .Based on the Hybrid Genetic Algorithm of the Agile Satellite Mission Planning[J].Science Technology and Engineer 2013, 13(17):4972-4978.) [8] 靳肖闪,李军,等. 基于拉格朗日松弛与最大分支算法的卫星成像调度算法[J].宇航学报,2008,29(3):694-699.(Jin Xiaoshan, Li Jun, et al.An Algorithm for Satellite Imaging Scheduling Based on Lagrangian Relaxation and Max Weighted Component Algorithm[J]. Journal of Astronautics,2008,29(3):694-699.) [9] 冉承新,王慧林,熊纲要. 基于改进遗传算法的移动目标成像侦测任务规划问题研究[J]. 宇航学报,2010,31(2):457-465.(Ran Chengxin, Wang Huilin, Xiong Gangyao. Research on Mission-Planning of Ocean Moving Targets Imaging Reconnaissance Based on Improved Genetic Algorithm [J]. Journal of Astronautics, 2010, 31(2):457-465.) [10] 张帆,李军,王钧,等. 基于有效准则矢量生成的成像调度方法[J].航天控制,2005,23(6):81-84. (Zhang Fan, Li Jun, Wang Jun,et al. Imaging Scheduling Based on Efficient Criteria Vector Generation [J]. Aerospace Control, 2005, 23(6):81-84.) [11] Liu X L, Bai B C, Chen Y W. Multi Satellites Scheduling Algorithm Based on Task Merging Mechanism [J]. Applied Mathematics and Computation, 2014, 230: 687-700. [12] Hongrae Kim, Young Keun Chang. Mission Scheduling Optimization of SAR Satellite Constellation for Minimizing System Response Time [J]. Aerospace Science and Technology, 2015, 40:17-32. [13] Chen Y W, Yao F. A Learnable Ant Colony Optimization to the Mission Planning of Multiple Satellites [J].Systems Engineering-Theory & Practice, 2013, 33(3):791-801. Mission Scheduling Optimization Algorithm of Satellite for Minimizing Complete Imaging Task Time Zhang Zehao, Wang Jihe, Zhang Dexin, Shao Xiaowei School of Aeronautics and Astronautics,Shanghai Jiao Tong University,Shanghai 200240,China Aimingatsolvingthemissionplanningproblemofsatelliteimagingunderemergencyconditions,byconsideringtheconstraintssuchasswitchingtimeofimagingstripstoestablishschedulingmodel,theobjectiveconsideredisminimizedtocompleteimagingtasktimeinthispaper.Inaddition,animprovedantcolonyalgorithmisusedtosolvethisproblem.Anewoptimizationobjectiveisprovidedforgroundtransportationmanagementsystem,whichcanselectdifferentoptimizationschemesforsatelliteimagingaccordingtousers’requirements. Completeimagingtasktime;Antcolonyalgorithm;Scheduling;Emergency 2015-11-23 张泽浩(1992-),女,山西运城人,硕士,主要研究方向为卫星成像规划;王继河(1982-),男,黑龙江佳木斯人,博士,主要研究方向为编队/集群飞行构形设计与控制;张德新(1982-),男,江苏兴化人,博士,主要研究方向为分布式航天器系统仿真技术;邵晓巍(1974-),男,安徽肖市人,博士,副教授,主要研究方向为航天器导航与控制、系统仿真技术。 TP301.6 A 1006-3242(2016)04-0064-063 仿真实验分析




4 结论
