基于“当前”统计模型的后向迭代CKF算法研究*

吴博，刘鹏远，李宝晨

(军械工程学院,河北 石家庄　050003)



基于“当前”统计模型的后向迭代CKF算法研究*

吴博，刘鹏远，李宝晨

(军械工程学院,河北 石家庄050003)

摘要：针对机动目标的非线性跟踪问题，提出了基于“当前”统计模型的容积卡尔曼滤波(CS-CKF)。针对新算法对目标加速度阶跃机动跟踪延迟过大的问题，研究了后向迭代算法在估计精度和动态响应速度上的特点，提出了基于“当前”统计模型的后向迭代容积卡尔曼滤波算法。最后通过仿真实验比较了本文提出的CS-CKF算法和CKF算法的滤波效果。结果表明CS-CKF算法滤波效果优于CKF算法。

关键词：机动目标跟踪；非线性滤波；“当前”统计模型；容积卡尔曼滤波；后向迭代算法；动态特性

0引言

随着技术的进步及其在军事上的应用，空中目标的机动性大幅度提升使得目标跟踪系统动态性增强，而且雷达探测的双坐标体制使得量测方程存在非线性变换。因此，机动目标的非线性跟踪成了一个亟待解决的问题。

由于目标机动的不确定性，建立的目标模型与实际情况往往存在偏差。近年来，对机动目标建模问题的研究很多，提出了一些实用的模型。其中“当前”统计模型(current statistical，CS)[1-2]是在singer模型基础上的加速度均值自适应改进，其反映的目标机动变化更符合实际。量测方程的非线性处理方法主要有扩展卡尔曼滤波(EKF)[3-4]、无迹卡尔曼滤波(UKF)[5-6]、容积卡尔曼滤波(CKF)[7-8]。其中CKF能够避免EKF的高阶截断误差，同时其在高维系统的性能优于UKF[9-10]。

选取“当前”统计模型作为目标模型，采用CKF算法处理量测方程的非线性问题，提出了将两者相结合的基于“当前”统计模型的容积卡尔曼滤波算法(CS-CKF)。后向迭代算法通常用于对滤波过程的平滑以减小滤波方差，提高滤波精度。研究发现，后向迭代算法由于使用了当前时刻的状态估计进行二次滤波，使得系统的动态特性优于一般算法。为了解决CS-CKF在跟踪目标加速度阶跃机动时估计延迟较大的问题，引入后向迭代算法对原算法进行改进。Monte-Carlo仿真结果表明，新算法能够有效跟踪机动目标，其性能优于传统CKF算法。

1“当前”统计模型和容积卡尔曼滤波

1.1“当前”统计模型

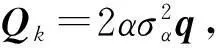
(1)

式中：amax，a-max为事先设定的加速度极限值。

1.2容积卡尔曼滤波

容积卡尔曼滤波算法是Ienkaran Arasaratnam和Simon Haykin在2009年提出的非线性滤波算法[11]。容积卡尔曼滤波利用根据三阶球面-相径容积规则选取容积点，将这些点经系统的非线性函数传递，再将传递后的点进行加权处理，用以近似状态后验均值和协方差。

考虑到如下非线性离散方程组：

Xk=f(Xk-1,Uk-1)+Wk-1，

Zk=h(Xk)+Vk，

(2)

式中：Xk和Zk表示状态向量和量测向量；Uk-1是输入矩阵；f(·)和h(·)为系统的状态函数和量测函数；系统噪声Wk-1是0均值方差为Qk的高斯白噪声；量测噪声Vk是0均值方差为Rk的高斯白噪声，Wk-1和Vk互不相关。

时间更新

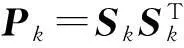
(3)

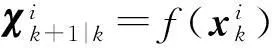
(4)

(5)

量测更新

(6)

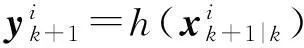
(7)

(8)

(9)

(10)

2基于“当前”统计模型的容积卡尔曼滤波

2.1状态方程

以二维空间定位为例，假设目标和观测站在同一水平面，观测的位置在坐标原点O(0,0)目标T从(xk,yk)处出发机动，rk表示观测站和目标的径向距离，θk表示观测站和目标连线与x轴的夹角，如图1所示。

图1　目标-观测站位置示意图Fig.1　Schematic diagram of target locationand observation station

通过“当前”机动模型建立目标的状态方程为

(11)

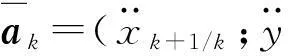
Xk+1=Φ0Xk+Wk,

(12)

式中：

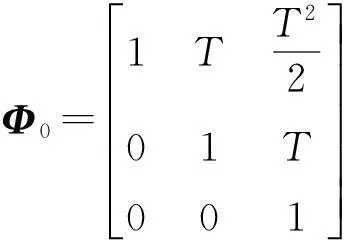
2.2量测方程

假设雷达只能测量目标的距离和方位角，根据图(1)中的几何关系可以得出

(13)

于是可以得到包括目标距离和方位角信息的量测方程[12-13]：

(14)

在CKF滤波过程中需要用式(12)代替式(4)，用式(14)代替式(7)，将当前统计模型计算得到的Qk带入式(5)，就得到基于“当前”机动模型的容积卡尔曼滤波算法。

2.3后向迭代算法

虽然CS-CKF能较好的跟踪上目标的状态，但是在仿真中可能出现对目标的加速度阶跃机动跟踪滞后，会导致滤波器的位置估计出现很大的偏差。为了解决这一问题，提高CS-CKF在目标加速度阶跃机动时的估计精度，文中引入了后向迭代算法对CS-CKF进行了改进，如图2所示。

通常经过一次滤波以后得到的结果已经可以消除大部分误差，故可以利用得到的当前时刻状态估计值与前时刻状态估计值进行后向处理，将得到的结果重新作为当前时刻的滤波初始值再次进行滤波[14-15]。这种后向迭代算法有2个优点：

(1) 第1次滤波已经滤除大部分误差，所以第2次滤波时得到的结果精度将优于第1次滤波的结果；

(2) 第2次迭代滤波的初始值中含有本时刻的量测信息和状态估计，所以系统的反应速度会比没有后向迭代的滤波算法快一个采样步长，能够有效改善系统的动态响应特性。

图2　后向迭代算法改进的CS-CKF流程图Fig.2　Flow chart of backward iterative improved CS-CKF algorithm

根据上文的理论分析，经过后向迭代算法改进后的CS-CKF算法流程为：

Step 1：根据2.1和2.2的描述进行第1次CS-CKF滤波，得到第1次k+1时刻的系统状态估计和系统误差协方差矩阵。

Step 2：结合k时刻系统状态估计和第1次滤波得到的k+1时刻系统状态估计，经过后向处理得到新的k时刻系统状态估计和系统系统误差协方差矩阵。

Step 3：将后向处理得到的新k时刻系统状态估计和误差协方差矩阵作为k+1时刻CS-CKF的滤波初始值，按照第1次滤波的计算流程进行第2次迭代滤波，得到新的k+1时刻系统状态估计和系统误差协方差矩阵作为滤波器的k+1时刻输出和下一时刻的滤波初值。

后向处理包括状态向量处理和误差协方差处理，其理论推导如下：

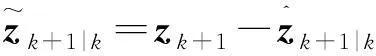
(15)

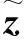
(16)

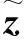
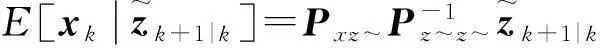
(17)

式中：

(18)

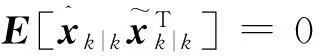
(19)

(20)

结合以上得到的结果代入式(16)得到状态的后向处理结果：

(21)

误差协方差矩阵的后向处理过程如下：

(22)

将式(22)移项得

(23)

用式(23)每一边的转置乘以自身可得

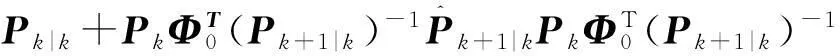
(24)

式中：

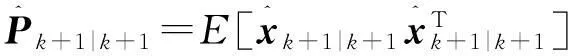
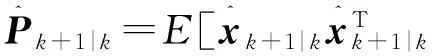
(25)

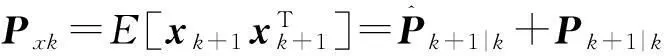
(26)

同理可以得到

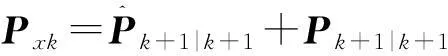
(27)

将式(26)和式(27)代入式(24)可得误差协方差的后向处理结果：

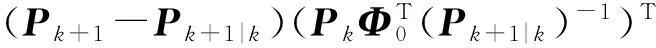
(28)

3仿真校验

为了检验新算法在动态特性上是否得到改善，进行了跟踪机动目标的仿真实验，并与传统CKF算法跟踪结果进行了比较，验证了新算法的有效性。

仿真实验条件：观测站固定于原点，起始位置和速度分别为(10，7)km和(20，20)m/s，目标在x方向上0～25 s做匀速直线运动，第25～50 s做加速度为5g的加速机动，50～125 s做匀速直线运动。观测角度上的噪声为0.003 rad，观测距离上的噪声为40 m。经过200次的Monte Carlo仿真CS-CKF算法和CKF算法的性能比较如图3所示。

通过图3中的数据比较可以看出，当目标加速度保持不变时，CKF和CS-CKF的跟踪性能相近。当目标发生加速度阶跃机动时，图3a)显示CS-CKF算法响应比CKF算法快1～2个采样步长，反应在速度误差上则表现为动态误差较小，收敛速度更快。图3c)，3d)2图中，CKF在机动时间点后观察距离和角度误差出现了2个明显的峰值；CS-CKF算法在同样的时间点处虽然误差有所增大，但是与整体误差水平相差不大，说明CS-CKF算法在距离和角度上明显优于CKF算法。

表1中的数据显示，CS-CKF算法跟踪加速度、速度、距离以及角度的误差方差都要小于CKF算法，这说明CS-CKF算法的滤波结果更加平滑；CS-CKF算法距离误差和角度误差的最大值明显小于CKF的误差最值，说明CS-CKF的动态响应速度更快，能更好地跟踪目标机动。

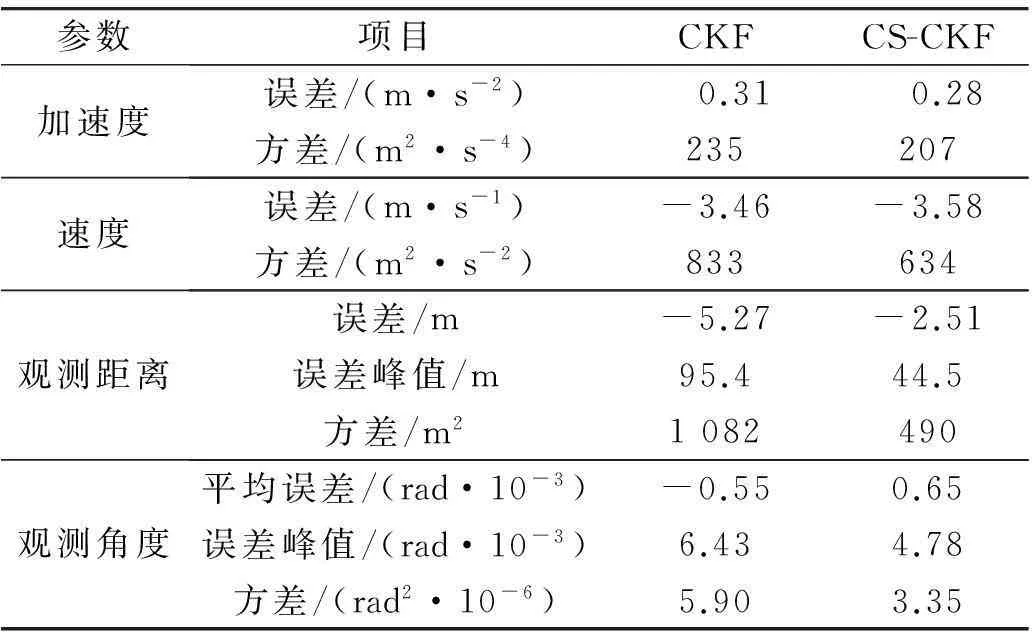
表1　CKF与CS-CKF对加速度阶跃机动的跟踪效果比较

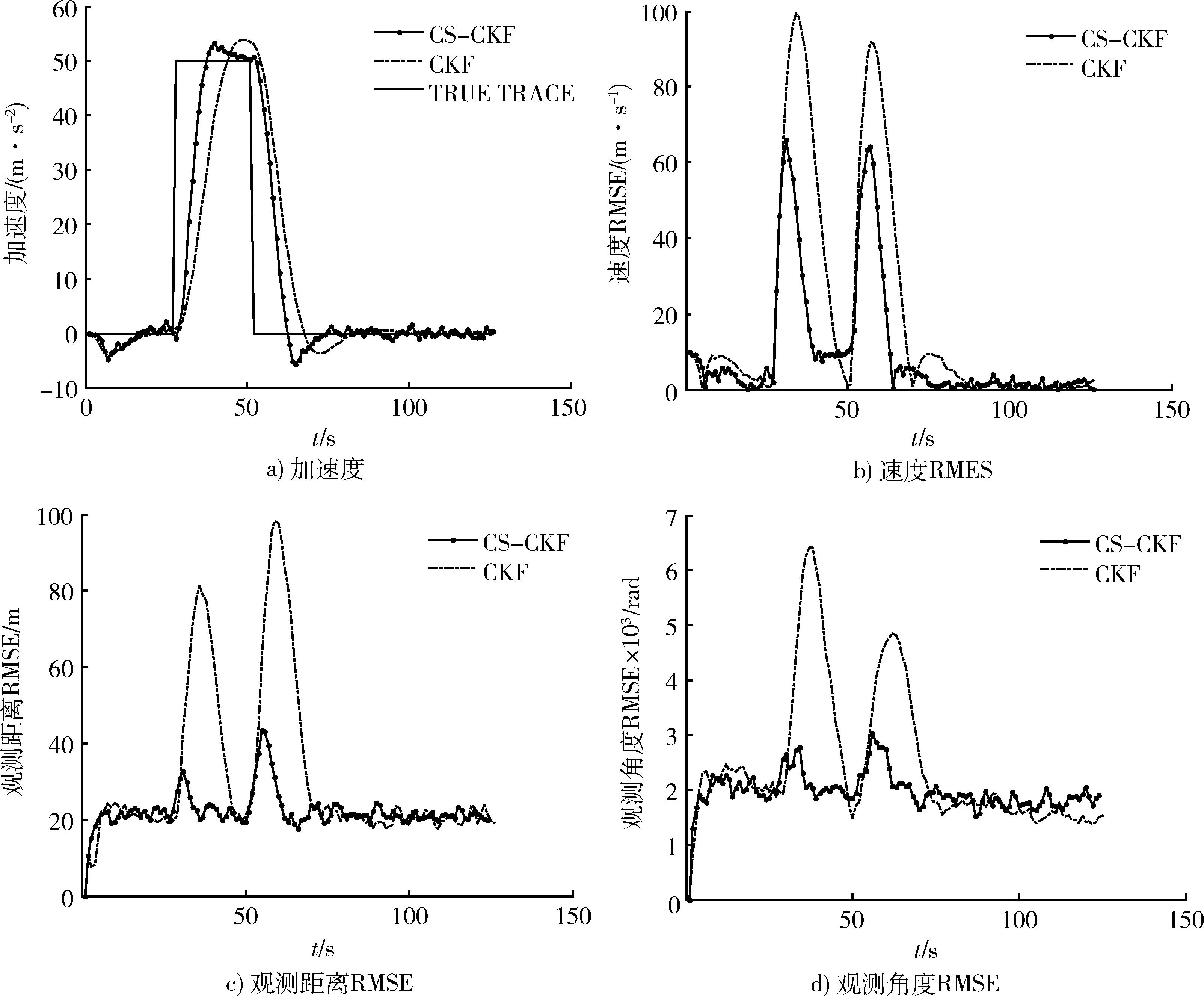
图3　CKF与CS-CKF对加速度阶跃机动的跟踪效果比较Fig.3　Comparison between CKF and CS-CKF tracking targets with step acceleration maneuver

4结束语

为了得到对机动目标跟踪精度更高的非线性滤波器，提出了基于“当前”统计模型和容积卡尔曼滤波算法。针对新算法对加速度阶跃机动存在较大延迟的问题，研究了后向迭代算法在滤波精度和动态响应速度上的优点，并将后向迭代算法应用于CS-CKF算法的改进，最终得到了基于“当前”统计模型的后向迭代容积卡尔曼滤波器。通过跟踪进行加速度阶跃的机动目标轨迹，对常规CKF和本文提出的CS-CKF的滤波效果进行了比较。仿真实验结果表明，本文提出的CS-CKF算法能够有效跟踪目标加速度阶跃机动轨迹，并且在动态响应速度和跟踪精度上优于传统的CKF算法。

参考文献：

[1]徐洋,徐松涛,赵建恒，等. 基于“当前”统计模型的机动目标自适应跟踪算法[J]. 现代防御技术, 2014, 42(5):121-125.

XU Yang, XU Song-tao, ZHAO Jian-heng et al. Based on the “Current” Statistical Model Aadaptive Maneuvering Target Tracking Algorithm [J]. Modern Defense Technology, 2014, 42(5) : 121-125.

[2]钱华明,陈亮,满国晶,等.基于当前统计模型的机动目标自适应跟踪算法[J].系统工程与电子技术, 2011, 33(10) : 2154-2158.

QIAN Hua-ming, CHEN Liang, MAN Guo-jing, et al. Tracking Algorithm for Adaptive Maneuvering Target Based on Current Statistical Model[J]. Systems and Electronics Engineering, 2011, 33 (10): 2154-2158.

[3]张蕊,史丽楠. 基于扩展卡尔曼滤波的机动目标跟踪研究[J]. 航天控制, 2012, 30(3):12-18.

ZHANG Rui, SHI Li-nan. Study of Maneuvering Target Tracking Based on Extended Kalman Filter[J]. Aerospace Control, 2012, 30(3):12-18.

[4]孙杰,胡瑞,杨辉. 基于改进扩展卡尔曼滤波算法的空中目标跟踪[J].舰船电子对抗,2013,36(6):34-37.

SUN Jie, HU Rui, YANG Hui. Air Target Tracking Based on Improved Extended Kalman Filtering Algorithm [J]. Journal of Ship Electronic Countermeasures, 2013, 36 (6):34-37.

[5]唐浩. UKF应用于制导系统[J]. 现代防御技术,2010,38(6):66-69．

TANG Hao. UKF is Applied to the Guidance System [J]. Modern Defense Technology, 2010, 38(6):66-69.

[6]陈洪,李晶,张茂辉,等. 基于IMM-UKF的航天测控雷达机动目标跟踪[J]. 现代电子技术,2014,37(13):43-46.

CHEN Hong, LI Jing, ZHANG Mao-hui， et al. Aerospace TT&C Radar Maneuvering Target Tracking Based on IMM-UKF [J]. Modern Electronic Technology, 2014,37(13):43-46.

[7]葛磊.容积卡尔曼滤波算法研究及其在导航中的应用[D].哈尔滨：哈尔滨工程大学，2012.

GE Lei. Volume Kalman Filter Algorithm and Its Application in the Navigation [D]. Harbin: Harbin Engineering University, 2012.

[8]鹿传国,冯新喜,张迪. 基于改进容积卡尔曼滤波的纯方位目标跟踪[J]. 系统工程与电子技术, 2012, 34(1):28-33.

LU Chuan-guo, FENG Xin-xi, ZHANG Di. Pure Bearing Target Tracking Based on Improved Cubature Kalman Filter [J]. Systems Engineering and Electronics, 2012, 34(1) : 28-33.

[9]穆静,蔡远利. 迭代容积卡尔曼滤波算法及其应用[J].系统工程与电子技术,2011,33(7):1454-1457.

MU Jing, CAI Yuan-li. Iterative Volume Kalman Filter Algorithm and Its Application [J]. Systems Engineering and Electronics, 2011,33 (7) : 1454-1457.

[10]孙枫,唐李军. Cubature卡尔曼滤波与Unscented卡尔曼滤波估计精度比较[J].控制与决策,2013,28(2):303-308.

SUN Feng, TANG Li-jun. Cubature Kalman Filtering with the Unscented Kalman Filter Estimation Precision Comparison [J]. Control and Decision, 2013, 28 (2):303-308.

[11]Ienkaran Arasaratnam, Simon Haykin. Cubature Kalman Filters[J]. IEEE Trans on Automatic Control, 2009, 54(6): 1254-1269.

[12]张洋,芮国胜,苗俊,等.扩展容积卡尔曼滤波定位技术研究[J].光电工程,2012, 39(4):37-42.

ZHANG Yang, RIN Guo-sheng, MIAO Jun, et al. Expanded Cubature Kalman Filter Positioning Technology Research [J]. Journal of Electrical Engineering, 2012, 39(4):37-42.

[13]霍光,李冬海. 基于CKF的单站无源定位跟踪算法[J].指挥信息系统与技术，2013,4(1):17-20.

HUO Guang, LI Dong-hai. Algorithm of Single Observer Passive Location and Tracking Based on CKF[J]. Command Information System，2013, 4 (1): 17-20.

[14]曹意,茅旭初. 基于非线性滤波和平滑相迭代的GPS定位估计算法[J].上海交通大学学报,2009,43(7):1108-1112．

CAO Yi, MAO Xu-chu. Estimation Algorithm Based on GPS Nonlinear Filtering and Smoothing Phase Iteration[J]. Journal of Shanghai Jiaotong University, 2009, 43(7):1108-1112.

[15]Ienkaran Arasaratnam, Simon Haykin. Cubature Kalman Smoothers [J].Automatica, 2011,47:2245-2250.

Backward Iterative Improved Cubature Kalman Filter Based on Current Statistical Model

WU Bo，LIU Peng-yuan，LI Bao-chen

(Ordnance Engineering College,Hebei Shijiazhuang 050003,China)

Abstract:In order to solve the problem of nonlinear maneuvering target tracking, a new cubature Kalman filter based on “current” statistical model (CS-CKF) is studied. According to the problem of excessive delay on the step acceleration maneuvering during target tracking, a backward iterative algorithm that amends the last state estimation with the predicted current state is analyzed and applied for improving. Finally, the two kinds of typical maneuvering models are applied to CKF and CS-CKF, and the effects of the two algorithms are compared. The simulation results show that CS-CKF algorithm is better than the CKF algorithm.

Key words:maneuverable target tracking; nonlinear filtering; “current” statistical model; cubature Kalman filter; backward iterative algorithm; dynamic characteristics

*收稿日期：2015-04-20；修回日期：2015-07-07

作者简介：吴博(1990-)，男，福建漳州人。硕士生，主要研究领域为武器系统建模与仿真。

通信地址：050003河北省石家庄市和平西路97号4系中程防空导弹教研室E-mail：bluegd@qq.com

doi:10.3969/j.issn.1009-086x.2016.03.007

中图分类号：TJ765；TP391.9

文献标志码：A

文章编号：1009-086X(2016)-03-0038-06

导航、制导与控制