考虑目标机动及修正动力学的最优制导律研究

张文渊 郭 涛 夏群利 温求遒

1. 北京理工大学宇航学院，北京100081 2. 北京航天自动控制研究所，北京100854



考虑目标机动及修正动力学的最优制导律研究

张文渊1郭 涛2夏群利1温求遒1

1. 北京理工大学宇航学院，北京100081 2. 北京航天自动控制研究所，北京100854

以实现对机动目标的精确打击为背景，首先基于目标常值指令机动模型，同时考虑目标机动动力学、导弹制导动力学及重力影响，采用Schwartz不等式法推导得到了一种贴近工程应用的改进最优制导律(Improved Optimal Guidance Law)，然后对该制导律的加速度指令特性与制导脱靶量进行了分析。仿真结果表明，改进最优制导律的加速度指令在大部分末导时间内都小于其他制导律，在末端攻击时刻其加速度指令接近零值。其制导脱靶量不受目标机动和末导时间的影响，始终保持在零值附近，该制导律对机动目标的攻击具有较好的性能优势。

目标机动；制导动力学；最优制导律

为提高复杂战场环境下的生存概率和突防效率，出现了越来越多具有大机动性能的目标，目标的高机动性会大幅降低导弹攻击的成功率，因此实现对机动目标的精确打击已成为当前战略战术武器发展的必然要求。

导引律是实现导弹对机动目标精确打击的重要依据，比例导引律PNG (Proportional Navigation Guidance Law)是较为传统和应用最广泛的一种制导律，它被证明是目标不机动以及系统零滞后情况时的最优制导律[1-2]。但对大机动目标来说，比例导引律由于末端需用过载过大导致其性能已难以满足末端拦截的需求[3]。增强比例导引律APN(Augmented Proportional Navigation)引入了对常值机动目标的补偿，相比比例导引律PNG，增强比例导引律APN可减小末端需用过载，被证明是在系统理想情况下对付常值机动目标的最优制导律[4-5]。而真实的导弹系统存在诸多动力学，动力学滞后导致PNG和APN制导律都会有比较大的末端过载需求，并产生较大的脱靶量[6]。考虑目标常值机动的情况下，将导弹制导动力学简化为一阶滞后模型，可推导出OPN(Optimal Proportional Navigation)最优制导律[7-8]，该制导律可较好地消除导弹制导动力学影响。但事实上目标机动也存在动力学，更真实的情况是目标为有动力学常值加速度指令的机动[9-10]，目前很少有制导律关注这种目标机动形式，这导致当前制导律与实际情况不匹配，未能有效减小导弹需用过载能力以实现更有效的拦截。

本文基于目标为有动力学滞后系统，并采用常值加速度指令机动方式，同时考虑导弹制导系统动力学及重力影响，采用Schwartz不等式法推导得到了一种贴近工程应用的改进最优制导律(Improved Optimal Guidance Law)，然后对该制导律的加速度指令特性与制导脱靶量进行了仿真分析，通过与比例导引律PNG和增强比例导引律APN进行对比，验证了改进最优制导律在攻击机动目标时的有效性和最优性。

1 问题描述

改进最优制导律在推导之前建立如下假设条件：1)采用二维平面交战模型，本文导弹和目标均在纵向平面运动；2)导弹和目标均为质点运动模型；3)导弹和目标的末端交战弹道沿参考线(初始基准线)是线性的；4)导弹制导系统为一阶动力学滞后系统。

1.1 目标机动模型

在实际工程应用中，对目标机动状态估计的准确性是影响最优制导律最优性的主要因素，目标机动估计模型与实际模型越接近，则推导出的最优制导律越具有最优特性和工程应用价值。本文以目标为有动力学滞后系统并采用常值加速度指令机动方式为模型[10]，假设目标为一阶动力学系统，包含动力学时间常数Tt和噪声，该机动模型表达式如下：

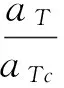
(1)

对于常值机动指令，目标机动模型数学表达式如下：

(2)

式中，aT为目标机动实际加速度；aTc为目标机动加速度指令；ω为白噪声，代表目标机动的不确定性，此处ω取零值。

1.2 系统模型

图1给出了弹目拦截几何关系，LOS为基准弹目线，XOY为惯性坐标系，yM和yT为相对XOY惯性坐标系垂直于LOS基准弹目线方向的导弹和目标位置，y为相对位置，aM和aT为导弹和目标垂直于基准线方向的绝对加速度，其中，λ为弹目视线角，vT为目标速度，vM为导弹速度。

图1 拦截几何关系

图2 系统状态模型

图2给出了系统状态模型，其中，Tg为导弹制导动力学时间常数，根据图2可得系统状态空间表达式为：

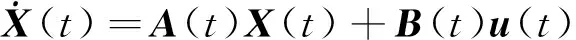
(3)

式中，X(t)为系统状态量，A(t)为状态矩阵，B(t)为控制矩阵，u(t)为控制量。通过前文的分析可知，该系统状态量X(t)应包含弹目相对位置和速度，目标机动加速度和加速度指令，导弹过载指令以及重力补偿项，控制量u(t)为导弹加速度指令amc。

其中，

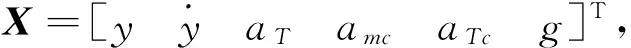
(4)

2 改进最优制导律推导与应用

2.1 制导律推导

在改进最优制导律求解时，以末端零脱靶量及最小过程控制能量为约束，可把目标函数写为：

(5)

式中，下标f代表末端状态量，考虑本文弹目拦截情况，状态矩阵取如下形式：

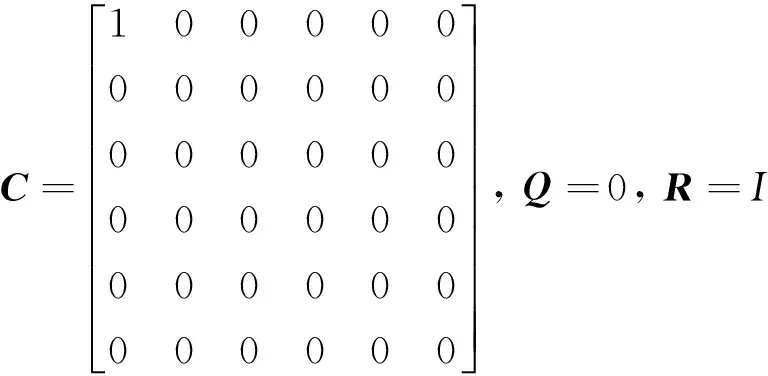
(6)

上述问题是一个最优控制问题，求解该问题时可采用最优控制求解方法，也可采用Schwartz不等式求解，本文采用Schwartz不等式法求解最优制导律，以保证下式成立，

(7)

状态方程式(3)在tf处的解可表示为：

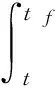
(8)

式(8)中状态量的基础转移矩阵为：

Φ(t)=L-1[(sI-A)-1]

(9)

式中，I为单位矩阵，s为复频域的符号，L-1为拉普拉斯反变换。式(8)也可表示为式(10)形式：

(10)

式中,Ti=tf-t。

式(8)中第1个状态量y在终端可表示为：

(11)

式中，

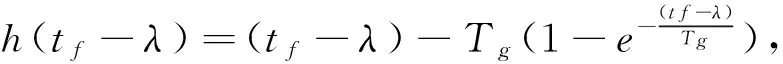
(12)

将终端条件y(tf)=0代入式(11)中，可得：

(13)

对式(13)应用Schwartz不等式有：

(14)

当且仅当等号成立时，所需能量最小，因此可推出改进最优制导律表达式为：

(15)

进一步，可以把改进最优制导律写成便于工程应用的形式：

(16)

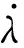
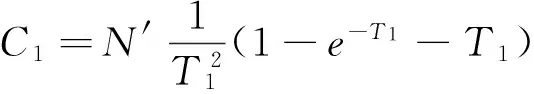
由式(16)可知，改进最优制导律的第1项类似于比例导引律PNG，为制导律的主项，第2项是对导弹制导动力学的修正项，第3项和第4项是对目标机动加速度和加速度指令的修正项，最后一项是对重力加速度的修正项。

2.2 制导律应用

在实际应用改进最优制导律时，以采用雷达导引头的导弹为例，制导律所需制导信息获取方式如下：

2)导弹加速度aM可由弹上加速度计测量获取；

3)导弹制导动力学时间常数Tg为设计参数，视为已知量；

4)目标机动动力学时间常数Tt可通过对典型机动目标动力学特性进行统计，提前装订于弹上计算机，实际使用时根据当前目标特性选取合适的参数；

5)剩余飞行时间tgo由简化公式tgo=R/Vr计算得到，其中弹目相对距离R由雷达导引头测得；

6)目标机动加速度aT和加速度指令aTc可采用卡尔曼滤波器方程估计得到，具体方法如下。

根据图2得到目标机动的卡尔曼滤波器状态方程和量测方程为：

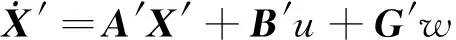
(17)

Z=C′X′+v

(18)

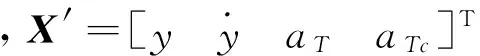
(19)

式中,状态转移矩阵Φk=Φ(Ts)，Ts为离散步长。

利用Ricatti方程递推解出迭代方程为：

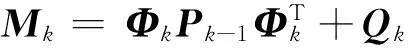
(20)

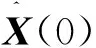
(21)

3 改进最优制导律特性分析

根据式(16)及文献[1-5]可给出改进最优制导律与比例导引律、增强比例导引律表达式的区别，如表1所示。

从表1可以看出，相比于比例导引律和增强比例导引律，改进最优制导律受目标机动及目标机动动力学与导弹制导动力学的影响，应具有更好的制导效果，下面通过仿真来分析改进最优制导律的制导特性。表2给出了制导律仿真初始条件。

表1 不同制导律表达式

表2 仿真初始制导参数

图3给出了改进最优制导律制导系统框图，利用图3仿真得到制导律加速度指令随末导时间变化曲线，如图4所示。仿真结果可以看出，改进最优制导律的加速度指令随着末导时间增加而减小，在弹目交汇处，比例导引律与增强比例导引律存在较大的加速度指令，会造成由于指令饱和而产生脱靶的情况，而改进最优制导律指令较小且趋近于零值，此时小指令有利于对目标的截获。

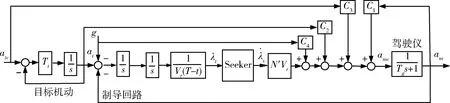
图3 改进最优制导律制导系统框图

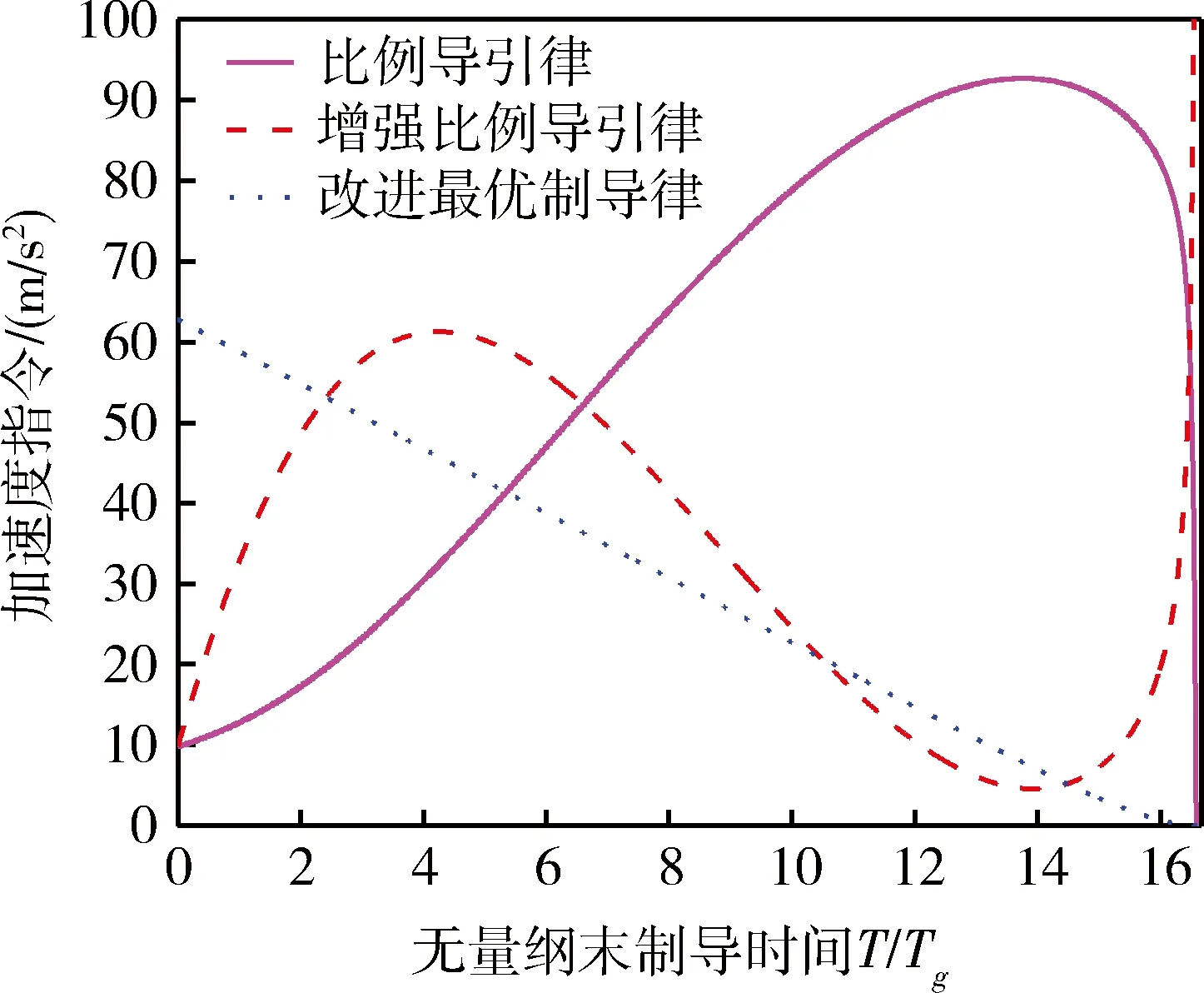
图4 加速度指令随末导时间变化曲线

进一步为了分析制导脱靶量对于目标机动的敏感性，采用伴随函数法将图3进行伴随变换，得到图5所示伴随系统。利用伴随系统可仿真得到当目标有3g加速度指令时，引起的3种制导律制导脱靶量随末导时间的变化曲线，如图6所示。由于目标机动和导弹制导动力学的影响，比例导引律与增强比例导引律需要较大的末导时间消除制导脱靶量，当制导系统有大于16倍的相对末导时间(T/Tg)时，脱靶量才出现收敛到零值的趋势。而改进最优制导律脱靶量不受末导时间限制，始终保持零值。

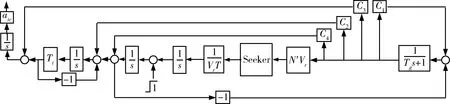
图5 改进最优制导律伴随系统框图

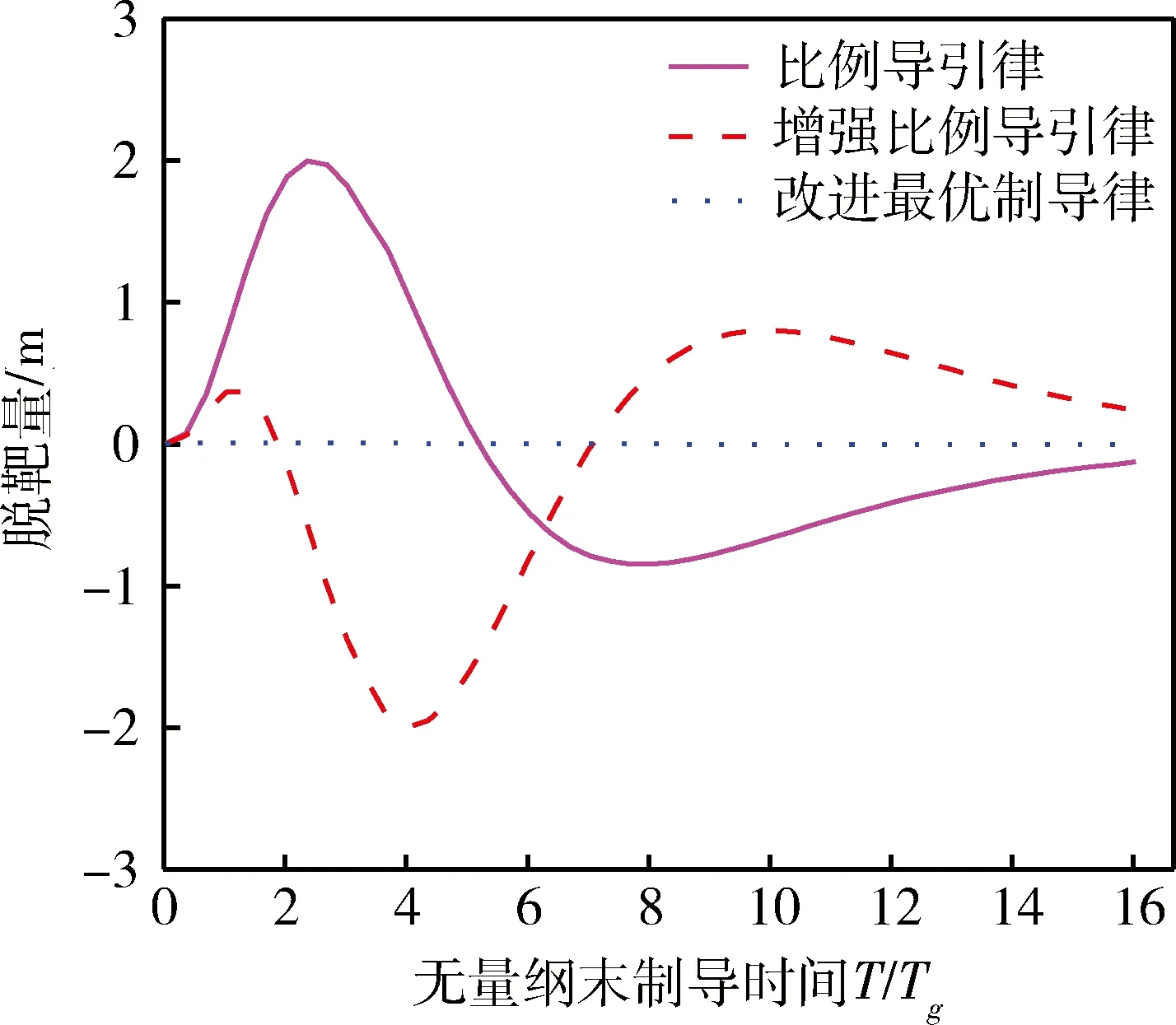
图6 目标机动引起的制导脱靶量随末导时间变化曲线

4 总结

以实现对机动目标的精确打击为背景，基于目标常值指令机动模型，同时考虑目标机动动力学、导弹制导系统动力学及重力影响，推导得到了一种贴近工程应用的改进最优制导律，相比于比例导引律与增强比例导引律，该制导律具有较小的加速度指令需求和制导脱靶量，其制导脱靶量不受目标机动和末导时间的影响，验证了改进最优制导律对机动目标的攻击具有较好的性能优势。本文研究成果将对机动目标打击和最优制导律研究提供了一定的理论支撑。

[1]ZarchanP.TacticalandStrategicMissileGuidance(SixthEdition) [M].AIAA:ProgressinAstronauticsandAeronautics, 2012.

[2]ShneydorM.AQualitativeStudyofProportionalNavigation[J].IEEETransactionsonAerospaceandElectronicSystems, 1994, 30(1): 637-643.

[3]GilbertT.Tso,RobertN.Lobbia.MultimodeguidanceinAdvancedAir-to-airMissileApplications[C]//AIAAGuidanceNavigationandControlConference, 1986.

[4]BabuKR,SarnlatIG,SwamyKN.TwoVariable-StructureHomingGuidanceShemesWithandWithoutTargetManeuverEstimation[C]//AIAAGuidanceNavigationandControlConference,AZ. 1994: 216-225.

[5]BobergB,LundbergJ,WibergJ,etal.Estimationoftargetlateralaccelerationforaugmentedproportionalnavigation[C]//AIAAConferenceonGuidance,NavigationandControl. 1977: 11-13.

[6]VincentTL,CottrellRG,MorganRW.Minimizingmaneuveradvantagerequirementsforahit-to-killinterceptor[C]//Proc.oftheAIAAGuidance,NavigationandControlConferenceandExhibit, 2001: 1-11.

[7]ZarchanP,GreenbergE,AlpertJ.Improvingthehighaltitudeperformanceoftail-controlledendoatmosphericmissiles[C]//AIAAGuidance,NavigationandControlConferenceandExhibit, 2002: 4770-4780.

[8]GurfilP.Zero-miss-distanceguidancelawbasedonline-of-sightratemeasurementonly[J].ControlEngineeringPractice, 2003, 11(7): 819-832.

[9]HexnerG.Apracticalstochasticoptimalguidancelawforboundedaccelerationmissile[J].JournalofGuidance,ControlandDynamics, 2011, 34(2): 437-445.

[10]HexnerG,WeissH.Temporalmultiplemodelestimatorforamaneuveringtarget[J].AIAAPaper, 2008: 7456.

The Study of Optimal Guidance Law Based on Target Maneuver and Modificatory Dynamics

Zhang Wenyuan1, Guo Tao2, Xia Qunli1, Wen Qiuqiu1

1. Beijing Institute of Technology, School of Aerospace Engineering, Beijing 100081, China 2. Beijing Aerospace Automatic Control Institute, Beijing 100854, China

Aimingattheprecisionattackofmaneuveringtarget,firstly,basedonthetargetstepmaneuveringmode,theSchwartzmethodisusedtoderiveanimprovedoptimalguidancelaw,whichisbasedonthetargetstepmaneuveringmode.Thetargetmaneuverdynamicsandacceleration,guidancesystemdynamicandgravityaccelerationareconsideredanddynamicallycancelledouttheireffectsinguidancelaw.Andthenthestudyofoptimalguidancelaw’saccelerationcommandandguidancemissdistanceisimplemented.Thesimulationresultsshowthelessmissileaccelerationisrequiredinmosttimeofguidanceespeciallyattheendofinterceptbyusingtheoptiamalguidancelawwhichislesssensitivetoerrorscausedbytargetmaneuveringandmissiletime-to-go.Theguidancelawshowssignificantperformancesuperioritywhenmaneuveringtargetisattacked.

Targetmaneuver;Guidancesystemdynamics;Optimalguidancelaw

2013-08-17

张文渊(1987-)，男，陕西蒲城人，博士研究生，主要研究方向为高超声速飞行器制导与控制技术；郭 涛(1983-)，男，山东临朐人，博士，工程师，主要研究方向为飞行器总体设计；夏群利(1971-)，男，辽宁抚顺人，博士，副教授，主要研究方向为飞行器总体设计，飞行器制导与控制；温求遒(1982-)，男，桂林人，博士，讲师，主要研究方向为飞行器制导与控制技术。

V448.23

A

1006-3242(2016)03-0008-06