基于混沌占空置乱和DNA编码的图像加密算法

王光义　任国瑞　崔明章　蔡博振

(杭州电子科技大学电子信息学院　浙江 杭州 310018)



基于混沌占空置乱和DNA编码的图像加密算法

王光义任国瑞崔明章蔡博振

(杭州电子科技大学电子信息学院浙江 杭州 310018)

摘要为了增强加密图像的安全性，提出一种新的基于混沌占空置乱和DNA编码的图像加密算法。首先根据一种离散混沌映射产生的伪随机序列使用占空法对图像矩阵的行和列进行随机交换，相比一般的混沌置乱大大提高了运算速度。然后利用另一种离散混沌映射产生两个伪随机序列分别对图像矩阵的前n行像素点和其余像素点进行异或运算生成加密图像。最后利用DNA编码规则，对图像矩阵中像素点灰度值的每两位二进制位分别进行对应的互补替换，达到图像扩散的目的，最终生成加密后的图像。对算法的统计特性、密钥敏感性及密钥空间进行仿真验证与分析，对算法的复杂性进行理论分析，分析结果显示该算法具有较高的安全性。

关键词混沌占空置乱DNA编码图像加密安全性分析

0引言

随着近几年互联网技术的飞速发展，人们的生活已经与互联网密切相关，大量个人或企业图像信息被存放在网络上，或开始在网络中传输，然而这些图像都存在着一定的安全隐患。于是对图像进行加密处理开始变得十分关键。由于传统加密算法如DES、AES、IDEA等，并没有考虑图像格式的特点，另外，数据量大、冗余度高和像素的相关性强等，所以不再适合应用于图像加密。而当前广泛使用的基于图像像素点置乱的图像加密技术，如Arnold变换[1]、Hilbert曲线变换[2]、矩阵变换[3]等，均具有周期性，且无法改变图像的灰度直方图特性，安全性相对较低。

近年来许多学者开始对混沌应用于加密技术越来越感兴趣，人们发现混沌对初始值的敏感性、伪随机性、统计学和拓扑学等特性，非常适合应用于加密系统。因此将置乱与混沌系统相结合应用于图像加密正成为热点。文献[4]将Arnold变换和扩散函数相结合来对数字图像进行置乱加密，虽然解决了Arnold变换无法改变图像灰度直方图特性的缺陷，但其算法相对简单，安全性不高。文献[5]将图像进行DNA编码后分为4个子图像，并利用Logistic混沌序列分别对每个子图像置乱加密，但此算法密钥空间小，无法抵抗穷举攻击。文献[6-8]将DNA编码与混沌系统相融合应用于图像加密，DNA编码由于继承了遗传分子的并行性和高信息密度等特性[11]，现今被广泛应用于加密系统[6]。而混沌系统与DNA编码相结合也成为了研究的热点。

为了解决普通置乱方法中置乱序列的周期性和无法改变图像灰度直方图特性的问题，本文利用混沌伪随机序列来控制图像矩阵中像素点位置的交换，然后利用另一种混沌序列对置乱后图像加密。基于DNA编码应用于加密系统的巨大优势，本文同时将DNA编码引入加密系统，提出一种基于混沌占空置乱和DNA编码的图像加密算法。首先使用改进型logistic映射产生图像置乱所需的混沌序列，利用另一种性能良好的改进型Tent映射产生对图像异或运算所需的混沌序列，利用DNA编码规则对图像像素点进行扩散，最终生成加密后的图像。安全性分析显示该方法具有良好的加密特性。

1混沌系统及DNA编码

1.1改进型Logistic映射

改进型Logistic映射表达式[9]：

(1)

式(1)改进型Logistic序列xn∈(-1.2,1.2)，相比于原来的Logistic序列迭代范围(0,1)扩大了许多。系统在(2.35,3)区间处于混沌态，相比原来序列密钥空间更大，且改进型的Logistic映射的Lyapunov指数最大值为1.041左右。而Logistic映射的Lyapunov指数最大为0.667，说明改进型系统对初始值更加敏感，序列的随机性更好。本文将其产生的混沌序列应用于图像置乱。

1.2改进型Tent映射

改进型Tent映射表达式[10]：

(2)

式(2)中μ∈(1,2)时，系统处于混沌状态，改进型系统迭代范围为(0,k)，其中k>1，相比于原来的区间(0,1)迭代范围有了明显的扩展。

1.3DNA编码

本文采用DNA编码理论对像素位置被置乱并加密处理后的图像进行编码。将每一个像素用8位二进制表示，每2位用一个DNA碱基(A,G,C,T)表示。由此可得出8种编码规则[11]，如表1所示。

表1　DNA编码规则

根据碱基互补原则，可以得到6种碱基对，如表2所示。

表2　碱基互补规则

2基于混沌占空置乱和DNA编码的图像加密算法

2.1加密算法

首先利用混沌占空置乱的方法对图像进行置乱。然后利用另一种性能良好的混沌系统产生两个混沌序列分别对置乱图像前n行像素点和其余像素点进行异或运算生成加密图像。最后利用DNA编码规则，对图像矩阵中像素点灰度值的每两位二进制位分别进行对应的互补替换，达到图像扩散的目的，最终生成加密后的图像。

所谓混沌占空置乱，是指利用混沌序列对图像矩阵中行(列)像素点的位置进行交换。假设原始图像G0大小为M×N，其行向量为G0(i)，i∈(1,M)，像素点值为G0(i,j)∈(0,255)，i∈(1,M),j∈(1,N),x(i)为映射到(0, 255)的一维离散混沌序列。

首先将原始图像G0初始化为所有像素点值为0的图像矩阵G1，且G1的行向量为G1(i),像素点值为G1(i,j)∈(0,255),则混沌占空行置乱的数学表达式为：

(3)

式中，G0代表原始图像矩阵，即明文；G1代表置乱后的图像矩阵；[x(i)]表示对序列x(i)取整。ROR(X)表示在1-M中查找满足G1(f(X),0)=0的X值。

混沌占空列置乱，原理同行置乱。

2.2图像加密与解密

图像加密的流程如图1所示。

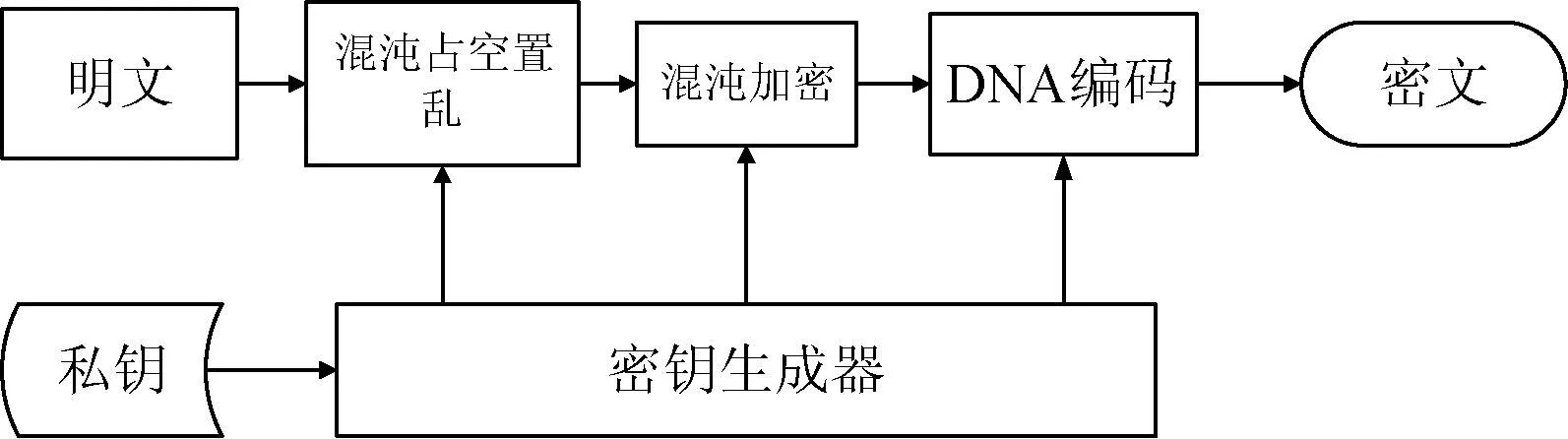
图1　加密算法流程图

图像加密算法的步骤如下：

步骤1将灰度图像转化为大小为M×N的二维矩阵G，灰度值为0～255。

步骤2改进型Logistic映射的初值a0，参数μa。生成离散一维的混沌序列La，然后将La映射到0～255之间，根据其位置编号与值的关系，交换矩阵G的行和列，从而得到置乱后的图像G2。

具体算法如下：

(1) 原始图像的行号如表3所示。

表3　原始图像行号

(2) 行置乱的方法如下：

混沌序列及量化结果如表4所示。

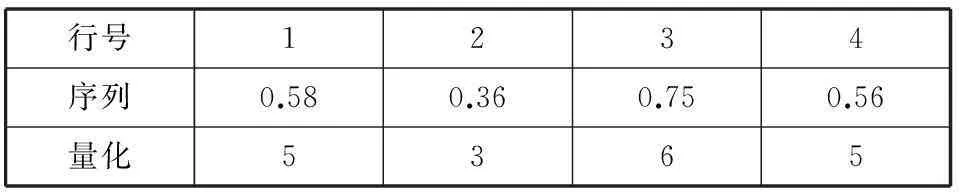
表4　混沌序列及量化结果

续表4

备注：量化公式为ceil(x×M)。

占位结果如表5所示。

表5　占位结果

说明：根据第1步的量化结果，0.58量化为5，所以将行号为1的所有像素点放在第5行的位置；0.36量化结果为3，所以将行号为2的所有像素点放到第3行的位置。依次类推，如果放置的位置已经被占用，就要循环右移，直到没有被占领的位置为止，然后将相应的行放在这个位置。

行置乱的向量如表6所示。

表6　行置乱向量

说明：按照上两步的规则，置乱后的行号排列为表6所示。在编程中，可以利用上面的向量对图像的行或列进行置换，本文是先对行置换，然后对列进行置换。

步骤3利用改进型Tent映射，两个初始值z0、q0和两个参数μ1、μ2，分别产生两个一维序列Z和Q。然后将Z和Q序列转化为M×N×8的二进制序列，同时需要随机产生一个1～M的整数n。然后利用Z序列对矩阵G2的前n行进行异或运算，剩余部分行利用Q序列进行异或操作，生成加密图像G3。

步骤4经过如上加密后，图像G3变为M×N×8的二进制二维矩阵，然后随机产生一个1～8的整数r1，根据它来决定使用表1所示的DNA编码规则中的哪种规则。根据DNA编码规则每两位二进制有1位脱氧核苷酸表示，从而将G3转化为一个M×N×4的DNA编码序列G4。

步骤5随机产生一个1～6的整数r2,从而决定使用如表2中的6种碱基对互补规则中的哪种规则。然后根据选择的规则来决定G4中的核苷酸替换的方法。替换后得到图像的矩阵G5。

步骤6随机生成一个1～8的整数r3，根据它来决定使用表1中哪种规则对G5进行转换，然后生成M×N×8的矩阵，也就是加密后的图像G6。

解密过程是加密过程的逆运算，在得到密文与正确密钥的情况下，通过解密过程就可以得到原始图像。

2.3密钥参数

本算法基于混沌占空置乱和DNA编码的图像加密算法，其采用的密钥参数如表7所示。主要由三个部分构成：混沌系统参数、图像分割参数和DNA编码参数。其中a0、ua是改进型Logistic映射的系统参数，a0取值范围为(-1.2,1.2)；ua取值范围为(2.35,3)时系统处于混沌态；z0、q0、wz、wq、k是改进型Tent映射的系统参数；z0、q0可以取(0,k)之间的任意值,其中k>1；wz、wq取值(1,2)时，改进型Tent映射处于混沌态；n是图像分割参数，它可以取(1,M)的整数，M表示图像的行数，r1、r2、r3是DNA编码时选择的编码规则的编号，可以参考表1和表2，其中r1取(1,8)的整数，r2(1,6)的整数，r3取(1,8)的整数,它们不同的取值会导致DNA编码结果截然不同。对于算法中参数的取值，分为三种情况分别如表7所示。对于混沌参数的取值要保证混沌系统处于混沌态，图像分割参数选取1～M之间的随机数，目的是增大密钥的空间，提高算法的安全性，DNA编码参数则要参照表1和表2的规则，解编码是编码的逆过程。

表7　密钥参数

3实验仿真及结果分析

3.1仿真实验

利用MATLAB软件，结合本文算法，对“lena.bmp”图像进行加密和解密的仿真实验，密钥选用：K=(0.70001, 2.55, 0.1, 0.1000001, 1.0001, 1.0002, 125, 3, 4, 2)，结果如图2、图3所示。

图2　加密过程图像

图3　解密过程图像

图2中(a)为原始图像，(b)为行置乱后图像，置换后图像的部分细节得到了隐藏，(c)为行列置乱后图像，图像明显比只进行行置换的图像(b)隐藏了更多的图像细节，(d)为置乱并Tent加密后图像,图像已经看不出任何的有效信息，(e)为置乱加密并DNA扩散后生成的最终加密图像，即密文，已经完全看不出任何图像的信息，说明加密效果良好。

图3中(a)为密文，(b)为DNA扩散恢复后的图像，(c)为Tent解密后的图像，图像的部分信息已经呈现出来，(d)为列置乱恢复后的图像，(e)为最终的解密图像，解密后图像几乎可以呈现出原始图像的全部信息。

通过比较得知，原始图像图2(a)与解密后图像图3(e)，像素点完全相同。仿真结果可以得出，本文提出的算法没有丢失图像的任何信息。

3.2统计特性分析

3.2.1直方图分析

直方图是图像每个像素点灰度值与其出现的次数之间的统计关系[14]。如果加密后的图像频率统计直方图可以呈现出均匀状态分布情况，那么就可以表明本文的加密算法能够很好地隐藏明文图像的统计特性，加密效果明显[12]。图4中(a)是原始图像的频率直方图，(c)是解密后图像的频率直方图，(a)和(c)的直方图基本相同，(b)是加密后的频率直方图，可以看出其分布均匀。结果表明，本算法具有较好的加解密效果。

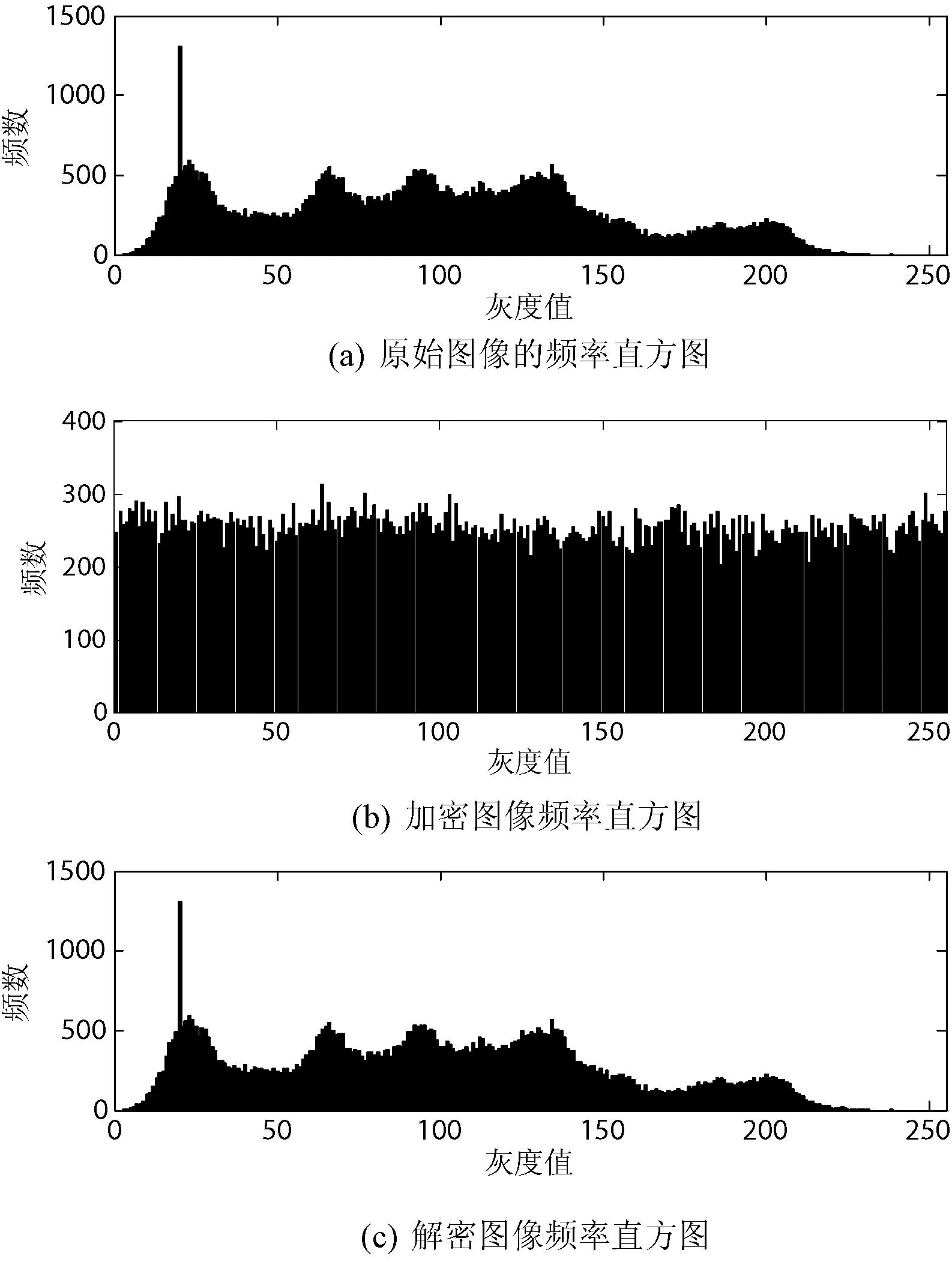
图4　加解密图像的频率直方图

3.2.2相关性分析

随机选取lena.bmp明、密文图像的1000对相邻像素点值进行相关性统计测试，其中包括水平、垂直、对角3个方向，结果如表8所示。从表8数据可以看出，明文图像中相邻像素存在着很大的相关性，而算法加密后图像相邻像素基本不存在相关性。水平方向选取明、密文中2560对相邻像素点灰度值，然后绘制其分布情况，如图5所示。由图5可以明显看出明文图像的相邻像素点灰度值成连续性特征，经过算法处理后，图像的连续性已经被完全置乱，图像相邻像素点的灰度值随机杂乱的分布，且布满整个二维空间。

表8　相邻像素相关系数

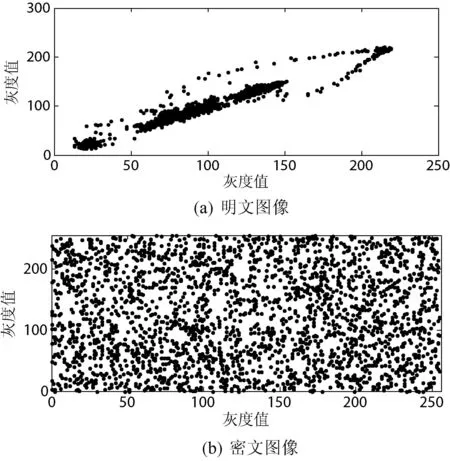
图5　图像相邻像素水平相关分布

3.2.3信息熵分析

图像信息熵计算式如下所示：

(4)

对于256级灰度图像其理想信息熵值为：H(x)=N=8。根据式(4)计算本算法得到的lena.bmp密文图像信息熵为7.9890，说明本算法对图像置乱充分，加密算法对抵抗熵攻击是安全的。

3.3密钥敏感测试

密钥敏感性指的是密钥很小的变化，就会产生两幅不同的加密图像[13]。解密密钥的很小变化就会导致无法成功解密图像。加密密钥设定为K=(0.70001, 2.55, 0.1, 0.1000001, 1.0001, 1.0002, 125, 3, 4, 2)，而解密密钥为K=(0.70002, 2.55, 0.1, 0.1000001, 1.0002, 1.0002, 125, 3, 4, 2)。

密钥微小的变化，结果如图6、图7所示。图6为错误解密图像及直方图，图7为正确解密图像及直方图。可见即使密钥微小的变化也会导致无法得到图像任何有效信息，说明此算法对初始值具有高度的敏感性，其具有对枚举搜索很好的抵抗力，说明算法的安全性很高。

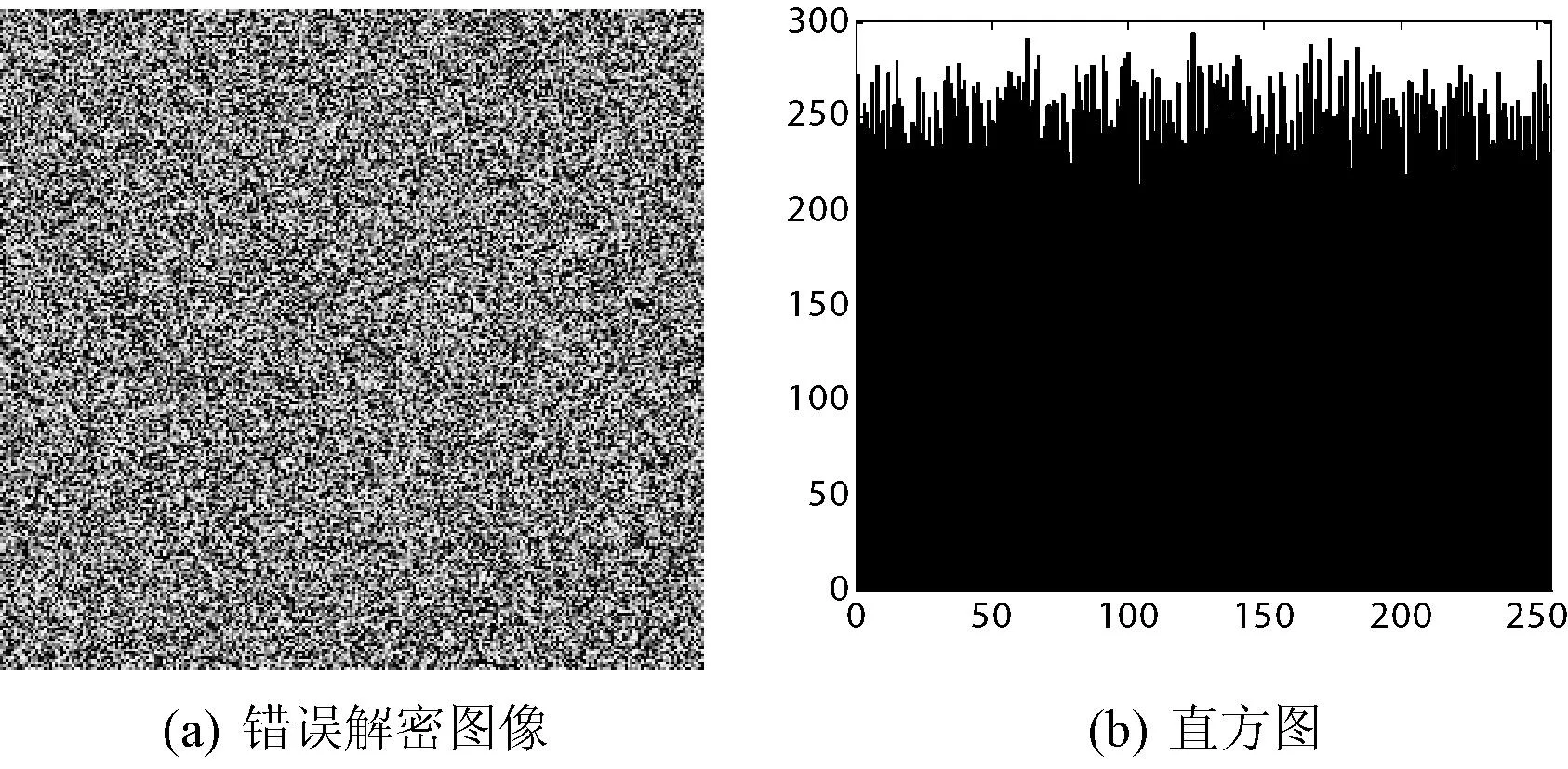
图6　错误解密图像及其直方图

图7　正确解密图像及其直方图

4算法性能分析

本算法采用混沌占空置乱和DNA编码方法进行加密，其复杂度主要体现在以下几个方面：

1) 该算法的密钥为K=(a0,ua,z0,q0,wz,wq,n,r1,r2,r3)，a0取值(-1.2,1.2)，z0、q0可以取值(0,k)之间的任何值,其中k>1，其密钥空间无穷大；ua取值(2.35,3)；wz、wq可以取(1,2)之间任意值，其密钥空间无穷大；n取(1,M)的整数，r1取(1,8)的整数，r2(1,6)的整数，r3取(1,8)的整数。由于密钥的变化，可以大大增加密钥空间，所以，对密钥K的穷举攻击无法破解加密。

2) 算法混沌占空置乱所采用的改进型Logistic映射相比原来的映射有着对初始值更好的敏感性。类随机性及不可预测性，不仅扩大了密钥的空间，而且也增加了密钥敏感性，较好地增强了图像加密效果。同时，占空法使用也极大地提高了算法的安全性。

3) 算法采用的改进型Tent映射相比原来映射有着更大的迭代空间，利用其产生的两个序列Z和Q。分别对图像矩阵的前n行像素点，和其余像素点进行异或运算生成加密图像，不仅扩大了密钥空间，而且如果改变n的值，就会得出不同的加密图像，从而极大地提高了整个算法的安全性。

4) 算法最后，利用DNA编码规则，对图像矩阵中像素点灰度值的每两位二进制位分别进行对应的互补替换，达到图像像素扩散的目的。进一步提高了加密效果，同时也极大地提高了算法的复杂性和安全性。

5结语

本文介绍了一种基于混沌占空置乱和DNA编码的图像加密算法。该算法以混沌理论为基础，将改进型Logistic混沌映射产生的混沌序列应用于图像置乱。然后使用改进型Tent映射产生两个混沌序列对置乱后的图像的前n行像素点和其余像素点分别进行异或运算。最后利用DNA编码规则，对图像矩阵中像素点灰度值的每两位二进制位分别进行对应的互补替换，达到图像扩散的目的，最终生成加密图像，即密文。

实验仿真及复杂度分析结果显示，该算法安全可靠，在信息存储、信息传输等实际应用中具有较大前景。

参考文献

[1] 丁玮,闫伟齐,齐东旭.基于Arnold变换的数字图像置乱技术[J].计算机辅助设计与图形学学报,2001,14(4):338-341.

[2] 万里红.三维Hilbert曲线在图像置乱中的应用[J].计算机工程,2011,37(2):227-231.

[3] 邵利平,覃征,衡星辰,等.基于矩阵变换的图像置乱你问题求解[J].电子学报,2008,36(7):1355-1363.

[4] 张燕,黄贤武,刘家胜.一种基于改进的混沌猫映射的图像加密算法[J].计算机工程,2007,33(10):166-168.

[5]WangQian,QiangZhang,ChangjunZhou.AmultilevelimageencryptionalgorithmbasedonchaosandDNAcoding[J].Bio-InspiredComputing,2009,10(9):1-5.

[6]JyotiChauhan,AnchalJain.SurveyOnEncryptionAlgorithmBasedOnChaosTheoryAndDNACryptography[J].InternationalJournalofAdvancedResearchinComputerandCommunicationEngineering,2014,3(8):7801-7803.

[7]HermassiH,BelaziA,RhoumaR,etal.SecurityanalysisofanimageencryptionalgorithmbasedonaDNAadditioncombiningwithchaoticmaps[J].MultimediaToolsandApplications,2013,72(3):2211-2224.

[8]MortezaSaberiKamarposhti,IbrahimAlBedawi,DzulkifliMohamad.ANewHybridMethodforImageEncryptionusingDNASequenceandChaoticLogisticMap[J].AustralianJournalofBasicandAppliedSciences,2012,6(3):371-380.

[9] 贺洁玲,王光义,王大朋.改进型Logistic映射及其在DES算法中的应用[J].杭州电子科技大学学报,2013,33(6):5-8.

[10] 翟依依,王光义.基于Tent混沌序列的数字图像加密方法[J].现代电子技术,2014,37(12):73-77.

[11] 陈宵.DNA遗传算法及应用研究[D].杭州:浙江大学,2010.

[12]PareekNK,VinodPatidar,SudKK.ImageEncryptionusingChaoticlogisticMap[J].ImageandVisionComputing,2006,2(6):1-9.

[13] 邓玥,王光义,袁方.一种新的Rossler混沌序列图像加密算法[J].杭州电子科技大学学报,2011,31(5):9-12.

[14] 董虎胜,陆萍,钟宝江.基于Henon映射与魔方变换的图像加密算法[J].计算机应用与软件,2014,31(5):291-294.

IMAGE ENCRYPTION ALGORITHM BASED ON CHAOTIC DUTY SCRAMBLINGANDDNAENCODING

Wang GuangyiRen GuoruiCui MingzhangCai Bozhen

(School of Electronics Information,Hangzhou Dianzi University,Hangzhou 310018,Zhejiang,China)

AbstractIn order to enhance the security of encrypted image, this paper proposes a new image encryption algorithm which is based on chaotic duty scrambling and DNA encoding. First the algorithm uses duty approach to randomly exchange the rows and columns of image matrix according to a pseudo-random sequence generated by the discrete chaotic map, compared with general chaotic scrambling, this greatly improves the operation speed; then it uses two pseudo-random sequences generated by another discrete chaotic map to conduct XOR operation on the pixels of front n rows of the image matrix and the remaining pixels respectively to generate the encrypted image; Finally, by employing DNA encoding rules, the algorithm correspondingly makes the complementary substitution for every two binary bits of the gray pixels values in image matrix separately to achieve the goal of image diffusion and finally generates the encrypted image. The simulation verification and analysis in regard to the statistical properties, key sensitivity and key space of the algorithm are carried out, the theoretical analysis on the complexity of the algorithm is made as well. Analyses results show that the algorithm has preferably high security.

KeywordsChaotic duty scramblingDNA encodingImage encryptionSafety analysis

收稿日期：2014-11-21。国家自然科学基金项目(61271064)。王光义，教授，主研领域：混沌保密通信，混沌电子电路，非线性电路分析，忆阻器建模与分析。任国瑞，硕士。崔明章，硕士。蔡博振，硕士。

中图分类号TP3

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.06.071