h-MMHC算法及其在主因素分析中的应用
2016-07-19李昌群程文娟
李昌群 杨 静 程文娟 安 宁
(合肥工业大学计算机与信息学院 安徽 合肥 230009)
h-MMHC算法及其在主因素分析中的应用
李昌群杨静程文娟安宁
(合肥工业大学计算机与信息学院安徽 合肥 230009)
摘要由于MMHC算法是针对所有的属性进行的网络结构图的构建,时间相对较长且结构图较为复杂。针对该情况,提出了启发式h-MMHC算法。它是MMHC算法的改进,从一个初始的属性集合出发,通过MMHC局部学习方法,借助启发策略,逐步添加新的属性,最终得到属性之间相关关系的贝叶斯网络结构。该研究以教学效果评估为实例,对于MMHC和h-MMHC算法做了比较。采用李克特量表法设计的调查问卷收集数据,使用两种算法对调查数据进行分析。相对于MMHC算法,由于减少了需要考虑的属性集规模,因此h-MMHC可更有效地应用于主因素分析中。
关键词h-MMHC算法贝叶斯网络主因素分析教学评估
0引言
特征提取问题是数据分析和挖掘的重要研究内容。恰当的算法可在众多的特征属性中,搜索到对于问题影响显著的特征集合,从而更有效地开展对于数据的深入分析。其中一个重要的问题就是主因素分析,也即在确定目标属性后,找出影响目标属性的主要因素。例如仝美红等人[1]利用主成分分析法以及熵值法来进行高校教师的绩效评价。主因素分析可以看作是特征提取的一种特殊形式,也即提取对于目标属性影响最大的一个或者若干个特征。
贝叶斯网络又称信度网络,自提出以来一直受到广泛的重视。在社会科学的研究中是一种常用的手段,其中包括教育研究领域,利用贝叶斯网络的模型来分析与教学质量相关的因素。例如,Choo-YeeTing等人[2]使用贝叶斯网络来构建一个基于计算机科学探索学习环境概念变化的计算模型;EvaMillán等人[3]使用贝叶斯网络来提高知识评估,使用通用贝叶斯学生模型的整合和评估,用于Aveiro大学的计算机测试中;EvaMillán等人[4]使用贝叶斯网络来设计和完善学生模型。依据该系统可以根据这些信息为学生们提供个性化的服务。同样的,国内学者也在利用数据分析的技术对影响高等教育质量的因素进行探索。马希荣等人[5]将数据挖掘中的关联规则分析技术应用到教学评价中,有效地挖掘教育研究中的数据;何万篷等人[6]将数学中的可拓方法与数据挖掘技术结合起来,挖掘影响教学质量的关键因素,以及教学质量与教师特征之间的关联规则。所有这些研究都可以归纳为对于某个目标的主因素分析。
对于属性的选择,研究者们在不断探索,正如魏浩等人[7]提出了基于相关性来进行属性选择。本文采用贝叶斯网络的方法从数据中获取属性之间的潜在关联。贝叶斯网络模型是一种概率网络,它可以用一个简洁明了的结构图来展示数据中蕴含的关联。结构图中的节点代表属性变量(随机变量),节点间的有向边代表属性之间的相互关联,用相关系数表达关联强度。利用贝叶斯网络模型作为教学效果的分析工具,可以有效地了解影响教学质量优劣的因素。特别是影响教学效果的主要因素。
MMHC算法是当前常用的构建贝叶斯网络的方法,但是对于主因素分析这样的问题,由于MMHC方法对于所有属性都是不加区别进行计算,存在计算量大,数据之间相互干扰问题。针对在主因素分析这样的特定应用,本文提出一种改进,即启发式MMHC算法,简称h-MMHC算法。该方法通过初始的部分属性集出发,逐步删除对于目标属性影响不大的属性,添加新的属性来迭代式逼近实际的贝叶斯网络。由于是逐步添加属性,而不是一次性对于所有属性进行计算,因此在主因素分析的应用中,h-MMHC算法具有计算量小,计算过程清晰的优点。通过对于一门课程教学效果的评估案例,探讨了h-MMHC算法构建贝叶斯网络的实际效果,以及在主因素分析中的应用。
1贝叶斯网络模型
一个贝叶斯网络是一个有向无环图,由代表属性的节点及连接这些节点的有向边构成。贝叶斯网络的学习过程实质上是在结构空间中寻找与样例数据集联合概率分布最一致的网络结构。通常采用基于评分和约束满足的学习方法进行结构的学习。
定义1[8]贝叶斯网络BN是一个二元组B=
一般地,令S是实例的集合,V是实例属性的集合,贝叶斯网络刻画了各属性之间的相关程度。确定贝叶斯网络结构主要是确定各属性之间的条件概率分布,由此可以得到关于各属性之间相互依赖程度的信息。本文中假定相关关系都是指线性相关。线性相关是一般相关关系的近似,在实际确定贝叶斯网络的结构时,经常考虑线性相关。并且,本文假定属性是相互独立的。
定义2[9]设V={X1,X2,…,Xn}是变量集合,若相关系数ρ(Xi,Xj)=0,则称Xi与Xj(线性)独立,记为Ind(Xi,Xj)。若Xi和Xj独立,则有p(Xi|Xj)=p(Xi),即变量Xj的任何变化对变量Xi的概率分布不产生影响。
在贝叶斯网络中,经常考虑一个节点关于其他一组节点的独立性。即下所述贝叶斯网络中的条件独立性。
定义3[10]贝叶斯网络中的条件独立性令Q(X)是一个节点X的所有父节点和子节点的集合,也就是说,Q(X)是X的马尔可夫覆盖,那么对于其他任何不在Q(X)中的节点Y,Y与X关于Q(X)是条件独立的,即ρ(X,Y|Q(X))=0,记作IndQ(X)(X,Y)。
在实际应用中,通常设置一个阈值δ,当相关系数ρ(X,Y|Q(X))<δ时,就认为它们是独立的,这个阈值称为关联阈值。
2启发式MMHC算法
从大量的数据中学习出一个网络,是机器学习领域的一个重要内容。对于一个样例,有多个属性去描述它。在现实世界中,实例的属性之间往往是存在一定关联的。对属性之间的关联性可以用不同的方法去描述。
MMHC算法又称为最大最小爬山算法,它基于约束的思想,结合了局部学习以及搜索评分技术的原则和有效方法。对于小样本的数据集,该算法也能够表现出很好的性能[11]。
利用MMHC算法从训练数据集中学习贝叶斯网络主要经过两个阶段:阶段一,找出各个节点的直接父节点。该阶段利用MMPC算法学习得到每个节点的父节点和子节点集合,学习过程中,利用条件独立性测试,如果变量X、Y关于变量集Z条件独立,即Ind(X,Y|Z)成立,则可以说明X和Y之间没有直接的联系,相反则说明存在直接的父子节点联系。在整个阶段一,利用该方法对各个节点做一次计算,最终得到所有变量的候选父子节点。阶段二,确定节点联系,即边的定向阶段。在该阶段中利用爬山算法去确定各个边,依次计算各个节点与候选父子节点的相关系数,从中选择出相关系数最大的节点对,添加边,即完成了所谓的定向。按照此方法不断的执行,最终定向出图中所有的边。
MMHC算法描述:
该算法主要分为约束阶段和搜索阶段。
输入:数据集D
//约束阶段
为每个变量X∈V计算其候选父节点和子节点集,计算PCx=MMPC(X,D)。
//搜索阶段
在受限的空间里通过执行贪婪的爬山搜索,包括添加边,删除边,逆置边等操作,找到具有最优评分的网络G, 只有当y∈PCx时才执行添加边Y→X操作。
输出:关联贝叶斯网络结构图G
MMHC可以被看做是SC(稀疏候选)算法[12,13]的一个特殊实例,也可以被归为使用两种方法的概念和技术的混合方式。对于SC算法,其要求用户估计参数K来进行约束限制,而MMHC算法有效地解决了SC算法中的不足,最突出的就是它无需用户估计参数K,从而使得该算法在计算量上大大减少。有关MMHC算法更多的细节可参看文献[11]。
MMHC算法假设贝叶斯网络是忠实的,即概率分布满足Markov条件。只有在极少数情况下,这个假设才可能不适合(细节参见文献[14])。
MMHC算法实际上是通过搜索-评分两个步骤确定出一个节点的父节点和子节点。从而形成数据之间概率关联关系的贝叶斯网络。如果相对于节点A,A的父节点Pa(A),节点B关于Pa(A)与A是条件独立的,则B与A之间没有边,也即B与A之间没有直接关联。在这样的前提下,关于属性集V=(v1,v2,…,vn)的联合分布概率:
P(v1,v2,…,vn)=∏P(vi|Pa(vi))
由此公式,可以容易计算出对于目标属性的主要影响因素,即主因素。
MMHC算法已经是目前比较流行的方法,并且写进了Matlab,成为标准算法之一。但是MMHC算法有一个缺点,即所用来确定贝叶斯网络结构的属性集合是所有属性,这就造成计算量大的问题。在主因素分析中不尽合理,因为主因素分析并不要求所有的属性之间的关联,而是只需要找出与目标属性具有最大关联的属性。本文结合主因素分析这种特定的应用场合,提出了一种从局部属性集合出发,逐步增加新属性的学习方法,进行网络结构的调整,最终得到主因素。用这样的方法可以提高计算效率。相对于原来的MMHC算法,本文提出的方法属于逐步逼近的贝叶斯网络结构学习。其基本思想是,在样例属性集合中,首先取出一部分属性,根据MMHC算法,建立有关这部分属性的贝叶斯网络结构,也就是建立这些属性的关联关系。然后将其中与目标属性关联度不大的属性屏蔽,增添新的属性,继续应用MMHC算法,构建新的贝叶斯网络。由于每次处理的属性数量较少,因此比起传统的MMHC算法,它的复杂度要低,并且容易揭示与目标属性最相关的影响因素。这种方法用于主因素分析中具有明显的优点。由于这种算法使用了对于属性学习的启发策略,因此称为启发式MMHC算法,记作h-MMHC算法。
定义4设S是贝叶斯网络学习任务L的实例集合,V是实例中属性的集合,d是某个特定的目标属性,与d的关联值超过某个阈值δ的属性称为影响d的主因素。
注意在此定义中,主因素可以不止一个。关联阈值δ根据问题的需要选取。
由于贝叶斯网络可以直接给出各属性之间的关联程度,因此贝叶斯学习和贝叶斯网络结构经常成为主因素分析算法采用的技术。本文提出的h-MMHC算法是一种改进的方法。
h-MMHC算法具体的流程如下:
(1) 令V为所有属性的集合;d为目标属性;关联阈值δ。
(2) 随机的选取部分属性集T⊂V,d∈T,利用MMHC算法构造关于T的贝叶斯网络B,即B=MMHC(T)。
(3) 对于所有z∈B,并且z∉Pa(d),若ρ(z,d)<δ,则删去z。
(4) 令删去的属性集为Z;添加属性集M,T=(T-Z)∪M,执行步骤2、步骤3。
(5) 直到所有的属性都完成,得到最终的结构图。
h-MMHC算法采用启发式的步骤,分阶段的添加属性,而且每次迭代计算时,只需要对含有M中的属性变量进行新的搜索和评分,实际运行表明,这种方法在很大程度上减少了计算量。这是h-MMHC算法区别于MMHC的独特之处。
该算法的正确性依赖于下面的一个定理。
定理1令S为属性的集合,d是目标属性,Z和M是两个属性子集合,对于任意属性X和Y,如果关于Z,X∉pa(d),那么关于Z∪M,同样有X∉pa(d)。
证明:根据MMHC算法,X∉pa(d),意味着IndZ(X,d),其中Z⊂pa(d),即X和d关于Z是条件独立的。这时如果增加新的属性子集M,则由MMHC的最大最小原则,只要有d的父节点子集Z使得IndZ(X,d),则X也不会添加到新结构中目标属性d的父节点。
定理1说明,当屏蔽一些属性,在增加一些属性重新计算关联性的时候,不会把原来非目标属性的父节点变成父节点。但是,对于已是父节点的属性,可能会由于新的属性加入而变成不是父节点,此时,会有新的父节点替代原来的父节点。因此h-MMHC算法在逐步添加属性将会逐步得到目标属性附近的正确结构。
定理2给定学习样例集S,对于任意初始的包含目标属性d的属性集合,h-MMHC算法都能正确收敛到d的附近的结构。
针对定理2,作两点说明。第一,h-MMHC的正确性依赖于学习样例集,不同的学习样例集可能给出不同的贝叶斯结构。第二,所谓目标属性附近的结构,是指距离目标属性最近的那些节点,至少包含所有的父节点(子节点不必考虑,因为不属于主因素问题的内容)。具体的界定需要根据问题确定,因为在实际中,存在一些节点,他们对于目标属性最终有较高的关联值,但却不是父节点。这是h-MMHC算法的一个缺陷。这一缺陷可以通过对于主因素再做主因素分析来弥补,也就是通过二次的主因素分析来得到这些属性,这样的属性可以称为次主因素。当然,这种情况是较少发生的,除非该属性对于某个主因素有较高的单向相关性,一般而言,这样的属性设计是较少碰到的。
关于每次需要添加的属性,既可以根据事先制定的添加策略自动添加,也可以根据专家先验知识和样例分布特征选择性添加,因此h-MMHC的属性添加具有灵活性,可以根据问题的需要而裁量考虑。
3应用案例—课程评估
近期我们把主因素分析用于教学效果的评估。该工作在《网络、群体与市场》课程中进行,这是面向本科大二学生,整个教学过程包括32个学时,为选修课程;一个年级总共180人,除了讲授以外还会留一些开放性的题目,以及相应的资源网站,便于学生们课后学习;整个教学分为四个阶段,在每个阶段通过问卷了解教学效果,基本方法就是贝叶斯网络的主因素分析方法,以确定影响教学效果的主要因素。并且根据分析的结果,剔除对于教学效果影响不大的因素,重新设计新的问卷,引入新的因素,在课程的下一阶段使用新的问卷进行了解,结合前次的分析结果,综合给出教学效果的评价。为了确保问卷题目的准确性,采用不记名式的作答;对收集回来的数据运用统计学的方法以及贝叶斯理论中的h-MMHC算法进行分析。
针对教学阶段的自然划分,采用分阶段式的设计问卷。这样每个阶段的题目数不用太多,一方面不会让学生们产生负担,从而可以更认真的作答;另一方面通过几个阶段的设计,题目的数量也达到了我们预期的数量,如此便不会影响考察的效果。具体的问卷设计如表1所示。

表1 各阶段的问卷设计
正如表1中所显示的,各期的问卷题目数量不变,为了与课程进度保持一致,问卷的题目内容是动态变化的,通过当前阶段的分析剔除不相关的题目,下一阶段在相应问卷位置加入新的题目。由于我们要考察的目标节点是6,也就是学生们对该课堂教学的总体评价。
在此案列中,整体的问卷题目是事先设定好的,分四阶段给学生进行问卷调查,问卷调查的题目有部分是重合的。根据上一阶段的分析结果来确定下一阶段的添加属性(问卷题目)。因此,在本案例中,属性添加参考了专家先验知识。事实上,也可以事先将全部属性制作成属性列表(问卷题目列表),根据某种策略进行属性的自动选取,例如事先规定的属性选取顺序或者是根据各阶段应该选取属性的数量。根据定理2,不同的属性添加策略对于主因素的筛选没有影响。
4实验结果以及分析
4.1数据集
本门课共180个学生选修,由于每次上课不是每个学生都会到场,而我们的问卷只是针对到场的学生进行考察。因此,一共32课时,收集回来的数据一共是1713条数据。问卷的设计中考虑到数据的离散化与连续的问题,采用李克特量表法进行问卷设计。李克特量表是一种心理反应量表,常在问卷中使用,而且是目前调查研究中使用最广泛的量表(http://baike.baidu.com/view/1574087.htm?fr=aladdin)。当受测者回答此类问卷的项目时,他们具体的指出自己对该项陈述的认同程度。由此收集回来的数据皆为离散化的数据,由于MMHC算法是一个专门用于离散数据的贝叶斯网络学习算法,因此,离散化过程是必须的。
香娭毑给人的印象是一个能干婆,可她见了喜姑,妹妹长妹妹短的叫得十分亲热,从不在她面前逞能的。没事的时候,喜姑也喜欢到香娭毑家里来串门。无论白天晚上,刮风下雨,只要喜姑一到,香娭毑就把宝刚爹支走,去去,到外面去,我们姊妹打讲,你到屋里凑什么热闹。
4.2各阶段结构图分析
对于调查问卷收集回来的数据,本文采用h-MMHC算法进行测试。此次的实验是在一台CPU是Inter(R) 2.94GHz,内存为4GB,操作系统为windows7的电脑上进行的。部分代码采用的是Causal-ExplorerMatlab_R14工具包。该研究中的各个阶段属性个数较少,故通过人为分析即可(例如,利用专家先验知识)。当属性个数较多时,可以在MMHC的构图阶段根据事先设定好的属性添加策略,逐步进行属性筛选,从而达到自动解析的目标。
如图1所示的是第一阶段收集回来的数据得到的网络结构图。对节点6(总体评价)有直接影响的节点分别是节点2(授课人讲解生动度)和节点4(学生对该堂课的兴趣度)。通过表2可以知道节点2和节点6之间的相关性达到0.513,节点4和节点6之间的相关性甚至达到了0.576。目标是寻找的对课堂总体效果(即节点6)有直接影响的节点,所以在第一阶段的后期,删去对节点6只存在间接影响的1、3、5节点。

图1第一阶段中
表2第一阶段中的相关系数

节点对相关系数(1,5)0.541(2,4)0.472(2,6)0.513(3,2)0.412(4,5)0.61(4,6)0.576(6,1)0.552
MMHC算法下的结构图根据结构图可以得到的结论为:授课者对于授课内容讲解得越生动学生们就越感兴趣,从而对于该堂课的总体评价也就会增加。另外,学生们对该堂内容的兴趣度指数也会影响他们对于该堂课的总体评价。
通过结构图的表示以及条件相关系数的计算可以看到:节点1(课堂内容是否充实,信息是否充分),节点3(授课人与大家的互动做的如何)以及节点5(课堂内容是否实用)对于课堂的整体效果作用不大。有研究指出教学内容、教学方法会对教学效果产生影响的[15],这些结论似乎与此有所相关,应该是本门课程的实际情况,与学生和教师的具体状态有关,作为一门课程的效果调研,毕竟是第一手资料。在该研究中出现的现象可以解释为:授课者所讲授的内容在学生们看来并没有很充分以及很实用。图2显示的是第二阶段问卷收集到的数据,表3是第二阶段中的相关系数。

图2第二阶段中
表3第二阶段中的相关系数

节点对相关系数(2,5)0.452(2,6)0.582(3,2)0.464(5,1)0.48(5,4)0.557(5,6)0.578(6,1)0.528
MMHC算法下的结构图在第一阶段中找到了与节点6关系紧密的节点,分别是节点2和节点4,因此在第二阶段替换掉题目1、3和5。从替换掉间接影响的节点后得到的第二阶段的图中可以看到,节点2还是对节点6有影响而节点4此时却并非是节点6的直接影响因素。变换的节点5此时却成为影响总体效果的次直接影响因素。通过表3可以发现节点2和节点6之间的相关性是0.582,节点5和节点6之间的相关性是0.578。为了考察验证结点4与节点6之间的关联性,在第三阶段的问卷中仍然保留节点4。所以在第三阶段只替换掉节点1和节点3。
在第二阶段,根据h-MMHC算法可以知道,新增加了1、3、5节点,新增加了三个节点后,通过条件相关性可以发现节点4和节点6之间的相关性为0。节点4在该阶段忽然与6没有联系,也许是该阶段中学生们对于老师们所教授的内容兴趣度不高,从而不存在直接影响。基于这样的考虑,在第三阶段中仍然保留节点4,以进行验证。
根据结构图可以得到的结论为:授课者对于授课内容讲解得越生动,那么学生们对于该堂课的总体评价也就会越高。同样的,当授课者善于激发学生思考,带动学生们的思考积极性,那么该堂课的总体评价也是会很好的。
此外,新增加的节点,分别是节点1(课程安排时间是否合理)、节点3(授课人课前准备)对于节点6 没有影响,说明学生们对于课程上课时间不是很满意,产生的原因与当时授课者将上课时间安排在周末可能是分不开的。基于上课的内容比较分散,学生们对于授课者课前的准备没有很认可,所以在该阶段表现出这样的结果。
图3显示的是第三阶段问卷收集到的数据,通过前两个阶段的分析,我们依次找到了对总体课堂效果有直接影响的节点,分别是第一阶段的节点2、4和第二阶段的节点2、5。在前两阶段中,节点2始终是节点6的父节点,而节点4和节点6的关系发生了变化。为了验证节点4和节点6之间的关系,我们还是保留第二阶段的题目4,只更换了题目1、3。这样便得到了第三阶段的问卷。从该图中可以看到节点2和节点5都对总体评价产生影响,而节点4却成为了节点6的子节点。通过表4可以看到,节点2和节点6之间的相关系数是0.593,节点5和节点6之间的是0.584。
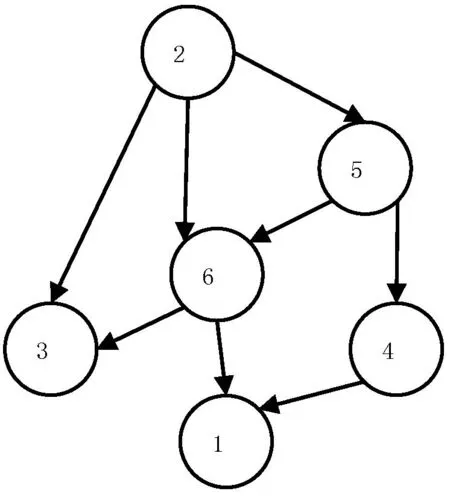
图3第三阶段中MMHC算法图
表4第三阶段中的相关系数

节点对相关系数(2,3)0.541(2,5)0.472(2,6)0.513(4,1)0.412(5,4)0.61(5,6)0.576(6,1)0.552(6,3)0.489(6,4)0.58
通过结构图可以得到的结论为:授课者对课堂内容讲解的越生动,那么学生们对于课堂效果的总体评价就越高。同样的,授课者如果善于激发学生们的思考,那么学生们同样会对该堂课的效果评价高。此外,当授课者善于激发学生思考的时候,学生们也就会对该堂课的内容越感兴趣。
被替换的节点1(课下是否愿意花时间去思考课堂上留下的问题)与节点3(该堂课是否达到期望)在该图中显示为受节点6的影响,说明在课堂效果评价好的情况下学生们会感兴趣,然后课下会愿意花时间去思考课堂上留下的问题,最终可以达到学生们的期望。但这两个节点不是影响6的直接因素。
图4是第四阶段收集到的数据得到的结构图。很明显可以看到该图与图3是没有变化的,那么这就说明在上一阶段得到的结论是成立的。也就是说尽管变动了1、3两个属性,节点2 和节点5对于课堂效果的总体评价仍是最有影响的属性。通过表5可以看到,节点2和节点6之间的相关性系数是0.58,而节点5和节点6的相关性系数是0.590。

图4第四阶段中MMHC算法图
表5第四阶段中的相关系数
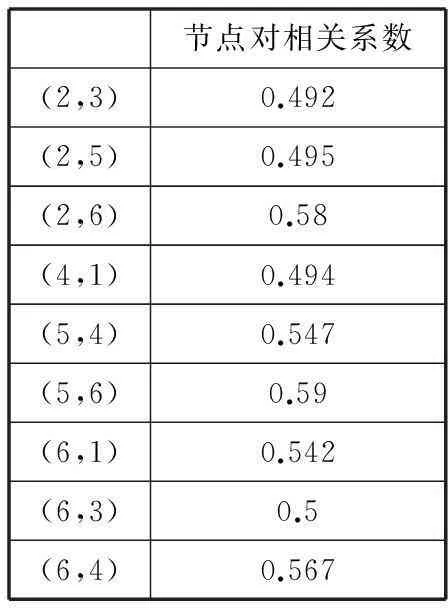
节点对相关系数(2,3)0.492(2,5)0.495(2,6)0.58(4,1)0.494(5,4)0.547(5,6)0.59(6,1)0.542(6,3)0.5(6,4)0.567
综合上述的结果可以说明:授课者对课堂内容讲解的生动度以及授课者善于激发学生们思考这两个因素节点通过使用h-MMHC算法被发现为是影响教学效果的主要因素。
第四阶段中新增的节点1(授课内容与实际的结合紧密度)与节点3(授课人的PPT制作效果)在该图中显示为节点6的子节点,说明这两个节点反而受节点6的影响。
基于上述对节点4的处理方式,也正验证了定理1的有效性。因此h-MMHC算法在逐步添加属性的过程中将会逐步得到目标属性附近的正确结构。
4.3MMHC的结构图
相比于h-MMHC的分阶段添加属性节点,MMHC则一次性将所有属性节点添加进来。在该研究中,一共有13个属性,对应的结构图中有13个节点。结构如图5所示,相关性系数见表6。
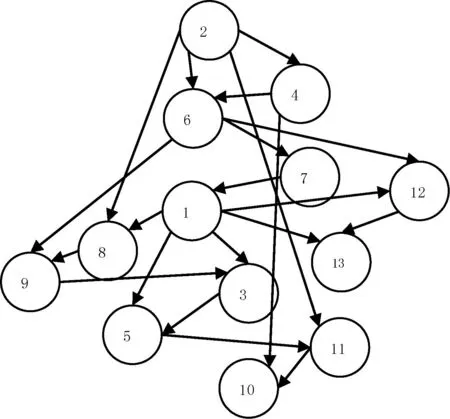
图5MMHC结构图
表6MMHC的相关性系数

(2,6)0.58(4,6)0.43(6,9)0.55(6,7)0.48(6,12)0.31
通过图5可以看到节点2和节点4对节点6是有影响的。该结论与h-MMHC的结论基本上是一致的。
限于篇幅的原因,在此只选取部分与节点6有关的节点对的相关系数。通过该表可以验证h-MMHC的正确性,即分阶段的添加属性节点进而获取主要影响因素是合理的。
4.4h-MMHC与MMHC的对比
从表7中可以看出h-MMHC算法和MMHC算法的区别之处。图中的运行时间是50次运行后计算得出的平均时间。很显然使用h-MMHC算法的整体运行时间少于MMHC算法的时间,时间相对来说提升了80%。就结构图的复杂度来说,h-MMHC算法相对于MMHC结构图较为清晰。

表7 h-MMHC和MMHC的对比
5结语
本文通过对于MMHC方法的改进,提出了h-MMHC方法,在主因素分析过程中可以更加有效地确定影响目标属性的主要因素。这种启发的策略来源于实际问题,并且通过逐步添加属性来实现对于主因素的确定和比较。在本文的应用案例中,将问卷中的13个属性,分阶段添加进来,每个阶段都会删去影响不占优的属性,在下一阶段添加新的属性,由于上一阶段已经删去了与目标属性没有直接关系的属性。通过实验可以验证h-MMHC算法相对MMHC算法来说具有运行时间少以及结构图简单的优点。
在社会科学研究中,这种启发式的主因素分析方法提供了更加灵活的数据处理方式。由于启发策略可以根据具体问题来合理选取,因此在很多场合中这种方法看起来会更加有效。同时也避免了MMHC方法对于所有属性一次性处理带来的计算资源上的耗费。本文通过教学评估的一个实际例子,比较了MMHC和h-MMHC两种方法的计算效果,其得到的结论是一致的,但是在耗费计算资源方面有明显差别,h-MMHC方法能够更快地完成计算。当然也需要指出的是,在这个案例中,有些结论和相关关系是与该案例的特殊情况有关,并不具有一般性。我们关心的是h-MMHC算法在这个案例中的应用。
参考文献
[1] 仝美红,段富.基于主成分分析和熵值法的高校教师绩效评价[J].计算机应用与软件,2014,31(1):62-64,169.
[2]TingChooyee,YokchengSam,CheeonnWong.ModelofconceptualchangeforINQPRO:ABayesianNetworkapproach[C].Computers&Education,2013,65:77-91.
[3]MillánE,DescalçoL,CastilloG,etal.UsingBayesiannetworkstoimproveknowledgeassessment[J].Computers&Education,2013,60(1):436-447.
[4]MillánE,LobodaT,Pérez-de-la-CruzJL.Bayesiannetworksforstudentmodelengineering[J].Computers&Education,2010,55(4):1663-1683.
[5] 马希荣,孙华志.数据挖掘技术在教学评价中的应用[J].计算机工程与应用,2003,39(19):51-54.
[6] 方耀楣,何万篷.可拓数据挖掘在高校教学质量评价中的应用[J].数学的实践与认识,2009(4):82-87.
[7] 魏浩,丁要军.一种基于相关的属性选择改进算法[J].计算机应用与软件,2014,31(8):280,284.
[8] 何德琳,程勇,赵瑞莲.基于MMHC算法的贝叶斯网络结构学习算法研究[J].北京工商大学学报:自然科学版,2008,26(3):43-48.
[9] 杨静,曹家俭.连续贝叶斯网络模型在断面调查数据的应用[J].计算机工程与应用,2014,50(19):192-198.
[10]RussellStuart,PeterNorvig.人工智能—一种现代方法[M].清华大学出版社,2002.
[11]TsamardinosI,BrownLE,AliferisCF.Themax-minhill-climbingBayesiannetworkstructurelearningalgorithm[J].Machinelearning,2006,65(1):31-78.
[12]FriedmanN,LinialM,NachmanI,etal.UsingBayesiannetworkstoanalyzeexpressiondata[J].Journalofcomputationalbiology,2000,7(3-4):601-620.
[13]FriedmanN,NachmanI,PeérD.LearningBayesiannetworkstructurefrommassivedatasets:the≪sparsecandidate≪algorithm[C]//ProceedingsoftheFifteenthconferenceonUncertaintyinartificialintelligence.MorganKaufmannPublishersInc,1999:206-215.
[14]MeekC.StrongcompletenessandfaithfulnessinBayesiannetworks[C]//ProceedingsoftheEleventhconferenceonUncertaintyinartificialintelligence.MorganKaufmannPublishersInc,1995:411-418.
[15] 徐秋云.影响课堂教学效果的主要因素分析[J].科技信息(学术研究),2007(30):197.
H-MMHC ALGORITHM AND ITS APPLICATION IN PRINCIPAL FACTORS ANALYSIS
Li ChangqunYang JingCheng WenjuanAn Ning
(School of Computer and Information,Hefei University of Technology,Hefei 230009, Anhui,China)
AbstractSince MMHC algorithm is a construction of network structure diagram for all properties, its operation time is relatively long and its chart is somewhat complicated. In view of this, we propose the heuristic h-MMHC algorithm, which is an improvement of MMHC. Starting from an initial attribute set, the h-MMHC algorithm utilises MMHC local learning method and heuristic principle to add new attributes incrementally, and eventually obtains the Bayesian network structure of correlation relationship among attributes. Using teaching effect evaluation as a concrete example, in the paper we compare MMHC and h-MMHC algorithms: using the questionnaire designed by Likert scale method to collect data and employing these two algorithms to analyse the surveyed data. Relative to MMHC algorithm, due to the decrease in the size of attribute set to be considered, h-MMHC can be better applied to principal factors analyses.
Keywordsh-MMHC algorithmBayesian networkPrincipal factor analysisTeaching evaluation
收稿日期:2015-01-08。国家自然科学基金项目(61305064,5127 4078);安徽省重大委托教研项目(2012jyzd15w);大学计算机课程改革项目(教高司函,<2012>188号)。李昌群,硕士生,主研领域:贝叶斯理论应用。杨静,副教授。程文娟,副教授。安宁,教授。
中图分类号TP3-05
文献标识码A
DOI:10.3969/j.issn.1000-386x.2016.06.058
