An interactive approach for functional prototype recovery from a single RGBD image

Yuliang Rong，Youyi Zheng，Tianjia Shao（），Yin Yang，and Kun Zhou○cThe Author（s）06.This article is published with open access at Springerlink.com



Research Article

An interactive approach for functional prototype recovery from a single RGBD image

Yuliang Rong1，Youyi Zheng2，Tianjia Shao1（），Yin Yang3，and Kun Zhou1
○cThe Author（s）2016.This article is published with open access at Springerlink.com

AbstractInferring the functionality of an object from a single RGBD image is difficult for two reasons: lack of semantic information about the object，and missing data due to occlusion.In this paper，we present an interactive framework to recover a 3D functional prototype from a single RGBD image. Instead of precisely reconstructing the object geometry for the prototype，we mainly focus on recovering the object's functionality along with its geometry. Our system allows users to scribble on the image to create initial rough proxies for the parts.After user annotation of high-level relations between parts，our system automatically jointly optimizes detailed joint parameters（axis and position）and part geometry parameters（size，orientation，and position）.Such prototype recovery enables a better understanding of the underlying image geometry and allows for further physically plausible manipulation.We demonstrate our framework on various indoor objects with simple or hybrid functions.

Keywordsfunctionality；cuboid proxy；prototype；part relations；shape analysis

1　Introduction

That form ever follows function.This is the

law.

Louis Sulliva n

1StateKeyLabofCAD&CG，ZhejiangUniversity，Hangzhou 310058，China.E-mail:Y.Rong，rongyl@ zju.edu.cn；T.Shao，tianjiashao@cad.zju.edu.cn（）；K. Zhou，kunzhou@cad.zju.edu.cn.

2ShanghaiTech University，Shanghai 200031，China.E-mail:zhengyy@shanghaitech.edu.cn.

3The University of New Mexico，Albuquerque，NM 87131，USA.E-mail:yangy@unm.edu.

Manuscript received:2015-12-01；accepted:2015-12-09 WiththepopularizationofcommercialRGBD cameras such as Microsoft's Kinect，people can easily acquire 3D geometry information with an RGB image.However，due to occlusion and noise，recoveringmeaningful3Dcontentsfromsingle RGBD images remains one of the most challenging problems in computer vision and computer graphics. Over the past years，much research effort has been devoted to recovering high-quality 3D information from RGBD images［1，2］.Most of these approaches，starting either from a single image or multiple images，are dedicated to faithfully recovering the 3D geometry of image objects，while their semantic relations，underlying physical settings，or even functionality are overlooked.More recently，research has explored use of high-level structural information to facilitate 3D reconstruction［3-5］.For example，Shao et al.［3］leverage physical stability to suggest possible interactions between image objects and obtainaphysicallyplausiblereconstructionof objects in RGBD images.Such high-level semantic information plays an important role in constraining the underlying geometric structure.

Fig.1　Objects in man-made environments are often designed for single or multiple intended functionalities.

Functionality is the center of object design and understanding.Objects in man-made environments are often designed for single or multiple intended functionalities（see Fig.1）.That form ever followsfunction is the law of physical manufacturing［6］. In this paper，we develop an interactive system to recover functional prototypes from a single RGBD image.Our goal is to allow a novice user to be able to quickly lift image objects into 3D using 3D prototypes，using just a few high-level annotations of joint types and geometric/functional relations；the user can meanwhile explicitly explore and manipulate an object's function.We focus on prototypes with simple proxies（e.g.，cuboids）representing their parts as a means to alleviate the difficulties of precise 3D reconstruction which is a harder problem.By taking physical functionality into consideration，we may gain a much more faithful interpretation of the underlying objects. The functional properties can then be used for applications like in-context design and manipulation.

Itisachallengingproblemtoinferobject function just from user annotated joint types and geometric/functional relations.Our system should automatically optimize the detailed joint parameters （axis and position）in order to make the parts move correctly，whereas this task is typically done in CAD software by the user repeatedly adjusting parameters.Furthermore，initial proxies from usersegmented depths are often rough with incorrect orientation and position，and may be incomplete because of occlusion.Hence initial proxies often fail to satisfy the functional relations such as A covers B. Therefore our system should also optimize the proxy parameters（size，orientation，and position），in order to make parts satisfy functional relations.

Our method starts with a single RGBD image. The user segments the image object into parts by scribbling on the image using simple strokes or polygons.Then each segmented part is assembled using a 3D proxy.We use simple cuboids in this paper［7］.Given the initial proxies，our system then allows the user to annotate the joint types and functional/geometric relations between parts.In a key stage，our algorithm simultaneously optimizes the detailed joint parameters（axis and position）and the proxy parameters（size，orientation，and position）.Finally，a functional prototype is produced with moving parts satisfying the user annotated relations.

We have tested our system on a variety of manmade hybrid functional objects taken from various sources.Our results show that even using only a few user annotations，the proposed algorithm is capable of faithfully inferring geometry along with appropriate functional relations for the object parts.In summary，this paper makes the following contributions:

·Identifyingandcharacterizingtheproblem of integrating functionality into image-based reconstruction；

·Simultaneous optimization of detailed joint andgeometryparametersfromuser's high-levelannotationsofjointtypesand functional/geometric relations；

·An interactive tool for functional annotation which has been tested on a variety of indoor scene images and physical designs.

2　Related work

Proxy-based analysis.A significant amount of work has leveraged proxies to understand objects or scenes.Li et al.［8］and Lafarge et al.［9］consider globalrelationshipsasconstraintstooptimize initial RANSAC-based proxies to produce structured outputs；similarly，Arikan et al.［10］use prior relations plus user annotations to create abstracted geometry.For scene analysis，many approaches encode input scenes as collections of planes，boxes，cylinders，etc.，and study their spatial layout［11-16］.Recently，proxies have frequently been used in functionality analysis of a design.Umetani et al.［17］use physical stability and torque limits for guided furniture design in a modeling and synthesis setting.Shao et al.［18］create 3D proxy models from a set of concept sketches that depict a product from different viewpoints，with different configurations of moving parts.Our work is inspired by Koo et al.［7］，who annotate cuboids with highlevel functional relationships to fabricate physical work-alike prototypes.Unlike their algorithm，our framework does not require explicitly creating joint positions，as we consider a larger search space to automatically infer the joint and part parameters. To our knowledge，we are the first to focus on proxy-based functionality recovery from a single RGBD image，in particular recovering how the object works by jointly optimizing both part geometry and functional relationships based on user annotations.

Constraint-basedmodeling.Ourworkis related to constraint-based modeling research in the graphics and CAD communities.Similar work to ours involves the automatic determination of relevant geometric relationships between parts for high-level editing and synthesis of 3D models［5，19-21］.Previous mechanical engineering research has used declarative methods for specifying relevant geometric constraints for a mechanical design［22，23］.Some professional CAD software like AutoCAD and SolidWorks contains constraint-based modeling modules，butusersarerequiredtomanually adjustthelow-levelpart/jointparametersto specify relationships.In contrast，our system can automatically interpret user annotated high-level functionality to give specific geometric constraints.

3D modeling from a single RGBD image. Much effort has been devoted to obtaining highquality geometry information from a single RGBD image［1，24］.To recover structural information，Shen et al.［4］extract suitable model parts from a database，and compose them to form highquality models from a single RGBD image.Shao et al.［3］use physical stability to recover unseen structures from a single RGBD image using cuboids. However，their techniques focus on creating static 3D geometry and structure，whereas our goal is to produce models with correctly moving parts.

3　Overview

As illustrated in Fig.2，given a single RGBD image，we first let the user scribble strokes over an image object to separate out its functional parts.These parts，being either a semantic component or an added object，are used during function recovery. To segment the parts，we use a depth-augmented version of the GrabCut segmentation method［25］，as Ref.［3］does.Optionally，if the color and depth are too similar，making it difficult to separate the parts with GrabCut，the user may use a polygon tool as in PhotoShop to perform segmentation （see the accompanying video in the Electronic Supplementary Material（ESM））.We assemble a set of cuboid proxies，one fitted to each individual part. The user then annotates high-level relations between these cuboids.The relations are of three kinds: joint type relations（e.g.，hinge，sliding），functional relations（e.g.，covers，fits inside，supports，flush，connects with）［7］，and geometric relations（e.g.，equal size，symmetry）.

Given the user annotated relations，in a key step，our method recovers each cuboid's orientation，position，and size along with the joint parameters using a combined optimization approach.We use a combined optimization strategy because the cuboid parametersarealwayscoupledwiththejoint parameters:given a set of joints，the cuboid geometry must be adjusted to satisfy the functional constraints.

Optimization is done using a two-stage sampling strategy.In the first stage，our algorithm samples possible cuboid edges as joint candidates［18］for the specified joint type.Given one set of possible joint candidates，the cuboid orientation is aligned and the cuboid position is refined，by adjusting the corresponding joint edges.We assume that the joint must be snapped to the nearest cuboid face and be parallel to the nearest cuboid edge（as in Ref.［7］）.

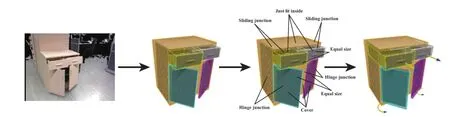
Fig.2　Algorithmic pipeline.Given the input RGBD image（left），our system generates initial proxy cuboids（mid-left）from parts segmented by the user with strokes or polygon tools.The user then annotates a set of high-level relations between the proxies including joint types and geometric/functional relations（mid-right）.Finally our system simultaneously optimizes joint parameters（axis and position）and part parameters（orientation，position，and size）to obtain a functional prototype with parts moving as the user expects（right）.

Having found one set of adjusted joints with cuboidorientationsandpositions，ourmethod further samples a set of possible candidate restconfigurations for the cuboids.A rest configuration isastatewheretheobjectisinaclosed state［7］.Because the cuboid size has not yet been definitively determined，the system does not know which state is the closed state.Thus we sample possible candidates for the rest configurations，as shown in Fig.6.For each possible rest configuration，we optimize the cuboid size parameters according to the user annotated functional/geometric relations as in Ref.［7］.Finally，the optimized cuboids which best match the initial point cloud are selected，and the best prototype with best joint and cuboid parameters is produced.We next describe the algorithm in detail.

4　Algorithm

Our method takes as input an RGBD image of a functional object.By functional we mean objects having particular moving parts，such as a door which opens by rotating，a sliding drawer，etc.Such objects are very commonly seen in our daily life，for instance，rolling chairs，folding tables，printers，seesaws，etc. Initial cuboid generation.Given the input RGBD image，our first task is to anchor the object's functional parts.Automatically identifying image objects and object parts in RGBD images has been explored in recent works，but without prior knowledge，such methods do not yet work well enough for our purposes.We resort to an interactive solution.As in Ref.［3］，we let the user scribble on the image object to specify object parts.In particular，we allow the user to draw free strokes over parts to indicate a segment（part）. We apply a depth-augmented GrabCut algorithm［3］to the underlying point cloud along with its pixel and adjacency information.Optionally，if the color and depth are too similar，making it difficult to separate the parts with GrabCut，the user may use a polygon tool as in PhotoShop to perform segmentation.We then run the efficient RANSAC

algorithm［26］on the seegmented points to generate candidate planes.The largest plane is selected as the primary plane，and the second largest plane is made orthogonal to the primary one.We extract initial cuboids determined by these orthogonal directions （the third direction is the cross product of the two plane normals）.Figure 3 illustrates the process of generating the initial cuboids.Note that the generated cuboid may have erroneous orientation，position，and size.In subsequent steps，our goal is to simultaneously optimize these parameters along with the joint parameters so that the extracted cuboids form a prototype whose functionality closely follows the image object.

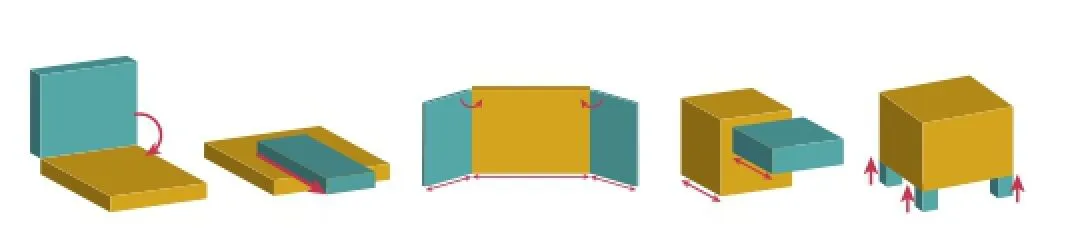
Fig.4　User annotated joint types and some typical functional relations.From left to right:hinge joint，sliding joint，exactly covers，just fits，and supports.

Fig.3　Initial proxy generation.The user is allowed to scribble strokes on the image（left）；based on the scribbles，depth-augmented GrabCut is applied to segment the input object into different parts （middle）.Initial cuboids are then fitted to the corresponding points （right）.

Relation annotation.Let the set of initial cuboids be（B1，...，BN）.An important first step is for the user to annotate the high-level relations between the cuboids.To this end，we define three categories of relations.Category I comprises joint relations（e.g.，A has a hinge relation w.r.t.B）. Category II comprises functional relations（e.g.，A covers B），while Category III comprises geometric relations（e.g.，symmetry，equal size）.In each case，the user selects a pair of cuboids and then indicates the relationship.

To further classify the relations，we define two main types of joint relations:hinges and sliding joints.For functional relations，following Ref.［7］，we define the following function types:A covers B，A fits inside B，A supports B，A is flush with B，and A is connected to B.The main geometric relations aresymmetryandequalsize.Theserelations impose different geometric constraints during the following optimization stage.Some relations might be dependent on each other；for example，if both A and C cover B，A is geometrically constrained w.r.t. B and C.Figure 4 shows the joint types and sometypical types of functional relations.Note that unlike Ref.［7］，we do not need to explicitly specify joint positions and axes as well as cuboid orientations and positions.Instead，we optimize these parameters in a combined manner.

Combinedoptimizationofcuboidsand joints.We now detail our cuboid optimization algorithm.Our goal is to simultaneously optimize the cuboids'orientations and shape parameters（i.e.，positions and sizes），as well as the detailed joint parameters，in accordance with the user annotated relations.The optimized cuboid configuration should deviate little from the input point cloud and move as the user expects.Given the input point cloud I and initial cuboids B=（B1，...，BN），along with the user annotated joint types J=（J1，...，JM），functional relations F=（F1，...，FP），and geometric relations G=（G1，...，GQ），we want to obtain the best joint parameters Θ ∗=（Θ∗1，...，Θ∗M）for the joint types J along with the best cuboids B∗=（B∗1，...，B∗N），satisfying the functional relations F and geometric relations G.We do so using the formulation:

Here E（B，Θ ，I）measures the deviation of the optimized cuboid configuration from the input point cloud，defined as

wherePkdist（Bj-pkj）measures the deviation of cuboid Bjfrom its associated points pkj.

The challenge is how to enforce the annotated relations as geometric constraints while ensuring the cuboids respect the input point cloud.Since the annotated relations are high-level specifications，this leads to a large optimization search space due to the potential ambiguities arising from the rather general annotations.Another challenge is that the cuboid parameters are highly coupled with the joint parameters.That is，given a set of joints，the cuboid geometry should change accordingly to satisfy the functional constraints.Thus we cannot optimize the parameters locally and separately，but must instead do so in a global manner.To solve the above challenges，we use a multi-stage optimization paradigm which first populates the solution space with a two-step sampling algorithm，and then jointly optimize the cuboid parameters and joint parameters.

In the first stage，we sample possible joint parameters，i.e.，axial position and orientation.Let us denote the set of joint types as（J1，...，JM），and the parameters we wish to estimate as（Θ1，...，ΘM）. We start by building a joint configuration graph.For each cuboid we create a graph node and for each joint type Ji，we create multiple graph connections，with each connection associated with a candidate parameter Θlifor Ji.If A forms a hinge relation with B，each cuboid edge of A can be a candidate hinge axis.We choose only those cuboid edges which are close to B.More specially，we only choose the edges parallel to the face if there is also a cover relation，and only choose the edges perpendicular to the face if there is a fit inside or support relation.This leads to a configuration graph where any traversal path of the graph represents a possible configuration of joints.Figure 5 shows such a graph.Algorithm 1 gives the pseudo-code for building the graph.

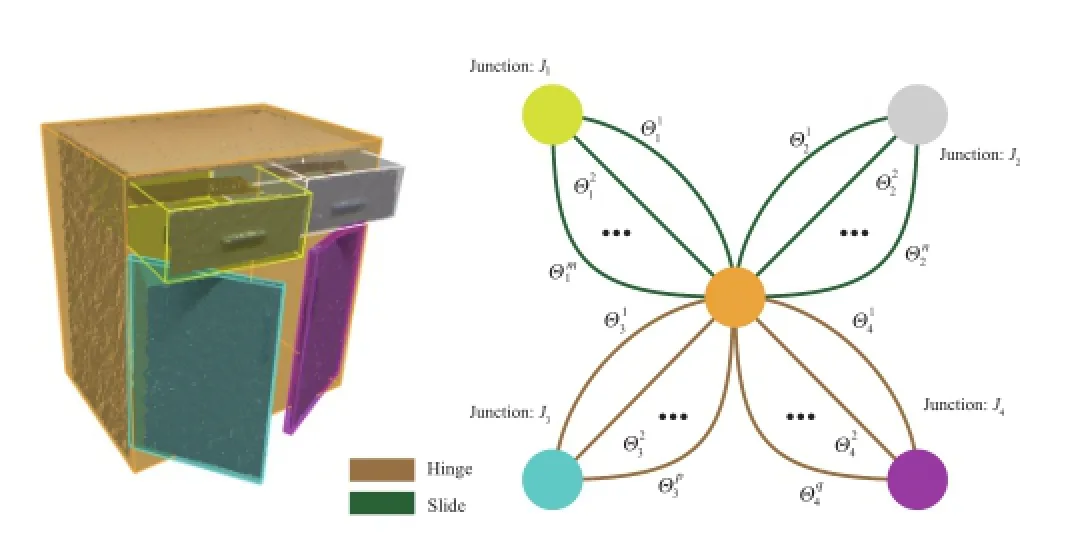
Fig.5　Junction　configuration　graph.Each　cuboid　shown corresponds to a node with the same color.Each annotated joint type corresponds to multiple connections between nodes.One connection is associated with one candidate joint parameter.

Given the joint configuration graph，for each jointconfigurationweoptimizeeachcuboid's orientation，position，and size based on annotated functional/geometricrelations.Thecuboid's orientation and position are firstly adjusted based on the current candidate joint configuration，by adjusting the corresponding joint edges.We assume that the joint must be snapped to the nearest cuboid face and be parallel to the nearest cuboid edge（following Ref.［7］）.Then we optimize the cuboid's size to satisfy the functional/geometric relations given by the current joint configuration. Note that the functional relations typically indicate the geometry of the cuboids in a closed configuration （i.e.，a rest configuration［7］.For instance，if A covers B，this typically means that one face of A is rotated about the hinge joint to be in closeagreement with a face of B（Fig.6）.Since we do not know which face covers B，we enumerate the possible cuboid faces to sample a set of rest configurations （see Fig.6）and for each rest configuration we optimize the cuboid parameters.Specifically，given a rest configuration of cuboids，we employ the optimization strategy in Ref.［7］to optimize the cuboid parameters（B∗1，...，B∗N）.We then compute the optimization cost from Eq.（2）.Finally，the configuration which best matches the point cloud is selected as the chosen configuration and the optimized cuboids are then computed.The overall algorithm is detailed in Algorithm 2.

Algorithm 1:　Build the junction configuration graph

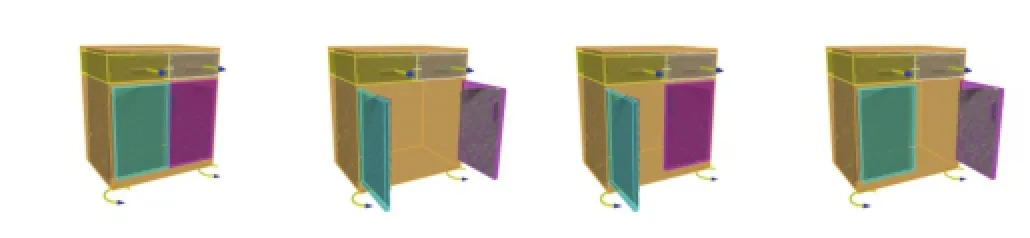
Fig.6　Possible rest poses for the hinge joints.　As we do not know which face of the cabinet door covers the cabinet，we rotate the hinge joints to sample a set of rest configurations to suggest possible covering faces.

5　Results

We show use of our system to recover functionality prototypes for 6 different objects（see Fig.7）.The first 4 examples（cabinet，drawer，firebox，and chair）are real RGBD images captured with Microsoft Kinect，while the last 2 examples（toolbox and dining table）are synthetic depth data generated from existing 3D designs.See the accompanying video in the ESM for how the various parts move and fit together.Creating a single functional prototype takes 30 to 300s for these examples.The time for user interaction（segmenting points with strokes and specifying part relationships，plus the waiting time for plane detection for initial cuboid generation）ranges from 27 to 108s，while the optimization time varies greatly，from 1 to 241s，depending on the size of the sampling space for joint parameters and rest poses.Experimental statistics（including the numbers of annotated hinge joints，sliding joints，functional relations，and geometric relations）are listed in Table 1.

Algorithm 2:Optimize cuboids and junctions

Fig.7　Experimental results.From left to right:the input RGBD image，initial cuboids，optimized cuboids and joints，and how parts move and fit after the optimization（3 configurations）.

As shown in Fig.2，although the geometry of our prototypes may appear simple，the relationships betweenthemovingpartsareoftencomplex. Manuallyadjustingthegeometryandrelation parameters would be very time and labor consuming. Our system automatically infers the joint parameters （position and axis）and the geometry parameters （size，position，and orientation）by optimizing them simultaneously under the user annotated high-level constraints.Satisfactory part parameters and joint parameters were obtained in all our experiments.For example，in Fig.7（1），our algorithm automatically placesthehingejointsonthecorrectedges of the cabinet doors，adjusts their orientations appropriately by aligning the hinge joints to the nearest cabinet face，and makes them parallel to the nearest cabinet edges.The sizes of the doors are also optimized to be of equal size and cover thecabinet.The drawers in Figs.7（1）and 7（2）have the desired orientations with their sliding joints aligned with the cabinet，and have sizes which properly fit inside the cabinet and are equal.In Fig.7（3），the lid and the front door are both optimized to just cover the firebox.In the chair example（Fig.7（4）），due to occlusion，the initial cuboids for the leg and the armrest have smaller sizes than they should，but our algorithm successfully extends the leg to support the seat，and extends the armrests to connect with the back.Similarly，the occluded leg in Fig.7（5）is extended to support the box and has the same size as the other legs.In Fig.7（6），the orientation and size of the two doors are optimized to support the table top，and the orientation of the top is optimized to be horizontal.

User study.To further evaluate whether our approach can recover correct functional prototypes，we showed our system to 20 students.5 were computer science undergraduates；4 students were master candidates in industrial design.The others were 8 master candidates and 3 Ph.D.candidates in computer science.We showed them the captured RGBD images and asked them to imagine how the objects work.These students then used our system to add annotations to the pre-generated initial cuboids based on their imagination.All students reported that our system successfully recovered functional prototypes in which the parts moved as they expected.Furthermore，the optimized part geometry also met their expectations.One exception was that 6 students said they imagined the hinge joint on the cabinet door in Fig.7（1）to be exactly at the edge of the cabinet，while our optimization did not consider it to be the best location.

Comparison with real objects and 3D design models.We also checked the recovered prototypes against the captured real objects and 3D design models.As illustrated in the top 2 rows in Fig.8，the generated prototypes have similar functionality to the real objects，and have parts which after movement give almost the same configurations as the real ones.Furthermore，the optimized simple cuboids approximate the real geometry well，with almost the same size，orientation，and position.We also compared our recovered prototypes with 3D design models whose joints were added and adjusted manually in Autodesk 3DS Max（bottom row in Fig.8）.We can see the prototypes recovered from the user's high-level annotations have very similar functionality to the manually designed models.

Fig.8　Top two rows:comparison with input data；bottom row:comparison with the 3D design model.Our system faithfully recovers the functionality the user expects.

6　Conclusions

In this work，we have presented a novel approach to recovering a functional prototype from a user's highlevel annotations of relationships.After indicating joint types and other functional/geometric relations，the joint parameters and part geometry parameters are simultaneously optimized.This interface allowsusers to focus on the functionality of the target object rather than working with low-level geometry and joint parameters.The results demonstrate that our system can generate functional models from a small number of user annotations.In the user study，the recovered prototypes worked correctly，as users expected.The comparison between the real objects and 3D design models further demonstrates the feasibility of our system.

Limitations and future work.The main limitationofourapproachisthatweuse cuboids as proxies to approximate part geometry. While compositions of cuboids are sufficient for representing the functionality of many products，users often prefer higher fidelity geometry to better understand the geometry and relationships.Rough proxies may also cause inaccurate reconstruction. Similarly，the restricted set of joint types is another limitation.In the future，we will add other primitives for part proxies，such as cylinders and spheres.We also plan to integrate more joint types between parts，such as ball joints and simple mechanical links.The current optimization framework may need to be modified to handle more geometry and joint types.Another future direction is to consider otherhigh-levelfunctionalconstraintsbetween parts.Exploring further high-level relationships could allow more sophisticated functional models.

Electronic Supplementary MaterialSupplementary material is available in the online version of this article at http://dx.doi.org/10.1007/s41095-016-0032-x.

References

［1］Han，Y.；Lee，J.-Y.；Kweon，I.S.High quality shape from a single RGB-D image under uncalibrated natural illumination.In:Proceedings of IEEE International Conference on Computer Vision，1617-1624，2013.

［2］Izadi，S.；Kim，D.；Hilliges，O.；Molyneaux，D.；Newcombe，R.；Kohli，P.；Shotton，J.；Hodges，S.；Freeman，D.；Davison，A.；Fitzgibbon，A. KinectFusion:Real-time3Dreconstructionand interactionusingamovingdepthcamera.In: Proceedings of the 24th Annual ACM Symposium on User Interface Software and Technology，559-568，2011.

［3］Shao，T.；Monszpart，A.；Zheng，Y.；Koo，B.；Xu，W.；Zhou，K.；Mitra，N.J.Imagining the unseen:Stabilitybased cuboid arrangements for scene understanding. ACM Transactions on Graphics Vol.33，No.6，Article No.209，2014.

［4］Shen，C.-H.；Fu，H.；Chen，K.；Hu，S.-M.Structure recovery by part assembly.ACM Transactions on Graphics Vol.31，No.6，Article No.180，2012.

［5］Zheng，Y.；Chen，X.；Cheng，M.-M.；Zhou，K.；Hu，S.-M.；Mitra，N.J.Interactive images:Cuboid proxies for smart image manipulation.ACM Transactions on Graphics Vol.31，No.4，Article No.99，2012.

［6］Sullivan，L.H.The tall office building artistically considered.Lippincott's Magazine 57，1896.

［7］Koo，B.；Li，W.；Yao，J.；Agrawala，M.；Mitra，N.J. Creating works-like prototypes of mechanical objects. ACM Transactions on Graphics Vol.33，No.6，Article No.217，2014.

［8］Li，Y.；Wu，X.；Chrysanthou，Y.；Sharf，A.；Cohen-Or，D.；Mitra，N.J.GlobFit:Consistently fitting primitives by discovering global relations.ACM Transactions on Graphics Vol.30，No.4，Article No. 52，2011.

［9］Lafarge，F.；Alliez，P.Surface reconstruction through point set structuring.Computer Graphics Forum Vol. 32，No.2pt2，225-234，2013.

［10］Arikan，M.；Schw¨arzler，M.；Fl¨ory，S.；Wimmer，M.；Maierhofer，S.O-snap:Optimization-based snapping formodelingarchitecture.ACM Transactions on Graphics Vol.32，No.1，Article No.6，2013.

［11］Gupta，A.；Efros，A.A.；Hebert，M.Blocks world revisited:Imageunderstandingusingqualitative geometryandmechanics.In:LectureNotesin Computer Science，Vol.6314.Daniilidis，K.；Maragos，P.；Paragios，N.Eds.Springer Berlin Heidelberg，482-496，2010.

［12］Gupta，A.；Hebert，M.；Kanade，T.；Blei，D.M. Estimating spatial layout of rooms using volumetric reasoning about objects and surfaces.In:Advances in Neural Information Processing Systems 23.Lafferty，J.；Williams，C.；Shawe-Taylor，J.；Zemel，R.；Culotta，A.Eds.Curran Associates，Inc.，1288-1296，2010.

［13］Del Pero，L.；Bowdish，J.；Fried，D.；Kermgard，B.；Hartley，E.；Barnard，K.Bayesian geometric modelingofindoorscenes.In:Proceedingsof IEEE Conference on Computer Vision and Pattern Recognition，2719-2726，2012.

［14］Jia，Z.；Gallagher，A.；Saxena，A.；Chen，T.3D-based reasoning with blocks，support，and stability.In: Proceedings of IEEE Conference on Computer Vision and Pattern Recognition，1-8，2013.

［15］Jiang，H.；Xiao，J.A linear approach to matching cuboidsinRGBDimages.In:Proceedingsof IEEE Conference on Computer Vision and Pattern Recognition，2171-2178，2013.

［16］Zheng，B.；Zhao，Y.；Yu，J.C.；Ikeuchi，K.；Zhu，S.-C.Beyond point clouds:Scene understanding by reasoning geometry and physics.In:Proceedings of IEEE Conference on Computer Vision and Pattern Recognition，3127-3134，2013.

［17］Umetani，N.；Igarashi，T.；Mitra，N.J.Guided exploration of physically valid shapes for furnituredesign.ACM Transactions on Graphics Vol.31，No.4，Article No.86，2012.

［18］Shao，T.；Li，W.；Zhou，K.；Xu，W.；Guo，B.；Mitra，N.J.Interpreting concept sketches.ACM Transactions on Graphics Vol.32，No.4，Article No.56，2013.

［19］Bokeloh，M.；Wand，M.；Seidel，H.-P.；Koltun，V.An algebraic model for parameterized shape editing.ACM Transactions on Graphics Vol.31，No.4，Article No. 78，2012.

［20］Gal，R.；Sorkine，O.；Mitra，N.J.；Cohen-Or，D.iWIRES:An analyze-and-edit approach to shape manipulation.ACM Transactions on Graphics Vol.28，No.3，Article No.33，2009.

［21］Xu，W.；Wang，J.；Yin，K.；Zhou，K.；van de Panne，M.；Chen，F.；Guo，B.Joint-aware manipulation of deformable models.ACM Transactions on Graphic Vol.28，No.3，Article No.35，2009.

［22］Daniel，M.；Lucas，M.Towards declarative geometric modelling in mechanics.In:Integrated Design and Manufacturing in Mechanical Engineering.Chedmail，P.；Bocquet，J.-C.；Dornfeld，D.Eds.Springer Netherlands，427-436，1997.

［23］Yvars， P.-A.Usingconstraintsatisfactionfor designing mechanical systems.International Journal on Interactive Design and Manufacturing Vol.2，No. 3，161-167，2008.

［24］Zhang，Q.；Ye，M.；Yang，R.；Matsushita，Y.；Wilburn，B.；Yu，H.Edge-preserving photometric stereo via depth fusion.In:Proceedings of IEEE Conference on Computer Vision and Pattern Recognition，2472-2479，2012.

［25］Rother，C.；Kolmogorov，V.；Blake，A.“GrabCut”: Interactive foreground extraction using iterated graph cuts.ACM Transactions on Graphics Vol.23，No.3，309-314，2004.

［26］Schnabel，R.；Wahl，R.；Klein，R.Efficient RANSAC for point-cloud shape detection.Computer Graphics Forum Vol.26，No.2，214-226，2007.

Yuliang Rong is currently a senior undergraduatestudentmajoring incomputerscienceatZhejiang University.Hewillworktowardsa master degree at the State Key Lab of CAD&CG in Zhejiang University after graduation.His research interests include image analysis and geometric modeling.

Youyi Zheng is currently an assistant professor at the School of Information Science and Technology，ShanghaiTech University.He obtained his Ph.D. degreefromtheDepartmentof ComputerScienceandEngineering at Hong Kong University of Science &Technology，and his M.S.and B.S. degrees from the Department of Mathematics，Zhejiang University.Hisresearchinterestsincludegeometric modeling，imaging，and human-computer interaction.

Tianjia Shao is currently an assistant researcher at the State Key Lab of CAD&CG，ZhejiangUniversity.He received his Ph.D.degree in computer science from the Institute for Advanced Study， andhisB.S.degreefrom the Department of Automation，both at Tsinghua University.His research interests include RGBD image processing，indoor scene modeling，structure analysis，and 3D model retrieval.

YinYangreceivedhisPh.D. degreeincomputersciencefrom the University of Texas at Dallas in 2013.Heisanassistantprofessor intheElectricalCommunication Engineering Department，University of New Mexico，Albuquerque，USA.His research interests include physics-based animationandsimulation，visualization，andmedical imaging analysis.

Kun Zhou is a Cheung Kong professor in the Computer Science Department of Zhejiang University，and the director of the State Key Lab of CAD&CG.Prior to joining Zhejiang University in 2008，he was a lead researcher in the Internet Graphics Group at Microsoft Research Asia.He received his B.S.and Ph.D. degrees in computer science from Zhejiang University in 1997 and 2002，respectively.His research interests are visual computing，parallel computing，human-computer interaction，and virtual reality.He currently serves on the editorial/advisory boards of ACM Transactions on Graphics and IEEE Spectrum.He is a Fellow of the IEEE.

Open AccessThe articles published in this journal aredistributedunderthetermsoftheCreative Commons Attribution 4.0 International License（http:// creativecommons.org/licenses/by/4.0/）， whichpermits unrestricted use，distribution，and reproduction in any medium，provided you give appropriate credit to the original author（s）and the source，provide a link to the Creative Commons license，and indicate if changes were made.

Other papers from this open access journal are available free of charge from http://www.springer.com/journal/41095. To submit a manuscript，please go to https://www. editorialmanager.com/cvmj.