基于三角网格表示的点云匹配算法

胡凡建

(1. 湖北第二师范学院 物理与机电学院, 武汉 430205；2. 华中科技大学 材料成形与模具技术国家重点实验室，武汉 430074)



基于三角网格表示的点云匹配算法

胡凡建1, 2

(1. 湖北第二师范学院 物理与机电学院, 武汉 430205；2. 华中科技大学 材料成形与模具技术国家重点实验室，武汉 430074)

摘要：针对传统的匹配方法收敛速度慢、对初值敏感的问题，本文提出了一种基于三角网格表示的点云匹配算法。该算法主要包括两个步骤：首先，采用主成份分析对点云进行整体分析，通过奇异值分解计算初始变换参数；然后，采用螺旋运动理论在三角网格模型中定义点-切面距离以构造目标函数，并通过求解一个线性方程组计算最优刚体变换参数。实验结果证明了本文所提算法的有效性。

关键词：匹配；刚体变换；主成份分析；螺旋运动

近年来，高精度的接触式或非接触式测量方法在汽车覆盖件、航空发动机叶片等曲面类零件的加工制造中广泛应用。然而，受测量设备自由度和视场限制，需多次测量才能获取整体数据。点云匹配目的就是计算三维空间的刚体变换参数，将不同坐标系下的点云数据统一到同一平台下。点云匹配(也称对齐或拼合)技术在逆向工程、曲面寻位、质量检测和文物保护等领域均有着广泛应用，已成为这些领域的研究热点也是难点问题之一。

点云匹配可分为粗匹配(Coarse Registration)算法和精匹配(Fine Registration)算法两类[1]。粗匹配利用曲面特征构造几何不变量，在不同视图搜索对应点完成匹配。Johnson和Hebert[2]提出了Spin-Image方法，利用法线距离和切平面距离构造了二维几何不变量；斯坦福大学的Gelfand等[3]构造体积不变量解决米开朗琪罗工程中的匹配问题；Masuda使用局部高度映射构造了LPHM搜索对应点[4]。上述粗匹配算法需对目标视图中的所有点构造不变量，匹配效率较低。近年来，Yamany[5]、Maekawa[6]、孙玉文[7]、刘宇[8]等学者提取微分信息构造不变量。然而微分信息对噪声敏感，处理由许多相似区域构成的曲面时，会产生多重对应，导致匹配失败。

ICP算法(Iterative Closest Point)[9]及其改进算法[10]是目前应用最广泛的基于迭代策略的精匹配算法。该算法定义点-点欧式距离作为目标函数，通过奇异值分解得到最大特征值对应的特征向量计算旋转变换参数，进而由质心坐标计算平移变换参数。ICP算法无需构造几何不变量，线性收敛于局部最优解，其主要缺点是收敛速度慢，收敛精度与初值有关。从几何优化的角度，Pottmann等[11]提出了TDM(Tangent Squared Distance Minimization)和SDM(Squared Distance Minimization)算法。TDM算法使用点-切面距离构造目标函数，由于无需计算曲率值，相比SDM算法应用更为广泛。Pottmann等证明了TDM算法比ICP算法收敛速度快，但对初值非常敏感。当点云相距较远时，算法易陷入局部最优甚至发散。此外，Chow[12]、Salvi[13]等提出了基于遗传方法的精匹配算法，尽管该类方法对初值无要求，但计算效率低。

在上述工作的基础上，本文提出了一种基于三角网格表示的匹配算法。本算法包括两个主要步骤：首先，使用主成份分析(PCA：Principal Component Analysis)获取移动视图与目标视图的笛卡尔坐标系统，计算初始旋转变换和平移变换参数；然后，在网格曲面上定义点-切面距离，由螺旋运动理论将匹配问题定义为非线性最小二乘问题，并通过求解线性方程组计算最优刚体变换参数。

1初始刚体变换参数的计算

1.1数据预处理

为了提高三角网格的质量，在匹配前需对直接测量的数据进行预处理。点云数据预处理的内容包括去除噪声、修补空洞、网格三角化和网格细分等。对于粗大噪声，可在商业化软件(如Geomagic、Polyworks等)中由人工交互直接去除。对于高斯噪声、空洞和稀疏网格，可使用Geomagic软件中相应模块进行操作。将处理后的网格曲面存为PLY文件，以便于不同软件平台中的转换和传输。PLY文件格式是美国斯坦福大学开发的数据存储格式，图形学领域很多著名的模型 (如兔子、米开朗琪罗和中国龙等)均采用该格式存储。

1.2曲面PCA

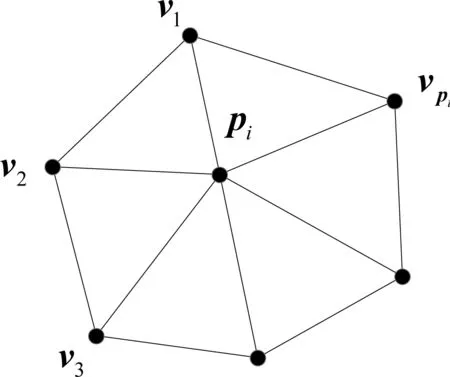
图1　在三角网格中计算权重系数

定义移动点云P={p1,p2,…,pnp}、目标点云Q={q1,q2,…,qnQ}。如图1所示，对于网格曲面P中任意pi，定义环绕pi点一周内的三角形顶点为Vi={v1,v2,…,vni}，三角形Fi={f1,f2,…,fni}的面积分别为{a1,a2，…,ani}。计算P的质心μP及坐标差pi

pi=pi-μp

(1)

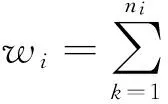
(2)

对矩阵Hp进行奇异值分解，得

(3)

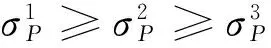
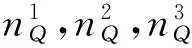
(4)

式中R0∈R3×3,(R0)T=(R0)-1,det(R0)=1。进而求解初始平移变换参数

t0=μQ-RμP

(5)

式中t0∈R3。求得的刚体变换参数g0=(R0,t0)可作为下节精匹配的初始值，由迭代策略进一步计算最优刚体变换参数。需要特别指出的是通过本节方法计算初始变换参数时，只需构造一个协方差矩阵，由奇异值分解计算正交单位矢量。不需要对移动点云中所有点构造几何不变量，同时也不需要定义严格的相似性度量指标，计算简单。

2基于螺旋运动的精匹配算法

任何物体从一个位姿到另一个位姿的运动都可以表示为绕某直线的转动和沿此直线移动的复合实现，这种复合运动称为螺旋运动，因此，刚体变换参数可由螺旋运动表示和求解。本节将提出一种基于螺旋运动的精匹配算法-ScrewMotion-basedFineRegistration(SMFR)。

2.1螺旋运动基础

定义单参数螺旋运动坐标系为∑P/∑Q，则

pi(t)=R(t)pi+t(t)

(6)

上式表示在时刻t，将移动坐标系∑P中的点pi映射到目标坐标系∑Q中。∑P中所有的点在∑Q有一条路径曲线，该曲线的原点为pi，曲线形状由变换参数R(t),t(t)控制。对式(6)求导，得

v(pi)=R(t)pi+t(t)

(7)

v(pi)表示t时刻点pi在∑Q中描述的速度矢量。对式(7)进行线性化表示[14]，可得

(8)

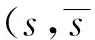
pi=pi+v(pi)

(9)

(1) 如果l=0，则该运动为平移运动；

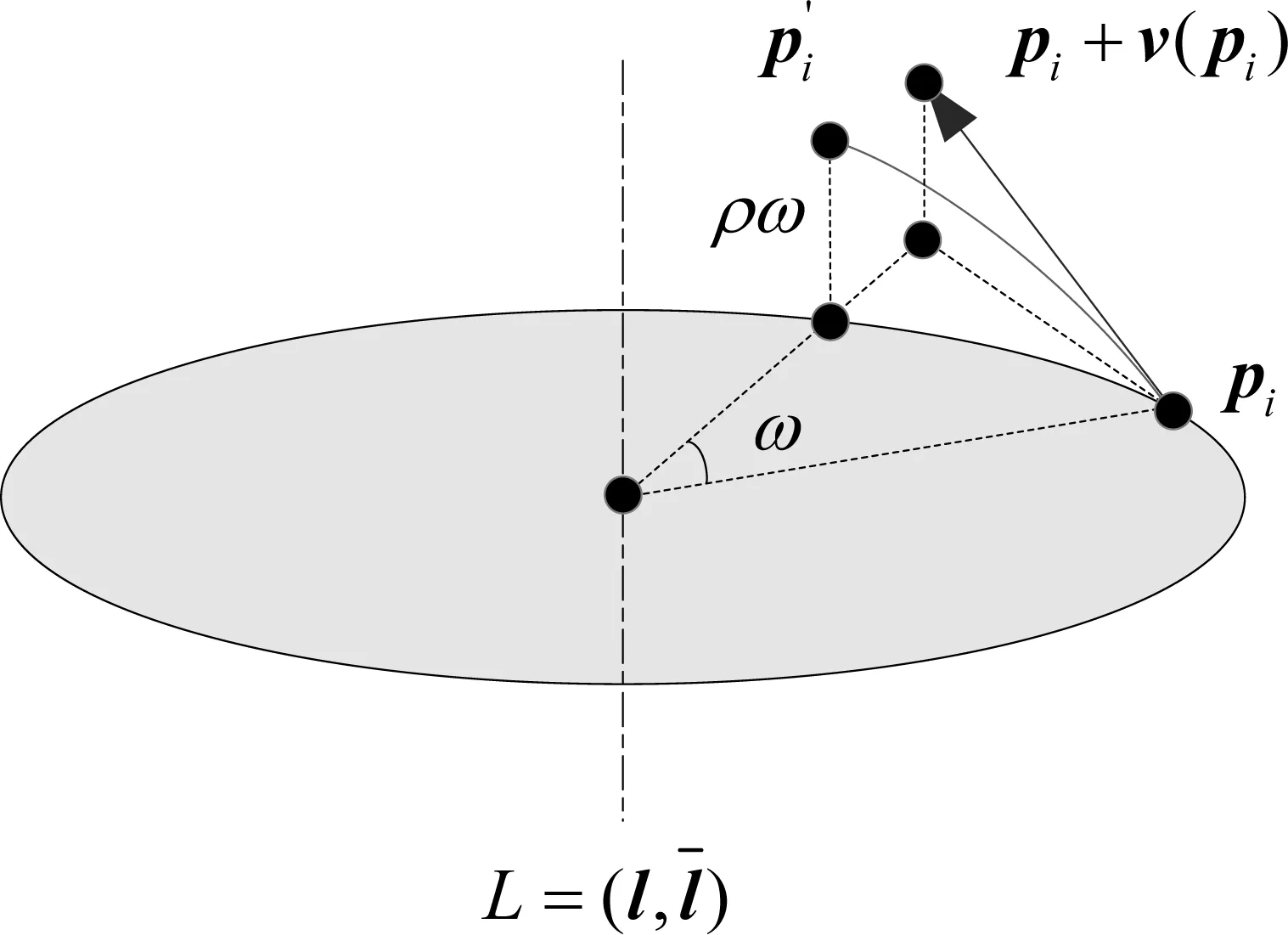
图2　 瞬时螺旋运动中的几何量,其中点位置由线性拟合得到

2.2目标函数定义

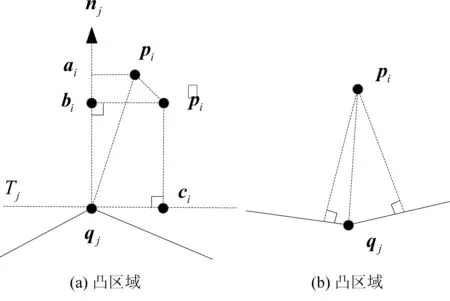
图3　点-切面距离误差定义

如图3(a)所示，对于∀pi∈P，在目标点云Q搜索其距离最近点qj，满足

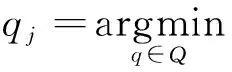
(10)

由于网格曲面中含有三角形曲面片的方向矢量，点qj处的法向矢量nj由下式拟合

(11)

式中，ak表示环绕pi点三角形曲面片的面积，nk表示对应三角形的法矢。测量的离散数据具有一定的采样分辨率，大多数情况下点pi不在nj上，所以点pi到切平面Tj的距离为jj(pi-qj)。经过空间运动后，pi点位置变为pi，此时点-切面距离为

(12)

考虑到pi点的影响程度，引入权重系数定义精匹配算法的目标函数

(13)

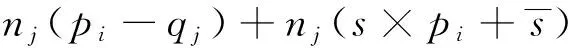
2.3变换参数求解

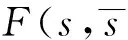
(14)

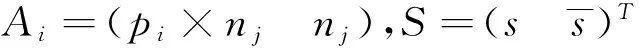
=C+2BTS+STAS

(15)

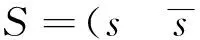
AS+B=0

(16)

在微分运动条件下，刚体变换参数由下式决定[14]

(17)

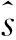
3计算复杂度分析

本文所提出的点云匹配算法整体步骤如下：

(1) 求解初始变换矩阵g0=(R0,t0)，完成移动点云P同目标点云Q的初步匹配。

(a) 查询围绕点pi的曲面片，计算权重系数wi；

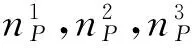
(c) 根据式(4-5)，计算初始旋转变换参数R0和平移变换参数t0。

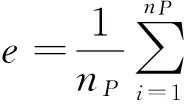
(a) 更新pi点位置，对于∀pi∈P搜索最近点qj；

(b) 查询围绕点qj一周的三角形面片，确定法矢量nj；

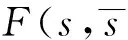
(d) 求解式(16)中线性方程组计算变量S，按式(17)计算刚体变换参数g=(R,t)；

(e) 分析是否满足终止条件，如果满足则输出最优刚体变换参数g*=(R*,t*)；否则转(2-a)循环。

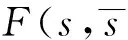
4实验结果

为了验证本文所提算法的有效性，采用具有复杂曲面特征的壳体零件为例进行仿真实验。移动点云P采用Salvi的方法[1]由Q沿坐标轴旋转和平移产生，旋转角度和平移距离分别为45°、3mm。为了测试算法对噪音的鲁棒性，在点云数据中加入了高斯噪音N(0.05,0.01)2，同时在移动点云中去除1/5左右的数据。仿真实验结果见图4和图5，从实验结果可以看出在所有测试算法中PCA+SMFR算法是收敛速度最快且匹配精度最高的。在初值较差的情况下，使用点-点距离的ICP算法经过20步迭代后均值误差仍没有达到稳定值。本文所提算法首先使用PCA计算一个初始变换参数，在此初值下使用SMFR在5步迭代内快速达到最优值。

本实验使用PCA+SMFR算法后获得的最终刚体变换参数和均值误差见表1。尽管跟ICP算法具有相似的计算复杂度，但由于PCA+SMFR算法收敛速度快，获得最优刚体变换变换参数的计算耗时远小于ICP算法。

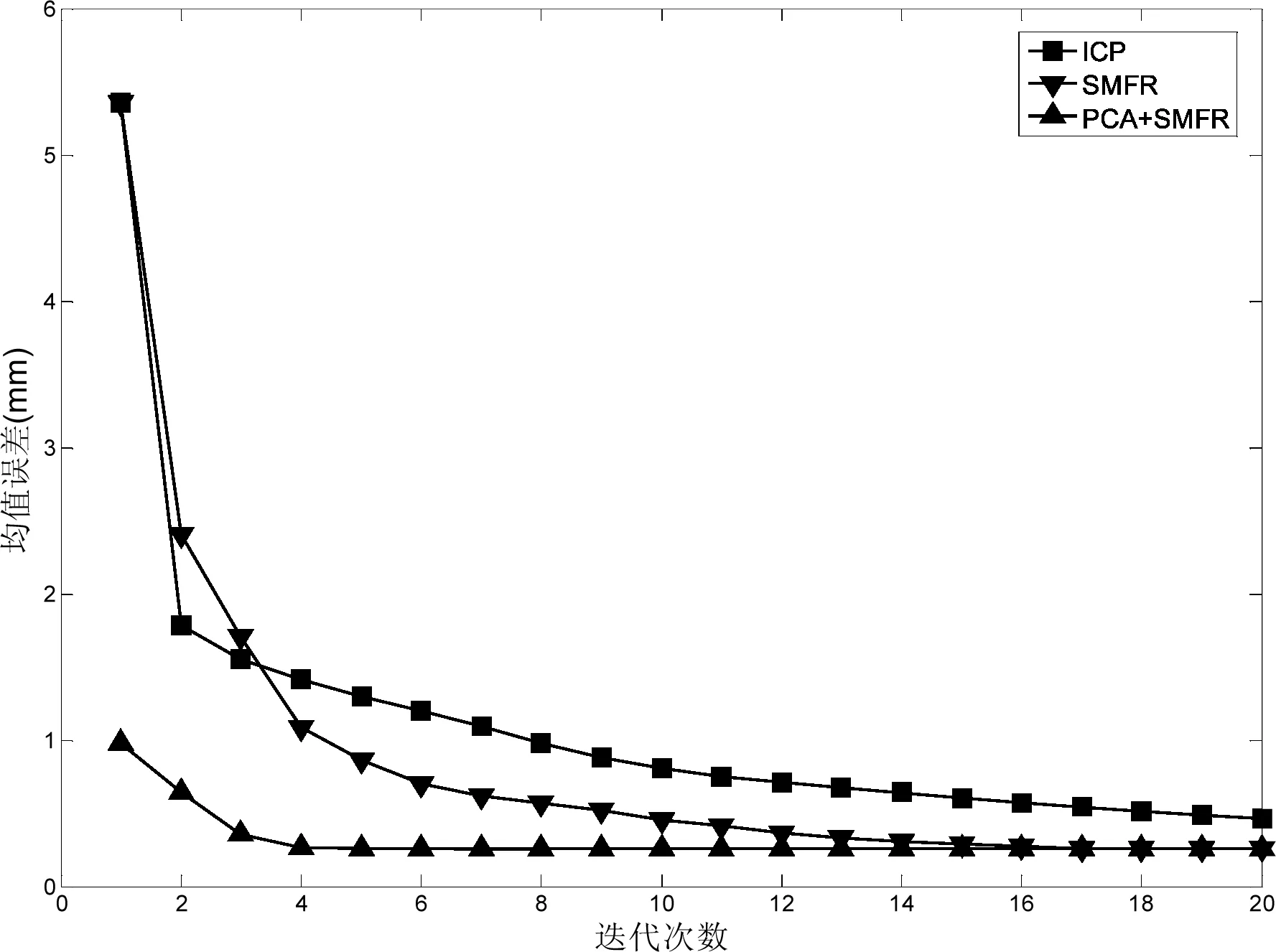
图5　使用壳体模型比较均值误差

粗匹配精匹配旋转参数R0.4646-0.10580.87920.59470.7729-0.2213-0.65610.62570.4220æèçöø÷0.4938-0.17360.85210.51130.8505-0.1230-0.70340.49640.5087æèçöø÷平移参数t(4.2831,6.0692,5.4735)(4.8251,5.0732,4.9486)均值误差(mm)0.98250.2613

5结论

(1) 提出了一种基于三角网格表示的点云匹配算法。该算法首先执行PCA完成初始匹配，然后执行SMFR计算最优刚体变换参数。使用主成份分析快速计算出初始旋转变换参数，解决了精匹配算法对初值敏感的问题。此外，该算法不需要重新计算法矢、曲率等微分信息，稳定性好。

(2) 分析了本文所提算法的计算复杂度，并通过仿真实验验证了算法的匹配效率和精度。实验结果表明，本文所提算法比ICP更快的收敛于最优解，快速准确的完成了移动点云与目标点云的匹配任务。

(3) 需特别指出的是本文所提算法使用条件同ICP相似：要求移动点云为目标点云的子集。当该条件不成立时，可先由Huber和Hebert[15]的方法查询重叠区域后，再使用本文所提算法进行匹配。

参考文献:

[1]SALVI J, MATABOSCH C, FOFI D, et al. A review of recent range image registration methods with accuracy evaluation[J]. Image and Vision Computing, 2007, 25(5): 578-596.

[2]JOHNSON A E, HEBERT M. Surface matching for object recognition in complex three-dimensional scenes[J]. Image and Vision Computing, 1998, 16(9-10): 635-651.

[3]GELFAND N, MITRA N J, GUIBAS L J, et al. Robust global registration[C].Proceedings of the Symposium on Geometry Processing, 2005, Vienna, Austria: 197-206.

[4]MASUDA T. Log-polar height maps for multiple range image registration[J]. Computer Vision and Image Understanding, 2009, 113(11): 1158-1169.

[5]YAMANY S M, FARAG A A. Surface signatures: An orientation independent free-form surface representation scheme for the purpose of objects registration and matching[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(8): 1105-1120.

[6]KO K H, MAEKAWA T, PATRIKALAKIS N M. An algorithm for optimal free-form object matching[J]. Computer-Aided Design, 2003, 35(10): 913-923.

[7]徐金亭, 孙玉文, 刘伟军. 复杂曲面加工检测中的精确定位方法[J]. 机械工程学报, 2007, 43(6): 175-179.

[8]刘宇, 熊有伦. 基于法矢的点云匹配方法[J]. 机械工程学报, 2007, 43(8): 7-11.

[9]BESL P J, MCKAY H D. A method for registration of 3-D shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239-256.

[10]LIU Y. Improving ICP with easy implementation for free-form surface matching[J]. Pattern Recognition, 2004, 37(2): 211-226.

[11]POTTMANN H, HUANG Q-X, YANG Y-L, et al. Geometry and convergence analysis of algorithms for registration of 3D shapes[J]. International Journal of Computer Vision, 2006, 67(3): 277-296.

[12]SILVA L, BELLON O R P, BOYER K L. Precision range image registration using a robust surface interpenetration measure and enhanced genetic algorithms[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(5): 762-776.

[13]CORDON O, DAMAS S, SANTAMARIA J. A fast and accurate approach for 3D image registration using the scatter search evolutionary algorithm[J]. Pattern Recognition Letters, 2006, 27(11): 1191-1200.

[14]熊有伦, 尹周平, 熊蔡华, 等. 机器人操作[M]. 武汉: 湖北科学技术出版社, 2002.

[15]HUBER D. F., HEBERT M. Fully automatic registration of multiple 3D data sets[J]. Image and Vision Computing, 2003, 21(7): 637-650.

A Registration Algorithm For Point Clouds Based on The Triangular Representation

HU Fan-jian1,2

(1. Hubei University of Education, Wuhan 430205, China;2. State Key Laboratory of Materials Processing and Die & Mould Technology,Huazhong University of Science & Technology, Wuhan 430074, China)

Abstract:This paper proposes a novel registration algorithm based on the triangular representation, aiming to handle the problems of slow convergence and existing sensibility to initial value in traditional algorithms. The proposed algorithm consists of two major steps: First, Principal Component Analysis is used to analyze the data, then the Singular Value decomposition is used to calculate the initial transformation parameters; Second, the theory of screw motion is employed to define the point-tangent distance in triangles in order to construct the objective function which is calculated to obtain the optimal rigid transformation parameters by solving a series of linear systems. The validity of the proposed algorithm is verified by the experiment.

Key words:matching; rigid transformation; principal component analysis; screw motion

收稿日期：2016-01-10

作者简介：胡凡建(1981-)，男，湖北咸宁人，博士研究生，研究方向为材料加工工程。

中图分类号：TH14

文献标识码：A

文章编号：1674-344X(2016)02-0016-06