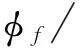基于动态信息的级联失效负载重分配策略*

李从东　邓原　原智峰　王玉

(暨南大学 管理学院, 广东 广州 510632)



基于动态信息的级联失效负载重分配策略*

李从东邓原†原智峰王玉

(暨南大学 管理学院, 广东 广州 510632)

摘要:为解决级联失效网络负载重分配问题,提出了一种将网络局部信息和动态信息相结合的负载动态重分配策略.该策略根据节点的度与节点实时处理能力计算节点权重,并以此依次进行负载重分配;同时,按一定比例选取失效节点暂停工作,其负载重新分配进程相应停止.在BA无标度网络、WS小世界网络和ER随机网络上的仿真结果表明,在一定的参数条件下,相对于介数分配策略与度数分配策略,动态重分配策略通过降低网络整体负载率、优化网络实时流分布缓解级联失效的效果更为明显.

关键词：级联失效;Motter和Lai 模型;动态重分配策略;复杂网络

网络化系统的相互关联与耦合增加了故障扰动的可能性与传播速度[1].微小的、局域的随机扰动或失效通过级联机制,可以对整个网络产生较大的影响,甚至导致系统全局崩溃[2- 4].一个节点的失效会导致网络负载的重新分配,负载的重分配又使得某些节点上的负载超过其负载容量而失效,产生连锁反应,最终导致一部分节点甚至整个网络的崩溃[5].

近年来,级联失效得到了广泛的研究.Motter等[6]提出了负载容量线性模型,并通过调整容忍参数μ对复杂网络上级联失效的破坏程度进行了分析.Holme等[7- 8]对网络中节点和连边因过载而引发的级联传播动态过程进行了仿真分析.Crucitti等[9]通过重点保护网络中度大的节点或介数较大的节点以及调整网络中的流量分布来缓解级联失效对网络的影响.王建伟等[10]针对以介数为负载重分配依据而存在耗时且计算复杂的情况,提出了一种带有可调参数的相继故障模型,并以节点度为依据进行负载重新分配.李涛等[11]针对无标度网络提出了整体传输优化方法.段东立等[12]针对级联失效中的过载机制,对网络节点重要度的动态演化机理进行了分析.然而,现有研究仍需进一步考虑两个问题:①现有负载重分配策略是基于网络拓扑结构的静态信息(如节点的介数或度数),未能有效地体现网络中流的动态过程,特别是级联失效中的过载机制;②负载分配策略以失效节点移除或预移除为主要缓解手段,这种分配策略未考虑真实网络系统中存在允许失效节点暂时失去功能但其负载不重新分配而是待节点功能恢复后再处理的情况.

为此,在文献[12]对过载机制分析的基础上,文中结合网络节点负载实时动态信息,提出了一种负载动态重分配策略.在该策略中,根据节点的度与节点实时处理效率计算节点的权重,按节点权重从高到低的排序进行负载分配;同时选取一定比例的失效节点暂停工作,待其功能恢复后自行处理负载,以此构建模型并在BA无标度网络、WS小世界网络和ER随机网络上进行仿真分析.

1级联失效模型

根据网络负载及流量分布和Motter等[6]的ML负载容量模型,文中提出了反映网络实时动态信息和级联失效之间关系的级联失效模型.实时动态信息主要是指节点与边的负载率,随着物联网技术的应用,利用此类信息的成本有所降低,数据获取速度的提高可以显著延缓拥塞而提高网络的传输性能.为了获取网络实时状态信息,一般网络每隔若干个时间单位更新一次动态负载信息,以负载与容量的比值来表示节点与边的实时负载率.

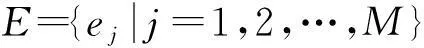
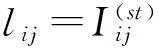
(1)

假设网络节点收、发流量是同步的,源节点将流量实时发送到网络上.任一源节点可在N-1个节点中任意选择一个节点作为汇节点,负载量可以视为在某一时刻任意节点或边上实时流量的总和,两者关系如下:

(2)

考虑到节点与边同时存在相对方向的流量,为不失一般性,式(2)中采用绝对值来体现节点与边的实时负载量,避免出现相对方向流量正负抵消的情况.

需要说明的是,为刻画网络整体源、汇节点的传输关系以及负载量与流量输入、输出关系,文中将节点vi与边eij的实时负载由通过该节点或边的网络中所有源、汇节点之间的实时传输流量决定.节点的负载量不能超过其最大设计容量,当节点实时负载量超过其最大设计容量时,停止接收新的流量.

文中以CL模型(C=(1+μ)L)[14]为基础,即负载是时变值,节点与边的负载容量关系为

(3)

式中，Li(t)和Lij(t)分别为节点vi与边eij在t时刻的负载量,Ci和Cij分别为节点vi与边eij的设计最大容量[15- 16],α为可调节容量参数,0<α<1.

加入节点负载信息以反映网络实时传输效率,以节点及边的实时负载量为动态信息,记wi和wij分别为节点vi与边eij的实时负载率,则

(4)

衡量节点vi实时处理负载能力的强度指标Pi为

(5)

式中,Ai为节点vi的设计容量占网络节点设计总容量的比值,即该节点负载处理能力的总体贡献度.

2负载分配策略及流程

2.1负载分配策略

现有负载分配策略多以介数或度数作为负载重新分配的依据,即介数或度数越高的节点越优先分配负载,实际上是以节点在网络中的位置为主要考虑因素.考虑到引起级联失效的主要原因是网络流量分布不均,局部节点失效导致网络整体传输效率降低,而随着失效节点负载的重新分配,因级联效应，局部拥塞被放大导致网络整体传输能力降低,仅考虑节点位置中心性而不考虑节点负载处理能力的分配策略,将会使处于中心位置的节点因承受更大的压力而提高级联失效发生的可能性,不利于缓解网络拥塞.同时,现有策略多以移除或预移除失效节点,并将其负载重新分配为原则,实际上是通过节点移除改变了网络结构后再进行负载分配,这与真实网络系统情况有一定的差别.如航空网络中某些航线不能正常工作时,其客流并不立即分配到其他航线,而是等待航线恢复或选择其他方式;电网中发电站或电路出现失效时,局部停电待修更为常见[15].

因此,文中结合网络拓扑结构信息、节点邻域信息及网络实时信息构建负载动态分配策略.当发生级联失效时,按比例f(0≤f≤1)选取失效节点并暂停其功能,其负载不进行重分配,直到级联失效过程停止后再恢复其功能并进行负载转移,其余1-f的失效节点进行负载移除,其负载按失效节点的相邻节点的实时处理能力P(见式(5))进行排序,并依次重新分配.当某个节点对vij失效被移除时,节点vi上的负载将重新分配至其相邻节点[16- 17],相邻节点vj收到额外负载量为

(6)

式中,Γi为节点vi的相邻节点集合.对于节点vj而言,当Lj+ΔLj>Cj时,因负载量超过容量而失效,其负载再次分配到相邻节点上,级联失效过程继续,直至重新分配后网络内任意节点vm的负载量Lm+ΔLm≤Cm时,级联过程终止.2.2负载分配流程

1)若t0时刻节点vi的负载量大于其容量,即Li(t)>Ci,则节点vi处于失效状态.

2)t1时刻将节点vi的负载向外分配,根据t0时刻其相邻节点的实时处理能力P(见式(5))对节点负载进行排序,根据排序情况对失效节点vi的负载量Li(t)进行均匀分配,即依据各个节点的t0、t1权重值顺序分配到各个节点上.

3)在t2时刻若节点vi的负载已分配完毕,并且所有接受负载的节点在t1时刻的流量不超过其容量,则完成分配,级联失效过程停止,节点vj收到分配来的负载量后按照连边的负载率即wjh进行降序分配,否则返回步骤2).

3仿真实验

3.1仿真模型及分析指标

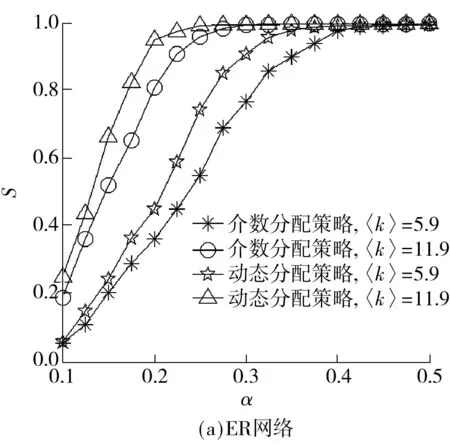
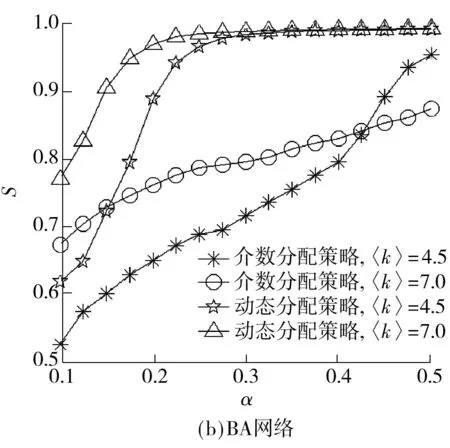
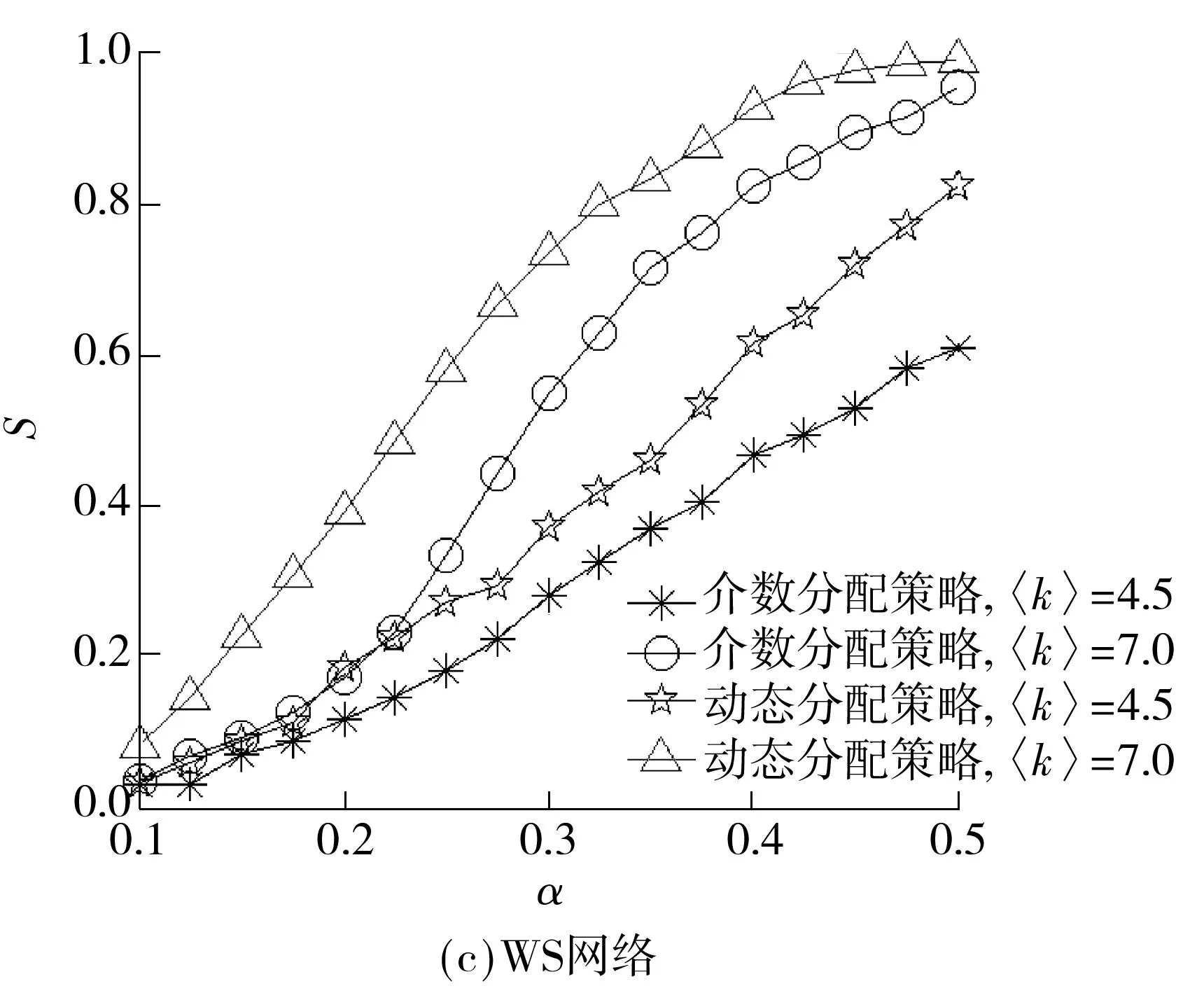
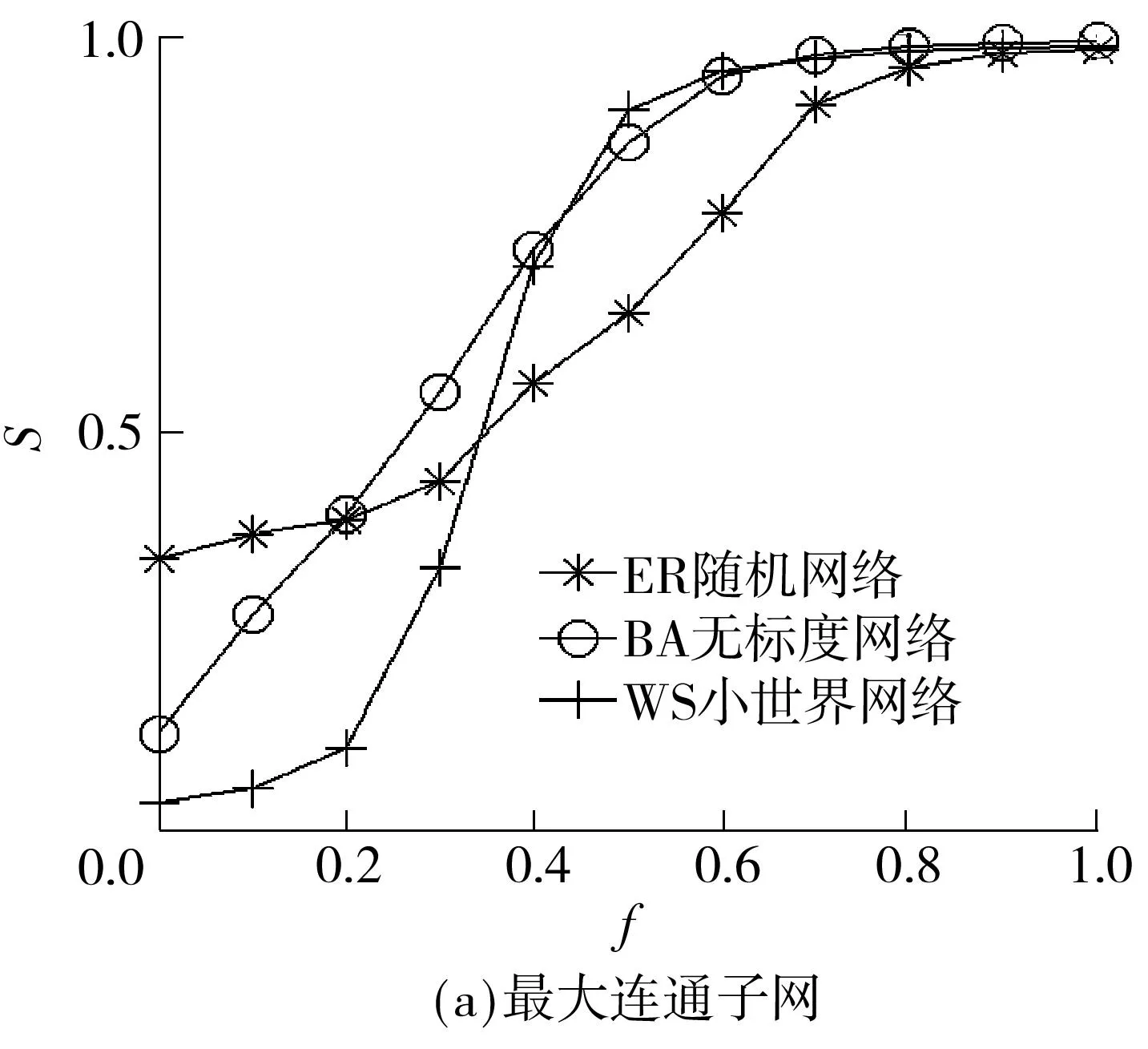
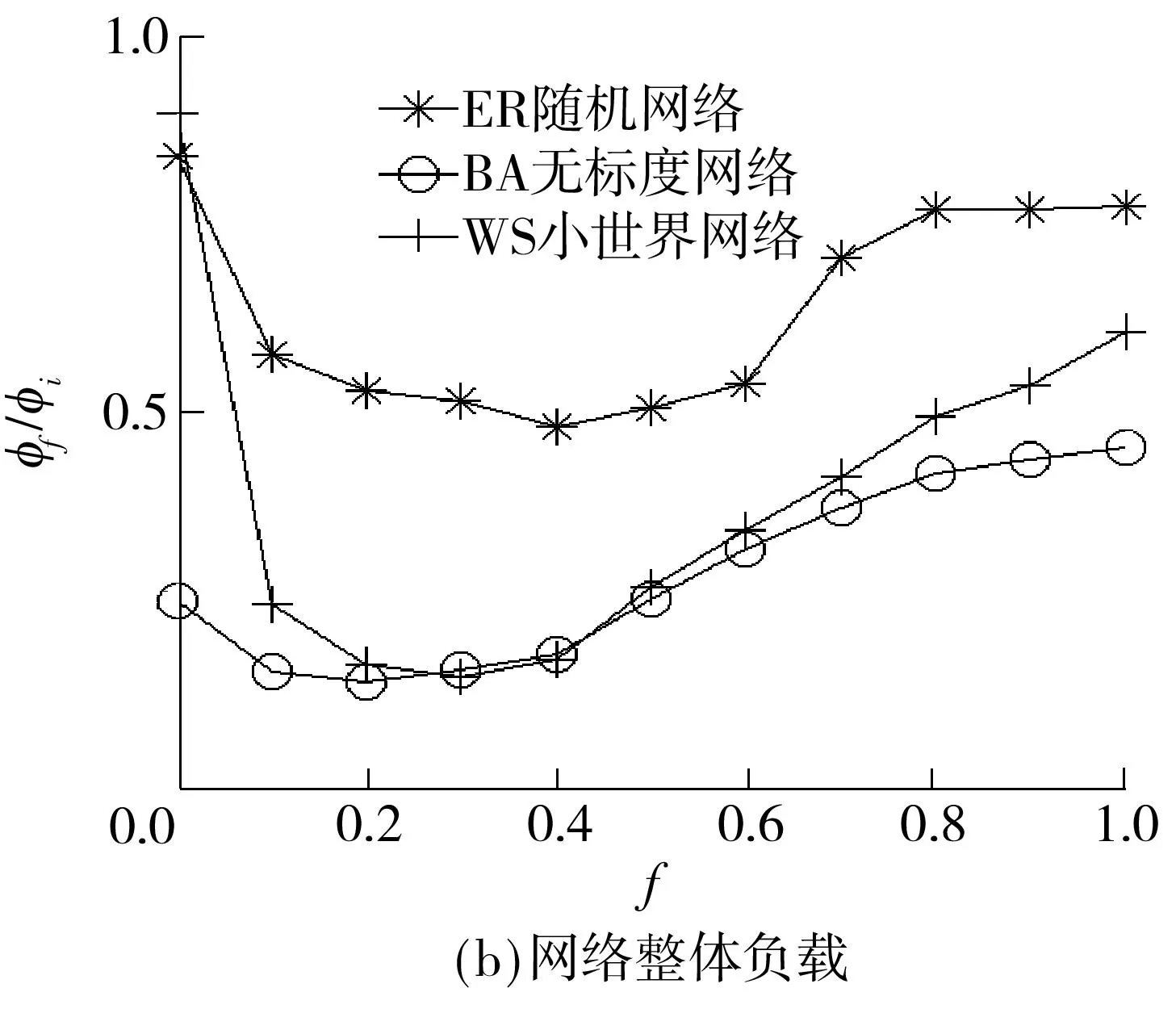
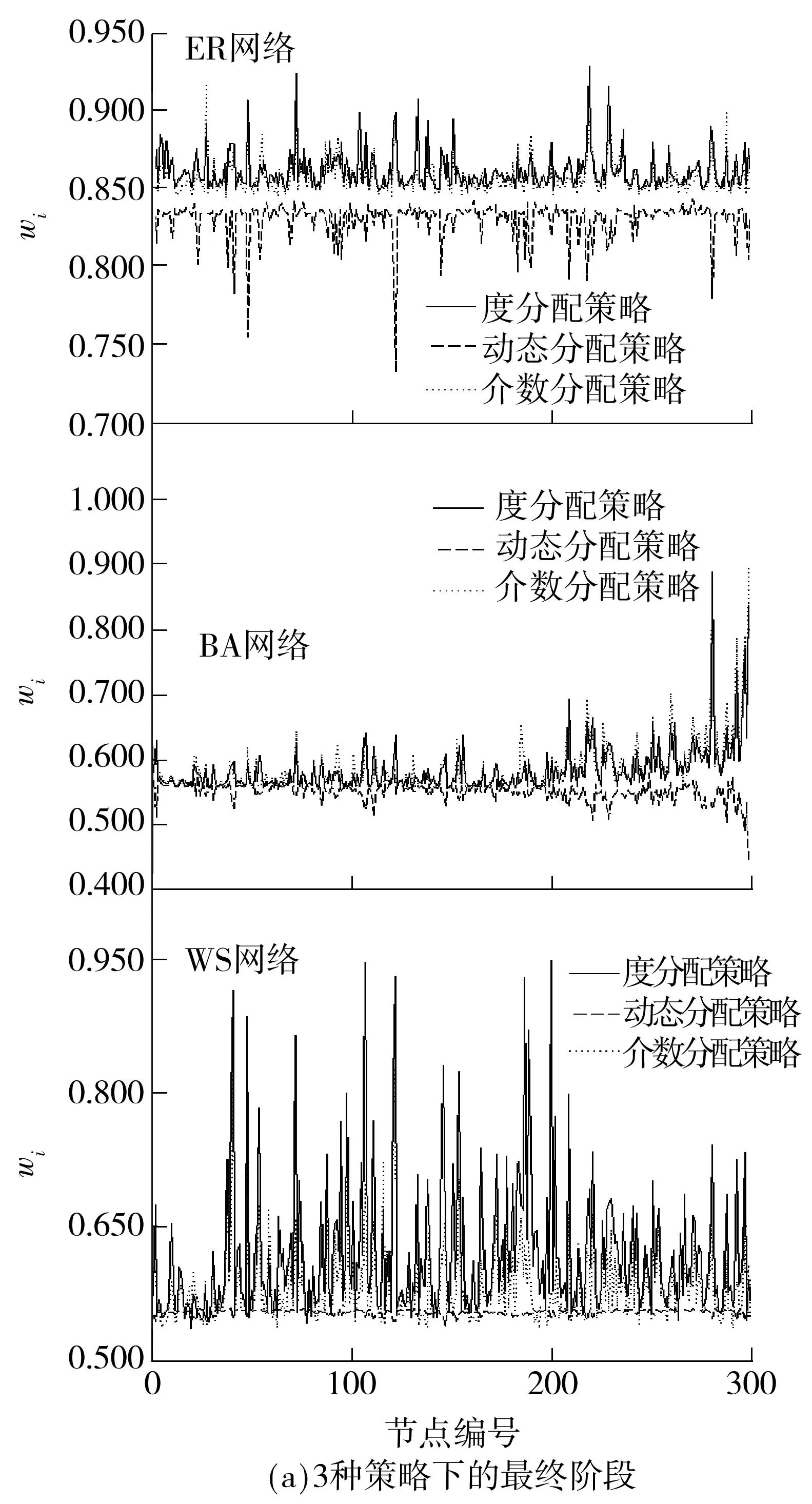
为探讨介数分配策略、度分配策略以及动态分配策略的特点,以网络节点数N=300、网络平均度〈k〉在 1.5至15.0之间、300次迭代模拟了级联失效过程,测试了失效节点部分移除、部分暂停的情况.仿真网络模型为ER随机网络、BA无标度网络、WS小世界网络.ER随机网络模型的生成方法为[15]:给定网络节点总数N,在每一时间步任意选择两个节点,以概率p=2m/[N(N-1)]连边,其中m是给定的总边数,m

文中采用的分析指标包括:

(1)级联失效后最大连通子网规模

S=N′/N

(7)

式中,N′为级联失效后保持连通尺寸的最大节点数,N为原网络中的节点数.S越大表明级联失效后最大连通子网的规模越大,网络的连通能力越强.

(2)网络整体负载.网络实时整体传输效率为t时刻网络节点vi的最大负载量与设计容量的比值,即

φi=max(wi)=maxi{li(t)/Ci}

(8)

级联失效后,在对比例为f的失效节点不进行移除的情况下,最大连通子网的节点最大实时负载率为

φf=maxf(lj(t)/Cj)

(9)

其中,网络节点最大实时负载率越高,表示网络整体传输效率越低.φf/φi表征不移除策略对网络整体传输效率的优化作用.

(3)网络局部负载分布.通过测试节点运行效率wi(t)的分布情况来考察不同分配策略对节点实时负载率分布的影响,比较策略对局部负载的优化效果.

3.2仿真结果与分析

3.2.13种策略在不同类型网络中的应用

ER网络的仿真结果如图1(a)、1(b)所示,对于发生级联失效后的最大连通子网规模,运用度分配策略和介数分配策略的效果接近,动态分配策略优于前两种分配策略.由于ER网络的节点分布均匀,当α>0.30时网络容量明显大于网络负载量,发生级联失效的可能性较低,故3种策略的最大连通子网规模的差距并不明显;如图1(b)所示,当α>0.075时,动态分配策略的最大连通子网规模逐渐优于其余两种策略,α=0.16时3种策略的最大连通子网规模的差距最大;当α>0.16时,网络整体负载量相对降低,不同策略之间的最大连通子网规模的差距逐渐缩小.BA网络的仿真结果见图1(c):当0<α<0.70时,动态分配策略的最大连通子网规模优于其他两种策略;当α>0.70时,网络整体负载量相对降低,不同策略之间的最大连通子网规模的差距逐渐缩小.WS网络的仿真结果见图1(d),当0<α<1时动态分配策略的最大连通子网规模优于其余两种策略,且当α>0.60时网络整体负载能力的提高,使不同策略之间的最大连通子网规模的差距逐渐缩小.

图1　不同网络下3种策略的最大连通子网规模

综上所述,当ER网络的α>0.16,BA网络的α>0.70,WS网络的α>0.60时,3种策略的最大连通子网规模的差距开始缩小,应采用成本最小的策略.

由于以上测试经过迭代,结果受网络整体结构性质的平均影响,因此在不同参数情况下将介数分配策略与动态分配策略做进一步测试,考察两者基于节点局部信息下的缓解表现,结果如图2所示.从图中可知,在随机设置不同平均度条件下,动态分配策略的最大连通子网规模均大于介数分配策略,即在局部发生拥塞的情况下,动态分配策略对提高网络传输能力的作用优于介数分配策略.

进一步从网络拓扑结构的角度对仿真结果进行分析[19],ER和WS网络的度分布分别为泊松分布、近似于泊松分布,这两类网络的绝大部分节点的度分布在平均度附近,呈现出某种“均质性”,网络平均连通度较高,节点负载量与节点度正相关,ER、WS网络的负载量也呈现出“均质性”;BA无标度网络的节点度呈幂律分布,网络内呈现出“异质性”,即少数中心节点的连通程度高,此类节点的容量高并承载着较高的负载,而大量非中心节点的连通程度低,容量和负载也相应较低.基于节点处理能力的动态分配策略考虑了局部负载不平衡现象,在综合节点度信息的基础上按照相邻节点的实际处理能力分配负载量,有效地缓解了位于局部中心位置(度中心)的相邻节点因重分配而引发新一轮过载的情况;在介数分配策略下,由于BA网络中少数中心节点同时也是介数中心,ER与WS网络的介数分布范围较窄,若负载重分配策略仍依据节点介数信息,则无疑是加重了少数中心节点的负载分配量,提高了中心节点过载的可能性,从而扩大网络级联失效的范围.因此,从整体上动态分配策略在降低局部网络负载方面优于其他两种策略.

3.2.2f对缓解级联失效的作用分析

图2　不同平均度和网络下两种策略的最大连通子网规模

图3　f对缓解级联失效的作用

3.2.3网络局部负载分析

不同策略下ER、BA、WS网络节点负载分布如图4(a)所示,采用动态分配策略时3种网络在级联失效最终阶段的节点负载比其他两种策略小.

BA网络的幂律分布特性使不同策略下的节点最终负载分布也具有幂律分布特征.采用介数和度分配策略时,处于网络中心位置的节点负载非常高,这是由网络结构决定的.采用动态分配策略时,位置中心性对负载重新分配不是决定性因素,因此处在中心位置的节点负载相对其他两种策略较低.

受WS网络随机跳跃重连边的影响,采用度分配策略和介数分配策略时,网络平均集聚系数和平均距离会受到随机影响,导致节点负载分布更加不均衡.动态分配策略能避免结构变动造成的网络负载分配不均衡的情况,有效地减少网络节点负载率,使节点间的负载分布更加均匀.

采用动态分配策略时,3种网络在级联失效的第一和最终阶段的节点负载分布相对均匀、峰值显著降低,如图4(b)所示.这与前面的仿真分析结论一致,体现了动态分配策略对调节网络节点负载的优化作用.

图4不同网络的负载分布仿真结果

Fig.4Simulated results of different network load distribution

4结论

通过仿真测试发现,在不同网络结构、不同参数下,介数分配策略、度分配策略与动态分配策略各有侧重,总的来说,动态分配策略对缓解级联失效有明显优势.通过选取一定比例失效节点不予移除、其负载量不对外分配的方式,对节点按照实时负载处理能力和度数共同排序并依序进行负载重分配,动态分配策略能有效地降低网络整体负载率、优化网络节点负载率分布,对由于网络流量动态变化与网络节点容量有限引发的级联失效有较强的针对性.

后续将进一步探讨以下几个问题:①移除与暂停节点选择标准(如随机选取、特定选取及实时信息更新时间间隔等)对策略的影响;②在网络连接方式、结构、层次以及节点性质出现变化时,策略的适应性改进;③结合真实网络数据构建算法,特别是在多目标规划下,如何在尽可能短的时间内得出全局最优解或策略.

参考文献：

[1]OUYANG M.Review on modeling and simulation of interdependent critical infrastructure systems [J].Reliability Engineering & System Safety,2014,121:43- 60.

[2]GONG M,MA L,CAI Q,et al.Enhancing robustness of coupled networks under targeted recoveries [J].Science Report,2015,5:8439/1- 7.

[3]GAO J,BULDYREV S V,HAVLIN S,et al.Robustness of a network of networks [J].Physical Review Letters,2011,107(19):195701/1- 5.

[4]BARTHéLEMY M.Spatial networks [J].Physics Reports,2011,499(1):1- 101.[5]WANG W X,CHEN G.Universal robustness characteristic of weighted networks against cascading failure [J].Physical Review E:Statistical,Nonlinear and Soft-Matter Physics,2008,77(2):026101/1- 5.

[6]MOTTER A E,LAI Y.Cascade-based attacks on complex networks [J].Physical Review E:Statistical,Nonlinear,and Soft-Matter Physics,2002,66(6):065102/1- 4.

[7]HOLME P,KIM B J.Vertex overload breakdown in evolving networks [J].Physical Review E:Statistical,Nonli-near,and Soft-Matter Physics,2002,65(6):066109/1- 8.

[8]HOLME P.Edge overload breakdown in evolving networks [J].Physical Review E:Statistical,Nonlinear,and Soft-Matter Physics,2002,66(3):036119/1- 7.

[9]CRUCITTI P,LATORA V,MARCHIORI M.Model for cascading failures in complex networks [J].Physical Review E:Statistical,Nonlinear,and Soft-Matter Physics,2004,69(4):045104/1- 4.[10]王建伟,荣莉莉.基于负荷局域择优重新分配原则的复杂网络上的相继故障 [J].物理学报,2009,58(6):3714- 3721.

WANG Jian-wei,RONG Li-li.Cascading failures on complex networks based on the local preferential redistribution rule of the load [J].Acta Physica Sinica,2009,58(6):3714- 3721.

[11]李涛,裴文江,王少平.无标度复杂网络负载传输优化策略 [J].物理学报,2009,58(9):5903- 5910.

LI Tao,PEI Wen-jiang,WANG Shao-ping.Optimal tra-ffic routing strategy on scale-free complex networks [J].Acta Physica Sinica,2009,58(9):5903- 5910.

[12]段东立,战仁军.基于相继故障信息的网络节点重要度演化机理分析 [J].物理学报,2014,63(6):068902/1- 9.

DUAN Dong-li,ZHAN Ren-jun.Evolution mechanism of node importance based on the information about casca-

ding failures in complex networks [J].Acta Physica Si-nica,2014,63(6):068902/1- 9.

[13]ASZTALOS A,SREENIVASAN S,SZYMANSKI B K,et al.Distributed flow optimization and cascading effects in weighted complex networks [J].European Physical Journal B,2012,85(8):288/1- 10.

[14]MOTTER A E.Cascade control and defense in complex networks [J].Physical Review Letters,2004,93(9):098701/1- 4.

[15]ASZTALOS A,SREENIVASAN S,SZYMANSKI B K,et al.Cascading failures in spatially-embedded random networks [J].Plos One,2014,9(1):e84563/1- 13.

[16]CUPAC V,LIZIER J T,PROKOPENKO M.Comparing dynamics of cascading failures between network-centric and power flow models [J].International Journal of Electrical Power & Energy Systems,2013,49:369- 379.

[17]FANG Y P,PEDRONI N,ZIO E.Comparing network-centric and power flow models for the optimal allocation of link capacities in a cascade-resilient power transmission network [J].IEEE Systems Journal,2014,PP(99):1- 12.[18]LATORA V,MARCHIORI M.Efficient behavior of small-world networks [J].Physical Review Letters,2001,87(19):198701/1- 5.[19]何大韧,刘宗华,汪秉宏.复杂系统与复杂网络 [M].北京:高等教育出版社,2009:143- 153.

收稿日期:2015- 08- 04

*基金项目:国家自然科学基金资助项目(71302153);中国博士后科学基金特别资助项目(2014T70838);广东省自然科学基金资助项目(2014A030313608)

Foundation items: Supported by the National Natural Science Foundation of China(71302153),the Chinese Postdoctoral Science Foundation Funded Project(2014T70838)and the Natural Science Foundation of Guangdong Province(2014A030313608)

作者简介:李从东(1962-),男,教授,博士生导师,主要从事应急管理、系统集成与工业工程研究.E-mail:licd@jnu.edu.cn †通信作者: 邓原(1976-),女,博士生,主要从事复杂网络与系统工程研究.E-mail:dengyuan9966@sina.com

文章编号:1000- 565X(2016)05- 0022- 07

中图分类号：TP 273

doi：10.3969/j.issn.1000-565X.2016.05.004

Dynamic Information-Based Load Reallocation Strategy for Cascading Failure Networks

LICong-dongDENGYuanYUANZhi-fengWANGYu

(Management School,Jinan University,Guangzhou 510632,Guangdong,China)

Abstract:In order to implement load reallocation in cascading failure networks,a dynamic reallocation strategy combining both local and dynamic network information is proposed. In this strategy,the weight is computed according to the degree and real-time processing ability of a node,and is used to reallocate load in turn.At the same time,according to a certain proportion,some failure nodes are selected to suspend their function and their load reallocation processes stop accordingly.Simulated results in BA scale-free network,WS small-world network and ER random network show that,under certain parameter conditions,the proposed dynamic reallocation strategy is superior to betweenness distribution strategy and degree distribution strategy because it is more effective in alleviating cascading failure by reducing the overall network load rate and optimizing network's real-time streaming distribution. Key words: cascading failure;Motter and Lai model;dynamic reallocation strategy;complex networks