基于压缩循环谱的mW复合序列参数估计*

郭黎利　刘湘蒲　付江志　李清伟

(哈尔滨工程大学 信息与通信工程学院, 黑龙江 哈尔滨 150001)



基于压缩循环谱的mW复合序列参数估计*

郭黎利刘湘蒲付江志李清伟

(哈尔滨工程大学 信息与通信工程学院, 黑龙江 哈尔滨 150001)

摘要:针对mW(m-Walsh)复合序列扩频信号的参数估计问题,根据循环谱理论推导了mW复合序列扩频信号的循环谱表达式,并结合Walsh序列的频谱特征分析了mW复合序列扩频信号的循环谱特征,提出了基于循环谱的参数估计算法.针对mW复合序列循环谱的获取所需采样率较高的问题,引入压缩循环谱技术,通过信号的压缩采样值来重构循环谱.实验结果表明,利用压缩采样理论能有效地重构出信号循环谱,并实现对Walsh序列序号、m序列码片速率和载频等参数的有效估计.

关键词：mW复合序列;循环谱;压缩采样;参数估计

作为直接序列扩频通信中的一种复合扩频序列,mW(m-Walsh)复合序列同时具有直扩和跳频(DS-FH)的特性.在该序列的复合过程中,通过改变m、Walsh序列的长度和所选Walsh序列的序号可以控制复合序列能量主瓣在频域的位置和宽度.利用该特性，mW复合序列在通信对抗中可用于规避窄带干扰和部分频带干扰，在移动通信中可用于解决远近效应问题[1].利用扩频信号所具有的低功率谱密度及mW复合序列的频域特征可控特性,还可以将mW复合序列作为认知无线电(CR)通信中直扩认知用户的备选序列,使其发射信号频谱在授权用户工作频段内凹陷,从而实现认知用户的频谱接入[2].

目前,对mW复合序列的研究主要集中在序列生成原理、序列特性分析及序列干扰抑制能力等方面,而对其参数估计方法的研究鲜见报道.mW复合序列属于扩频序列,目前对扩频信号的参数估计方法主要有能量检测法[3]、平方倍频法[4]、自相关法[5]、二次功率谱法[6]和循环谱法[7]等.其中能量检测法在低信噪比下的性能较差,平方倍频法仅能估计载频,自相关法和二次功率谱法可有效估计伪码周期,但不能同时估计载频和码片速率.循环谱法利用扩频信号的循环平稳特性[8],能在低信噪比下估计载频、码片速率等参数信息,但mW复合序列长度一般较长,经其扩频后的发送信号带宽较宽,因此在获取循环谱时,对系统的采样率要求较高.

文中采用循环谱法对mW复合序列扩频信号进行参数估计,推导了其循环谱表达式,分析了循环谱切面特征,并给出了参数估计算法.针对其循环谱获取所需采样率较高的问题,通过挖掘其循环谱所具有的稀疏性,将压缩循环谱技术引入到循环谱的获取中,以降低采样开销.在仿真实验中通过压缩采样值来恢复信号循环谱,并对其峰值进行检测,以实现对mW复合序列中Walsh序列序号、m序列码片速率和载频等参数的估计.

1mW复合序列及其特征

mW复合序列扩频信号x(t)可表示为

(1)

式中:f0为载频;s(t)为mW复合序列,

(2)

g(t)为门函数;m序列的长度为lm、码片mi的宽度为Tm,Walsh序列的长度为lW、码片Wj的宽度为TW,则对应的码片速率分别为fm=1/Tm和fW=1/TW.1.1Walsh序列的频谱特征

Walsh序列目前还没有统一的频谱表达式,且不同长度的Walsh序列具有不同的频谱特征.文中以4阶Hadamard矩阵形成的长度为4的Walsh序列为例,计算其频谱,该频谱计算方法同样适用于其他长度的Walsh序列.

4阶Hadamard矩阵与其生成的Walsh序列的对应关系可表示为

(3)

式中,W(k)表示序号为k的Walsh序列,W(0)为直流信号,不对其进行分析.

定义Π(t)是幅度为1且持续时间为1 s的矩形脉冲信号,则W(1)可写为

(4)

对其求傅里叶变换可得W(1)的频谱为

(5)

类似地,可得到W(2)和W(3)的频谱分别为

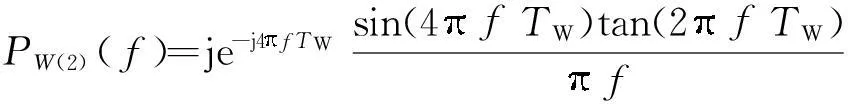
(6)

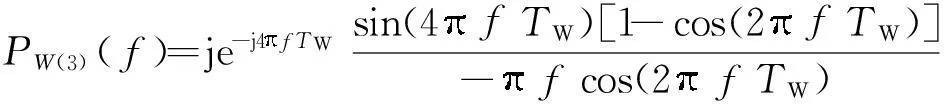
(7)

Walsh序列的序号k与其频谱峰值频率fc具有明确的对应关系[9],如表1所示.

从W(2)到W(lW-1)的Walsh序列对应了(lW-2)/2种不同的fc,其中序号

(8)

的两个序列具有相同的fc.

序号从2p到2p-1-1的Walsh序列的fc与系数γ有关,文献[9]给出了γ的具体求解方法,在此不再赘述.以式(3)所示的Walsh序列为例,W(1)的fc=fW/2,W(2)和W(3)具有相同的fc=fW/4,此时,p=1,q=0,γ=1.

表1　Walsh序列的k与fc的关系

1.2mW复合序列循环谱特征

mW复合序列s(t)的表达式与脉冲幅度调制(PAM)信号及二进制偏移载波(BOC)信号类似,根据PAM信号[7]和BOC信号[10]循环谱的推导过程,可得到s(t)的循环谱表达式:

(9)

式中,α为循环频率,f为频率,P(f)为Walsh序列频谱,P*(f)为P(f)的共轭,

(10)

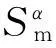
(11)

其中l取整数.

x(t)的循环谱与基带信号s(t)循环谱的关系可表示为[11]

(12)

将s(t)的循环谱表达式(11)代入式(12),并取频率f=0,可得mW复合序列扩频信号x(t)的循环谱切面(f=0)表达式为

(13)

将Walsh序列频谱表达式代入式(13),可得各mW复合序列扩频信号的循环谱切面表达式.

当α=l/Tm时,

(14)

当α=±2f0+l/Tm时,

(15)

式中，sinc(·)表示辛格函数

由以上表达式可得到mW复合序列扩频信号的循环谱切面峰值位置,如表2所示.

表2mW复合序列扩频信号的循环谱切面峰值位置

Table 2Peak position of cyclic spectrum section of mW composite sequence spread spectrum signal

复合序列主峰位置次峰位置mW(1)-2f0±fW,2f0±fW-2f0±fW∓fm,2f0±fW∓fmmW(2)-2f0±fW2,2f0±fW2-2f0±fW2∓fm,2f0±fW2∓fmmW(3)-2f0±fW2,2f0±fW2-2f0±fW2±fm,2f0±fW2±fm

可以看出,mW复合序列经调制后,在f=0的循环谱切面上出现4个主峰和4个次峰,且主峰和次峰均关于α=0对称分布,这些峰值位置包含了载频、m序列和Walsh序列的码片速率等信息.

通过频域平滑循环周期图法得到的x(t)的循环谱切面如图1所示(图中仅给出了正循环频率轴,负循环频率轴与其对称),所选取的数据长度为8 192,对坐标进行了归一化处理.可以看出,图1中所示的峰值位置与表2结果一致.

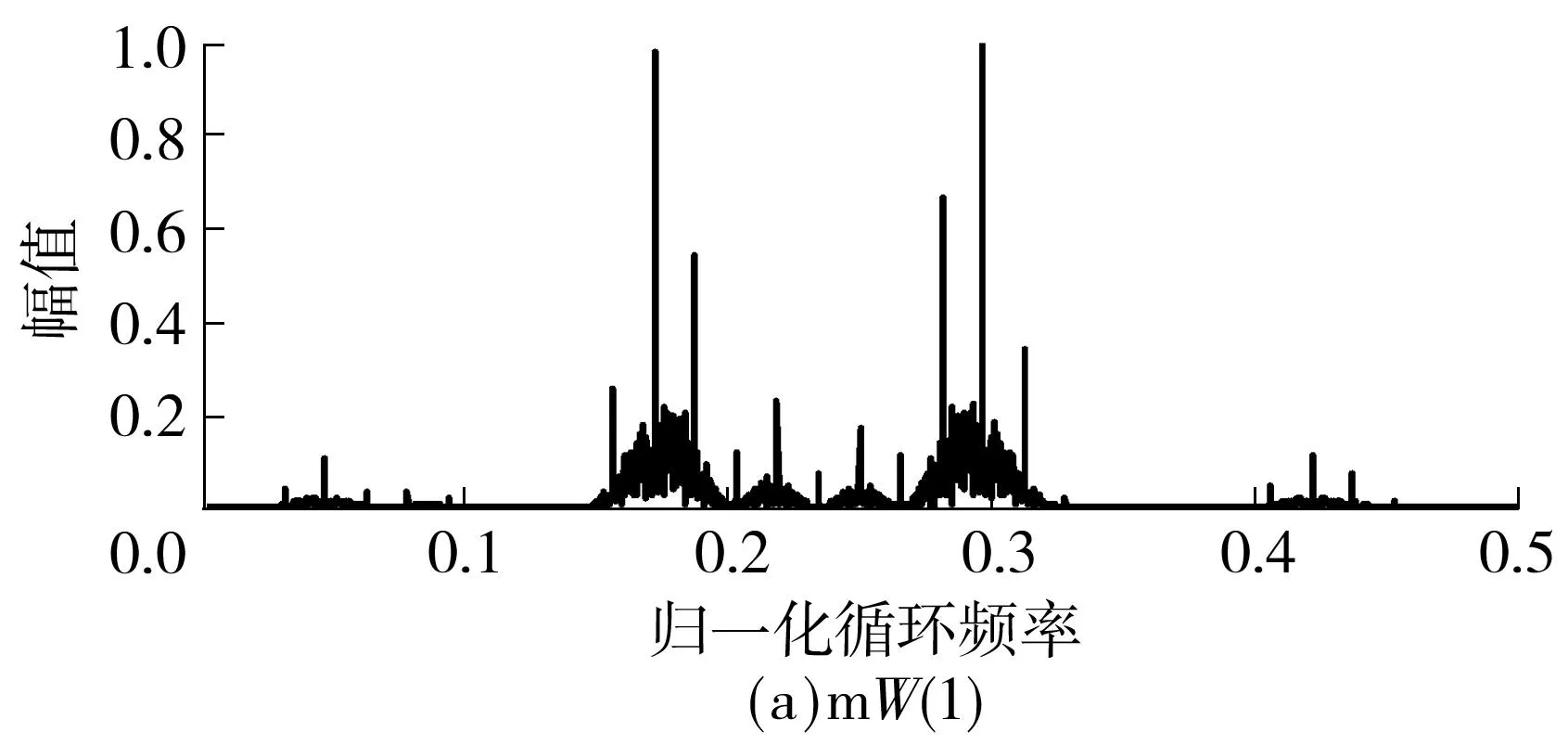
图1　mW复合序列扩频信号的循环谱切面图

Fig.1Cyclic spectrum section of mW composite sequence spread spectrum signal

2基于循环谱的参数估计算法

根据表1、表2和图1所示的结果,在正循环频率轴上对循环谱切面进行分析可知,mW复合序列扩频信号循环谱切面具有如下特征:

(1)对于不同的复合序列,两主峰的中间位置为两倍载频2f0;

(2)mW(1)的主峰间距为2fW,mW(2)和mW(3)的主峰间距为fW,且所有复合序列的主峰间距均为4fc,根据该特征可估计出频谱峰值频率fc,并由此区分出mW(1);

(3)所有的次峰值均出现在距主峰fm的位置,由此可估计出m序列的码片速率;

(4)mW(1)和mW(2)的两次峰位于两主峰内侧,而mW(3)的两次峰位于两主峰外侧,利用该特征并结合特征(2),可区分mW(2)和mW(3).

根据以上分析,文中提出的参数估计算法的具体步骤如下:

(4)比较p1和p2位置处两主峰峰值的大小,将峰值较大的主峰位置记为p5,并将其邻域内的次峰记为p6.

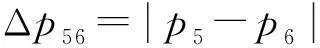
3压缩循环谱

由mW复合序列的循环谱结构可知,在(α,f)平面上,其循环谱具有极强的稀疏性.因此,可将压缩采样(CS)[12]理论引入到mW复合序列循环谱的获取中,从而降低系统采样率[13- 14].

设定x(t)的奈奎斯特采样数为NT,采样值用向量xT表示.为了获得更好的循环谱估计效果,将NT个采样值均分为L段,每段的采样值数为N,用xl∈RN表示,NT=NL.

对信号xl进行压缩采样

zl=Axl

(16)

式中,zl∈Rm为压缩采样值,A∈Rm×N为压缩采样矩阵.则压缩率κ=m/N<1.

定义信号xl的协方差矩阵为Rx,Rx∈RN×N，

(17)

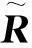
rx=[rx(0,0),rx(1,0),…，rx(N-1,0)，rx(0,1),

rx(1,1),…,rx(N-2,1),…，rx(0,N-1)]T

(18)

(19)

vec(Rx)=PNrx

(20)

(21)

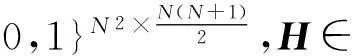
同理,对于压缩采样值zl,可以类似地定义Rz和rz,并得到rz与Rz的对应关系:

rz=Qmvec(Rz)

(22)

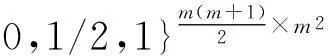
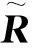
(23)

定义sx=vec(Sx),结合式(21)和(23),并由vec(ABC)=(CT⊗A)vec(B)[15]可得

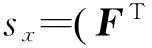
(24)

式中,⊗为矩阵的克罗内克积,I为单位矩阵.

由于zl=Axl,故Rz与Rx具有如下关系:

Rz=ARxAT

(25)

故由式(20)、(22)、(25)可得

rz=Qm(A⊗A)PNrx

(26)

rz=Ψrx

(27)

(28)

(29)

由于sx具有稀疏性,故由压缩感知理论可知,sx可通过l1范数最小化来重构:

(30)

(31)

4仿真实验与结果分析

在所有的仿真实验中,选取长度为127的m序列与长度为4的Walsh序列复合形成mW复合序列,设定m序列码片速率fm=25 MHz,Walsh序列码片速率fW=100 MHz,载频f0=187.5 MHz,奈奎斯特采样率fs=800 MHz.

在通过压缩采样值重构循环谱的过程中,将奈奎斯特采样值均分为L=400段,每段数据长度N=128.压缩率κ=m/N,压缩采样矩阵A为高斯随机矩阵.为了降低噪声的影响,用于参数估计的循环谱是10次重构得到的循环谱的平均值.

4.1通过压缩采样值重构循环谱

在无噪环境下通过压缩采样值重构的循环谱切面图如图2所示,压缩率κ=0.75.根据表1可知:mW(1)的主峰位置分别为275和475 MHz,次峰位置分别为300和450 MHz;mW(2)的主峰位置分别为325和425 MHz,次峰位置分别为350和400 MHz;mW(3)的主峰位置分别为325和425 MHz,次峰位置分别为300和450 MHz.可以看出,图2中所有的峰值位置均与上述结果一致,由此验证了通过压缩采样值重构mW复合序列扩频信号循环谱的可行性.

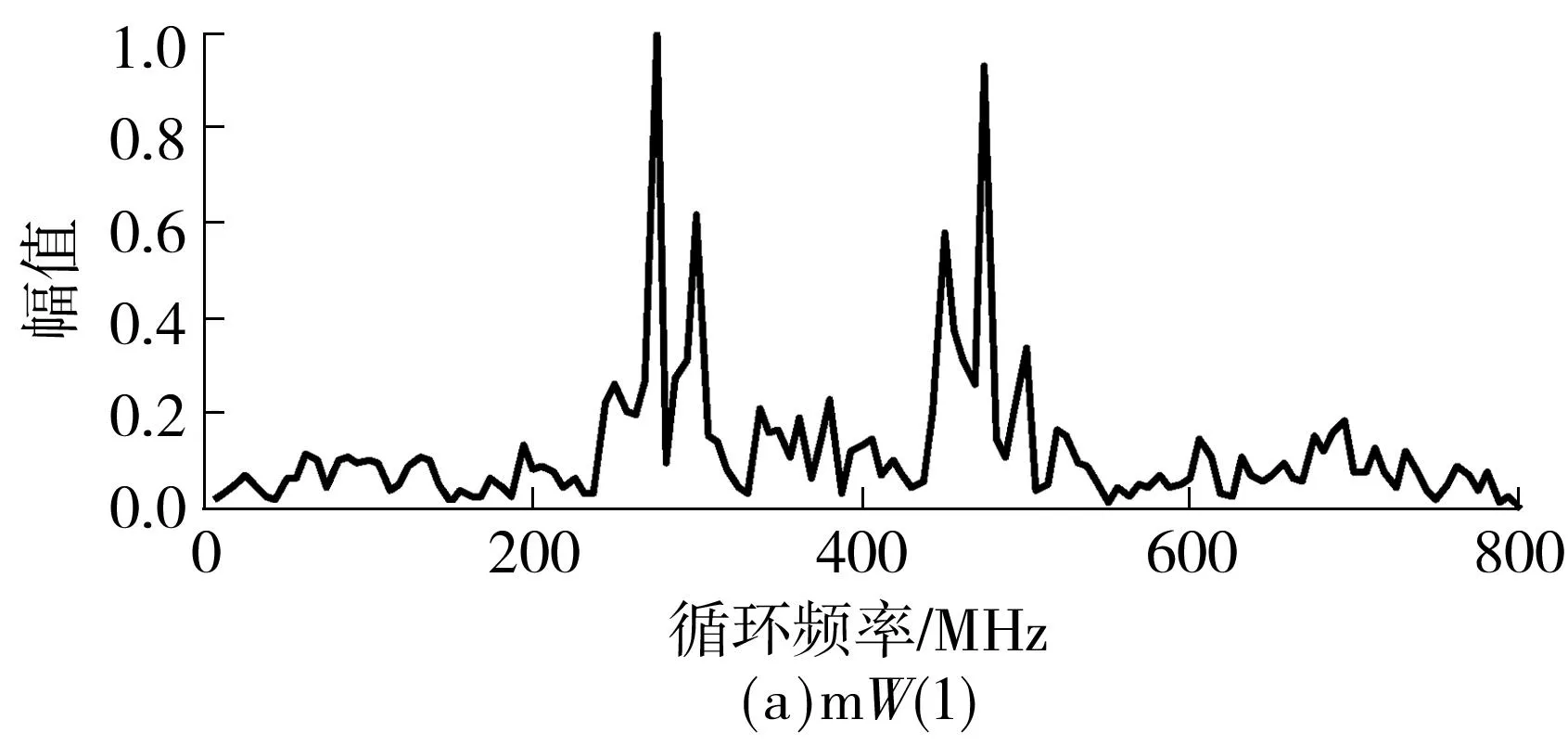
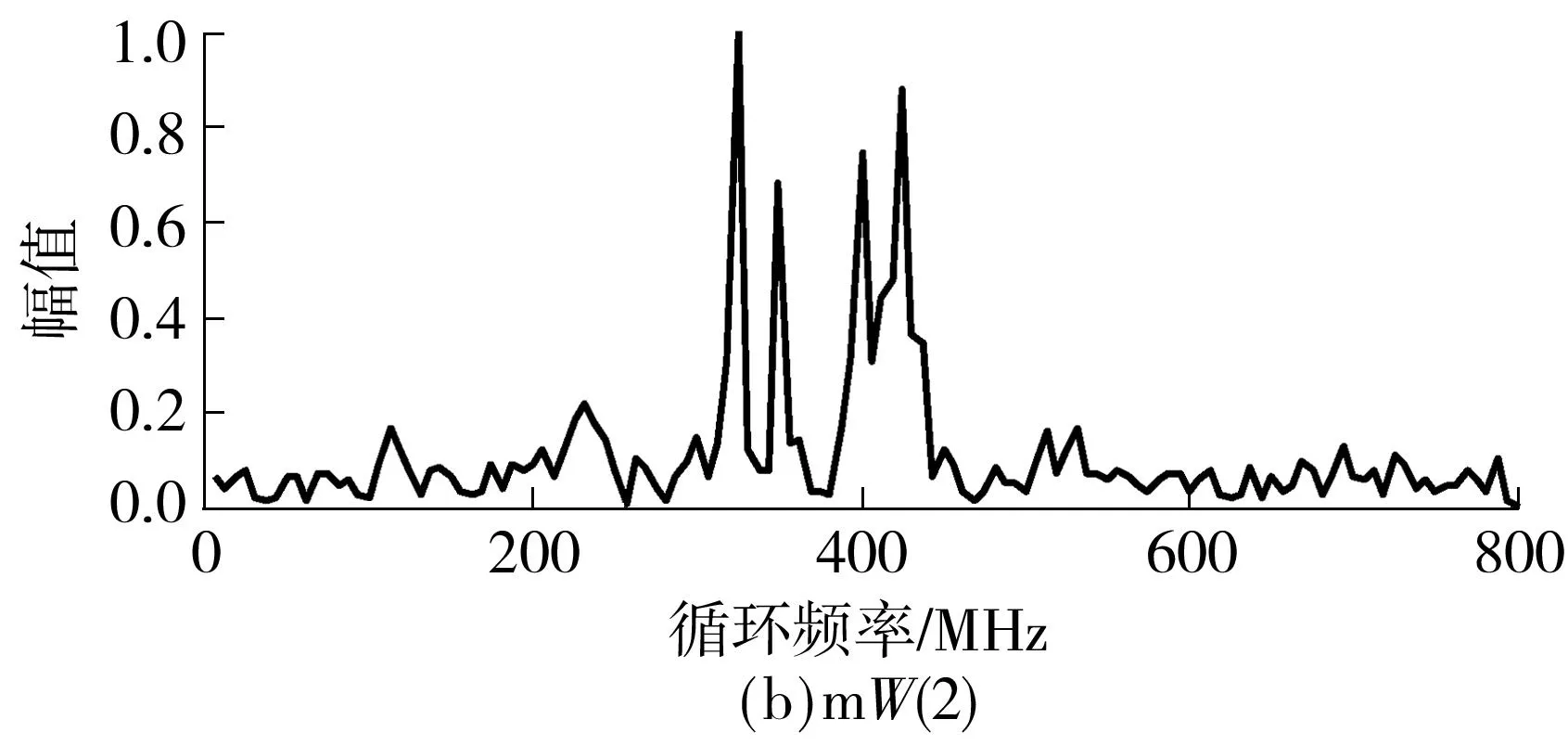
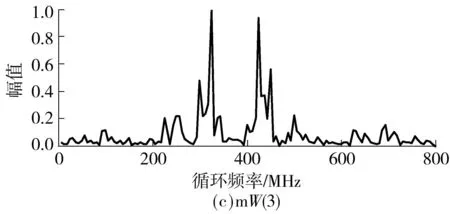
图2　通过压缩采样值重构的循环谱切面图

4.2参数估计性能

在高斯白噪声环境下仿真分析mW复合序列扩频信号各参数的估计性能.所有的仿真实验均进行500次,每次随机选取mW(1)-mW(3)中的一条复合序列进行参数估计,并得到估计性能的衡量标准.其中,载频和m序列码片速率估计的衡量标准为归一化均方误差βNMSE,Walsh序列序号估计的衡量标准为序号估计正确率η,仿真结果如图3、4所示.压缩率κ分别选取0.65、0.75和0.85,则对应的系统采样率fs从800 MHz分别降低为520、600和680 MHz.为便于比较,文中还给出了κ=1时的参数估计结果,当κ=1时,A为单位矩阵，即A=I∈RN×N，表示没有降低系统采样率.

从图3(a)可知:随着信噪比的增加,估计的βNMSE逐渐减小;当κ取0.75和0.85时,βNMSE分别在信噪比为-9和-12 dB时开始收敛,且βNMSE值与κ=1.00时的βNMSE值相当;当κ=0.65时,βNMSE在信噪比为-5 dB时开始收敛,但其βNMSE值明显大于κ=1.00时的βNMSE值;对于不同的压缩率κ,即使βNMSE开始收敛,载频估计的结果仍然具有很小的估计误差,这是由于载频的估计值由两主峰的位置获得,而在噪声环境中,通过压缩采样值重构的循环谱可能会出现某一次峰峰值大于相邻主峰峰值的情况,从而造成载频的估计误差.

图3　载频估计和m序列码片速率估计的归一化均方误差

Fig.3Normalized mean square errors of carrier frequency and m sequence chip rate estimation

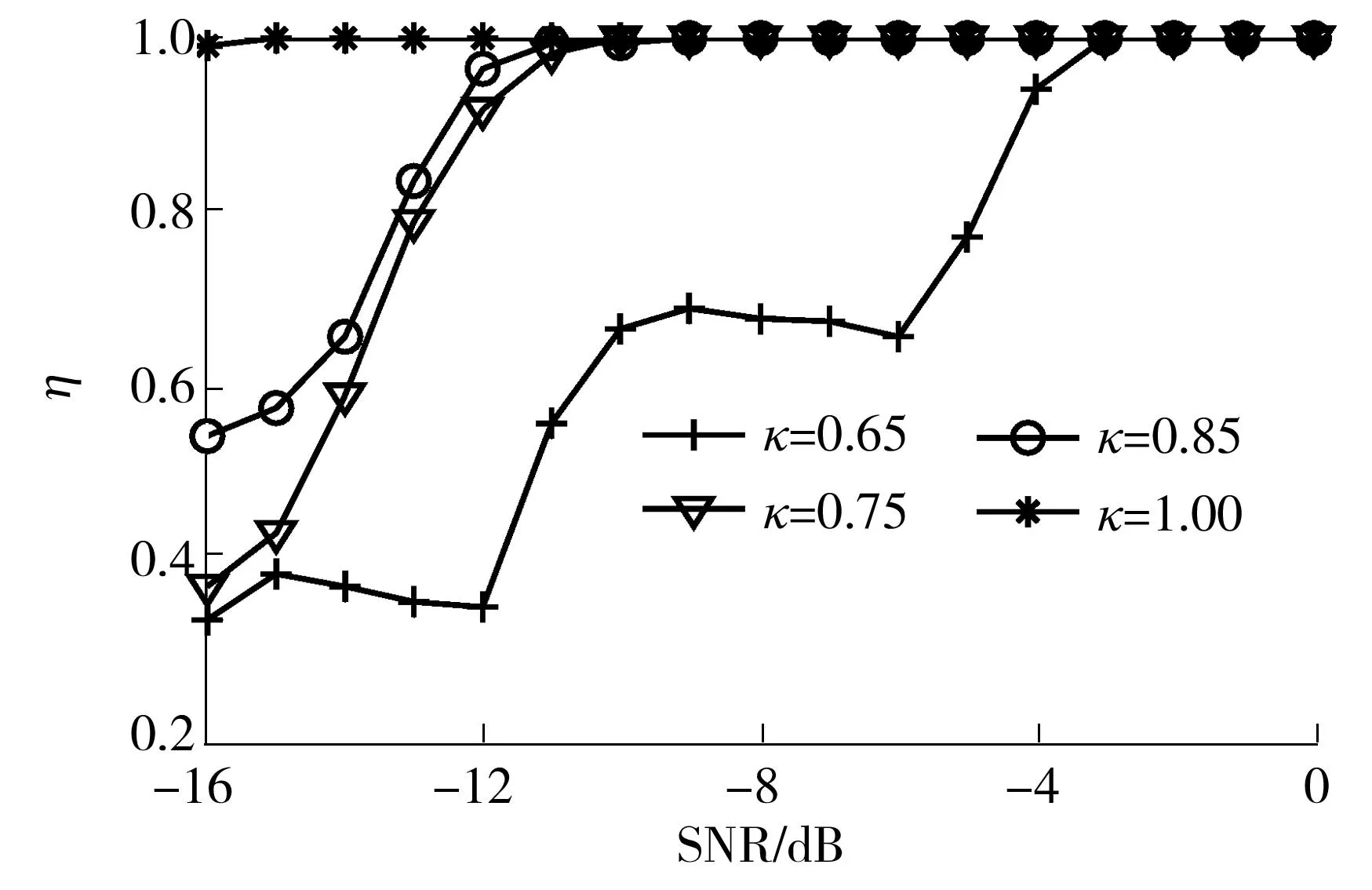
图4　Walsh序列序号估计的正确率

从图3(b)可知:当κ取0.75和0.85时,βNMSE分别在信噪比为-5 和-9 dB时开始收敛,且βNMSE值与κ=1.00时的βNMSE值相当;当κ=0.65时,即使信噪比增加,也不能很好地进行m序列码片速率的估计,这是由于压缩率较低时,不能很好地重构循环谱切面的次峰值,从而造成较大的码片速率估计误差.比较图3可以看出,载频估计的性能优于m序列码片速率估计的性能,这是由于载频由两主峰位置获得,而m序列码片速率由主峰及其相邻次峰之间的间距获得,在峰值位置的检测过程中,次峰比主峰更易受噪声的影响.

从图4可以看出:当κ取0.75和0.85时,在信噪比大于-12 dB后η>0.9,且在信噪比大于-9 dB后序号估计的正确率与κ=1.00时相当;当κ=0.65时,在信噪比大于-3 dB后序号估计的正确率与κ=1.00时相当.

5结论

利用扩频信号所具有的循环平稳特征,以及基于循环谱法进行参数估计所具备的优越性,文中采用循环谱来实现mW复合序列扩频信号的参数估计,推导和分析了mW复合序列的循环谱特征,给出了可用于估计Walsh序列序号、m序列码片速率和载频的参数估计算法,并分析比较了其参数估计性能.针对其循环谱获取所需采样率较高的问题,文中通过压缩采样值来重构信号循环谱,有效降低了系统采样开销.仿真实验结果验证了该参数估计算法的可行性和有效性.

参考文献：

[1]郭黎利.具有DS/FH频谱特性的复合序列扩频通信方式 [J].哈尔滨工程大学学报,1998,19(4):24- 30.

GUO Li-li.Communication mode of composite sequence spread spectrum with DS/FH spectrum feature [J].Journal of Harbin Engineering University,1998,19(4):24- 30.[2]郭黎利,刘湘蒲,付江志,等.基于块编码的功率谱可控复合序列 [J].哈尔滨工程大学学报,2015,36(2):248- 251.

GUO Li-li,LIU Xiang-pu,FU Jiang-zhi,et al.Controllable composite sequence of power spectral density based on the block coded signal [J].Journal of Harbin Engineering University,2015,36(2):248- 251.

[3]URKOWITZ H.Energy detection of unknown deterministic signals [J].Proceedings of IEEE,1967,55(4):523- 531.

[4]HILL D A,BODIE J B.Carrier detection of PSK signals [J].IEEE Transactions on Communications,2001,49(3):487- 496.

[5]BUREL G,BOUDER C,BERDER O.Detection of direct sequence spread spectrum transmissions without prior knowledge [C]∥Proceedings of 2001 IEEE GLOBECOM.San Antonio:IEEE,2001:236- 239.

[6]张天骐,周正中,邝育军,等.低信噪比长伪码直扩信号伪码周期估计方法 [J].系统工程与电子技术,2007,29(1):12- 16.

ZHANG Tian-qi,ZHOU Zheng-zhong,KUANG Yu-jun,et al.New method for periodic estimation of the PN sequence in the lower SNR long code DS-SS signals [J].Systems Engineering and Electronics,2007,29(1):12- 16.

[7]GARDNER W A.Spectral correlation of modulated signals:Part II-digital modulation [J].IEEE Transactions on Communication,1987,35(6):595- 601.[8]VLOK J D,OLIVIER J C.Blind sequence-length estimation of low-SNR cyclostationary sequences [J].IET Communications,2014,8(9):1578- 1588.

[9]郭黎利,付江志,崔永生,等.采用m-W复合序列的直扩系统规避窄带干扰的研究 [J].哈尔滨工程大学学报,2010,31(5):646- 651.

GUO Li-li,FU Jiang-zhi,CUI Yong-sheng,et al.Using m-Walsh composite sequences to reduce narrow-band interference in direct sequence spread spectrum systems [J].Journal of Harbin Engineering University,2010,31(5):646- 651.

[10]张天骐,何丹娜,陈适,等.基于谱相关的BOC调制信号参数估计 [J].华中科技大学学报(自然科学版),2013,41(9):11- 16.

ZHANG Tian-qi,HE Dan-na,CHEN Shi,et al.Spectral correlation-based parameter estimation of BOC modulation signal [J].Journal of Huazhong University of Science and Technology(Natural Science Edition),2013,41(9):11- 16.

[11]WANG Hong.Spectral correlation function of basic analog and digital modulated signals [C]∥Proceedings of IEEE TENCON 2013.Xi’an:IEEE,2013:1- 5.

[12]DONOHO D L.Compressed sensing [J].IEEE Transactions on Information Theory,2006,52(4):1289- 1306.

[13]TIAN Zhi.Cyclic feature based wideband spectrum sen-sing using compressive sampling [C]∥Proceedings of 2011 IEEE International Conference on Communications.Kyoto:IEEE,2011:1- 5.

[14]COHEN D,ELDAR Y C.Cyclic spectrum reconstruction from sub-Nyquist samples [C]∥Proceedings of 2014 IEEE Global Communications Conference.Austin:IEEE,2014:3132- 3137.

[15]TIAN Zhi,TAFESSE Y,SADLER B M.Cyclic feature detection with sub-nyquist sampling for wideband spectrum sensing [J].IEEE Journal of Selected Topics in Signal Processing,2012,6(1):58- 69.

[16]REBEIZ E,JAIN V,CABRIC D.Cyclostationary-based low complexity wideband spectrum sensing using compressive sensing [C]∥Proceedings of 2012 IEEE International Conference on Communications.Ottawa:IEEE,2012:1619- 1623.

收稿日期:2015- 04- 30

*基金项目:国家自然科学基金资助项目(61271263)

Foundation item:Supported by the National Natural Science Foundation of China(61271263)

作者简介:郭黎利(1955-),男,教授,博士生导师,主要从事扩频通信技术研究.E-mail:guolili@hrbeu.edu.cn

文章编号:1000- 565X(2016)05- 0029- 07

中图分类号：TN 914.42

doi：10.3969/j.issn.1000-565X.2016.05.005

Parameter Estimaton of mW Composite Sequence Based on Compressive Cyclic Spectrum

GUOLi-liLIUXiang-puFUJiang-zhiLIQing-wei

(College of Information and Communication Engineering,Harbin Engineering University,Harbin 150001,Heilongjiang,China)

Abstract:In order to implement the parameter estimation of mW (m-Walsh) composite-sequence spread spectrum signals,the corresponding cyclic spectrum is derived according to the theory of cyclic spectrum,and the feature of cyclic spectrum is analyzed on the basis of spectrum characteristics of Walsh sequence,with a parameter estimation algorithm on the basis of cyclic spectrum being also presented.Moreover,a compressive cyclic spectrum is introduced to meet the high-rate sampling for the calculation of cyclic spectrum.Thus,the cyclic spectrum can be reconstructed from compressive samples.Simulated results indicate that the introduction of compressive sampling helps effectively reconstruct the cyclic spectrum and estimate the sequence number of Walsh sequence,the chip rate of m sequence as well as the carrier frequency.

Key words:mW composite sequence;cyclic spectrum;compressive sampling;parameter estimation