采用气动措施对拉索表面压力分布试验研究

宫赛　唐鹏（南阳理工学院，河南　南阳　473004）



采用气动措施对拉索表面压力分布试验研究

宫赛唐鹏
（南阳理工学院，河南南阳473004）

摘要：基于斜拉桥拉索风雨激振理论，制作了用于测压试验的拉索模型，分析了不同气动措施的三维拉索表面风压系数分布以及不同表面状态的拉索气动力系数的变化规律，为斜拉索气动抑振措施的研究提供了理论依据。

关键词：斜拉桥，拉索，风雨激振，气动措施，风压系数

0　引言

随着世界经济的发展，斜拉桥作为具有大跨度桥梁能力之一，跨度越来越大，但是在特殊条件下，例如在风雨共同作用下，作为斜拉桥主要受力部件之一——拉索会产生剧烈的振动。国内外许多学者对拉索风雨激振的机理及抑振措施研究往往是在二维拉索模型上获得试验结果［1］。而从三维空间关系出发的研究较少，虽然可以通过对拉索缠绕螺旋线降低拉索的风雨条件下的振动，但拉索的表面被螺旋线缠绕而发生改变，将会对拉索的气动性能产生一定的影响。因此，有必要从三维拉索模型的风洞测压试验出发，对风阻系数与气动抑振措施螺旋线参数的关系进行研究［2，3］。

1　试验模型、工况

试验模型及参数如下：拉索节段模型采用轴向长64 cm、直径200 mm、壁厚5 mm的塑料管材。拉索一端固定在可以自由水平转动的β机构上，另一端自由。拉索存在倾角和风向角［5］，是其在风雨作用下产生振动的必要条件，但是在这种作用下，倾角与风向角对拉索的振动相比，墙角可以忽略不计［6］，在进行试验时，固定拉索倾角在35°，使风向角在0°～90°之间变化。模型倾角α和风向角β见图1。

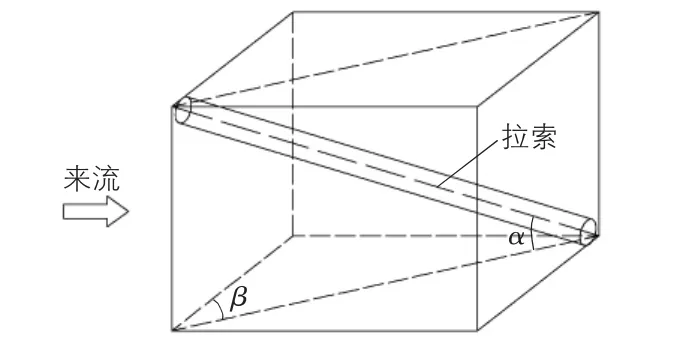
图1　斜拉索倾角α和风向角β示意图

为研究风荷载作用在拉索上的分布特性，在φ200斜拉索每个断面设置31个测压孔，有4个断面，共124个测压孔，其弧向间距为20 mm（见图2）。测压孔的每个断面距模型自由端面依次为0 cm，15.5 cm，21 cm，26.5 cm；拉索表面缠绕螺旋线是现有抑制风雨激振的气动的一种常用措施［7］，本试验采用圆形PE胶管粘贴在拉索表面的双螺旋缠绕。螺旋线线径分别为2 mm，4 mm，6 mm，螺距为400 mm，500 mm，600 mm（见图3）；为研究水线对拉索的影响，在试验中计入模拟水线，使其水线位置在10°～80°之间变化，步长为10°，水线断面设计成高1 mm宽12 mm的矩形截面。模型安装见图4。

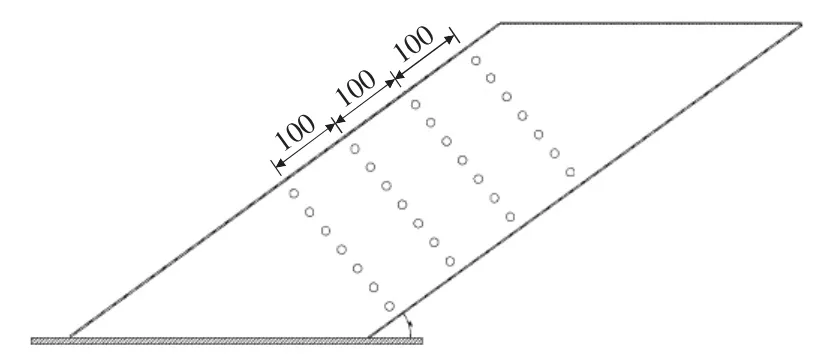
图2　拉索测压孔的布置（单位：mm）

图3　带螺旋线和水线的拉索模型

图4　模型安装图

由图5可以看出，在风向角、风速不同的条件下，各个断面上的平均风压分布趋势基本一致。三围流对模型的影响可以通过采用距离模型节段自由端1 cm的端板而较好的消除。与其他断面的平均风压分布系数变化比较，第一个测压断面变化剧烈，而二、三断面变化较居中。

2　风压、动力系数定义

其中，风压值以风压受力面受压为正，反则为负。ρ为空气密度；U0为风速；p - p0为测点的风压值与来流静压之差。通过Matlab和Origin软件分析对原始数据进行处理。

通过各测压点的风压系数式（2）和式（3）计算得到拉索气动力系数Cx和Cy：

其中，Fx，Fy分别为X和Y方向的气动力；Cpi为第i个测点的风压系数；R为拉索模型半径；Δφi为第i与i + 1个测点间的交角；φi为第i个测压点的位置角（见图6，图7）。

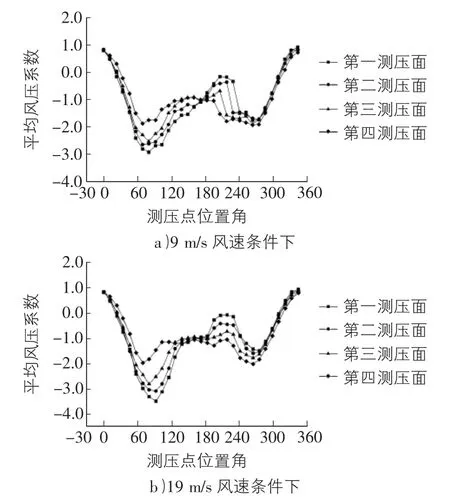
图5　β=30°各测压断面的平均风压分布

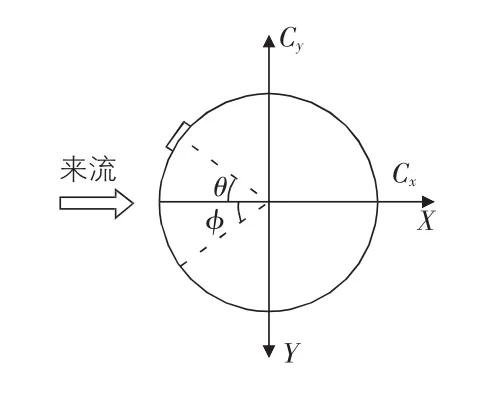
图6　测点位置角φ与水线位置角θ

图7　φ200 mm拉索模型测压点布置图

3　气动力系数分析

针对拉索在不同表面状态下的风压系数，采用光面拉索，缠绕螺旋线，同时有水线、缠绕螺旋线的模型表面研究。

3.1光面拉索的静气动力系数分析

φ200 mm光面拉索的Cx和Cy示意图见图8。

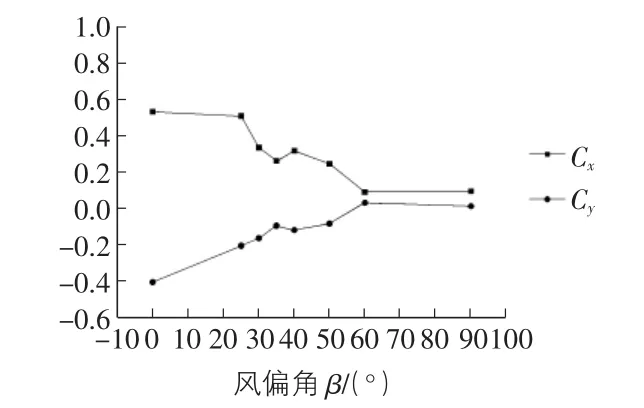
图8　φ200 mm光面拉索的Cx和Cy

在风向角变化的条件下，模型的静气动力系数也随之产生变化，当风向角在25°～40°之间变化时，系数的这种变化就变得更为强烈，所以风向角的确定对拉索模型表面的风压系数以及气动力系数有较大的影响。

3.2拉索缠绕螺旋线的气动力系数分析

研究螺旋线气动措施的主要目的是确定拉索风阻系数小的螺旋线参数［8］，图9，图10是φ200拉索对气动系数在采用不同螺旋线参数下的影响。其中K1，K2表示螺旋参数。

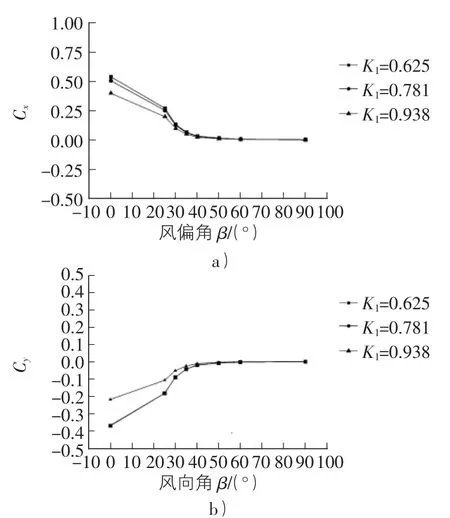
图9　K1不同的拉索气动力系数Cx和Cy

图10　K2不同的拉索气动力系数Cx和Cy

从图9，图10可以看出，当K1值在0.625和0.781范围内时Cx与Cy相当，当K1值在0.938时Cy较小；K2在0.01和0.02范围内时Cx和Cy比较接近，但K2值为0.02时，模型Cx和Cy影响较小［9］。

3.3同时有水线、缠绕螺旋线的拉索静气动力系数分析

拉索表面水线的振动会使其气动力也产生变化［2］。在试验中采用K1值为0.938，K2值为0.03时的参数进行计算（见图11）。

图11　Cx和Cy在同风向角时随水线角度的变化

4　结语

通过试验对斜拉桥拉索模型的表面受缠绕螺旋线、水线以及风向角等参数计入的研究，从而得出其风压以及气动力系数变化规律。风向角的选择，水线的位置的确定，缠绕螺旋线参数，同时有水线、缠绕螺旋线参数的模型气动参数分析发现，在其余参数相同的前提下，从抗风角度出发，螺旋线参数的取值应选择K1较大的值，而K2的选取范围在0.02左右较为合适。

参考文献：

［1］杜晓庆.斜拉桥拉索风雨激振研究［D］.上海：同济大学博士学位论文，2003：12.

［2］杜晓庆，顾明.斜拉索上雨线的气动力特性的试验研究［J］.同济大学学报（自然科学版），2005，33（5）：585-589.

［3］Y.Hikami，N.Shiraish.Rain-wind induced vibration of cables in cable stayed bridges［J］.J.of Wind Engineering and Industrial Aerodynamics，1988（29）：409-418.

［4］顾明，杜晓庆.模拟降雨条件下斜拉索风雨激振及控制的试验研究［J］.土木工程学报，2004，37（7）：101-104.

［5］李文勃.斜拉桥拉索三维风雨激振及静风荷载研究［D］.上海：同济大学博士学位论文，2007.

［6］顾明，杜晓庆.不同风向角下斜拉桥拉索模型测压试验研究［J］.振动与冲击，2005，24（6）：5-20.

［7］顾明，杜晓庆.带人工雨线的斜拉桥拉索模型测压试验研究［J］.空气动力学学报，2005，23（4）：419-424.

［8］Yamaguchi H.Analytical study on growth mechanism of rain vibration of cables［J］.Journal of Wind Engineering and Industrial Aerodynamics，1990（33）：73-80.

［9］陈政清.桥梁风工程［M］.北京：人民交通出版社，2005.

Study on surface pressure distribution test of stayed-cable using aerodynamic measure

Gong Sai Tang Peng
（Nanyang Institute of Technology，Nanyang 473004，China）

Abstract：The theoretical basis of the thesis is oblique stayed bridge rain wind induced vibration of stay cable theory，design and make the cable model for pressure test，analysis in different aerodynamic measures dimensional cable surface wind pressure coefficient distribution and variation law of different surface state of cable aerodynamic coefficients，cable and gas dynamic anti vibration measures the next step of the research provides a theoretical support.

Key words：cable-stayed bridge，cable，wind rain induced vibration，aerodynamic measure，wind pressure coefficient

中图分类号：U448.27

文献标识码：A

文章编号：1009-6825（2016）06-0165-03

收稿日期：2015-12-02

作者简介：宫赛（1986-），女，硕士，讲师；唐鹏（1987-），男，硕士，讲师