Study of formation boundary and dip attribute extraction based on edge detection technology

WANG Yanbo, SUN Jianguoand SONG Chao

CollegeofGeo-ExplorationScienceandTechnology,JilinUniversity,Changchun130026,China



Study of formation boundary and dip attribute extraction based on edge detection technology

WANG Yanbo, SUN Jianguo*and SONG Chao

CollegeofGeo-ExplorationScienceandTechnology,JilinUniversity,Changchun130026,China

Abstract:In the seismic profile interpretation process, as the seismic data are big and the small geological features are difficult to identify, improvement of the efficiency is needed. In this study, structure tensor method in computer image edge detection processing is applied into the 2D seismic profile. Coherent attribute is used to extract formation edge. At the same time, extracting the eigenvalues and eigenvectors to calculate the seismic geometric properties which include dip and apparent dip, automatic identification is achieved. Testing the Gaussian kernel function with synthetic models and comparing the coherent attribute and dip attribute extraction results before and after, the conclusion that Gaussian filter can remove the random noise is obtained.

Key words:edge detection; structure tensor; coherent attribute; dip attribute; Gaussian kernel smooth filter

1Introduction

Edge is the basic feature of the image. Image processing technology is based on the edge detection which is usually the first stage of image processing in machine vision systems, and it is one of the classic researches in machine vision field. The correctness and the reliability of the detecting results will directly affect the understanding of the objective world in machine vision systems (Duanetal., 2005).

Edge detection focuses on image contrast ratio. Detecting contrast ratio is to detect the difference of brightness in different areas. Through the detection of contrast ratio, we can extract the edges of the images, and edges are the areas where vary obviously in brightness. People can identify the edges of objects because of the differences in brightness between target objects and their surroundings. When there is an edge, the first derivative of brightness will get bigger. On the contrary, the first derivative will not response.

In machine vision field, acquiring image edge information is usually the first step to receive the image information in machine vision systems and computer systems. In image segmentation field, many segmentation methods are directly based on the results of edge detection to process target segmentation.

2Theory and method

2.1Summary of structure tensor theory

In vector calculation, the gradient of the scalar field is a vector field. The scalar field gradient at one point represents the change rate direction of the scalar field, and the value of the gradient represents the change rate. As to linear function, gradient is the slope of the function. It represents the level of inclination along a certain direction of a curving surface. In computer image processing, the gradient reflects the structure of the object in the image. So it can be used to extract the geometric features of the objects or to provide a theoretical basis for other computer visua-lization methods. For example, the most important method of circuit pattern recognition is the local edge detection of big gradient values.

In the multivariate differentiable function, directional derivative is the instantaneous change rate of a point along a certain direction. In Fig.1, the directional derivative is the gradient value calculated from the image. The direction of the arrow is the direction of the directional derivative; and the length of the arrow is the value of the directional derivative.

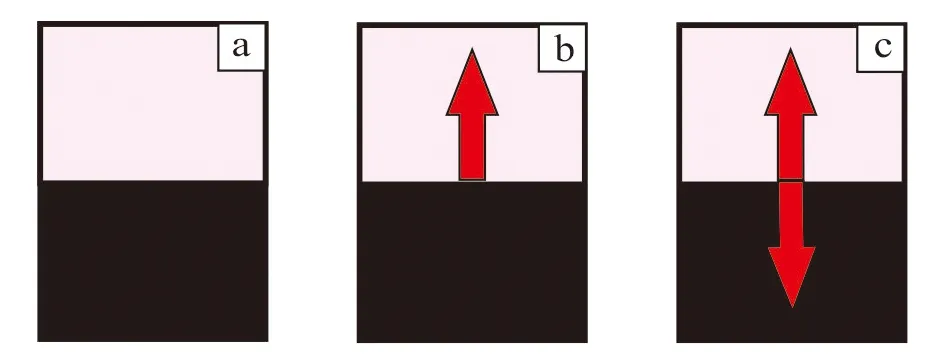
Fig.1　Schematic diagram of directional derivative

The value and the direction of the directional derivative are given as following:

(1)

Where Ixand Iyare the partial derivatives of the image element I along the x axis and y axis, respectively.

The gradient information can also be represented by the structure tensor. The tensor is an array as matrix, the difference is that the tensor is a physical quantity, which is not affected by the change of coordinate system. Tensor can be represented as matrix and its exponent values can be represented by the order of this matrix. For example, a zero-order tensor is a scalar value x; a first-order tensor is a vector v and a second-order tensor is a two-dimensional matrix Mij.

For example, the first-order structure tensor matrix of a two-dimensional data model can be expressed as following:

(2)

Two eigenvalues (λ1,λ2) and two corresponding eigenvectors (e1,e2) are obtained after doing the eigenvalue decomposition with respect to Eq.(2). These two eigenvalues represent the gradient values along the direction of gradient, e1is perpendicular to the edge of the gradient, while e2is parallel to the edge of the gradient. The structure information calculated by eigenvalues can identify the consistency of data (Jähne, 1993; Medionietal., 2000; Deriche, 2002). In the application of gradient structure tensor (GST), Gaussian function can enhance the anti-noise ability in the process of the structure information extraction (Zhangetal., 2007).

2.2Characteristics analysis of image structure tensor

The structure tensor is a kind of matrix data field. A two-dimension image data matrix can be expressed as Ω⊂R2, and its grayscaleIcan be expressed as Ω⊂R. The edge energy and direction can be calculated by the initial structure tensor matrix of each pixel point in the image. This initial structure tensor matrix is constructed by calculating gradient (Färstner & Gülch, 1987), and the gradient of the point I(i,j) is (Yangetal., 2002)：

(3)

The initial structure tensor of this point is

(4)

Due to the Gaussian filter has better de-noising effect, Gaussian filter is widely applied in image processing method. In this paper, the convolution of the initial structure tensor field and Gauss kernel function is realized by smoothing structure tensor:

(5)

Where, Gris the Gaussian kernel function whose standard deviation is r. Because the convolution of the structure tensor and the Gauss kernel function is a linear process, many papers have called the classical structure tensor as the linear structure tensor (Bigünetal., 1991; Broxetal., 2006; Zhengetal., 2008). The linear structure tensor also has half positive defi-nitiveness. The linear structure tensor obtained by this de-noising process can better reflect the information of edge and direction.

At present, linear structure tensor contains more information than gradient does, because we integrate neighbor pixels information during the linear smooth processing. Using eigenvalue decomposition method to Eq. (5), two eigenvalues λ1≥λ2(from big to small) and their corresponding eigenvectors v1⊥v2are obtained.

The method of structural information extraction is given as follows:

(6)

If λ1and λ2are close to zero, there is no gradient energy or structure can be detected; if λ1and λ2are both bigger than zero, there is a deformation caused by bending and pleiotropia; if λ1is the bigger and λ2is close to zero, it represents a linear structure. The area which has big values is the edge of formation however it is represented by condition number or coherent attribute. In this paper, the formation edge is calculated by coherent attribute.

2) The direction of v1is the gradient direction of the gradient magnitude, and is also the direction of the vertical edge; the direction of v2is consistent with the direction of the edge. v1is perpendicular to v2.

2.3Application example analysis of image coherent attribute

We have selected three different typical models: a regular geometric model, a near parallel fan-form model and an irregular model. We get the coherent attribute of three models.

From Figs.2-4, we can see that coherent attri-bute with big values is the edge of the image, and no matter what kind of image, the edge with obvious co-lor difference is displayed through the coherent attri-bute. Finally, we achieve the automatic edge detection.

3Formation edge and dip attribute extraction

3.1 Gradient structure tensor producing

The gradient structure tensor generation is divided into two steps (Tang, 2012)：

First, calculate the gradient of seismic data in two directions ∂u/∂x and ∂u/∂y. We use the convolution between seismic data and derivative of Gaussian kernel function ∂G/∂x and ∂G/∂y to replace the gradient of seismic data. The Gaussian kernel function is:

(7)

Where, xjand yjare jth trace analysis points of derivation along thexaxis andyaxis, respectively. σ is the scale factor.

Second, gradient structure tensorTis obtained by multiplying the gradient vector and its transpose, every element of tensor is smoothed by using Gaussian kernel function for the second timeT. The expression ofTis given as following:

T=ggT

(8)

Where

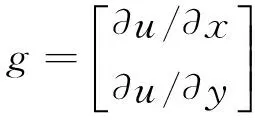
(9)

Tsis as following：

(10)

Gis given by Eq. (7).

The structure tensor in Eq. (10) is done through the method of eigenvalue decompositon.

TSv=Λv

(11)

Where, Λ is diagonal matrix, the values on the dia-

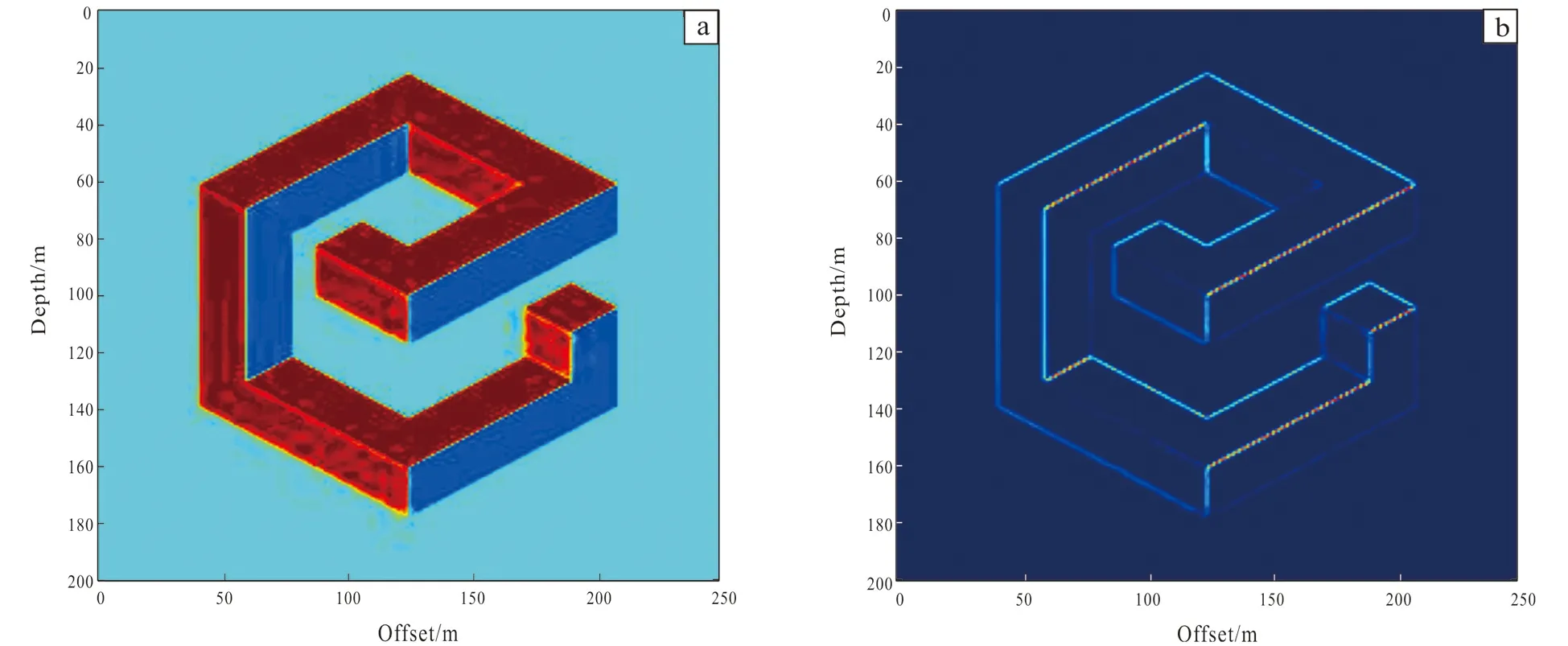
Fig.2　A regular geometric figure

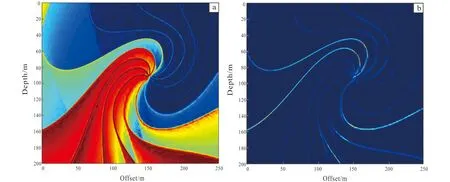
Fig.3　A subparallel fan-form figure

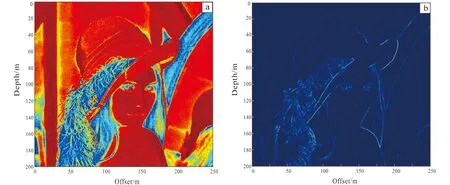
Fig.4　An irregular figure

gonal are the eigenvalues which are λ1and λ2, and they are arranged from large to small. v represents the eigenvector matrix. The column vectors represent the corresponding eigenvectors of eigenvalues, which are e1and e2.

We give the function of dip (Fang, 2012):

(12)

3.2Edge and dip attributes extraction of academic seismic model

The coherence property derived from the compu-ter image processing can be applied to the seismic profile to extract the edges of the formations. In this paper, we use a synthetic seismic record model, which contains a number of inclined formations on the top, an unconformity, a fault and a number of sinusoidal formations shown in Fig.5.

Fig.5a is the original seismic profile and Fig.5b is the coherent attribute image. Several high-impe-dance formations are well be extracted and the formation with little change in impedance is eliminated. Then we extract the main edges of formation.

But in the original seismic profile, a big fault in the image coherent attribute is not clearly displayed. Then coherent attribute of computer image processing cannot meet our need, so we use the dip of the seismic geometric property in the image to extract the dip angle.

In Fig.6, we can see that the parallel formation on the top is yellow, and the slope is about 20 degrees, which coincides with the dip in original seismic image of the model. The changes of area color in anticline and syncline are also consistent to the dip changes of the area. The influence of the formation edges is neglected, and a big fault is extracted. Because the fault is the place where is an occurrence of sliding, and its dip must have a big change. But the continuity of fault and surrounding is still relatively good, so we cannot use the coherent attribute to extract. This is very helpful for us to identify the fault automatically.

We can give p image in Fig.7 throughp=v1(x).

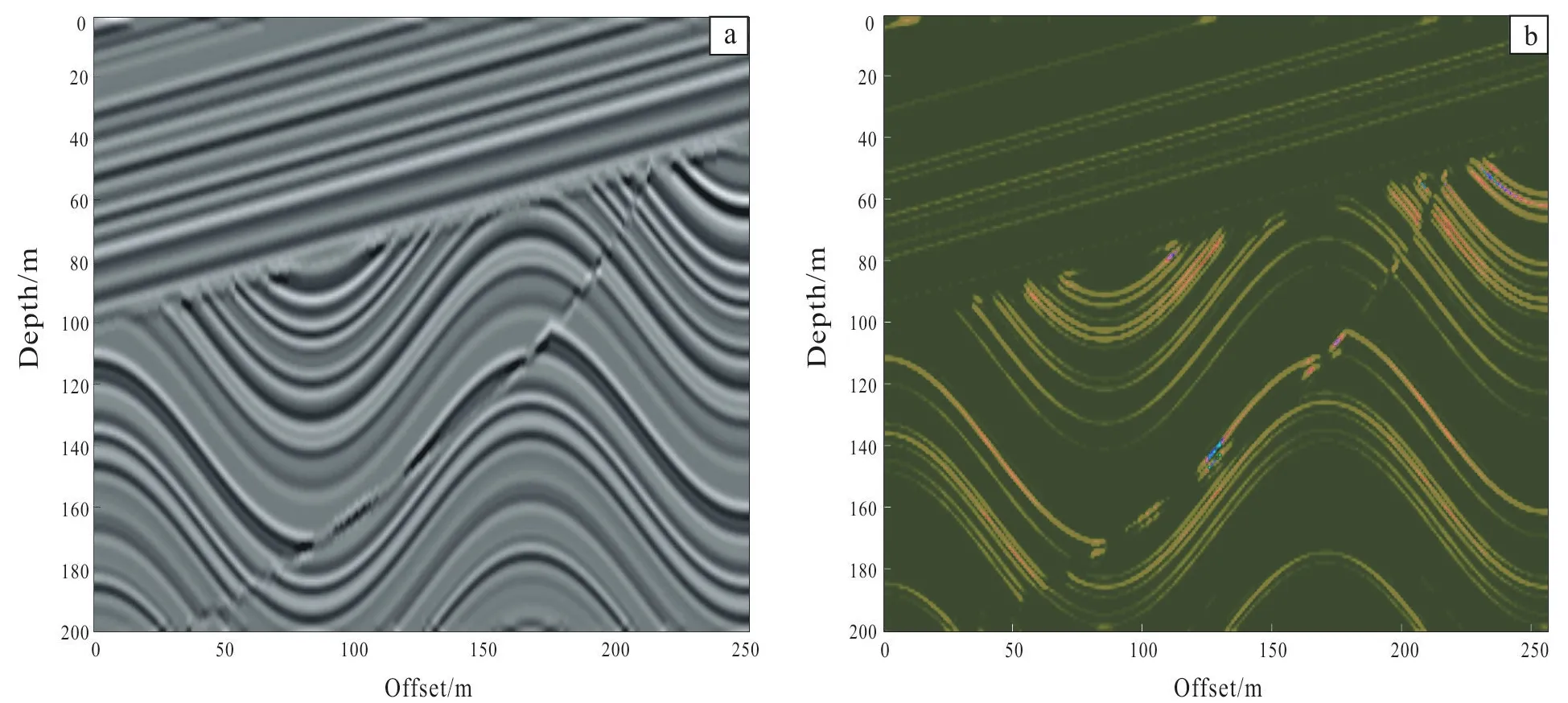
(a) Original seismic section image; (b) coherent attribute image.Fig.5　Contrast between original seismic section image and coherent attribute image

3.3Influence of noise on attributes extraction

At present, the detection of image edge is mainly based on calculating the first derivative and second derivative of image data, but the effect of noise on the derivative calculation is very large, so we can only use the appropriate denoising method to extract the image edge and dip attribute more clearly and effectively. In many edge detection methods, the Gaussian filter is used as the most basic denoising method. But the denoising processing will smooth the gradient values. So it is important to select the size of Gaussian kernel function window and the value of Gaussian kernel.

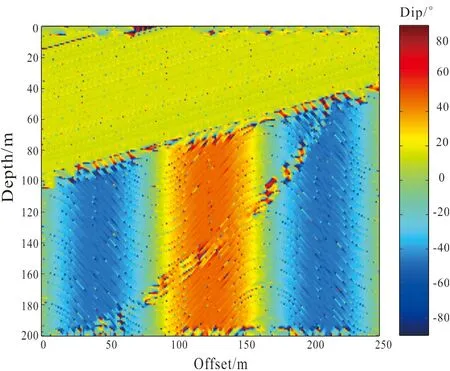
Fig.6　Dip attribute image

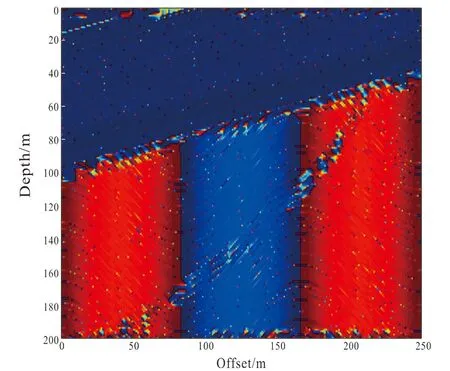
Fig.7　Visual dip attribute image

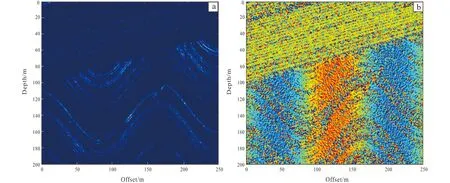
(a) Noisy coherent image; (b) dip attribute image.Fig.8　Noisy coherent and dip attribute images

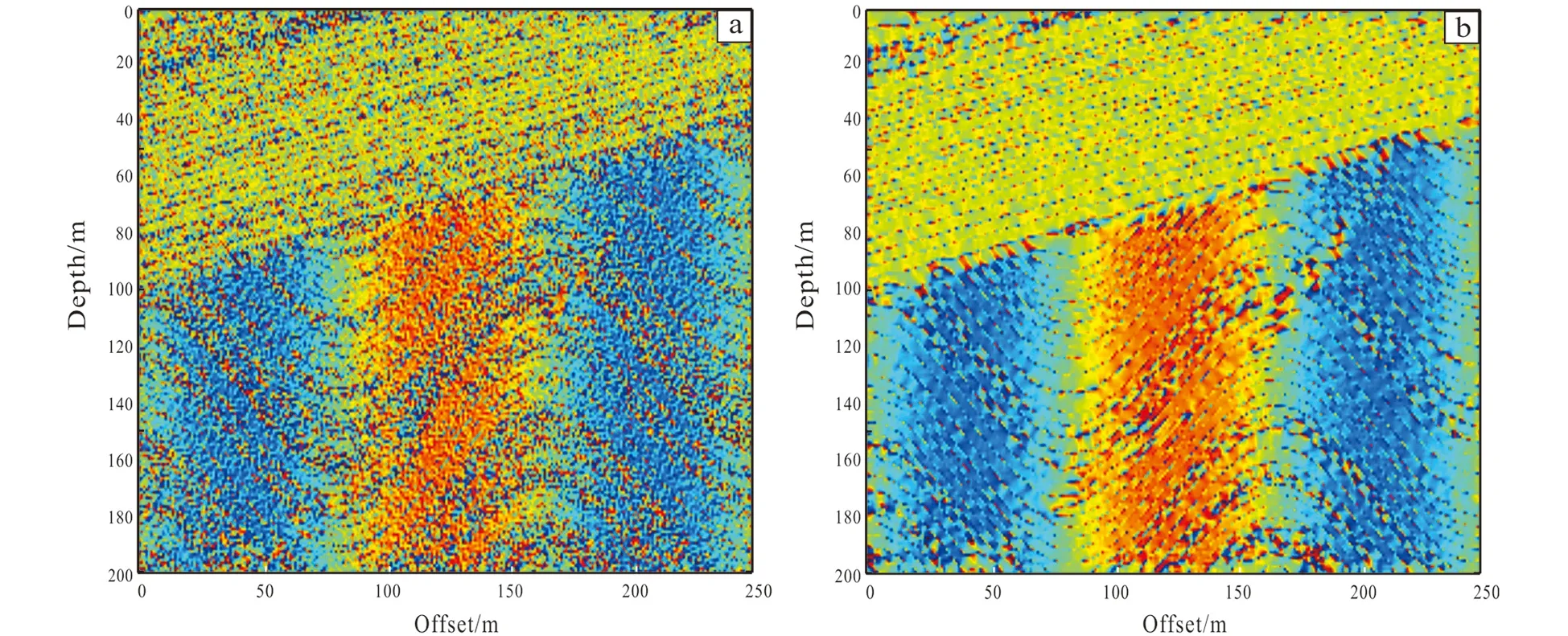
Fig. 9　Dip attribute image before and after denoising

We add random noise into the original seismic model, and analyze the influence of noise on coherent attribute and dip attribute:

Due to the influence of noise, the middle formation in Fig.8a is weakened, while in Fig.8b the changes of dip can only be seen in the overall trend without order. The clear fault which is originally extracted is also buries in the noise..

Using the convolution of Gaussian kernel function ∂G/∂x and ∂G/∂y to replace ∂u/∂x and ∂u/∂y, the coherent attribute and the dip attribute of the image before and after denoising are given as following:

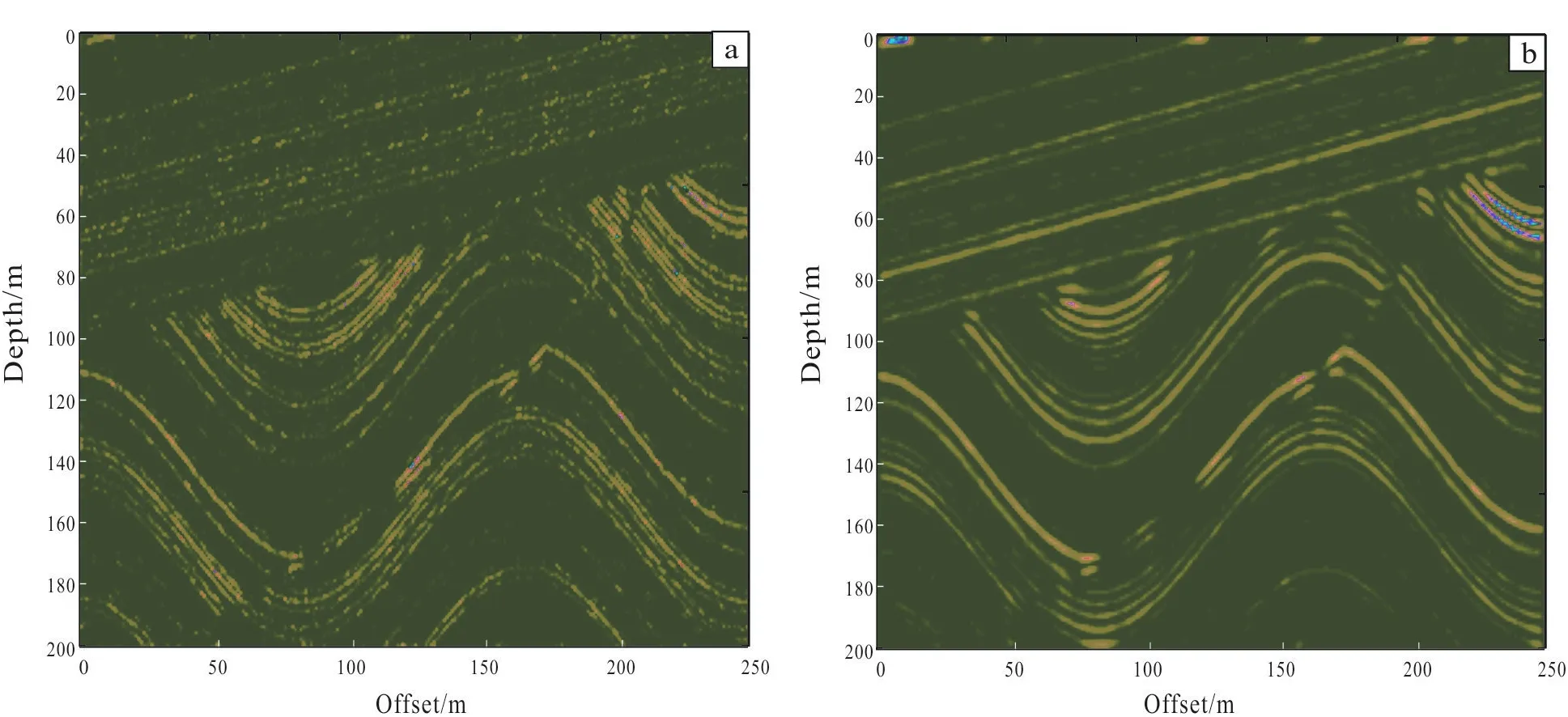
Fig.10　Coherent attribute image before and after denoising

In Fig.9 the strike of the fault can be seen and in Fig.10 the intermediate formation edges which are weakened by noise are redisplayed. It can be concluded that the convolution of Gaussian kernel smoothing function can remove the noise and recover the original features of the formation better.

4Conclusions

(1) The seismic geometric attributes are very important in the field of seismic exploration. It is the foundation of seismic interpretation. It reflects the underground geological structure, and it is of great significance to find oil and gas. Combined the data from the window which uses analysis point as the center, the geometric properties can be extracted.

(2) The coherent attribute from the edge detection technique can be applied to extract the formation edges in the seismic profile, enhance the edges of formation which have a great difference in impedance and weaken the edges of formation which have a little difference in impedance. The dip attribute can extract the inconspicuous fault in the syncline and anticline.

(3) Gaussian filter can remove noise, but it can not remove non-edge points with big gradient value. So we also need non-local maximum restraining technology to remove those non-edge points.

References

Bigün J, Granlund G H, Wiklund J. 1991. Multidimensional orientation estimation with applications to texture analysis and optical flow.IEEETransactionsonPatternAnalysis&MachineIntelligence, 13(8): 775-790.

Brox T, Weickert J, Burgeth B,etal. 2006. Nonlinear structure tensors.Image&VisionComputing, 24(1):41-55.

Chen C L, Liu Y, Liu C. 2011. Volcanic rock recognition by local seismic attribution.GlobalGeology, 30(4):661-665.

Deriche R. 2002. Diffusion PDE’s on vector-valued images: local approach and geometric viewpoint.IEEESignalProcessingMagazine, 19(5):16-25.

Duan R L, Li Q X, Li Y H. 2005. Summary of image edge detection.OpticalTechnique, 31(3): 415-416.

Fang L C. 2012. Research and application on bilateral filter gradient structure tensor based 3D image texture: master’s degree thesis. Sichuan: University of Electronic Science and Technology of China.

Förstner W, Gülch E. 1987. A fast operator for detection and precise location of distinct points, corners and centres of circular features//Isprs Intercommission conference on Fast Processing of Photogrammetric Data, 281-305.

Jähne B. 1993. Spatio-temporal image processing: theory and scientific applications.LectureNotesinCompScience, 212-233.

Li X G, Xu G Q, Qi Z L,etal. 2013. Qualitative identification of fault-related fracture (FRF): principle and its application.JournalofJilinUniversity:EarthScienceEdition, 43(6):1780-1786.

Medioni G, Lee M S, Tang C K. 2000. A computational framework for feature extraction and segmentation. Amsderstam: Elseviers Science, 251-260.

Tang C Y. 2012. Research and application on local structure based seismic geometric attributes: master’s degree thesis. Sichuan: Southwest Jiaotong University.

Yang Z X, Lu F, Li Y S. 2002. Computation of image gra-dient and divergence and their application to edge detection of noisy images.ActaScientiarumNaturaliumUniversitatisSunyatseni, 41(6): 6-9.

Zhang J H, Dong M, Zhou Z X,etal. 2007. Research and application on gradient structure tensor based coherent method.NaturalGasIndustry, (S1):381-383.

Zheng Y H, Pan Y, Heng P A,etal. 2008. The trace-based nonlinear structure tensor.JournalofComputer-AidedDesign&ComputerGraphics, 20(2): 259-266.

doi:10.3969/j.issn.1673-9736.2016.02.07

Article ID: 1673-9736(2016)02-0109-08

Received 16 October 2015, accepted 5 December 2015

Support by National Natural Science Foundation of China(No.41274120).

* Corresponding author (Email:sun_jg@jlu.edu.cn)