Comparison of finite difference and pseudo-spectral methods in forward modelling based on metal ore model of random media

LIU Dongyu, HAN Liguo, ZHANG Pan and XU Dexin

CollegeofGeo-ExplorationScienceandTechnology,JilinUniversity,Changchun130026,China



Comparison of finite difference and pseudo-spectral methods in forward modelling based on metal ore model of random media

LIU Dongyu, HAN Liguo, ZHANG Pan and XU Dexin

CollegeofGeo-ExplorationScienceandTechnology,JilinUniversity,Changchun130026,China

Abstract:With more applications of seismic exploration in metal ore exploration, forward modelling of seismic wave has become more important in metal ore. Finite difference method and pseudo-spectral method are two important methods of wave-field simulation. Results of previous studies show that both methods have distinct advantages and disadvantages: Finite difference method has high precision but its dispersion is serious; pseudo-spectral method considers both computational efficiency and precision but has less precision than finite-diffe-rence. The authors consider the complex structural characteristics of the metal ore, furthermore add random media in order to simulate the complex effects produced by metal ore for wave field. First, the study introduced the theories of random media and two forward modelling methods. Second, it compared the simulation results of two methods on fault model. Then the authors established a complex metal ore model, added random media and compared computational efficiency and precision. As a result, it is found that finite difference method is better than pseudo-spectral method in precision and boundary treatment, but the computational efficiency of pseudo-spectral method is slightly higher than the finite difference method.

Key words:metal ore; random media; finite difference method; pseudo-spectral method

0Introduction

In recent years, with increasing applications of seismic exploration in metal ore exploration, forward simulation of seismic waves in complex media of metal ore becomes more and more important. Faced with this situation, we added random media in complex metal ore and used finite difference method and pseudo-spectral method to compare.

Xi & Yao (2001) first constructed a two-dimensional random media model. Yin & Liu (2011) stu-died two-dimensional random media further and made staggered-grid finite difference modelling. Wang (2008) carried out three-component model forward modelling using monoclinic random model. Lian & Han (2011) studied random media seismic forward modelling of steep metal ore.

Finite difference method is a widely used numerical simulation in seismic exploration, its basic idea is to use discrete finite difference scheme to instead of continuous infinite differential scheme. Alterman & Karal (1968), who first used explicit finite-difference scheme, have got discrete numerical solution of la-yered media of second order elastic wave equation. Now, the finite difference method is already quite mature, many Chinese scholars also conducted deep study in this area. Dongetal. (2000) combined high-order finite difference and staggered-grid, which weakened the numerical dispersion effectively and improved the accuracy without increasing the memory. Yangetal. (2014) deduced the derivative of any order of staggered-grid finite difference scheme, which enhanced the stability and improved the accuracy.

Pseudo-spectral method is also a common method in forward modelling simulation of seismic wave field, it takes account of precision and computational efficiency. Early pseudo-spectral method was limited to development and research of two-dimensional algorithm programs. Pseudo-spectral method was used in acoustic wave equation simulation by Dan & Baysal (1982). In the late 1980s, Reshefetal.(1988) made wave propagation simulation in homogeneous media by three-dimensional acoustic wave equation and tree-dimensional elastic wave equation. With the development of technology, practical problems in seismic exploration have become complex gradually, seismic wave propagation in complex formation has caused increasingly attention.

1Random media model

In seismic exploration, generally the medium is non-uniform, and there are a large number of irregular and small-scale abnormal bodies. With the increasing precision of dealing with complex data, higher frequency is more and more used, and small-scale abnormal bodies apparently have a negative effect on propagation of seismic waves. But it is hard for traditional models to accurately describe this kind of abnormal bodies. Faced with this issue, we selected random medium model based on statistical theory to describe this phenomenon.

Two-dimensional autocorrelation function includes exponential type, Gaussian type and Von Karman type functions. Comparing with Gaussian-type related functions, exponential-type and Von Karman type related functions have more advantageous capacity on depicting multiscale random medium and simulating the real situation of underground. We use Von Karman type related functions.

(1)

Whereaandbare autocorrelation length of random medium on the orientation ofx,yand z corresponding to autocorrelation functions, respectively:Kνis the third kind Bessel function ofνrank, 0<ν<1. Here we set a=25 and b=10.

a. Simple fault model; b. combined with Von Karman type random media and simple fault model.Fig.1　Fault velocity model

Fig.1a is a simple fault model, the size is 2 000 m*2 000 m, Fig.1b is a three-layer random model, which has the same size with Fig.1a, and is combined with Von Karman type random medium and simple fault model.

2Finite difference forward modelling

This paper uses time second order and spatial fourth order difference scheme. Consider two-dimensional acoustic wave equation:

(2)

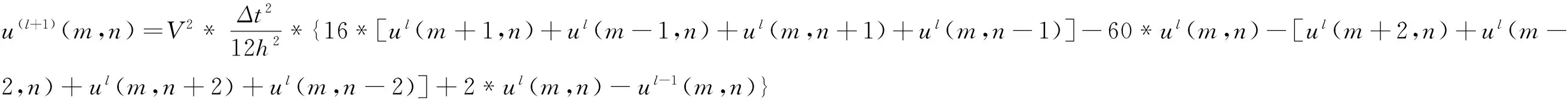
(3)

We choose Perfectly Matched Layer (PML) as boundary conditions. With respect to acoustic wave equation (2), corresponding control equation of PML is:

Whereu1,u2,A1andA2are introduced intermediate variables,d1(x) andd2(x) are attenuation coefficient on the orientation ofxandz, respectively.

The basic approach is shown in Fig.2:

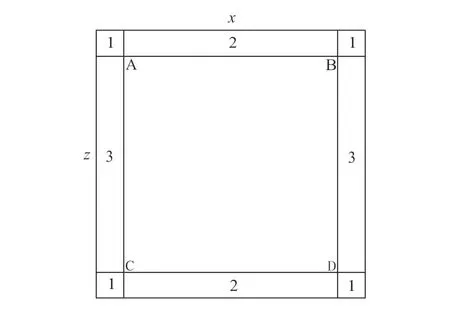
Fig.2　PML absorbing boundary schematic

A, B, C and D are the research areas, PML is added to its periphery. In section 1, setd1(x)≠0 andd2(x)≠0;in section 2,d1(x)=0 andd2(x)≠0; in section 3,d1(x)≠0 andd2(x)=0. When the waves propagate from interior to PML, the reflections do not occur; when they propagate in PML, the reflections do not occur; when they arrive at the boun-dary of totally marched layer, wave field is approximately zero, the reflections do not occur.

3Pseudo-spectral method forward modelling

Similar to finite difference method, this paper is still using two-dimensional acoustic wave equation.

(4)

Wheres=s(x,z,t) is the source term.

(5)

Use Fourier pseudo-spectrum method to calculate space differentiation. Take partial derivative to x for example.

Finally we obtain:

4Comparison of two forward modelling methods

Fig.3a and Fig.3b are simulated wave field of the velocity model showing in Fig.1a, which use finite difference method and pseudo-spectral method, respectively. It is easy to confirm that both methods can reflect the layer information precisely. In compa-rison, there is some dispersion problems in finite difference method to some extent, while pseudo-spectral method has a little boundary effects (same with the PML absorbing boundary).

Fig.4a and Fig.4b are simulated wave field of Fig.1b, which use finite difference method and pseudo-spectral method, respectively. Due to the unorganized random perturbation, useful information of wave field becomes unobvious, the reflected energy also decreased, while the layer information is still easy to distinguish. Since the chosen model is relatively simple, the two forward methods both can obtain many detailed information and similar simulation results for the complex scattering caused by random media.

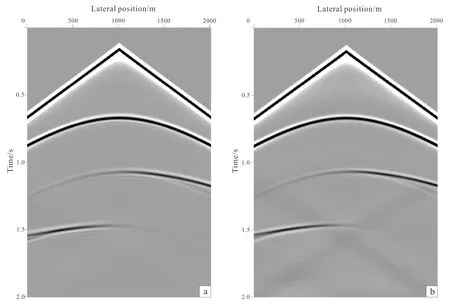
a. Finite difference method wave field; b. pseudo-spectral method wave field.Fig.3　Comparison of fault model wave field

5Comparison of forward effect in metal ore random media model

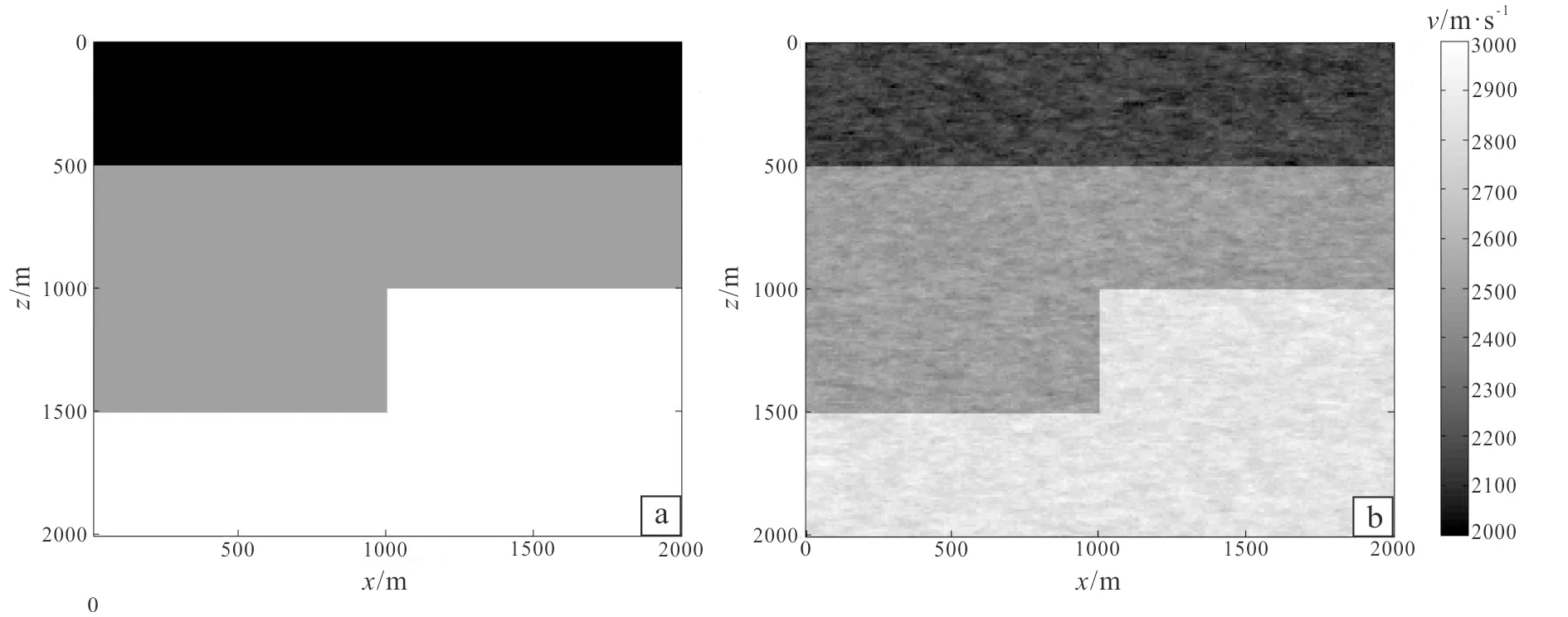
Using the metal ore model shown in Fig.5a, which contains complex configuration information, we can hardly find lamellar results, and the red high-speed area in the middle of the model represents metal ore target body. In order to study this complex model well, higher requirements of the precision and efficiency in forward model are necessary. If the precision is low, a lot of the details of construction will not be reflected, and the image quality of the target body will decreased. If the efficiency is low, some methods such as full waveform inversion which dependent on forward method will not be implemented. Fig.5b is the metal ore model adding random medium, which is closer to the actual complex situation, increasing the influence on the wave field of scattering point. It needs further requirements on the precision and efficiency of forward calculation.

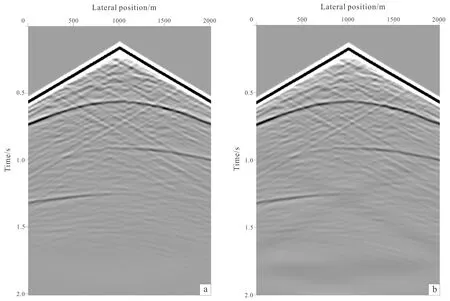
a. Finite difference wave field; b. pseudo-spectral method wave field.Fig.4　Comparison of fault random model wave field

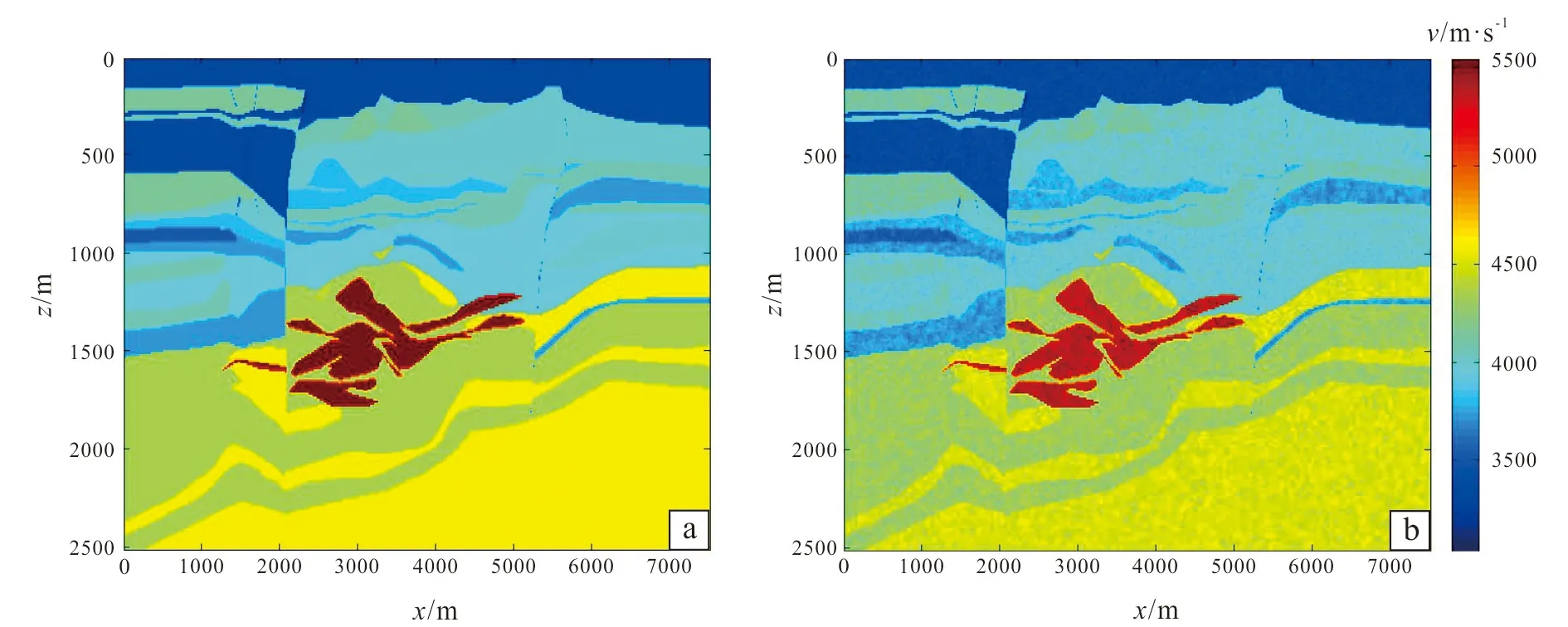
a. Metal ore model; b. metal ore model of random media.Fig.5　Metal ore velocity model

We get seismogram Figs.6,7 using the finite difference method and pseudo-spectral method to run the forward model, in which Fig.6a and Fig.7a represent finite difference wave field, Fig.6b and Fig.7b represent pseudo-spectral wave field. Both the metho-ds can obtain simulation results of high accuracy for Fig.5 which has no random interference (Fig.6a, b). The reflection event and details obtained by the two methods are clear and similar, except for the border interference in pseudo-spectral method. After the velocity model is added in random interference, the detail scattering information of the two methods differs obviously. Compared with Fig.7b, Fig.7a has more information about linear event, which represents the scattering of scatterers. And the border effect is difficult to deal with in pseudo-spectral method, while in complex models the impact of the wave field can not be ignored.

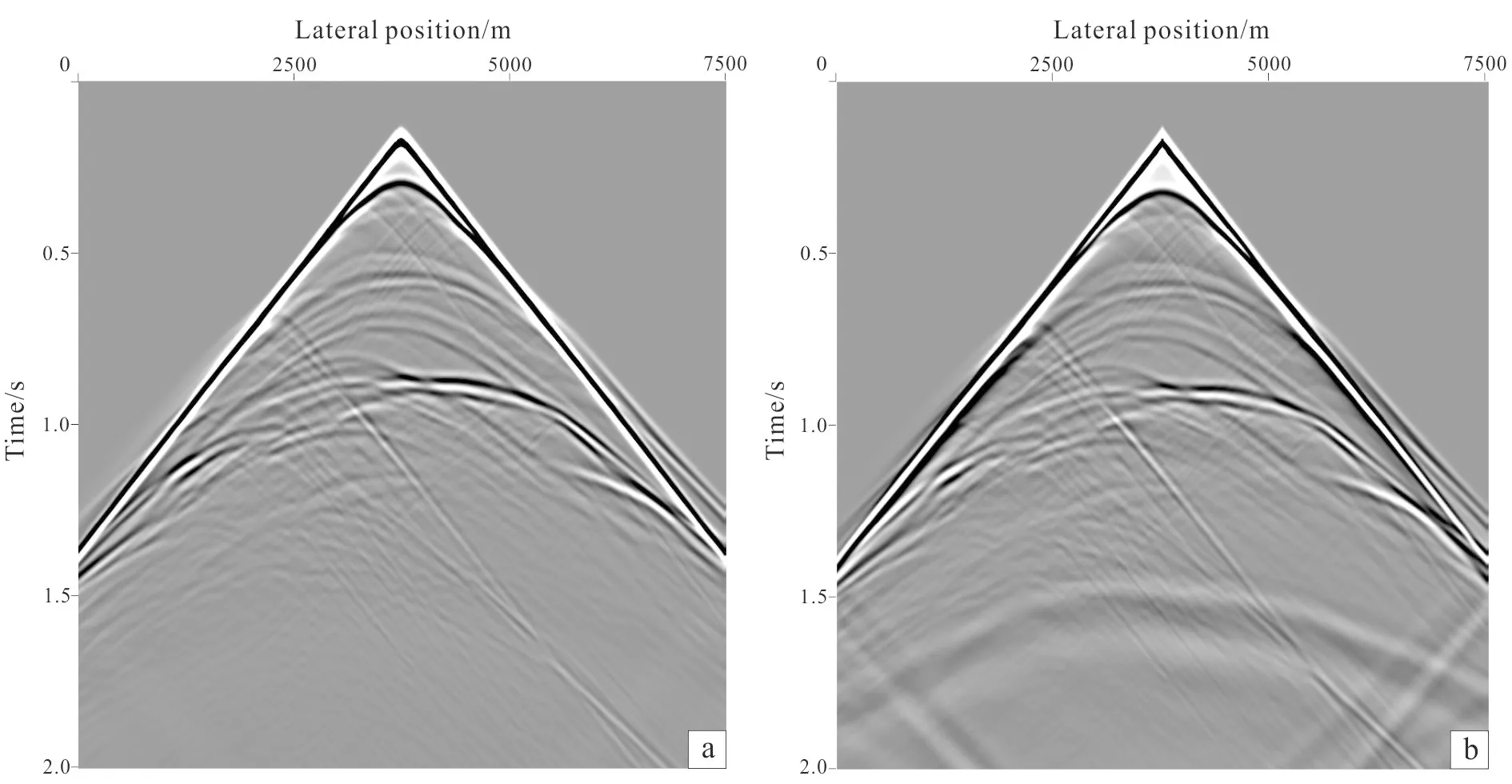
a. Finite difference method wave field; b. pseudo-spectral method wave field.Fig.6　Comparison of metal ore model wave field

a. Finite difference method wave field; b. pseudo-spectral method wave field.Fig.7　Comparison of random metal ore model wave field

6Conclusions

In this paper, the precision and efficiency of finite difference method and the pseudo-spectral method in forward model are compared in the metal ore model of random media. For the simple model, two methods both can reflect the reflection information of the interface and the diffraction event due to random perturbations. For the complex media, especially after the random media involved, the finite difference method has an obvious advantage in precision, and the record contains a lot of detailed information. The boundary is more difficult to handle in pseudo-spectral method than that in finite difference method. As to the computational efficiency, pseudo-spectral method is slightly supervisor to the finite difference method. The calculation efficiency of finite difference method can be close to or even better than the pseudo-spectral method after using convolution and matrix. In conclusion, in the forward modelling process of metal ore complex media, two methods both can be used for general migration image; in the full waveform inversion which strongly dependents on the precision and efficiency of the forward method, finite difference method is recommended.

References

Alterman Z, Karal F C. 1968. Propagation of elastic wave in layered media by finite difference methods.BulletinoftheSeismologicalSocietyofAmerica, 58(1):367-398.

Dan D K, Baysal E. 1982. Forward modelling by a Fourier method.Geophysics, 47(10): 1402-1412

Dong L G, Ma Z T, Cao J Z,etal. 2000. A Staggered-grid high-order difference method of one-order elastic wave equation.ChineseJournalofGeophysics, 43(3): 411-419.

Lian Y G, Han L G. 2011. The study of random media seismic forward modelling of steep metal ore.ComputingTechniquesForGeophysicalandGeochemicalExploration, 33(4): 364-367.

Reshef M, Dan D K, Edwards M,etal. 1988. Three dimensional elastic modelling by the Fourier method.Geophy-sics, 53(9):1184-1193.

Wang E L. 2008. The forward modelling and character analysis for complex media based on anisotropic media: PhD thesis. Changchun: Jilin University.

Xi X, Yao Y. 2001. 2-D random media and wave equation forward modelling.OilGeophysicalProspecting, 36(5): 546-552.

Yang Q J, Liu C, Geng M X,etal. 2014. Staggered grid finite difference scheme and coefficients deduction of any number of derivatives.JournalofJilinUniversity:EarthScienceEdition, 44(1): 375-385.

Yin X X, Liu Y. 2011. Random medium 2-D modelling and its wave field analysis.OilGeophysicalProspecting, 46(6): 862-872.

doi:10.3969/j.issn.1673-9736.2016.02.06

Article ID: 1673-9736(2016)02-0102-07

Received 28 October 2015, accepted 6 January 2016

Supported by the National “863” Project (No. 2014AA06A605).