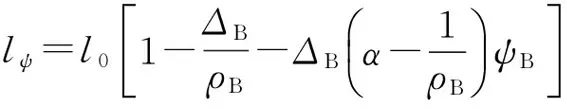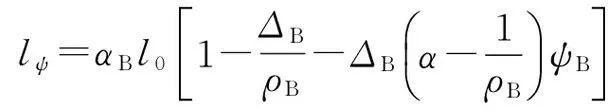液体随行装药内弹道计算中液滴喷雾模型分析

刘　怡,余永刚

(南京理工大学 能源与动力工程学院,南京210094)



液体随行装药内弹道计算中液滴喷雾模型分析

刘怡,余永刚

(南京理工大学 能源与动力工程学院,南京210094)

摘要:随行装药是一种能在最大膛压不变的条件下,通过提高膛压曲线充满系数,从而提高弹丸初速的新型技术。针对30 mm液体随行装药结构,建立内弹道零维模型,其中随行液体药采用喷雾燃烧模型。为了寻找较好的液滴直径计算模型,分别采用定直径液滴模型、气动破碎的变直径液滴模型以及破碎液滴直径呈正态分布的模型进行内弹道数值计算。结果表明,在最大膛压保持不变的条件下,3种液滴直径模型的数值计算结果均与实验结果基本吻合,液滴直径呈正态分布的模型计算结果最接近实验值。

关键词:液体随行装药;喷雾燃烧;液滴直径;数值计算

随着时代的发展和科技的进步,未来战争对火炮性能的要求越来越高。炮口初速是衡量火炮性能的一项重要指标,但通过常规装药技术来大幅度提高炮口初速已非常困难,为了满足未来战争对高初速火炮的需求,随行装药技术研究受到重视。随行装药技术能够在保持最大膛压不变的情况下有效提高炮口初速。随行装药技术首次是由德国人兰维勒于1939年提出的,随行装药方案有固体随行和液体随行2种。上世纪八十年代,美国的Bulman和Irvin等[1-2]将液体发射药用于随行装药,得到了较高的炮口初速。国内很多学者对液体随行装药进行了探索和研究,余永刚等[3]在1997年对30 mm火炮液体随行装药进行实验,首次在火炮上实现随行效应;周彦煌等[4]采用多孔介质整装式液体随行装药方案,对随行装药的3项关键技术进行研究;陆欣等[5-6]采用整装式液体随行装药进行了实验研究,随后建立了随行装药的两相流数值模型,数值计算结果与实验结果相比有较好的一致性;邹华等[7]于2013年对差动自喷弹药的新型液体随行装药方案进行了数值模拟,结果显示弹丸初速有所提高。

本文针对30 mm弹道炮,对液体随行装药的内弹道过程进行数值计算,其中液体随行药采用喷射雾化燃烧模型。液滴直径分别采用3种模型进行仿真计算,即定直径液滴模型、气动破碎的变直径液滴模型、破碎液滴直径呈正态分布的模型。将数值计算结果与实验结果进行比较,分析哪种模型更接近实验工况。

1液体随行装药内弹道模型

1.1物理模型

图1为液体随行装药喷射结构示意图。

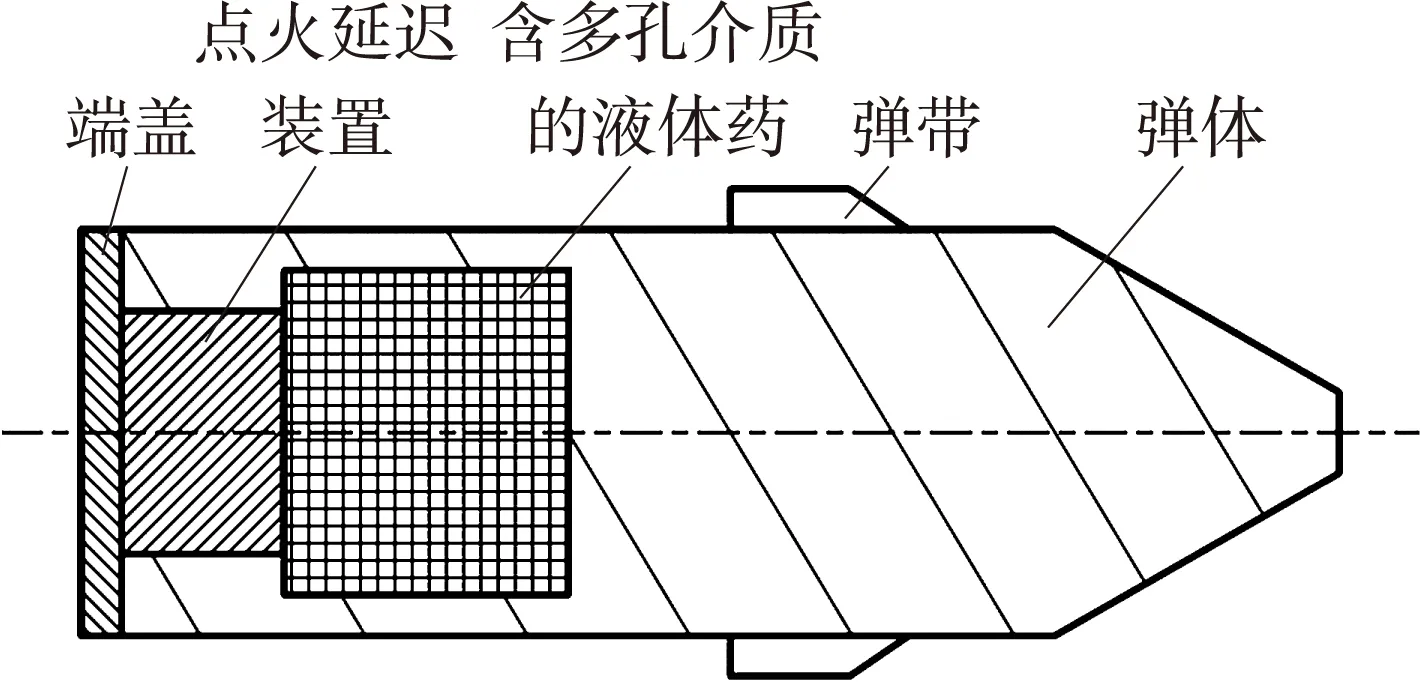
图1　液体随行装药喷射结构示意图

如图1所示,液体随行装药最初装在弹丸尾部的贮液室中,与弹丸一起在膛内运动。主装药燃烧,弹后空间压力不断升高,当点火延迟装置打开后,高压燃气喷入贮液室,挤压多孔介质,液体药从多孔介质喷入弹后空间,雾化成液滴群并燃烧。通过主装药和随行装药共同燃烧提供能量,弹丸运动到炮口会产生较高的初速。

液体随行装药喷射雾化燃烧模型的建立采用的基本假设如下:

①不考虑主装药的点火过程,以30 MPa的挤进压力作为弹丸的启动压力,达到启动压力以后,弹丸开始运动;

②不考虑液体随行药的点火过程,当点火延迟装置打开后,随行液体药开始喷射燃烧;

③主装药为固体药,遵循几何燃烧定律和指数燃速关系;

④随行药为液体药,喷射雾化液滴为球形,遵循指数燃速关系;

⑤发射过程中,各种能量损失通过次要功系数间接修正。

1.2数学模型

主装药燃速方程和形状函数为

(1)

(2)

式中:下标B代表主装药,下标s代表减面燃烧阶段;z为火药相对厚度;t为时间;u1为燃速常数;n为燃速指数;e1为火药肉厚的一半;p为膛压;ψ为火药已燃百分比;χ,λ,μ为火药形状特征量;zk为火药分裂后碎粒全部燃烧完时的燃去相对厚度。液体随行装药的燃速方程和形状函数要根据不同的液滴直径模型建立。

液体随行药喷射雾化燃烧,喷入燃烧室的液滴按照时间先后顺序划分为N组液滴群,相关的喷射方程为

(3)

(4)

(5)

(6)

根据贮液室中液体药状态方程,得到液体药密度表达式为

(7)

式中:ρL0为液体药初始密度,pL0为贮液室中的初始压力,K为体积模量,C为体积模量系数。

弹丸速度方程和运动方程为

(8)

(9)

式中:l为弹丸运动距离,v为弹丸运动速度,φ为次要功计算系数,S为炮膛横断面面积,m为弹丸质量。

燃气状态方程为

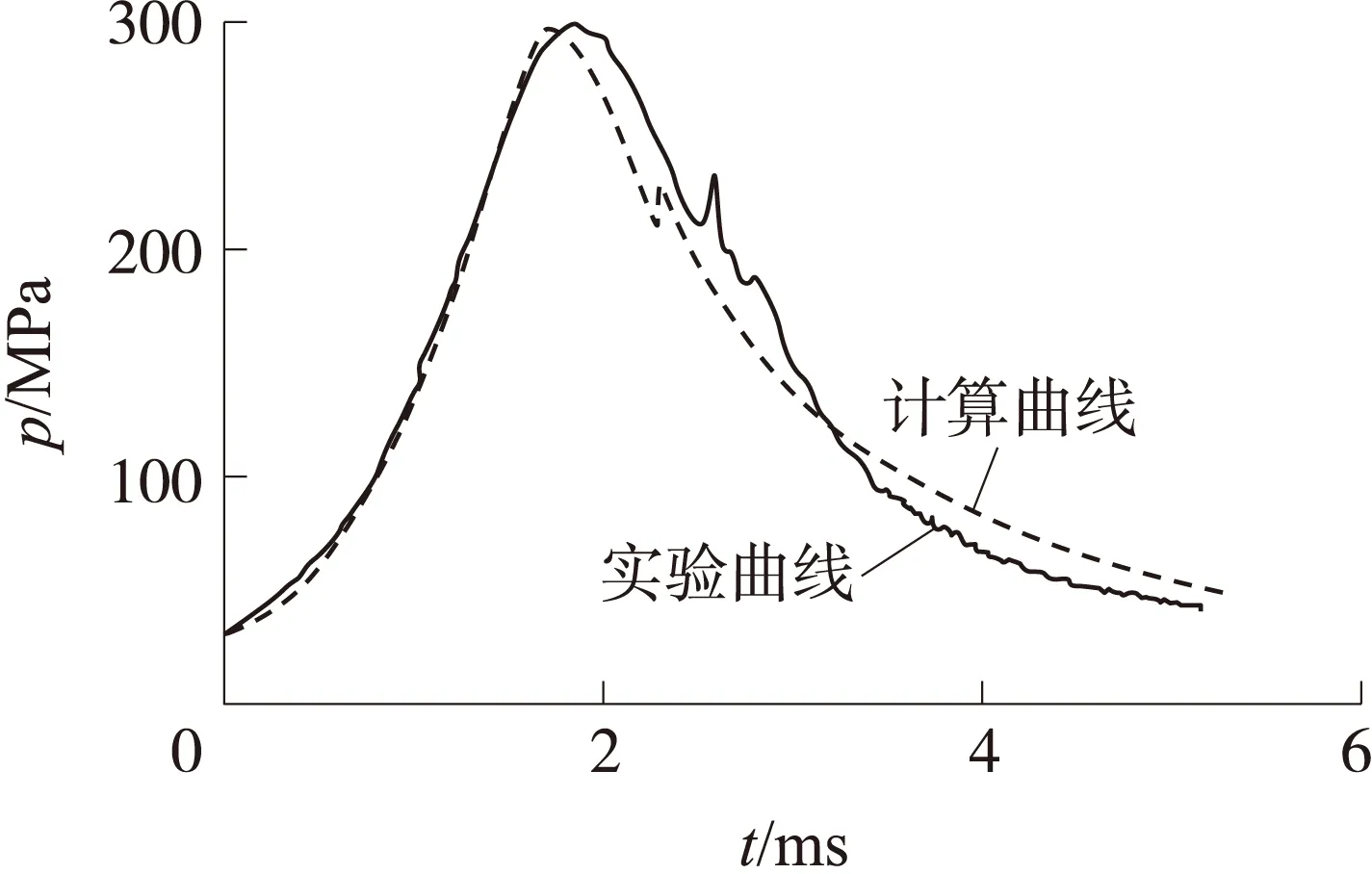
Sp(l+lψ)=fBωBψB+fLωLψL-

(10)

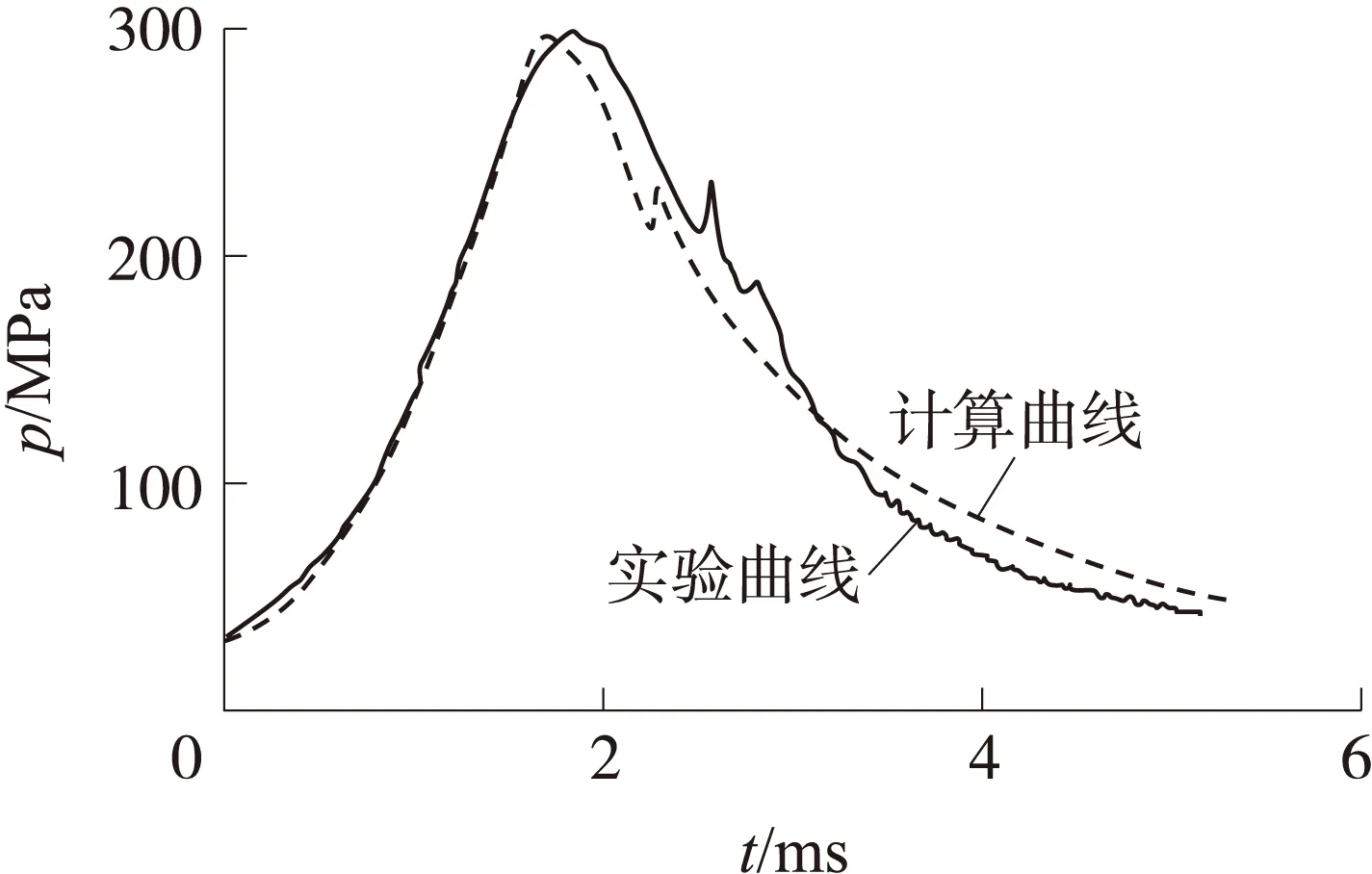
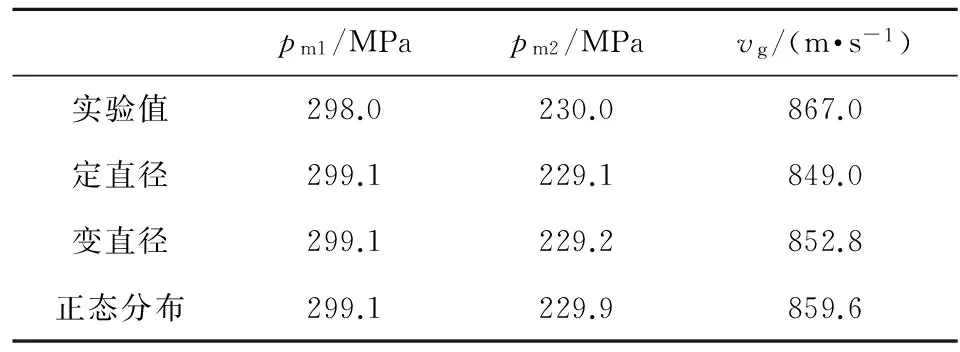
当t

当t≥tD时,有:

式中:θ=k-1,k为绝热指数;f为火药力;l0为药室容积缩径长;α为余容;Δ为装填密度;tD为随行药的点火延迟时间;αB和αL分别为主装药和随行装药占总装药的质量分数,有αB+αL=1。

随行液体药喷射到燃烧室中雾化成液滴群,有关液滴直径的尺寸分布,本文采用3种模型。

1)定直径液滴模型。

定直径液滴模型是指液体随行药从多孔介质喷出形成的所有液滴直径相同,即为同一常数。

液体随行药燃速方程和形状函数为

(11)

(12)

(13)

式中:rL0,i为第i组液滴群的液滴半径。

2)变直径液滴模型。

实际上,液体药喷射速度对液滴形成有一定的影响,液滴直径和液体药喷射速度的关系式为

式中:C1和n为常数,由实验确定。在单一喷孔直径为1～2 mm且液体喷射速度为30～300 m/s时,有经验关系式[8]:

(14)

液体随行药燃速方程和形状函数与定直径液滴模型中的燃速方程和形状函数一致,即式(11)和式(12)。

3)正态分布液滴直径模型。

液体燃料的喷射雾化过程是比较复杂的。液体药射流破碎,雾化为大量液滴,液滴之间有相互作用,聚并或者碰撞形成新的液滴,喷射的液滴直径尺寸呈现一个分布,通常采用正态分布。

假设喷射液滴的直径符合一维正态分布,其概率密度为

(15)

喷入燃烧室的液滴按照时间先后顺序划分为N组液滴群,将每一个时刻喷出的液滴群按照液滴直径离散为N′组,且每个时刻喷出的液滴群直径符合正态分布。被离散后的每一组液滴的直径作为计算单位,记为dij,符合一维正态分布概率分布公式:

(16)

(17)

(18)

(19)

(20)

式中:rL0,ij为第i组液滴群离散后的第j组液滴群的液滴半径,aj为第j组液滴群的相对质量,有:

2数值计算结果与分析

2.1数值计算参数

针对30 mm液体随行装药的结构体系进行数值模拟,其中主装药采用5/7多孔火药,随行药采用OTTO-Ⅱ液体火药。计算所用的参数如表1所示,表中,V0为燃烧室容积,VL0为贮液室容积,lg为炮管身长。

表1　数值计算所用的内弹道参数

为了寻找最符合实验工况的液滴直径模型,对3种液滴直径模型进行数值计算,计算过程中采用相同的初始压力和装填结构参数。

2.23种模型的数值计算结果与分析

联立式(1)～式(13),并用程序计算,得到定直径液滴模型的内弹道数值计算结果。图2是数值计算得到的膛压随时间变化的p-t曲线和实验的p-t曲线的对比图。

图2　定直径液滴模型数值计算与实验所得p-t曲线对比图

如图2所示,定直径液滴模型数值计算所得的p-t曲线与实验所得p-t曲线的变化趋势基本一致,都出现了第二压力峰值,两条曲线基本吻合。数值计算过程是从弹丸挤进炮膛到弹丸出炮口为止,并没有考虑点火过程,所以得到的p-t曲线图起点为启动压力30 MPa。

联立式(1)～式(14),经过程序运算得到变直径液滴模型的内弹道数值计算结果。膛压随时间变化的p-t曲线和实验的p-t曲线的对比图如图3所示。

图3　变直径液滴模型数值计算与实验所得p-t曲线对比图

从图中可以看出,两条p-t曲线基本吻合,数值计算求出的最大膛压与定直径液滴模型下求出的最大膛压值相等,液滴模型的改变对最大膛压值没有影响。

联立式(1)～式(11)、式(16)～式(20),经过程序运算得到液滴直径呈正态分布模型的内弹道数值计算结果。膛压随时间变化的p-t曲线和实验的p-t曲线的对比图如图4所示。计算曲线与实验曲线的吻合程度有所提高。

图4　液滴直径呈正态分布的模型数值计算与实验所得p-t曲线对比图

通过定直径液滴模型、气动破碎的变直径液滴模型以及破碎液滴直径呈正态分布模型的数值计算结果,可以看出它们与实验结果相比都基本吻合,说明3种液滴直径模型都是合理可行的。现将3种模型进行对比分析,找出最佳方案。3种液滴直径模型下p-t曲线的对比图如图5所示。

图5　3种直径模型下p-t曲线的对比图

当点火延迟装置没有打开时,主装药燃烧生成高温高压燃气推动弹丸运动,3种模型下p-t曲线前面部分是重合的;当达到点火延迟时间时,液体随行装药开始喷射燃烧,在不同的液滴直径模型下,p-t曲线后半部分有一定差别。

表2列出了3种液滴直径模型下的第一压力峰值pm1、第二压力峰值pm2和弹丸初速vg的具体数值,并与实验值进行了比较。可以看出,3种模型的第一压力峰值相同,第二压力峰值变化很小,而且都与实验结果基本吻合;3种模型下的弹丸初速误差分别为2%,1.6%和0.9%。可见,正态分布液滴直径模型的计算结果与实验值最接近,说明正态分布液滴直径模型是更接近实际工况的一种模型。

表2　3种模型下数值计算结果的对比

3结论

本文针对30 mm液体随行装药的内弹道过程进行了数值计算,可得出以下结论:

①数值计算得到的p-t曲线与实验所得的p-t曲线基本吻合,并且p-t曲线出现第二压力峰值,说明随行装药有效增大了膛压曲线下的面积，从而提高了弹丸初速;

②液滴直径模型对液体随行装药内弹道性能计算结果有一定影响,文中比较的3种液滴直径模型中,直径呈正态分布的模型最接近实际工况。

参考文献

[1]BULMAN M J.Liquid propellant weapon system:US,4852459[P].1987.

[2]IRVIN C S,KNAPTON J D.Test results from a two-stage traveling charge liquid propellant gun,AD-A224593[R].1990.

[3]余永刚,陆欣.30 mm火炮液体随行装药的实验研究[J].弹道学报,1997,9(3):91-93.

YU Yong-gang,LU Xin.Experimental research on liquid propellant traveling charge of 30 mm gun[J].Journal of Ballistics,1997,9(3):91-93.(in Chinese)

[4]周彦煌,余永刚.整装式液体随行装药关键技术研究[J].兵工学报,1997,18(3):226-229.

ZHOU Yan-huang,YU Yong-gang.On a novel concept in bulk-loaded liquid traveling charge[J].Acta Armamentarii,1997,18(3):226-229.(in Chinese)

[5]陆欣,周彦煌.整装式液体随行装药燃烧的实验与数值模拟研究[J].爆炸与冲击,1998,18(3):203-207.

LU Xin,ZHOU Yan-huang.Numerical simulation of bulk liquid traveling charge combustion[J].Explosion and Shock Waves,1998,18(3):203-207.(in Chinese)

[6]陆欣,周彦煌.整装式液体随行装药的两相流数值仿真[J].兵工学报,2001,22(1):27-30.

LU Xin,ZHOU Yan-huang.Numerical simulation of two-phase flow of bulk liquid traveling charge[J].Acta Armamentarii,2001,22(1):27-30.(in Chinese)

[7]邹华,陆欣,周彦煌.基于液体随行装药的高初速火炮内弹道理论研究[J].弹道学报,2013,25(3):75-78.ZOU Hua,LU Xin,ZHOU Yan-huang.Theoretical study on interior ballistics of high velocity gun based on liquid traveling charge[J].Journal of Ballistics,2013,25(3):75-78.(in Chinese)

[8]陆欣.新概念武器发射原理[M].北京:北京航空航天大学出版社,2015.

LU Xin.Emission principle of new concept weapons[M].Beijing:Beihang University Press,2015.(in Chinese)

Analysis of Droplet Spray Model for Interior Ballistic Calculation of Liquid Traveling Charge

LIU Yi,YU Yong-gang

(School of Energy and Power Engineering,Nanjing University of Science and Technology,Nanjing 210094,China)

Abstract:Traveling charge is a new technique to increase the muzzle velocity by improving the pressure curve coefficient under the same maximal pressure.For the structure of 30 mm liquid traveling charge,the zero-dimensional model was set up,and the liquid propellant adopted the method of spray atomized combustion.To find out a better numerical model of droplet diameter,the traditional fixed-diameter droplet model,the variable-diameter droplet model and the model of droplet diameter with normal distribution were applied respectively to numerically calculate the interior ballistics.The results show that the simulation results of three models agree well with experimental results respectively under the conditions of the maximum chamber pressure of traveling charge remaining unchanged,and the numerical model of droplet diameter with normal distribution is the best one of the three models.

Key words:liquid traveling charge;spray combustion;droplet diameter;numerical calculation

收稿日期:2016-01-21

作者简介:刘怡(1991- ),女,硕士研究生,研究方向为含能材料燃烧推进技术。E-mail:liuyi61mm@163.com。

中图分类号:TJ301

文献标识码:A

文章编号:1004-499X(2016)02-0074-05