基于摄动理论的纵向弹道修正方法改进

高　敏,张永伟,杨锁昌,吕　静

(军械工程学院 1.导弹工程系;2弹药工程系,石家庄 050003)



基于摄动理论的纵向弹道修正方法改进

高敏1,张永伟1,杨锁昌1,吕静2

(军械工程学院 1.导弹工程系;2弹药工程系,石家庄 050003)

摘要:舵机纵向修正能力随启控时刻的推后通常有先逐渐增大后逐渐减小的变化趋势。为提高纵向修正能力,从理论上分析了纵向修正能力变化趋势的形成原因,推导了基于摄动理论的纵向修正作用判别因子,并提出了以该判别因子为基础的纵向弹道修正改进方法。该方法通过在判别因子为正时设置常规的舵控相位,判别因子为负时设置与常规相反的舵控相位,使舵机在整个弹道上的修正作用不出现矛盾,从而扩展纵向修正时间、提高纵向修正能力。以装配固定鸭舵式二维修正引信的某型制导迫击炮弹为例进行了仿真,结果表明,该方法可将各射角的舵机纵向修正能力提高0～252%。通过蒙特卡洛模拟打靶验证了该方法应用于制导控制的可行性与有效性。

关键词:纵向弹道修正;摄动理论;固定鸭舵

随着现代战争的发展,为提高射击精度、减小附带毁伤,弹药制导化成为弹药发展的重要方向[1-2]。制导弹药执行机构的形式主要分为气动力执行机构[3-5]和直接力执行机构[6-7]。相对于直接力执行机构,气动力执行机构能够提供更大的修正能力并且能够实施连续修正,因此得到广泛应用。气动力执行机构的应用形式多样,其中固定鸭舵式二维修正引信被美国ATK公司提出并最早应用于155 mm榴弹和105 mm榴弹,称为精确制导组件(PGK),后又应用于120 mm迫击炮弹,称为迫击炮弹制导组件(MGK)。以固定鸭舵式二维修正引信代替常规引信实现弹药的制导化,具有容易实现、可靠性高、成本低的优点,成为弹药制导化方面的研究热点。

制导弹药纵向修正通常从进入弹道下降段后开始[3-5]。文献[3]指出进入弹道下降段开始纵向修正的原因是为了避免过早的增大弹体阻力,但是舵片偏转产生的升力一般远大于阻力,尤其是对于固定鸭舵式二维修正引信来说,启控与否对于弹体阻力几乎没有影响。文献[4]则指出对于以舵机为执行机构的尾翼稳定弹,在弹道顶点附近启控可取得最大修正能力,但是这里的最大修正能力对应的是常规的弹道修正方法,实际上常规的纵向弹道修正方法是有改进空间的。

论文以装配固定鸭舵式二维修正引信的某型制导迫击炮弹为例,仿真了纵向修正能力的变化趋势,分析了纵向修正能力变化趋势的形成原因,并提出了基于摄动理论的纵向弹道修正改进方法,最后通过蒙特卡洛模拟打靶验证了该方法应用于制导控制的可行性与有效性。

1纵向弹道修正的特点

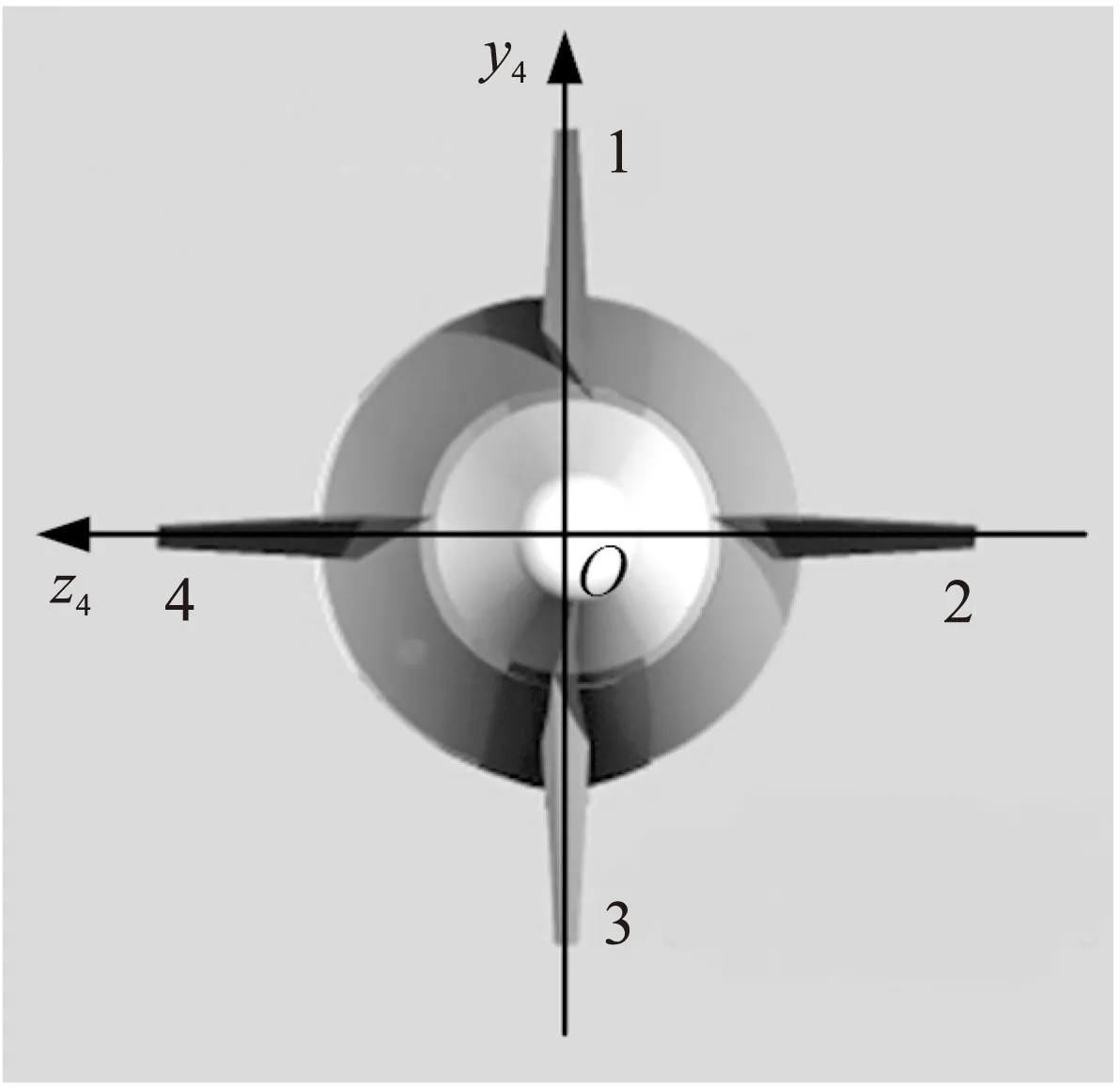
图1　固定鸭舵式二维修正引信示意图

固定鸭舵式二维修正引信示意图如图1所示,图中舵片1和舵片3称为一对差动舵,它们的舵偏方向相反,其作用是在弹体飞行过程中依靠舵片所受的气动力产生足够克服轴承摩擦的扭矩,使固定鸭舵式二维修正引信相对于弹体反向旋转。舵片2和舵片4称为一对修正舵,舵片2和舵片4的舵偏方向相同,修正舵稳定于某一角度时产生控制力,改变弹体姿态,达到修正弹道的目的。图1中Ox4y4z4为准弹体坐标系。

固定鸭舵式二维修正引信舵控相位φ的定义:修正舵位于准弹体坐标系水平面且舵片后缘向下时舵控相位为0;以0舵控相位为基准,修正舵向右旋转(从弹尾向弹顶看),舵控相位为正,当修正舵位于准弹体坐标系水平面且舵片后缘向上时舵控相位为π;以0舵控相位为基准,修正舵向左旋转,舵控相位为负,当修正舵位于准弹体坐标系水平面且舵片后缘向上时舵控相位为-π。

本节以装配固定鸭舵式二维修正引信的某型制导迫击炮弹为例,采用文献[8]中的低速滚转导弹运动方程组作为弹道仿真模型,仿真舵机纵向修正能力的变化趋势,仿真中气象采用标准气象条件,海拔设为200 m。迫击炮弹质量15 kg,尾翼稳定,初速设为330 m/s,固定鸭舵修正舵舵偏为6°,射角分别设为45°,55°,65°,80°,从某一启控时刻开始将修正舵稳定在舵控相位0,仿真得到的纵向修正能力曲线如图2所示。从图2可知,纵向修正能力随启控时刻的变化趋势通常不是单调的,有先逐渐增大后逐渐减小的变化趋势,在某一时刻取得最大值,射角不同时纵向修正能力取得最大值的时刻并不一致,射角分别为45°,55°,65°,80°时取得最大修正能力的时刻分别为5 s,9 s,17 s,23 s,最大值分别为388.5 m,237.4 m,180.7 m,152.8 m,而射角分别为45°,55°,65°,80°时弹道顶点时刻分别为17.1 s,19.6 s,21.6 s,23.5 s,可以看出,纵向修正能力取得最大值的时刻一般在弹道顶点时刻之前,射角越大,纵向修正能力取得最大值的时刻越靠近弹道顶点时刻。图2中tk为启控时刻,px为纵向修正能力。

图2　纵向修正能力曲线

纵向修正能力表现出上述变化趋势与舵机控制力的方向有关。舵控相位为0时,舵机控制力F在发射坐标系可分解为Fx和Fy,如图3所示,图3中Oxyz为发射坐标系。在弹道上升段,Fx为负,会减小弹丸水平分速度,起到了减小射程的作用;Fy为正,能够增加弹丸滞空时间,起到增大射程的作用。两者作用是相反的,Fx的减小射程作用可能大于Fy的增大射程作用,因此出现启控时刻早而修正能力变小的情况。在弹道下降段,Fx为正,起到增大射程的作用;Fy为正,也起到增大射程的作用,两者作用是相同的。因此,在弹道下降段,启控时刻越早修正能力越大。以80°射角弹道为例,从5 s开始启控,舵控相位设为0,舵机控制力在发射坐标系的投影如图4所示,图中,t为弹丸飞行时间。从图4可知,在飞行过程中,Fy始终为正,起到增大射程的作用;Fx开始时为负,逐渐变化为正,对射程起到的作用也相应从减小射程逐渐变化为增大射程。

图3　纵向修正时的受力分析

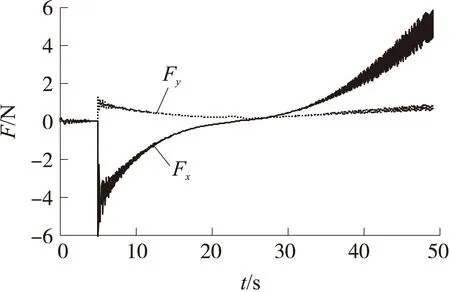
图4　舵机控制力在发射坐标系的投影

纵向修正能力随启控时刻的这种非单调的变化趋势广泛存在于以舵机为执行机构的各种弹道式制导弹药中,由于纵向修正能力在弹道顶点之前取得最大值,若启控时刻早反而会损失纵向修正能力,甚至得到相反的修正效果,因此一般将纵向修正启控时刻置于过弹道顶点后[3-5]。

常规的纵向弹道修正方法可归纳为以下2个方面的内容[4]。

①启控时刻。进入下降段后开始启控,即:

tk>tapex

(1)

式中:tk为启控时刻,tapex为弹道顶点时刻。

②舵控相位φ。由于进行纵向弹道修正的目的是使实际的射程接近目标射程,因此将射程偏差作为控制变量。舵控相位计算方法为

(2)

式中:ΔL为射程偏差(预测射程减目标射程)。

现有方法的主要问题在于:进入下降段开始进行纵向弹道修正,修正时间较短,修正能力必然受到影响。对于固定鸭舵式二维修正引信,受二维修正引信体积与弹体稳定性的制约,修正舵舵片面积与舵偏角度都受到限制,因此纵向修正能力偏小对固定鸭舵式二维修正引信的气象保障和瞄准精度提出很高的要求,成为制约固定鸭舵式二维修正引信射击精度与战场适应性的重要因素。

2纵向弹道修正方法改进及其工程应用分析

2.1纵向弹道修正方法改进

纵向修正能力先逐渐增大后逐渐减小的变化趋势表明:尽管仿真中舵控相位没有变化,但是纵向修正能力取得最大值之前,舵机对射程的修正作用与取得最大值之后舵机对射程的修正作用是相反的。本节通过理论分析得到舵机对射程的修正作用的变化规律,并以此为基础进行纵向弹道修正方法改进。

固定鸭舵式二维修正引信进行弹道修正时,修正舵被稳定在某一角度,假设从某一时刻开始启控并作用Δt时间,并假设舵机控制力不会造成弹丸失稳,修正舵产生的控制力可理解为:修正舵被稳定在某一角度时,相对于修正舵自由滚转时的空气动力增量。修正舵产生的控制力可表示为

(3)

式中:Fx4、Fy4、Fz4为修正舵产生的控制力在准弹体坐标系的各轴分量;ΔFRx4、ΔFRy4、ΔFRz4为弹丸修正舵被稳定在某一角度时,相对于修正舵自由滚转时的空气动力增量在准弹体坐标系的各轴分量。

在进行纵向修正时,ΔFRz4≈0,另外空气阻力增量远小于法向力增量,也可以认为是0,即ΔFRx4≈0,则式(3)可改写为

(4)

准弹体坐标系到发射坐标系的转换矩阵为

(5)

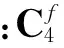
舵机控制力在发射系的投影可表示为

(6)

式中:Fx,Fy,Fz为舵机控制力在发射坐标系的各轴分量。

由于ψ较小,cosψ≈1,sinψ≈0,式(6)可改写为

(7)

设Δt足够短,在Δt时间内Fy4保持不变,则Δt时间后,弹丸将获得速度增量与位置增量。

速度增量可表示为

(8)

式中:Δvx,Δvy,Δvz为舵机作用Δt时间后弹丸获得的速度增量在发射系的各轴分量;m为弹丸质量。

位置增量可表示为

(9)

式中:Δx,Δy,Δz为舵机作用Δt时间后弹丸获得的位置增量在发射系的各轴分量。

弹丸获得的速度与位置增量最终形成对弹丸射程的影响。根据摄动理论[9],弹丸的速度与位置增量对射程的影响可表示为

(10)

式中:L为射程函数;∂L/∂x,∂L/∂y,∂L/∂vx,∂L/∂vy分别为射程对水平位置、垂直位置、水平分速度和垂直分速度的敏感因子;δL为舵机作用Δt时间取得的射程修正量。

将式(8)和式(9)代入式(10)可得:

(11)

式中:(Δt)2为二阶小量,可忽略。则式(11)可改写为

(12)

式中:δL的正负表明了舵机对射程的修正作用,δL为正时表示远修作用,δL为负时表示近修作用。

定义变量a为判别因子,并令:

(13)

式(12)中Fy4的正负与舵控相位是相对应的,因此δL的正负与舵控相位和a的值存在如下关系:

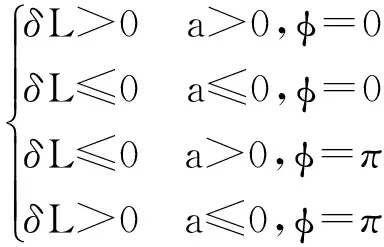
(14)

从式(14)可知,舵机控制在某一时刻的射程修正量的正负与a的值和舵控相位有关,其中,a的值是弹道本身的性质,是不可控的,但是舵控相位是可控的,因此,可以根据a的值,对舵控相位进行转换,从而控制舵机在整个弹道段对射程的修正作用。

基于以上分析,提出对纵向弹道修正方法的改进方案:

①启控时刻tk。启控时刻尽可能提前,启控时刻设为可设置的最早启控时刻,最早启控时刻根据制导系统初始化时间、收星定位时间、弹体稳定性条件等确定。

tk>t0

(15)

式中:t0为可设置的最早启控时刻。

②舵控相位。舵控相位由射程偏差与判别因子的值共同确定。即:

(16)

改进的舵机纵向弹道修正方法的优势在于纵向弹道修正时间不再局限于弹道下降段,只要制导系统准备完毕并且满足稳定性条件就可以开始纵向弹道修正,而纵向弹道修正得以扩展到弹道上升段的关键是根据判别因子a的值对舵机在某一时刻的射程修正量的正负进行判断,a为正时设置常规的舵控相位,a为负时设置与常规相反的舵控相位。由于a是基于摄动理论得到的,所以称该方法为基于摄动理论的纵向弹道修正改进方法。

采用舵机纵向弹道修正改进方法,仿真的45°,55°,65°,80°各射角纵向修正能力如图5所示。从图5可知,各射角的纵向修正能力随启控时刻的变化趋势都是单调的,这说明采用基于摄动理论的判别因子可准确判断舵机控制在某一时刻射程修正量的正负。射角为45°,55°,65°,80°时取得最大修正能力的启控时刻都是5s,最大值分别为388.5m,353.1m,473.9m,538.0m,纵向修正能力相对于常规方法分别提升了0,29%,162%,252%。

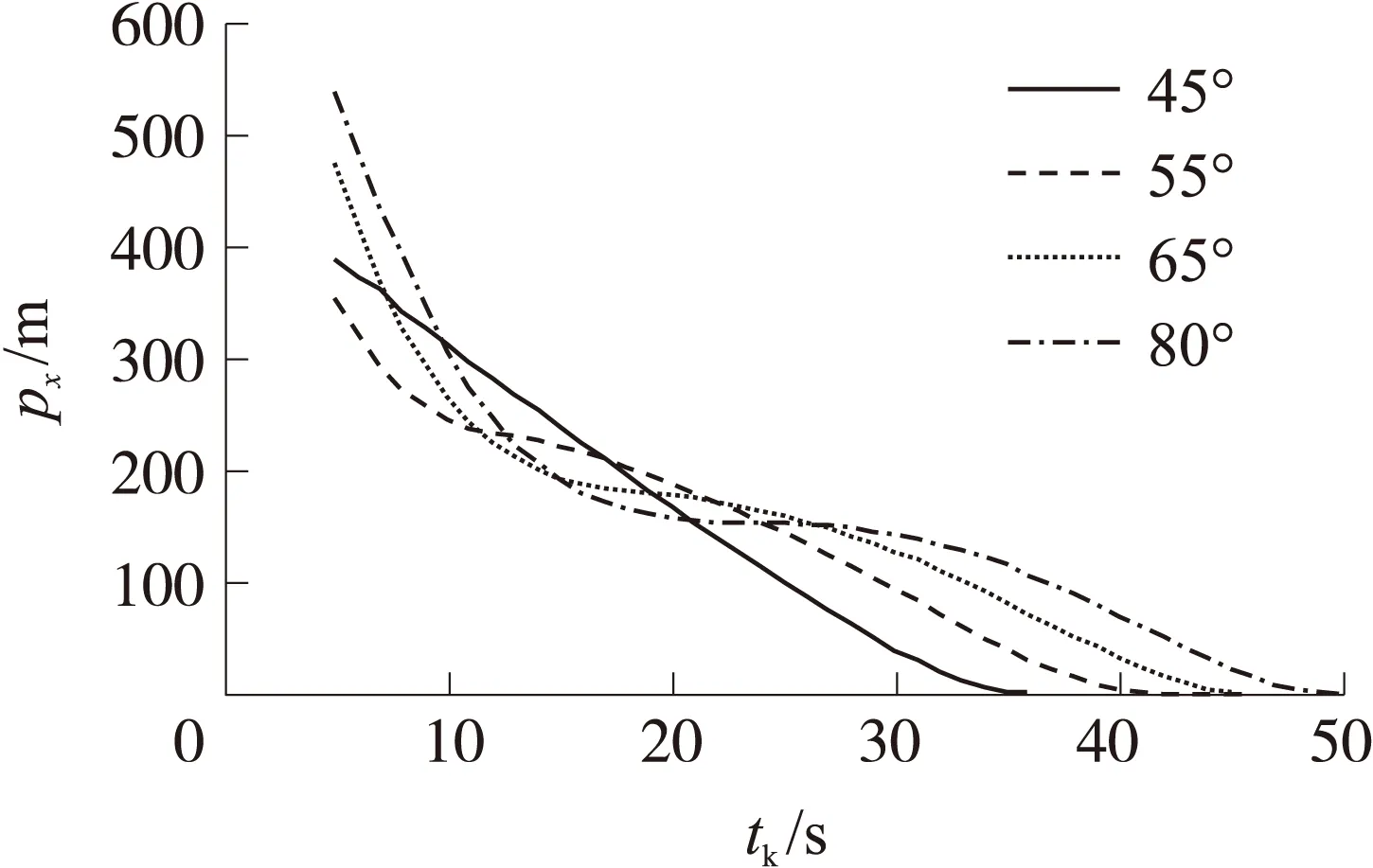
图5　改进方法的修正能力曲线

2.2工程应用性分析

式(12)中∂L/∂vx和∂L/∂vy可以采用地面计算机解算,并在射前装定到弹载计算机,弹载计算机根据弹丸位置插值出相应的∂L/∂vx和∂L/∂vy值,而俯仰角φ可通过弹上陀螺测得,如果是不装配陀螺的GPS制导弹药,可用弹道倾角θ代替俯仰角进行计算,因此,该方法在工程上是易于实现的。

3仿真计算分析

如前文所述,采用基于摄动理论的纵向弹道修正改进方法可以扩展纵向弹道修正时间,大幅提高舵机纵向修正能力。而纵向修正能力的提高理论上有利于提高制导迫击炮弹的射击精度。本节通过蒙特卡洛模拟打靶验证所提出的纵向弹道修正改进方法应用于制导控制的可行性与有效性。

采用摄动制导[9]作为迫击炮弹的制导方法。摄动制导的应用需要射前装定∂L/∂vx和∂L/∂vy等射程对高程、水平分速度和垂直分速度的敏感因子,基于摄动理论的纵向弹道修正改进方法正好可以利用其中的∂L/∂vx和∂L/∂vy敏感因子,不需另行计算与装定,这是采用摄动制导作为制导方法的一个优势。

模拟打靶射程为2 000m,射角为78.86°,弹丸初速为330m/s,气象采用标准气象条件,海拔设为200m。在模拟打靶中,假设制导迫击炮弹以GPS为制导工具,GPS定位误差(1个标准差)取值为:水平定位误差8m,垂直定位误差12m,水平定速误差0.3m/s,垂直定速误差0.4m/s。模拟打靶中各项扰动(1个标准差)取值为:轴向力系数偏差1%,初速偏差2m/s,质量偏差250g,射角偏差0.3°,射向偏差0.3°,纵风1.5m/s,横风1.5m/s。

1)仿真计算1。制导迫击炮弹无控状态下模拟打靶。打靶结果如图6(a)所示,图中，L为射程,H为横偏。从图6(a)可知,迫击炮弹无控条件下的落点偏差较大,纵向落点偏差范围为-382.4～324.8m,横向落点偏差范围为-194.8～180.3m,经统计,射程中间误差为77.2m,横偏中间偏差为48.3m。

2)仿真计算2。制导迫击炮弹有控状态下模拟打靶。为排除横向控制的影响,将横向设为无控。舵机纵向弹道修正方法见式(1)和式(2)。模拟打靶结果见图6(b),从图6(b)可知,大部分弹道的射程偏差得到了有效修正,但是受限于纵向修正能力,一些比较大的射程偏差未得到完全修正,修正后的纵向落点偏差范围为-206.7～146.5m,横向落点偏差范围为-193.1～190.7m,经统计,射程中间偏差为18.8m,横偏中间偏差为48.7m。

3)仿真计算3。制导迫击炮弹有控状态下模拟打靶。横向设为无控。纵向弹道修正方法见式(15)和式(16)。根据现有的技术水平,制导系统能够在5s内完成初始化、收星定位等准备工作,并且5s后满足稳定性要求,因此将启控时刻设为5s。由于仿真中制导迫击炮弹以GPS为制导工具,因此采用弹道倾角代替俯仰角计算判别因子的值。打靶结果如图6(c)所示,从图6(c)可知,纵向落点偏差范围为-18.8～13.2m,横向落点偏差范围为-197.5～179.4m,经统计,射程中间误差为3.7m,横偏中间偏差为48.5m。从模拟打靶结果可以看出,得益于修正能力提升,所有弹道的射程偏差都得到了有效修正,与此同时,没有影响横向的落点散布。该结果证明了本文提出的基于摄动理论的纵向弹道修正改进方法应用于制导控制的可行性与有效性。

图6　落点散布

4结束语

本文以装配固定鸭舵式二维修正引信的某型制导迫击炮弹为例,分析了纵向修正能力变化趋势及其形成原因,推导了基于摄动理论的纵向修正作用判别因子,并提出了以该判别因子为基础的纵向弹道修正改进方法。判别因子为正时, 设置常规的舵控相位;判别因子为负时,设置与常规相反的舵控相位。从而,对舵机在整个弹道上的射程修正作用进行有效控制。应用该方法可以将纵向弹道修正时间扩展到上升段,并大幅提高舵机的纵向修正能力。仿真表明,通过该方法可以将各射角的舵机纵向修正能力提高0～252%。蒙特卡洛模拟打靶结果显示,采用传统控制方法可将射程中间偏差从77.2m减小到18.8m,而采用提出的纵向弹道修正改进方法后,射程中间偏差减小到3.7m,该结果证明了论文提出的纵向弹道修正改进方法应用于制导控制的可行性与有效性。

参考文献

[1]BIASS E H,BRAYBROOK R.Guided mortar bombs[J].Armada International,2002,26(6):56-57.

[2]GANDER T J.Mortar ammunition update[J].Armada International,2003,27(2):18-20.

[3]ROGERS J,COSTELLO M.Design of a roll stabilized mortar projectile with reciprocating canards[J].Journal of Guidance,Control,and Dynamics,2010,33(4):1 026-1 034.

[4]FRESCONI F.Guidance and control of a projectile with reduced sensor and actuator requirements[J].Journal of Guidance,Control,and Dynamics,2011,34(6):1 757-17 66.

[5]THEODOULIS S,GASSMANN V,WERNERT P.Guidance and control design for a class of spin-stabilized fin-controlled projectiles[J].Journal of Guidance,Control,and Dynamics,2013,36(2):517-531.

[6]PAVIC M,PAVKOVIC B,MANDIC S,et al.Pulse-frequency modulated guidance laws for a mortar missile with a pulse jet control mechanism[J].Aeronautical Journal,2015,119(1213):389-405.

[7]GAO Min,ZHANG Yong-wei,YANG Suo-chang.Trajectory correction capability modeling of the guided projectile with impulse thrusters[J].Engineering Letters,2016,24(1):11-18.

[8]钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2000:28-77.

QIAN Xing-fang,LIN Rui-xiong,ZHAO Ya-nan.Missile dynamics of flight[M].Beijing:Beijing Institute of Technology Press,2000:28-77.(in Chinese)

[9]陈世年.控制系统设计[M].北京:宇航出版社,1996:161-175.

CHEN Shi-nian.Control system design[M].Beijing:China Astronautic Publishing House,1996:161-175.(in Chinese)

Improvement of Longitudinal Trajectory-correction Method Based on Perturbation Theory

GAO Min1,ZHANG Yong-wei1,YANG Suo-chang1,LV Jing2

(1.Missile Engineering Department;2.Ammunition Engineering Department,Ordnance Engineering College,Shijiazhuang 050003,China)

Abstract:The longitudinal trajectory-correction capability usually varies in a non-monotonic way with the increase of the control start time.The reason of the change trend of the longitudinal trajectory correction capability was analyzed theoretically,and the discriminant function of trajectory-correction based on perturbation theory was deduced.The optimized method of canards control in longitudinal plane was put forward based on the discriminant function of trajectory correction.The conventional canards control phase was set when the discriminant function of trajectory correction was positive;the optimized canards control phase was set when the discriminant function of trajectory correction was negative.This method can make sure that the trajectory correction direction is same,so the longitudinal trajectory correction capability is increased greatly.The simulation of one guided mortar projectile with fixed canards was carried out.The simulation result shows that this method can increase the longitudinal trajectory-correction capability with different elevation angles by 0-252%.The effectiveness and adaptability of this method on application was testified by Monte-Carlo simulation.

Key words:longitudinal trajectory correction;perturbation theory;fixed canards

收稿日期:2016-01-23

作者简介:高敏(1963- ),男,教授,博士,博士生导师,研究方向为弹箭智能化与信息化。E-mail:gaomin1103@yeah.net。

中图分类号:TG412

文献标识码:A

文章编号:1004-499X(2016)02-0029-06