T形钢管再生混凝土柱抗震性能的有限元非线性分析

2016-07-15龚玉云李文芳

长江大学学报(自科版) 2016年16期

关键词：抗震性能有限元分析影响因素

龚玉云，李文芳

(长江大学城市建设学院，湖北荆州 434023)

T形钢管再生混凝土柱抗震性能的有限元非线性分析

龚玉云，李文芳

(长江大学城市建设学院，湖北荆州 434023)

[摘要]为研究T形钢管再生混凝土柱在低周反复荷载作用下的抗震性能，在选择合适材料本构关系的基础上，采用有限元软件ABAQUS，模拟得到了3根不同再生骨料取代率下T形钢管再生混凝土柱的荷载-位移曲线，通过滞回曲线分析了不同替代率对试件水平承载力、延性和耗能能力的影响，并将轴压比、含钢率和钢材强度作为变化参数，用建立的有限元模型对T形钢管再生混凝土柱的抗震性能进行非线性分析。研究结果表明，不同取代率对试件的滞回曲线影响不大，所有柱的滞回曲线都非常饱满，说明T形钢管再生混凝土柱具有良好的抗震性能；轴压比对试件骨架曲线影响较大，随着轴压比的增大，试件水平承载力逐渐减小，且下降幅度变大，表现出更差的延性；含钢率对试件初始刚度和抗震性能影响很大，含钢率越大，试件初始刚度也越大，水平承载力和抗震性能也越好；钢材强度对试件的初始刚度影响不大，强度越大，试件的水平承载力越高，抗震性能越好；研究成果可供异性截面钢管再生混凝土结构的推广使用提供参考。

[关键词]钢管再生混凝土；T形截面柱；有限元分析；影响因素；抗震性能

异形截面钢管混凝土结构是指将钢管制作成异性截面后填充混凝土形成的新型组合结构。异形截面柱能够避免房间出现棱角、利于室内空间布局和增加使用面积。再生混凝土是指将废弃混凝土破碎成再生骨料，重新拌制成混凝土继续使用。由于再生混凝土的力学性能比普通混凝土要差，将再生混凝土填充至T形钢管中即可形成钢管混凝土柱，能否将该结构用于抗震设防区的高层及超高层结构中，则需要对其进行深入的研究以获取其抗震性能指标，这无疑具有十分重要的现实意义[1，2]。

在钢管混凝土框架结构中，框架柱是其重要的组成部分和关键部位。现阶段，对异性钢管混凝土结构的研究较少。黎志军等[3]、陈之毅等[4]、周海军等[5]、王玉银等[6]、林震宇等[7]对T形、L形钢管混凝土柱的轴压力学性能和抗震性能进行了试验研究，并提出了相应承载力计算公式。张继承等[8，9]、曹兵等[10]对异形截面钢管混凝土柱抗震性能进行了非线性有限元分析，除此之外，尚未检索到有关T形截面钢管再生混凝土柱有限元分析的文献与报道。

因此，笔者拟在选择合适本构关系的基础上，建立T形截面钢管再生混凝土柱模型，分析再生骨料替代率为0%、50%、100%下T形截面钢管再生混凝土柱的抗震性能。再基于建立的模型，改变轴压比、含钢率和钢材强度等参数，考察不同参数对柱抗震性能的影响和规律，以期为异性截面钢管再生混凝土结构的推广使用及试验设计提供参考依据。

1T形截面柱尺寸及材料性质

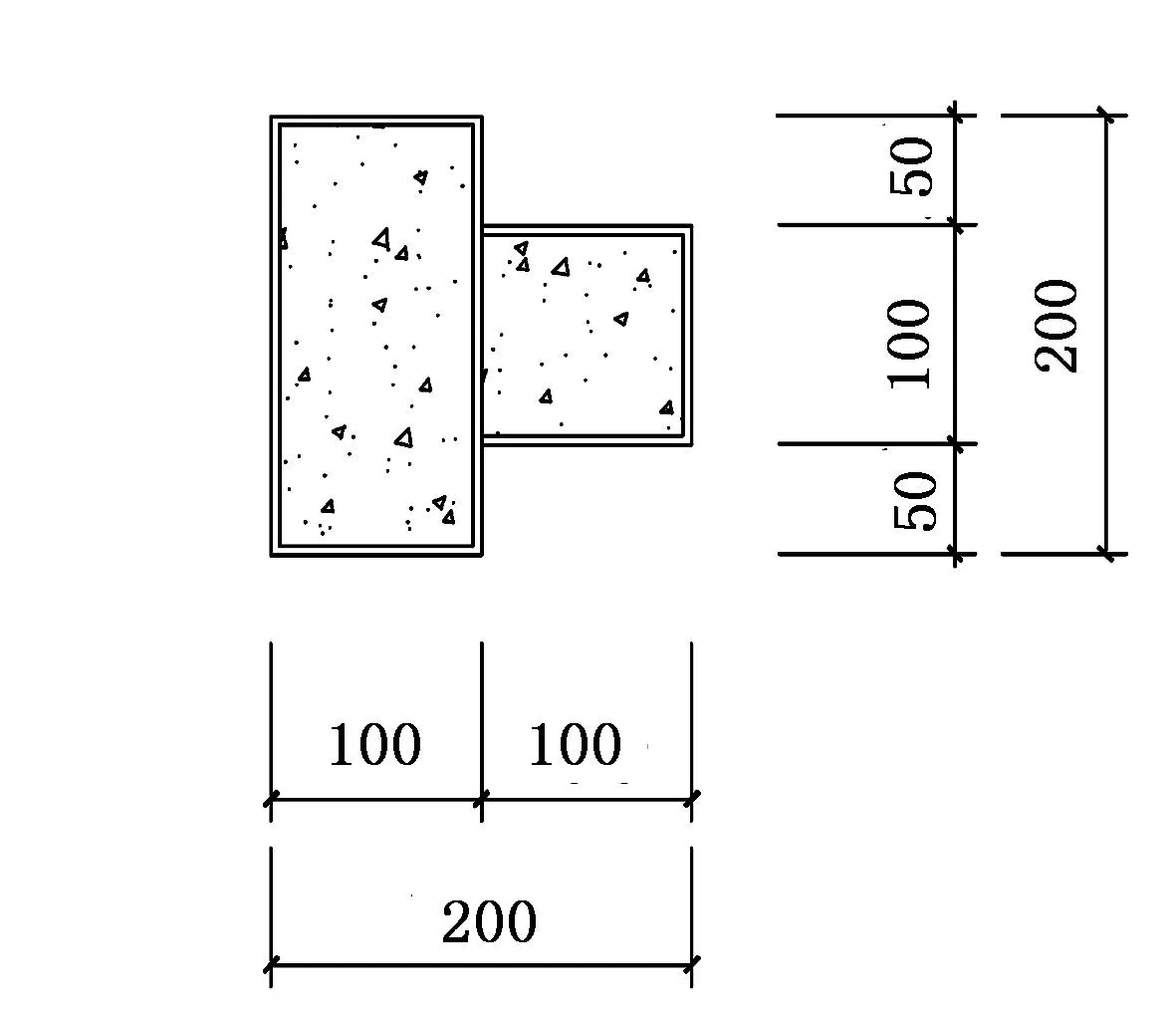
图1　T形截面柱尺寸示意图

采用有限元软件模拟时，需先确定模型尺寸和材料性质。T形截面钢管混凝土柱的尺寸和钢管性质见文献[11]，钢管内核心再生混凝土的性质见文献[12]。T形截面柱用截面尺寸200mm×100mm×4mm矩形钢管和冷弯折成截面尺寸100mm×100mm×4mm的U形钢板组合而成，柱的高度为1000mm，设计轴压比为0.4，截面尺寸见图1。钢管的屈服强度、抗拉强度及弹性模量的实测值为273.8MPa、387.0 MPa及201GPa。混凝土的材料性质见表1。

表1　再生混凝土材料性质

2有限元模型建立

2.1本构关系

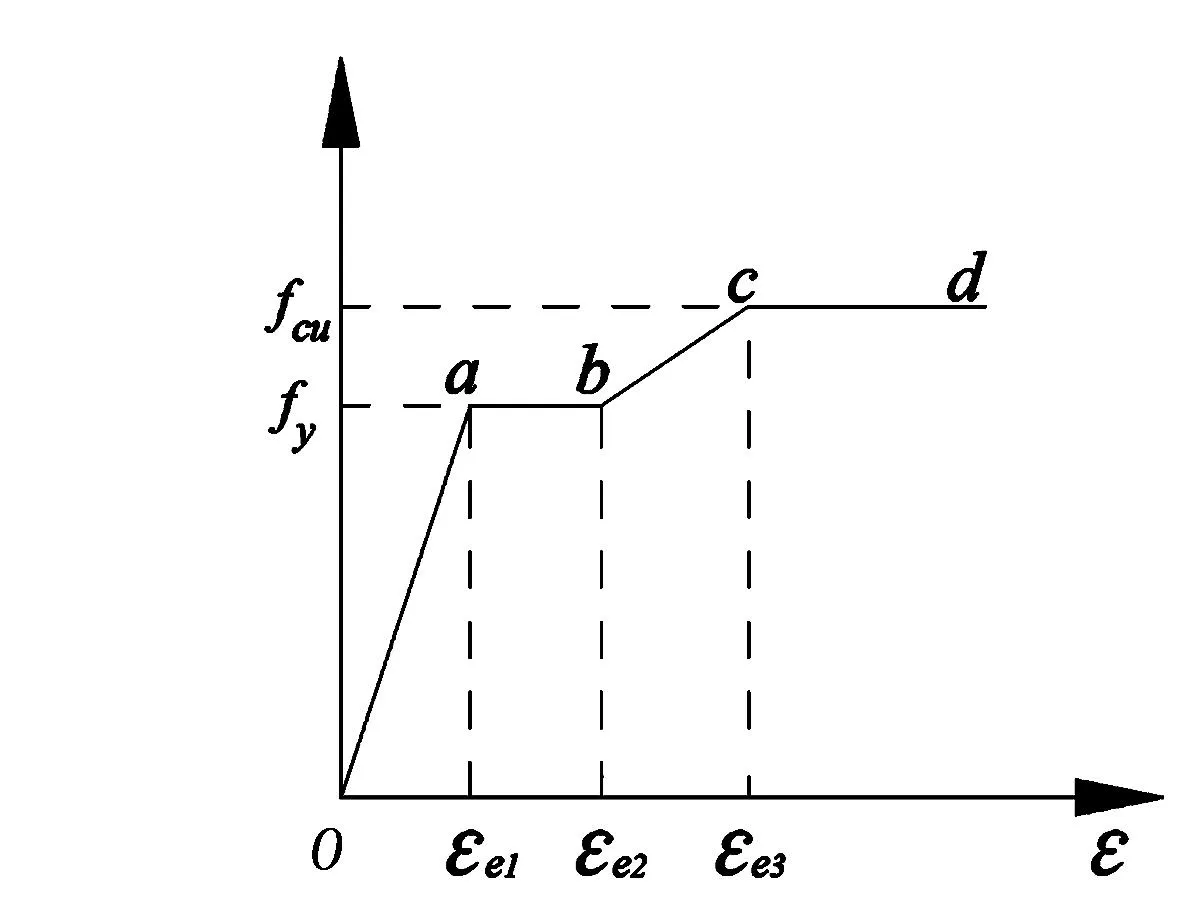
图2　二次塑流模型

1)钢材的本构模型二次塑流模型被广泛用于钢管混凝土结构中钢材的本构关系中，因为它不仅能考虑到钢材的强化，还能较为真实可靠的反应出材料特性：

(1)式中，fy为钢材的屈服强度；fcu为钢材的极限抗压强度；E为弹性模量；E′为强化模量；εe1为弹性极限应变，εe2=10εe1，εe3=100εe1=10εe1。

钢材适用于Von Mises屈服准则，该准则被普遍用于金属材料，二次塑流模型示意见图2。

图3　有限元模型示意图

2)再生混凝土的本构模型ABAQUS软件中提供了混凝土塑性损伤模型，该模型可用于循环加载。混凝土在加载过程中发生的损伤可用非关联硬化塑性和各项同性损伤弹性相结合的方式予以描述，且收敛效果较好，混凝土的本构关系采用文献[14]中使用的本构关系。

2.2单元选择和网格划分

1)单元选择在有限元分析中，实体单元是使用最广泛的部件，它可以通过其中一个平面与其他单元连接，以此来构造出任意模型。再生混凝土采用C3D8R单元，钢管采用S4R单元。这两类单元均是线性缩减积分单元，具有以下优点：①该积分单元的均匀应变公式比完全积分单元更加精准，故其得到的位移计算结构也更为准确；②能够在扭曲变形很大的情况下，也能保证分析精度；③弯曲荷载作用下，剪切自锁现象极少发生。

2)网格划分有限元法的本质就是将无线自由度转化为有限自由度，将连续模型转换成离散模型分析以得到近似结果。网格过大或过小都不合适，过大会导致计算结果不准确，过小增加计算负担，延长计算时间。划分网格时，对T形钢管混凝土柱采用结构化网格划分技术，有限元模型见图3。

2.3界面模型

在处理钢管与混凝土界面时，一般有2种方式可供参考：①假设钢管与混凝土共同受力并产生变形，也就是忽略了钢管与混凝土之间的黏结滑移；②考虑钢管与混凝土之间的黏结滑移问题，即接触问题。文献[13]的研究结果表明，未考虑黏结滑移情况下的计算结果更加接近于试验实测结果。因此，笔者不考虑钢管与混凝土之间的黏结滑移问题，即假设钢管与混凝土协同变形。

2.4边界条件及加载方式

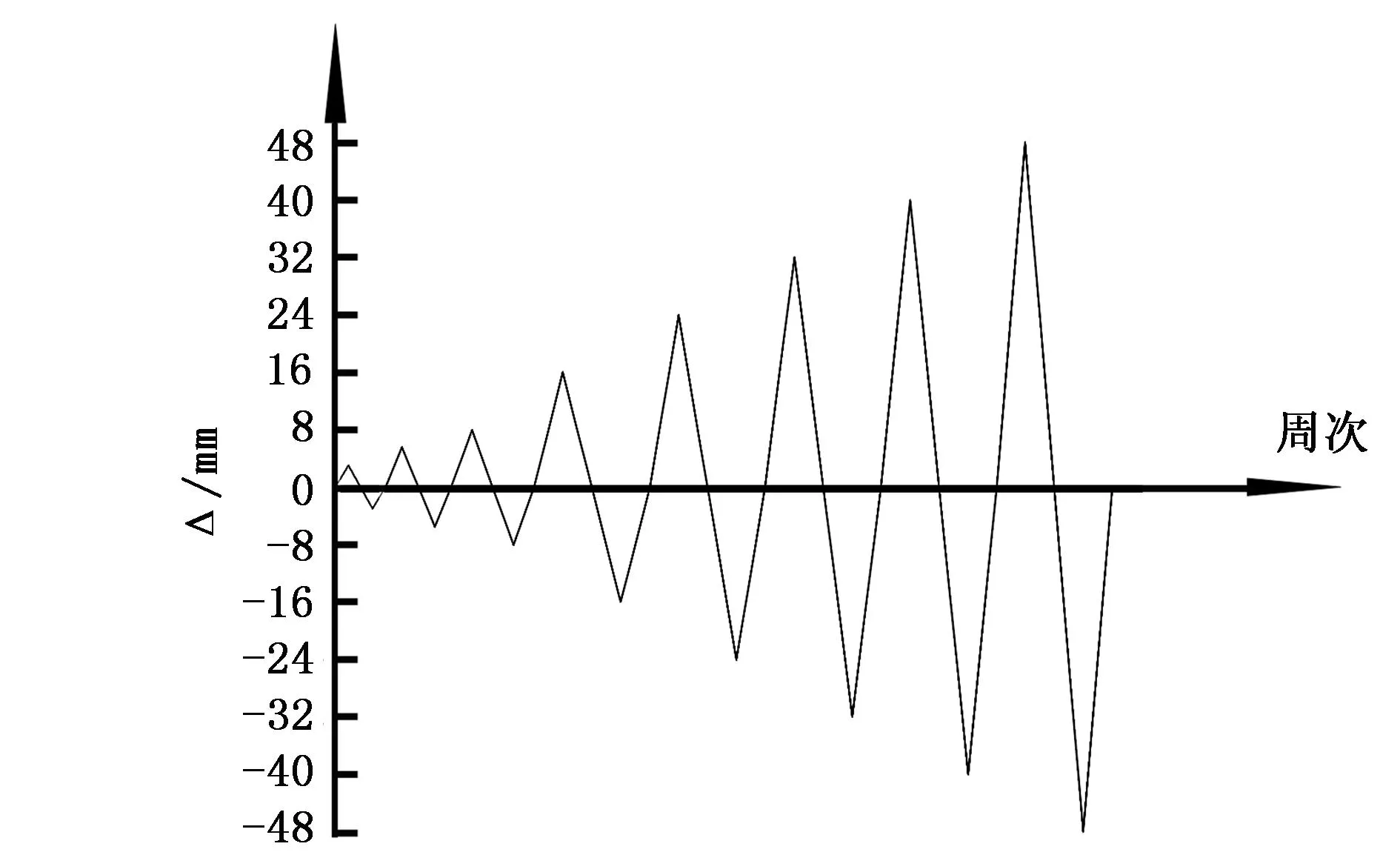
图4　加载示意图

1)边界条件笔者建立的模型的边界条件为在柱底端固定所有自由度，柱顶施加集中轴向荷载，顶部再施加水平位移荷载。为了更好模拟试件在实际中的受力情形，加载方式采用多步骤分析法。一共分为3分析步：第1分析步，在模型上施加位移约束；第2分析步，在柱顶施加均布轴向荷载，之后的加载中保持轴力不变；第3分析步，在加载点施加位移荷载。

2)加载方式有限元计算时，采用位移加载时，计算结果易收敛。故加载采用位移控制加载，加载示意图见图4。

3有限元模型结果

3.1滞回曲线

通过有限元计算试件的滞回曲线(见图5)，其中，P表示水平柱顶荷载，Δ表示水平柱顶位移。

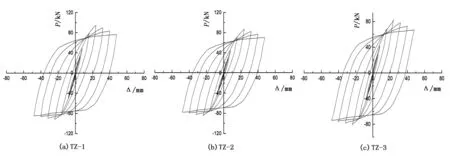
图5　各试件滞回曲线

由图5可知，滞回曲线具有以下特征：①弹性工作阶段，试件的滞回曲线基本重合为一条直线，初始刚度保持不变。继续加载，荷载得到了提高。超过极限荷载后，承载力开始逐步降低。滞回曲线倒向位移轴，反应出随着加载的进行，损伤进一步加大。滞回环逐渐变得饱满，说明耗能能力逐步加大。②所有试件的滞回曲线十分饱满，无捏缩现象，表现出较好的稳定性。③试件TZ-2、TZ-3与试件TZ-1的取代率不同，但滞回曲线的形状与之差别不大，基本相同，表明取代率对T形钢管再生混凝土柱的滞回曲线影响不大。

3.2骨架曲线

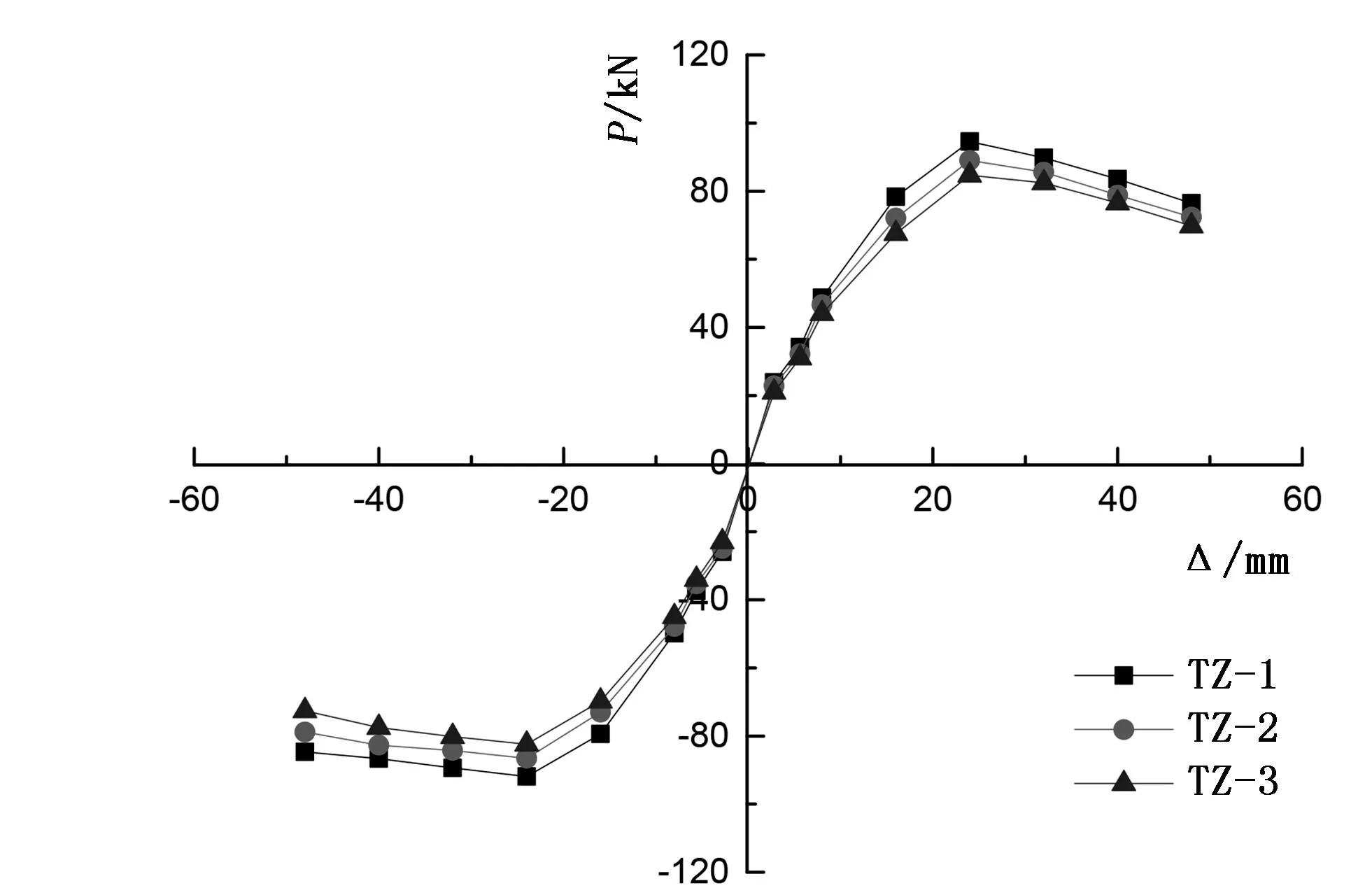
图6　骨架曲线

将各试件的滞回曲线上每级循环峰值点提取出来，绘制于同一张图中，得到的骨架曲线(见图6)。从图6可知：①3个试件的骨架曲线大体相同，比较完整，都有上升段、极限段和下降段。其骨架曲线的后期变形能力强，延性较好。这主要是因为钢管和混凝土的共同作用，核心再生混凝土的支撑延缓了钢管的鼓曲变形，而钢管的包裹又使得核心再生混凝土的抗压强度和变形能力得到提高。这2种材料互相作用，保证了材料的性能得到充分发挥。②试件TZ-1、TZ-2、TZ-3的变化参数为再生骨料取代率，3个试件的骨架曲线弹性段基本重合，说明取代率对T形钢管再生混凝土柱的初始阶段弹性刚度基本无影响；极限荷载过后，3个试件的骨架曲线有所分离，但分离程度不大。这是由于取代率不一样，再生混凝土的初始损伤不一样，但这种损伤在加载前期因为钢管对混凝土的约束作用而基本不表现出现。但随着加载的持续，损伤程度逐步加大，故造成试件后期下降段的刚度有所不同。

3.3延性和耗能能力

采用能量等值法求出各试件的屈服位移，并采用等效粘滞阻尼系数来评估各试件的耗能能力。表2列出了各试件的相关抗震性能指标。

表2　各试件延性及耗能指标

从表2可知，随着再生骨料取代率的提高，试件所能达到的极限荷载值逐渐降低。所有试件的位移延性系数在3.18～3.36，等效粘滞阻尼系数在0.46～0.48。说明再生骨料取代率对试件的延性和耗能能力影响甚微，而普通混凝土柱的等效粘滞阻尼系数在0.1～0.2，证实了T形钢管混凝土柱具有较好的耗能能力。

4影响因素分析

数值计算的好处是可以方便快捷的计算，消除了试验条件的限制。为了探究其余材料参数对T形钢管再生混凝土柱抗震性能的影响，基于已建立的有限元模型，将轴压比、含钢率和钢材强度作为变化参数，获得各参数下试件的骨架曲线，获得相关参数对试件骨架曲线影响的规律。

4.1轴压比的影响

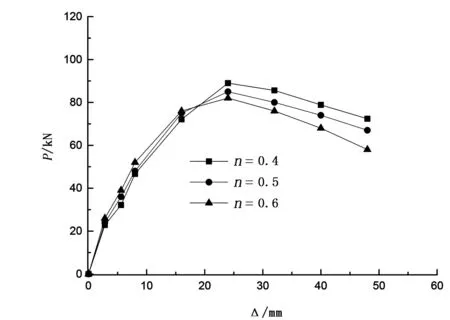
图7　不同轴压比下T形柱骨架曲线

以取代率50%的试件TZ-2为研究对象，该柱试验轴压比n=0.4，再对轴压比n=0.5、0.6时进行分析。图7为试件在不同轴压比利用有限元计算得到的骨架曲线，仅取正向段的骨架曲线为研究对方。

从图7可知，轴压比对荷载-位移骨架曲线的形状影响较大。加载初期，轴压比大的试件承载力高于低轴压比试件，但程度不明显，也就是说轴压比在0.4～0.6时，对试件的初始刚度影响不明显。在所选轴压比变化幅度内，轴压比越大，所能达到的极限荷载反而越低。极限荷载过后，轴压比越大，试件的骨架曲线下降趋势越陡，直到结构失效。这是由于达到极限荷载后，轴压比越大，对应的轴压力越大，二阶效应也越大，造成T形柱损伤加大，故承载力衰减速度加快。

4.2含钢率的影响

基于有限元模型，对钢管壁厚t=5、6mm，利用有限元软件计算的骨架曲线(见图8)。

从图8可以看出，随着钢管壁厚的增加，试件的初始刚度也随着增加，说明含钢率对试件的初始刚度起到了有益作用。钢管壁厚大的试件在不同位移下的水平承载力都比钢管壁厚小的要大，钢管壁厚越大，骨架曲线与位移轴包围的面积也更大，耗能能力也越好。

4.3钢材强度的影响

工程中常见的钢材等级有Q235、Q345和Q390，笔者选取这3种钢材等级进行分析。以试件TZ-2为研究对象，基于已有的有限元模型，替换钢材屈服强度fy进行计算，得到的不同钢材强度等级下T形柱的骨架曲线见图9。

图8　不同含钢率下T形柱骨架曲线　　　　图9　不同钢材屈服强度下T形柱骨架曲线

从图9可知，随着钢材强度的增加，T形柱的初始刚度几乎不变化，说明钢材屈服强度对T形钢管再生混凝土柱的初始刚度并不会产生明显影响。钢材屈服强度越大，试件的极限荷载越大。骨架曲线与位移轴包围的面积表示试件在加载过程中所耗散的能量，钢材屈服强度越大，试件的耗能能力越好，下降段更平缓，骨架曲线水平段大大增加，延性性能有所增加，抗震性能更优。

通过对含钢率和钢材强度影响的分析可知，若结构上钢材的屈服强度和钢管壁厚增加，则结构的承载力和耗能能力会得到极大提升。首先，钢材强度和含钢率可以使得结构水平承载力得到提升，另外，钢材强度和含钢率越高，其对管内核心再生混凝土的约束也会加大，这样对混凝土的强度和延性有益，证实了T形钢管再生混凝土柱可在抗震设防区的建筑结构上使用。

5结论

在选择合适材料本构关系的基础上，采用有限元软件ABAQUS，模拟得到了3根不同再生骨料取代率下T形钢管再生混凝土柱的荷载-位移曲线。并基于建立的有限元模型，分析了轴压比、含钢率和钢材强度这3个因素对试件抗震性能的影响，可以得到以下结论：

1)利用有限元软件计算得到的所有柱的滞回曲线都非常饱满，说明T形钢管再生混凝土柱具有良好的抗震性能，而不同再生骨料取代率对试件的滞回曲线影响不大。

2)在其他条件相同时，在所选择的参数取值范围内，轴压比和钢材强度对试件的初始刚度影响不大，但含钢率对试件初始刚度影响较大。

3)随着轴压比的增大，试件水平承载力逐渐减小，且下降幅度变大，表现出更差的延性；分别提高含钢率和钢材强度，试件的水平承载力也会得到越高，抗震性能也会更好。

4)T形钢管再生混凝土结构具有优异的抗震性能，可以在抗震设防区推广使用。

[参考文献]

[1]许成祥，杨炳，赵斌，等. 外包钢加固震损钢管混凝土柱的抗震性能试验[J]. 广西大学学报(自然科学版)，2015，40(4): 821～830.

[2] 杨炳，许成祥，赵斌，等. 钢套法加固方钢管混凝土柱抗震性能试验研究[J]. 广西大学学报(自然科学版)，2015，40(5): 29～37.

[3] 黎志军，蔡健，谭哲东，等. 带约束拉杆异性钢管混凝土柱力学性能的试验研究[J]. 工程力学，2001，16(2)：124～129.

[4] 陈之毅. 矩形钢管混凝土结构施工工艺及异形柱承载力的研究[D]. 上海：同济大学，2003.

[5] 周海军. 反复荷载作用下L形钢管混凝土柱力学性能研究[D]. 上海：同济大学，2003.