基于Python语言的大学物理实验数据处理方法研究

钟志强

(鞍山师范学院 物理科学与技术学院,辽宁 鞍山 114007)



基于Python语言的大学物理实验数据处理方法研究

钟志强

(鞍山师范学院 物理科学与技术学院,辽宁 鞍山 114007)

摘要以大学物理实验中的单摆周期测量、螺线管霍尔效应和单摆简谐运动为例，探讨了Python语言在随机误差分布规律、数据回归分析和机械运动模拟中的应用方法.研究表明，Python处理实验数据的方法简便灵活，表征数据图形直观明了，适宜推广使用.

关键词Python；大学物理实验；数据分析

目前,应用计算机软件分析实验数据已成为大学物理实验教学中的一个重要环节，最具代表性的软件是MATLAB(Matrix Laboratory,矩阵实验室).但与MATLAB相比，Python是一门更易学、更严谨的程序设计语言，最重要的是其开源和免费.Python是一种面向对象、支持动态语义、内置高级数据结构、语法简洁优美、易于扩展的解释型脚本语言(script language)[1].Python扩展库中的NumPy 相当于Matlab，它提供了矩阵、线性代数、傅里叶变换等的解决方法，还包含Fortran 代码集、C++代码集.MATLAB主要专注于工程和科学计算，然而即便是在计算领域也会遇到文件操作、网络通信、界面操作与管理等程序语言要求，这一点MATLAB也不如Python出色[2].此外，对于同样是开源、免费的R软件而言，其应用核心领域为数理统计分析，尽管在机器学习等领域也颇有建树，但其运行效率和在虚拟实验等应用范围上的表现仍不及Python.

虽然Python语言应用广泛，但在大学物理实验中应用并不多见[3].国内的实验分析仍以MATLAB为主[4,5].为此，我们对物理实验教材中的经典实验进行分析,并省略实验的基本原理和实验公式的推导过程，突出表现Python语言数据分析统计、绘图和仿真应用的基本过程.

1单摆周期随机误差分布

1.1数据的采集

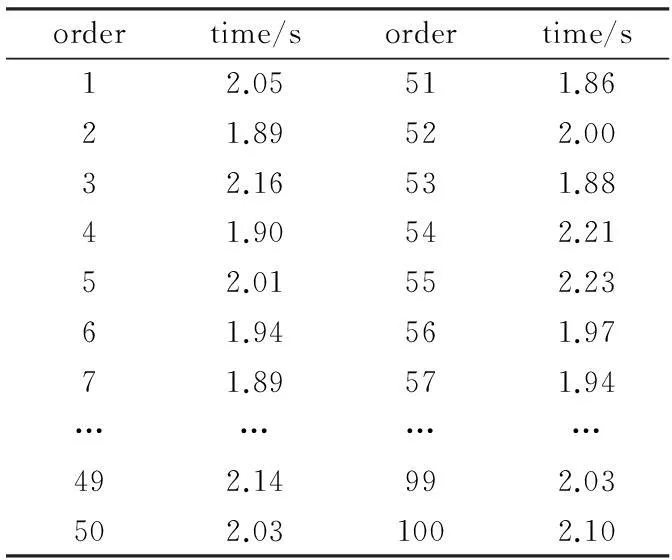
表1　单摆摆动周期表(局部)

参考大学物理实验教材(一、力学及热学部分)[6]，本实验是通过光电门，记录单摆周期T实验，目标是通过采集样本、绘制样本分布函数和密度函数、对样本进行参数估计及假设检验等环节加深学生对正态分布的理解.记录的次序(order)和对应时间(time(s)) 见表1.

1.2实验数据处理过程

Python 对数理统计和绘图功能的实现主要是通过Scipy包中的stats包，Numpy包和绘图Pylab包以及 pandas包来实现.其统计输出结果见表2、图1,具体实现过程代码如下：

pddata=pd.read_csv('data.csv') #读取表1中数据#

data=pddata["time"]

print data.describe() # 输出样本描述统计数据#

t = np.arange(1.5,2.5,0.1)

y =stats.norm(loc=2.0,scale=0.09) #根据样本描述统计数据的平均值和方差做期望拟合数据#

y2 = y.rvs(size=100)

pl.hist(data,t)# 绘制实验数据直方图#

pl.plot(t,y.pdf(t),label="experience",linestyle='--',color='g') #绘制经验或理论概率密度曲线#

p,t2 = np.histogram(y2,bins=10,normed=True)

t2 = (t2[:-1] + t2[1:])/2

pl.plot(t2,p,label="reality") # 绘制实际样本概率密度曲线#

pl.plot(t,y.cdf(t),label="experience",linestyle='--',color='g') #绘制经验或理论累计曲线#

pl.plot(t2,np.add.accumulate(p)*(t2[1]-t2[0]),label="reality") #绘制实际样本累计曲线#

表2　单摆周期T实验数据描述统计

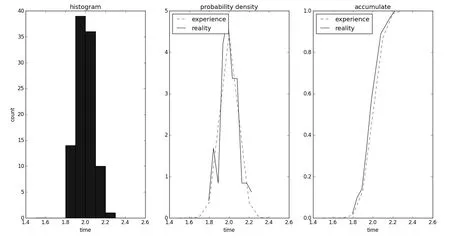
图1　单摆周期T实验样本统计直方图(左)、实际与理论比较的概率密度图(中)和累计曲线图(右)

1.3实验结果说明

从表2、图1可知：样本数据单摆周期T的平均值为2.00 s，方差为0.081，数据基本正态分布；样本与理论概率密度基本吻合；累计曲线也基本吻合,其线型陡峭说明测量次数增加不会太多地影响测量结果.

2霍尔效应实验数据回归分析

2.1数据的采集

霍尔效应实验是大学物理实验中电磁学部分的经典实验之一.包括2个实验过程[7]：测量霍尔电压(磁场强度)与螺线管轴上的位置的磁场分布，如表3数据；利用通电螺线管中心的均匀磁场测得霍尔器件灵敏度，如表4数据.

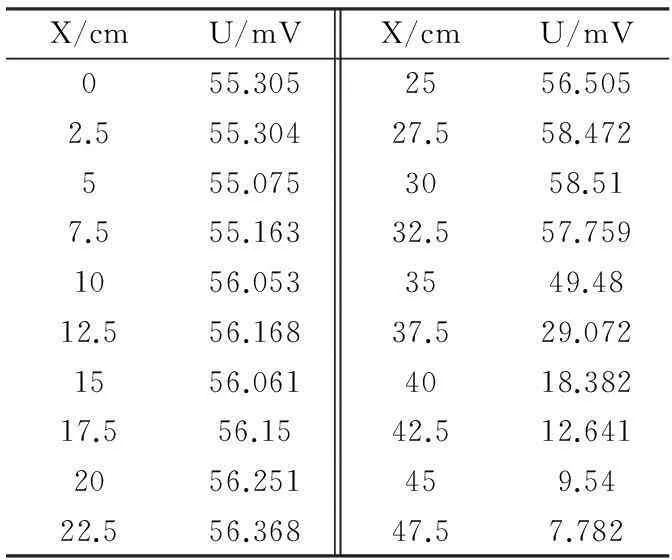
表3　霍尔电压-x轴坐标变化表

2.2实验数据处理过程

此类实验数据处理的主要过程是：根据实验数据的分布图利用逐步逼近法求出数据回归方程[8]，绘出拟合曲线并验证回归方程的拟合程度.Python回归分析主要利用sklearn.linear_model包实现，此外还需要 stats、Numpy包配合完成.根据已有经验，使用多项式(polynomial)回归对实验数据处理代码如下(统计输出结果见图2、3，表5)：

data=pd.read_csv('xu.csv') #读取表3数据，读取表4数据时换成“iu.csv"#

def rmse(y_test,y):#均方根误差,反应了测量数据偏离真实值的程度#

return sp.sqrt(sp.mean((y_test - y) ** 2))

def R2(y_test,y_true):#相关系数平方.介于[0～1]，0表示不如均值.1表示完美预测#

return 1 - ((y_test - y_true)**2).sum() / ((y_true - y_true.mean())**2).sum()

plt.scatter(x,y,s=5,label ="reality") #绘出原始数据散点图#

degree = [7,8,9] #回归多项式个数，由于霍尔灵敏度回归是线性回归，需要改为degree = [1]#

for d in degree:

clf = Pipeline([('poly',PolynomialFeatures(degree=d)),('linear',LinearRegression(fit_intercept=False))])#多项式回归#

clf.fit(x[:,np.newaxis],y)

y_test = clf.predict(x[:,np.newaxis]) #计算拟合数据#

print('rmse=%.2f,R2=%.2f,clf.score=%.2f' %(rmse(y_test,y),R2(y_test,y),clf.score(x[:,np.newaxis],y))) # clf.score就是多项式参数#

plt.plot(x,y_test,linewidth=2) #绘出拟合图形#

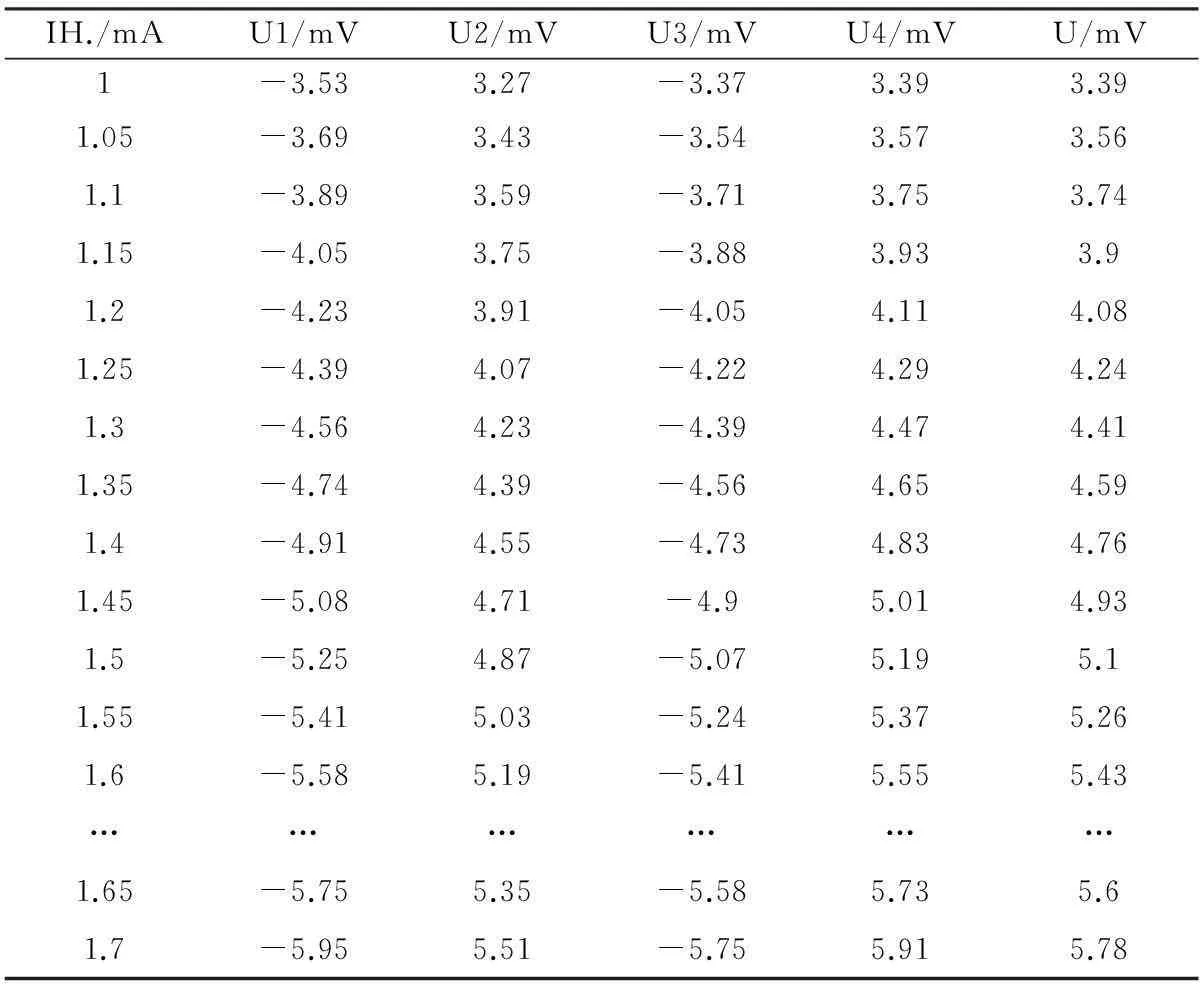
表4　霍尔电压-电流的变化表局部(U=(|U1|+|U2|+|U3|+|U4|)/4)

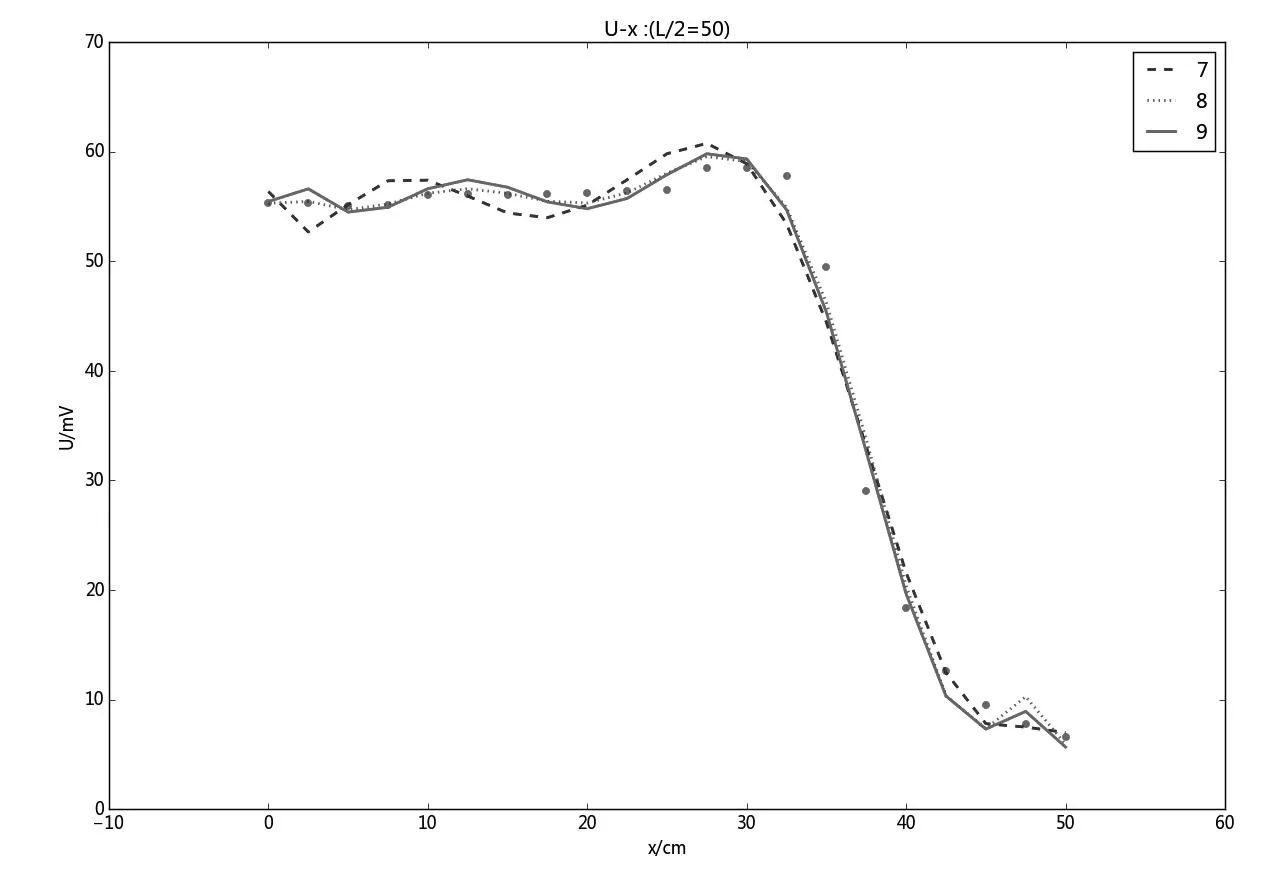
图2　螺线管内的磁场分布散点图与拟合曲线(表3数据)

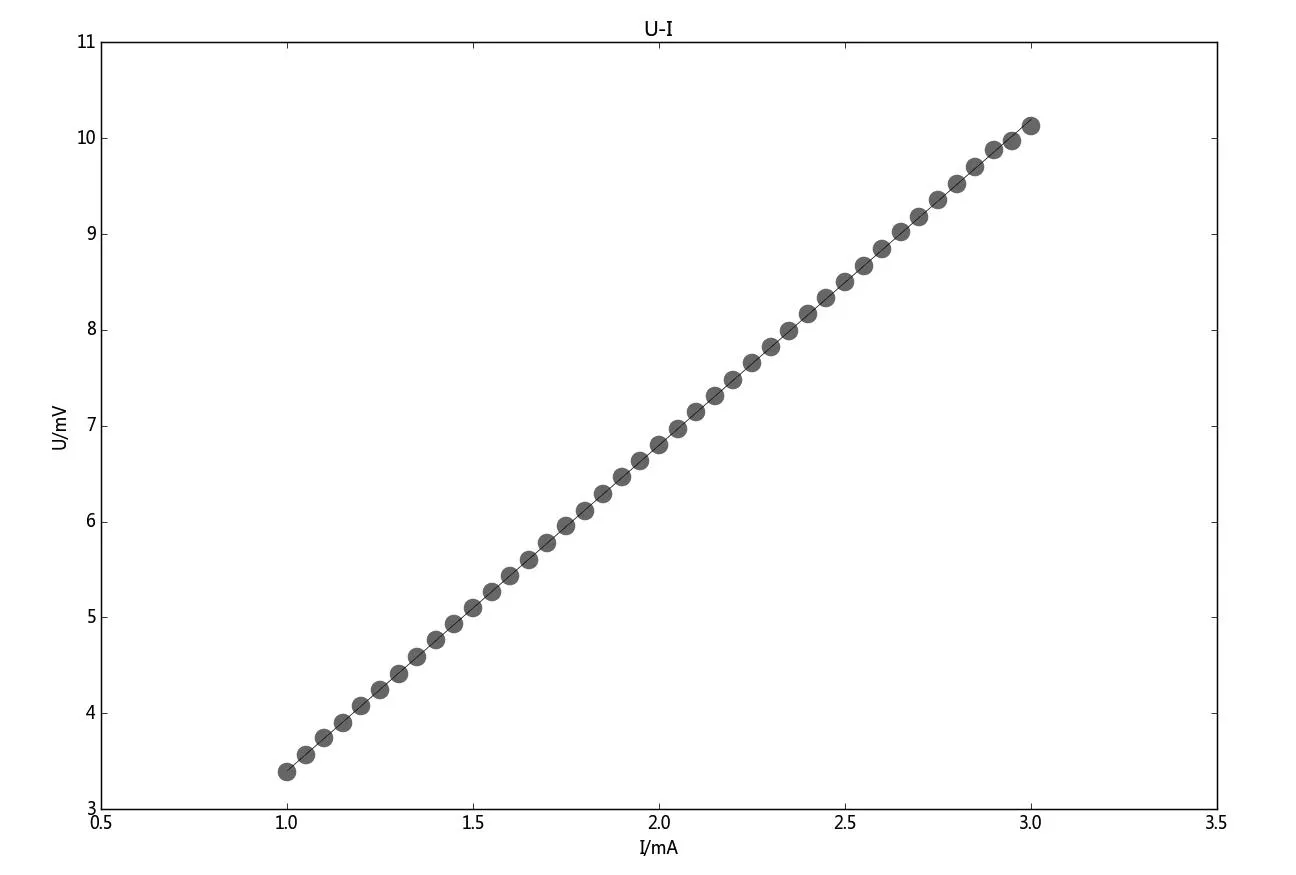
图3　霍尔电压随工作电流的变化散点图与拟合线(表4数据)

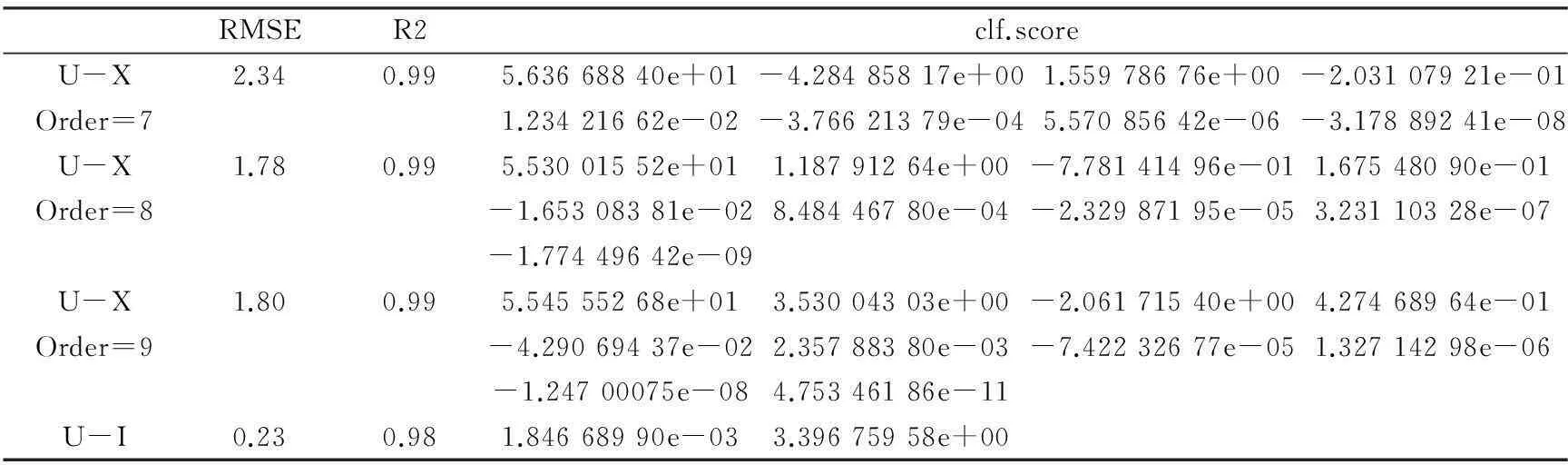
RMSER2clf.scoreU-X2.340.995.63668840e+01-4.28485817e+001.55978676e+00-2.03107921e-01Order=71.23421662e-02-3.76621379e-045.57085642e-06-3.17889241e-08U-X1.780.995.53001552e+011.18791264e+00-7.78141496e-011.67548090e-01Order=8-1.65308381e-028.48446780e-04-2.32987195e-053.23110328e-07-1.77449642e-09U-X1.800.995.54555268e+013.53004303e+00-2.06171540e+004.27468964e-01Order=9-4.29069437e-022.35788380e-03-7.42232677e-051.32714298e-06-1.24700075e-084.75346186e-11U-I0.230.981.84668990e-033.39675958e+00

2.3实验结果说明

从图2、表5可知,R2接近1,所有曲线拟合度都较好；7，8，9次多项式时均方根误差RMSE值分别为2.34,1,78，1.80;8次多项式RMSE值相对较小，说明其相对较好地拟合了螺线管内的磁场分布曲线.从图3、表5可知：霍尔器件的电压与电流存在线性关系，线性拟合度较好.

3单摆机械运动模拟

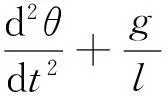
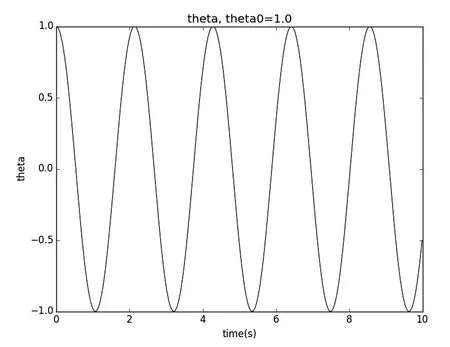
图4　odeint求解机械运动微分方程图

g = 9.8

def pendulum_equations(w,t,l):#解单摆微分方程#

th,v = w

dth = v

dv = - g/l * sin(th)

return dth,dv

t = np.arange(0,10,0.01) #生成时间连续点#

track = odeint(pendulum_equations,(1.0,0),t,args=(1.0,))#根据时间点，求解变化角度#

pl.plot(t,track[:,0])

4小结

从上述随机误差分布规律:数据回归分析和机械运动模拟的物理实验应用中可以看出Python使用灵活方便且资源丰富，可以推广到各类的物理和电子信息实验教学，以极大提高大学实验教学质量.

参考文献

[1] 百度百科.PYTHON[EB/OL].http://baike.baidu.com,2015-06-10.

[2] 张若愚.Python科学计算[M].北京:清华大学出版社,2012.

[3] 吴迪,张星海.Python在热敏电阻测量实验数据处理中的应用[J].大学物理实验,2013(10):97-101.

[4] 李小燕,冯卓宏,邱俊才.Matlab在大学物理教学中的应用[J].实验技术与管理,2010(11):124-126.

[5] 祝宇红,朱玮.MATLAB在近代物理实验数据处理中的应用[J].实验技术与管理,2006(4):38-40.

[6] 杨述武.普通物理实验[M].北京:高等教育出版社,2004.

[7] 郭悦韶.Matlab曲线拟合在霍尔效应实验中的应用[J].实验室科学,2013(8):24-26.

[8] 李飞.基于Matlab的霍尔效应实验数据处理[J].实验室研究与探索,2011(1):58-61.

[9] HYRY Studio.用Python做科学计算[EB/OL].http://sebug.net/paper/books/scipydoc/double_pendulum.html#id2,2015-06-10.

(责任编辑：张冬冬)

The research of university physics experiment data processing method based on Python language

ZHONG Zhiqiang

(School of Physical Science and Technology，Anshan Normal University,Anshan Liaoning 114007,China)

AbstractTaking the pendulum period measurement,solenoid Hall effect and the pendulum harmonic motion in university physics experiment as an example,this paper shows random error distribution,data regression analysis and application of methods of mechanical motion simulation by using Python language.The results show that experimental data processing is simple and flexible by this method,data graphical is intuitive and convenient,and this method should be widely used.

Key wordsPython;university physics experiment；data analysis

收稿日期2016-01-10

基金项目2014年辽宁省普通高等学校本科教育教学改革研究项目(UPRP20140403)：面向工程实践，提高专业核心能力——电子类专业；2016年辽宁省大学生创新创业训练计划项目(201510169012)：智能便捷式起吊机.

作者简介钟志强(1975-),男,辽宁辽阳人,鞍山师范学院物理科学与技术学院讲师,硕士.

中图分类号G434

文献标识码A文章篇号1008-2441(2016)02-0077-05