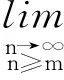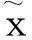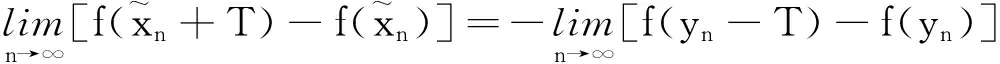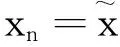关于吉氏习题集第752题解法的讨论

王 素 娟

(闽南理工学院，福建 石狮 362700)



关于吉氏习题集第752题解法的讨论

王 素 娟

(闽南理工学院，福建 石狮 362700)

摘要：文章指出了《Б.П.吉米多维奇数学分析习题全解》一书中第752题在论证中出现的不完善之处，给出了一种新的第752题证明方法，此方法过程完整，简约明白，易为数学分析学子所接受。

关键词：连续；有界；数列；极限

DOI：10.13757/j.cnki.cn34-1150/n.2016.02.030

近年来，东南大学出版社出版了好几套吉米多维奇《数学分析习题集》的题解，如毛磊等[1]编著的《Б.П.吉米多维奇数学分析习题集全解》，滕加俊[2]主编的《Б.П.吉米多维奇数学分析习题集精选精解》，郑琴等[3]主编的《吉米多维奇数学分析习题集精选详解》。除了郑琴等人的题解未选第752题外，其他两书对第752题给出了两种不同的证法，而且这两种证法被沿用至今。经仔细审视，笔者认为这两种证法有一些疏漏，应予以修补。

现将书中第752题的两个证法抄录如下，并加以讨论。对于原文中的两处小问题，笔者直接将其错误备注在该行的后面。

原题假设函数f(x)在区间(x0,+∞)是连续的并且有界，证明对任何一个数T，能求得序列xn→+∞，使得

(1)

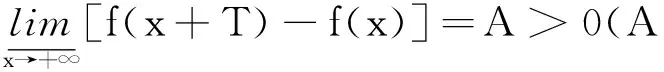
f(T+R)-f(R)>M，

f(2T+R)-f(T+R)>M，

f(nT+R)-f[(n-1)T+R]>M，从而f(nT+R)>(n-1)M+f(R)(注1：此式中的(n-1)应改为n)。这与f(x)在(x0,+∞)上有界相矛盾，因此，故存在序列xn→+∞使得

(注2：式中lim下方x→+∞应改为n→+∞)。

讨论1

(1)因为f(x)有界，所以A不会等于+∞；

(2)应给出f(x+T)-f(x)<0情况的结论；

(3)应续补在T<0情况下的论证。

f(x0+2T)-f(x0+T)≥ε1，

f(x0+3T)-f(x0+2T)≥ε1，

f(x0+nT)-f[x0+(n-1)T]≥ε1，

从而f(x0+nT)≥(n-1)ε1+f(x0+T)。这与f(x)在(x0,+∞)内有界相矛盾，故必存在自然数k1，使得|g(k1)|<ε1。

取x1=x0+k1T，则|f(x1+T)-f(x1)|<ε1。然后，取自然数p2>k1+1，通过考虑g(p2),g(p2+1),…，仿照上面的证明，可得k2>k1+1，使得|g(k2)|<ε2。

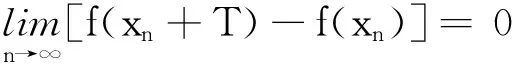
讨论2

(1)如同证法一，证者仍没有论证T<0的情况。再者说来，如果T<0，则x0+yT

(2)应论证g(y)在(x0,+∞)有无穷个零点和g(1),g(2),g(3),g(4),…都小于零的情况；

(3)在构造解的序列时，用了无穷多次反证法。有限次反证法的作用已有共识，至于无穷多次反证法的作用，目前还没有定论，所以无穷多次反证法最好不用；

(4)在论证过程中一直致力于构造解的序列xn=x0+knT(n→∞)，但用原题所提出的“求得序列xn→+∞”这一标准衡量，显得有些抽象迷离，是求而未得。

下面给出一个新的证法。

证明首先讨论T>0的情况。

(i)f(x+T)-f(x)不存在零点时。

因为f(x+T)-f(x)不存在零点，那么恒有f(x+T)-f(x)>0或者f(x+T)-f(x)<0，即f(x+T)>f(x)或f(x+T)

当f(x+T)>f(x)时有

f(x)

f(x+kT)<…，

取自然数m，使得mT>x0，则由上式得

f(mT)

于是得单调递增数列

(2)

(3)

即为所求。

类似地可以证明当f(x+T)

(ii)f(x+T)-f(x)存在零点且零点有上界的情况。

(iii)f(x+T)-f(x)存在零点且零点无界的情况。

(4)

(5)

讨论3根据此证明，对证法一进行必要的补充和修改，使得证法一能够成为一个完整的反证法。但按原题“求得序列xn→+∞”的要求，证法一是达不到的，它只能证明这种数列存在而已，故即使“完整”也不“究竟”。

参考文献:

[1] 毛磊, 滕兴虎, 寇冰煜, 等.Б.П.吉米多维奇数学分析习题集全解[M]. 1版. 南京: 东南大学出版社, 2014: 368-370.

[2] 滕加俊. Б.П.吉米多维奇数学分析习题集精选精解[M]. 2版. 南京: 东南大学出版社, 2015: 66-67.

[3] 郑琴, 超颖, 张瑰, 等. 吉米多维奇数学分析习题集精选详解(上册)[M]. 1版. 南京: 东南大学出版社, 2011.

DiscussionontheSolutionstotheExercise752inJi’sProblemSet

WANGSu-juan

(MinnanUniversityofScienceandTechnology,Shishi,Fujian362700,China)

Abstract:Itshowsouttheimperfectionsoftheexercise752inthebook“Б.П.JimmyDovichimathematicalanalysisproblemset”,andthengivesoutanewsolutiontotheexercise752.Thissolutioniscompleteandbrief,andwillbeenjoyedbythescholarsofmathematicalanalysis.

Keywords:continuous;bounded;sequence;limit

* 收稿日期：2015-10-31

作者简介：王素娟，女，福建仙游人，硕士，闽南理工学院讲师，研究方向为图论。E-mail: 63889375@qq.com

中图分类号：O171

文献标识码：A

文章编号：1007-4260(2016)02-0124-02

网络出版时间：2016-06-08 12:57网络出版地址：http://www.cnki.net/kcms/detail/34.1150.N.20160608.1257.030.html