电池置换站运营收益模型与策略

刘志雷，苗　瑞， 顾希垚， 吴易洲，赵　赫

(上海交通大学 机械与动力工程学院，上海200240)



电池置换站运营收益模型与策略

刘志雷，苗瑞， 顾希垚， 吴易洲，赵赫

(上海交通大学 机械与动力工程学院，上海200240)

摘要：为了使运营收益最大化，本文采用电池置换站的策略，从运营商的角度出发，建立了针对电池置换站运营的整数线性规划模型。该模型综合考虑了置换费用、置换站的电池拥有量、置换站的充放电能力以及置换站服务水平等因素。模型的求解主要采用Lingo编程技术，分析了模型的影响因素，得出了不同参数情况下对应收益的最大值和各置换站在各时间段对电池进行充放电的数量，同时进一步分析这些参数与运营收益之间的敏感关系。通过上述分析可以发现，该模型的提出可以使得运营商的投资风险最小化和收益的最大化，从而为制定合理有效的运营策略和电池管理提供有力指导。

关键词：置换站； 整数规划； 运营收益； 运营策略； 电池管理

内燃机汽车的尾气排放已经成为环境污染最主要的来源之一，新能源电动汽车的发展与推广应用是全世界各国家解决能源危机和环境污染的重要手段。电动汽车取代传统内燃机汽车的趋势很明显，然而在现实生活中主要有三大问题制约着电动汽车的发展与推广：续航里程短、充电时间长和电池购置成本高[1]。针对这3个阻碍因素，目前已经有很多相关的研究且都具有很强的可操作性。所谓续航里程就是电动汽车一次充电所能行驶的最大里程数。当用户考虑到电动汽车还没到达目的地电池电量就已经快用尽了，这种焦虑将会严重阻碍电动汽车的推广使用[2]。所以需要提供大量的充电设施来保障续航里程满足目的地要求，但是现在充电技术的发展还不能够满足电池的充电速度像加油站给汽车加油那样的迅速[3]，而且这样的充电行为具有很强的不确定性、分散性和随意性，给电网带来了十分复杂的影响[4-5]。HY Mak[6]提出电池置换站的建设，即在置换站内用已经充满电量的电池替换掉电量耗尽的电池，既可以满足航行的需要，又可以节约时间，同时便于电池集中管理，减少系统损失。电池的高额购置成本增加了电动汽车整体的购置费用，阻碍了消费者的购买行为。Sarah G Nurre等[7]和罗卓伟等[8]提出将车辆和电池分开考虑，用户只购买汽车，由专门的运营公司负责电池的更换、充电、保养和回收。在前面研究的基础上，刘坚[9]和姚建歆等[10]对电动汽车常规充电、快速充电、机械充电(电池置换)等类型的充电模式的优缺点进行了比较分析。刘金行[11]从现实可操作性的角度对电池置换站的建设、管理、标准化等环节作出分析，并在充电时间、电池流通管理、充电安全等方面进行了比较论证，证明了电池置换站的现实可操作性较强。陆婷婷[12]以充换电网络的日运营总费用最小为目标，研究了电池租赁的换电模式下充换电网络的运营调度问题。Haddadian G[13]考虑电动汽车对电力系统的影响，以电力系统单位时间运营成本最低为目标函数，建立了混合线性整数规划模型。张帝[14]以充电站内全天充电电费最低为目标，建立了充电变功率工况下基于分时电价的换电站经济运行模型。Sioshansi[15]提到换电站可以利用V2G技术，在用电低峰期对电池进行充电，在用电高峰期将电池电量释放回电网中，以平衡电网负荷。

综上所述，目前电动汽车电池领域的相关研究大都集中在电池充电技术、电网系统上，大多局限于电力系统、充电费用方面的模型研究，很少从运营方的角度去对置换站的运营进行建模分析，但是置换站的运营情况是投资运营方非常关心的。因此，本文站在运营方的立场，全方位考虑电池的置换费用、置换站的电池库存量、置换站充放电能力、置换站服务水平、V2G技术、分时电价等因素，建立相应的优化数学规划模型并利用相应的求解工具求解，为以后的电动汽车电池置换站的合理有效运营提供有力指导。

1问题描述

假定在不久的将来，电动汽车已经完全取代内燃机汽车占领整个汽车市场，那么电动汽车的电池置换站就如同现在的汽车加油站。所以，电动汽车前来置换电池的需求可以参考汽车到达加油站进行加油的需求量，也是服从泊松分布的。在此针对电池置换站的运营管理建立以运营收益最大化为目标的数学规划模型——整数规划。取研究时间长度T为24 h，即T=24；单位时间间隔为1 h，即T=1对应时间段00:00～01:00，T=2对应时间段01:00～02:00，T=3对应时间段02:00～03:00，以此类推T=24对应时间段23:00～00:00。为了便于研究，需要对置换站的运营作以下假设：1)国家智能电网已经建设完毕，V2G技术可以普遍使用；2)关于电动汽车的电池已实现标准统一化；3)电池充放电时间只需1 h，即如果电池在时刻t进行充电，那么到t+1时电池刚好充满电。

2 模型建立

考虑有n个置换站，每个置换站i的电池拥有量为Ii且恒定不变。每个置换站i的充放电接口数量为Li且充放电接口是通用的，即既可以从电网给电池充电又可以将电池电量释放回电网中。在任意时刻t，电费单价为pt元/kWh，既可表示电池充电所用成本，又可表示将电量释放回电网所获收益。dit表示置换站i在时刻t时电池置换的需求量。为用户提供一次电池置换服务的费用为s元，且在时间T内不会发生变化。变量xit表示在时间t第i个置换站完成的置换数量，如果用户到达置换站由于没有满电量电池剩余而不能完成置换，则客户就会流失；客户流失的同时还会影响服务水平λ。

在每个置换站，电池只有2种状态：满电和亏电。满电量电池的状态有3种：等待、被置换或者进行放电动作；亏电电池的状态有2种：等待和正在被充电。用变量fit表示时间t第i个置换站满电量电池的数量，那么亏电电池数量就是Ii-fit。变量yit和zit分别表示在时间t第i置换站充、放电的电池数。在现实中充放电行为不会同时发生，否则放电缓解电网负荷将失去意义，但在模型中可以将单独进行的充放电行为放在一起，互相抵消以实现收益的量化。α表示一块电池进行一次充放电交换的电量，即为电池容量，不妨设定为30 kWh。假设有一个电动汽车电池置换站的投资运营商，投资负责一块区域的运营，其目标就是该区域所有置换站每天运营收益最大化。收益来自电池置换费用和放电所获利润，成本包括充电费用和服务损失。模型如下。

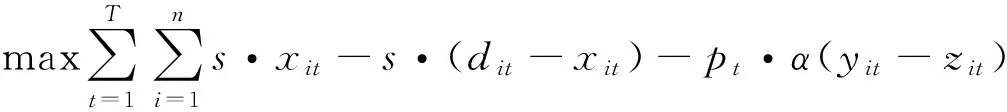
s.t.

yit≤Ii-fit,i=1,2，…，n;t=1,2，…，T。

(1)

xit+zit≤fit,i=1,2，…，n;t=1,2，…，T；

(2)

fi(t+1)=fit-xit-zit+yit,

i=1,2，…，n;t=1,2，…，T-1；

(3)

yit≤Li,i=1,2，…，n;t=1,2，…，T；

(4)

zit≤Li,i=1,2，…，n;t=1,2，…，T；

(5)

xit≤dit,i=1,2，…，n;t=1,2，…，T；

(6)

xit≥λdit,i=1,2，…，n;t=1,2，…，T；

(7)

0≤fit≤Ii,i=1,2，…，n;t=1,2，…，T；

(8)

fi0=Ii,i=1,2，…，n;t=1,2，…，T；

(9)

xit,fit,yit,zit∈{Z+∪0},

i=1,2，…，n;t=1,2，…，T。

(10)

至于电池的仓储和维护成本是静态的，可归为固定成本，无需进行统筹管理，故模型中并没有包含仓储和维护成本。目标函数是对投资运营方投资的所有置换站在全天的运营收益最大化进行研究，综合考虑了置换费用、充放电价格和充放电行为、置换站电池数和置换站充放电能力。约束条件(1)限制充电行为；约束条件(2)限制电池置换和放电数不会超过满电量电池数；约束条件(3)等式计算t+1时刻满电量电池数；约束条件(4)和(5)限制充放电行为应该不大于置换站的接口数；约束条件(6)限制置换量应该小于等于置换需求量；约束条件(7)满足置换站的服务水平；约束条件(8)限制满电量电池数不会超过置换站电池拥有量；约束条件(9)表示初始运营状态下置换站的所有电池都是满电量的；约束条件(10)约束各变量均为正整数或者0。

3 实例分析

有一投资商要在上海投资建设电动汽车电池置换站，但不知道置换站建成后的运营收益如何？单次置换费用定价多少比较合理？有哪些因素会影响运营收益？这些影响因素对收益的影响敏感程度如何？如何安排电池的充放电以充分利用分时电价的政策？这些问题都可以根据本文的模型进行求解得到解决方案。投资方对上海某加油站进行了调研统计，获得了24 h各时间段车辆前来加油的车辆数，该数据可以作为模型中的置换站i在时刻t时电池置换的需求量dit，见表1。

表1　dit取值表

目前很多城市都采用分时电价来平缓用电负荷，将电价分为峰段、平段和谷段3个阶段。如果置换站能够合理安排充电时间，将充电移至平谷段，可以节省大量充电费用。利用2014年上海夏季的分时电价作为pt，见表2。

表2　上海市10 V工商业及其他用电夏季分段及

使用数学规划求解工具lingo编程对模型进行求解，分析置换站个数为n、置换站电池拥有量为I、置换站接口数为L、单次置换费用为s以及服务水平为λ等参数对运营收益的敏感关系以及各置换站在各时间段的充放电安排。基于以上参数的取值，让n分别取5、6、7、8；I分别取100、150、200、250；s分别取25、30、35、40；λ分别取80%、85%、90%、95%。假定置换站的充电接口数L是I的一半，则L分别为50、75、100、125。探究不同的置换站数n、电池拥有量I、置换费用s和服务水平λ对运营收益的影响并找出各因素的敏感性大小，不同参数对应的运营收益如图1所示。

由图1可知，随着置换站数n、置换站电池拥有量I和置换费用s的增加运营收益都是随之增大的，但增加幅度有所不同，也就是说运营收益对不同参数变化的敏感性有所不同；然而服务水平λ发生变化对运营收益却无影响，这表明在最优条件下一定能满足服务水平的要求。根据图1可知其敏感性由大到小依次为s、I、n，这样的试验结果和实际情况也是基本吻合的。运营方根据此模型合理地增加置换费用s和适当地增加置换站的电池数I便可以获得十分可观的收益；运营方拥有的置换站数量n增大其收益也会有相应的增加，但增加置换站所需的建设投入成本比较大，可能得不偿失。所以，运营方可以根据此模型并结合自身的特点制定出合理有效的策略，提高自身的市场竞争力。

任取一组参数n=5，I=100，s=25，λ=0.8，对该参数下模型的求解结果进行详细分析，其分析结果如图2所示。由图2(a)可以看出各置换站在各时间段应该进行充电的电池数，由图2(b)可以看出各置换站在各时间段应该进行放电的电池数，这样的策略安排可以使得资源利用最合理，运营收益最大化。所以本文的模型也可以很好对电池进行充放电管理，为置换站的健康运营提供科学的依据。

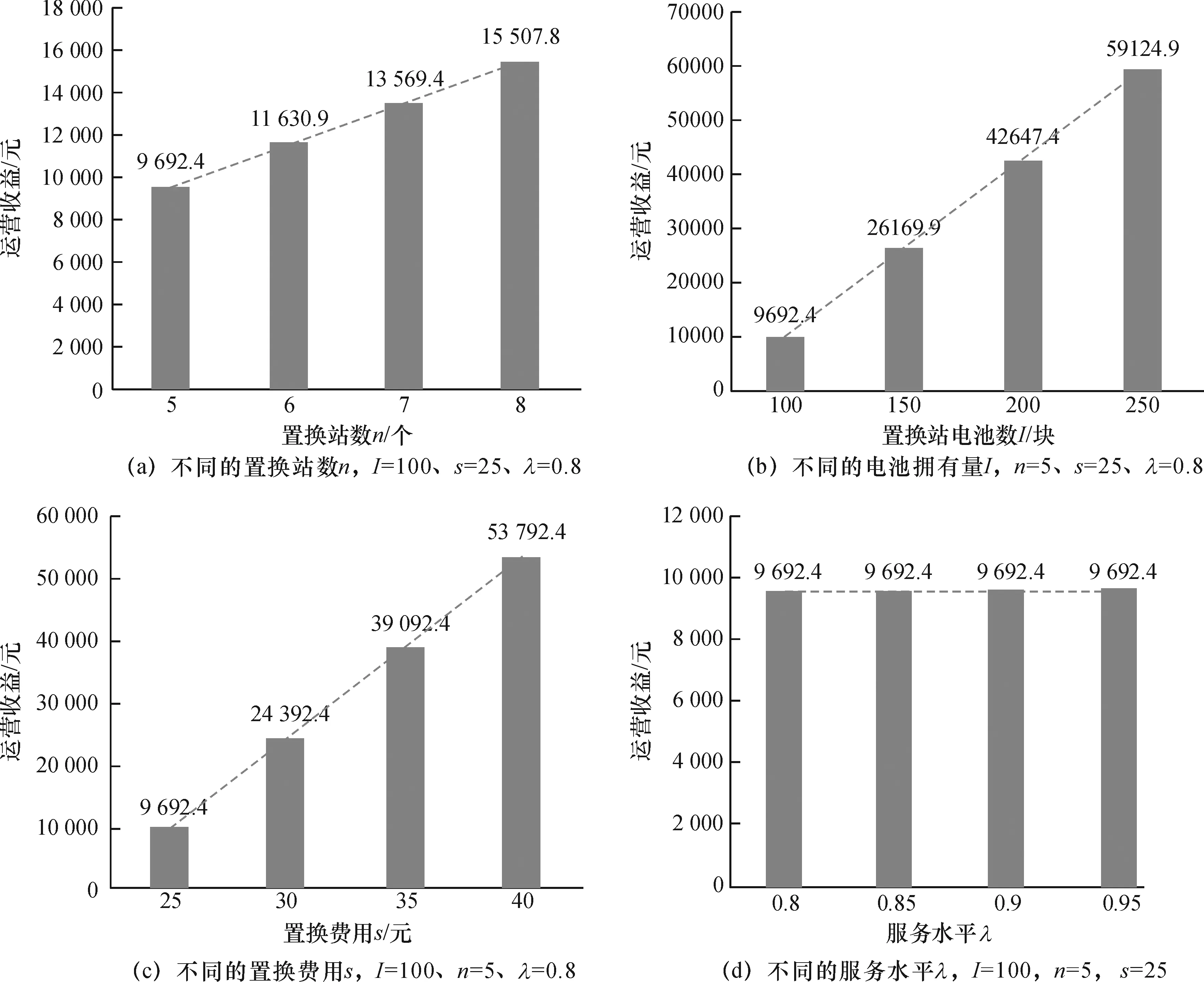
图1不同参数对应的运营收益

Fig.1Operation profit by different parameters

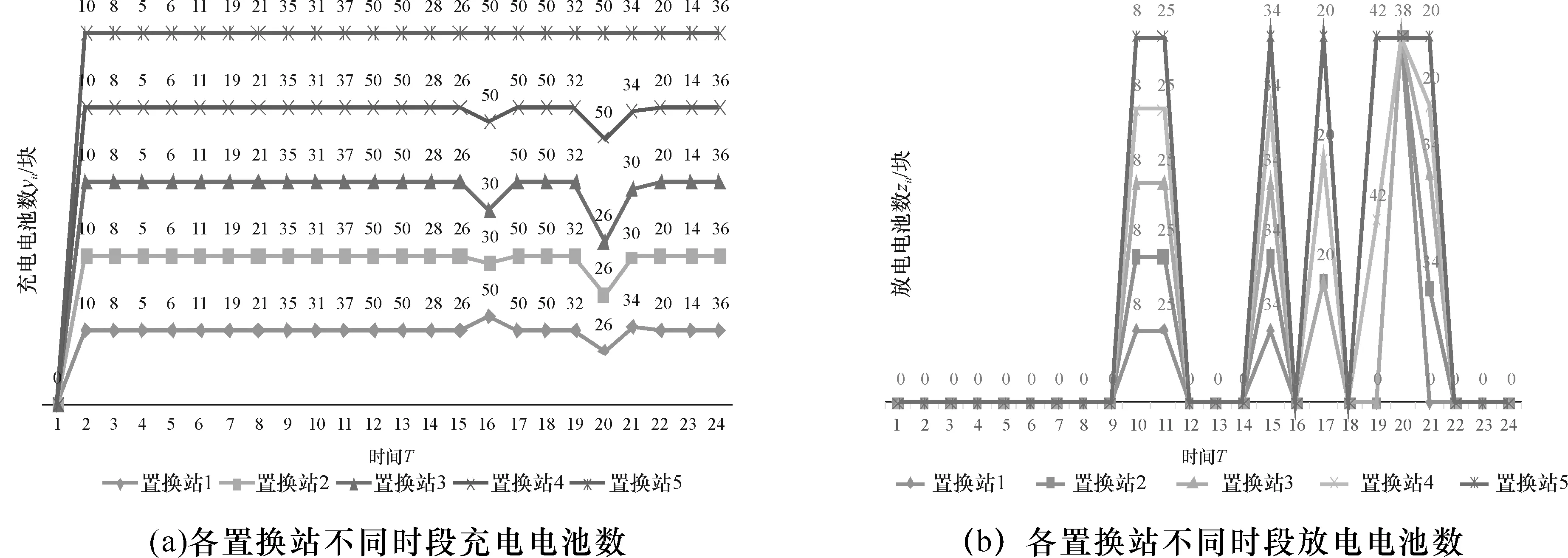
图2　各置换站不同时间段电池充放电情况

4结语

在新能源电动汽车推广过程中所遇到的各种阻碍及相应解决方案的基础上，以运营方为主体建立了以运营收益最大化为目标的电池置换站运营模型。运用Lingo编程对模型进行求解，然后对求解结果进行分析，从而得出置换站各参数对运营收益的影响敏感程度，运营方可据此制定出合理有效的运营策略。与此同时，对模型的求解也可得出置换站在一天中的各个时间段电池充放电的数量，为电池的充电管理提供了科学的指导，既平衡了电网负荷，又减少了充电成本。后续的研究可以进一步考虑建设投资成本，根据投资回收期确定置换站规模、运营定价等问题。

参考文献：

[1] AVCI B, GIROTRA K, NETESSINE S. Electric vehicles with a battery switching station: Adoption and environmental impact[J]. Management Science, 2014, 61(4): 772-794.

[2]YU A S O, SILVA L L C, CHU C L, et al. Electric vehicles: struggles in creating a market[C].Technology Management in the Energy Smart World (PICMET). Protland, OR: IEEE: 2011.

[3]BOTSFORD C, SZCZEPANEK A. Fast charging vs. slow charging: Pros and cons for the new age of electric vehicles[C]. Norway: Stavanger, 2009:1-9.

[4]LOPES J A P, SOARES F J, ALMEIDA P M R. Integration of electric vehicles in the electric power system[J]. Proceedings of IEEE, 2011, 99(1):168-183.

[5]LIU Z, WEN F, LEDWICH G. Optimal siting and sizing of distributed generators in distribution systems considering uncertainties[J]. IEEE Transactions on Power Delivery, 2011, 26(4): 2541-2551.

[6]MAK H Y, RONG Y, SHEN Z J M. Infrastructure planning for electric vehicles with battery swapping[J]. Management Science, 2013, 59(7): 1557-1575.

[7]NURRE S G, BENT R, PAN F, et al. Managing operations of plug-in hybrid electric vehicle (PHEV) exchange stations for use with a smart grid[J]. Energy Policy, 2014, 67: 364-377.

[8]罗卓伟, 胡泽春, 宋永华, 等. 换电模式下电动汽车电池充电负荷建模与有序充电研究[J]. 中国电机工程学报, 2012, 32(31): 1-10.

LUO Zhuowei, HU Zechun, SONG Yonghua，et al．Study on charging load modeling and coordinated charging of electric vehicles under battery swapping modes[J]. Proceedings of the CSEE, 2012, 32(31):1-10.

[9]刘坚. 电动汽车充电方式和商业运营模式初探[J]. 汽车工程师, 2011 (1): 19-22.

LIU Jian. A preliminary study on charging infrastructure development and business operation models[J]. Auto Engineer, 2011 (1): 19-22.

[10]姚建歆, 王媚, 罗伟明. 电动汽车充电系统建设应用分析研究[J]. 华东电力, 2008, 36(8): 107-110.

YAO Jianxin, WANG Mei, LUO Weiming. Construction and application of charging systems for electric mobiles[J]. East China Electric Power, 2008, 36(8): 107-110.

[11]刘金行. 建设电动汽车电池更换式充电站的可操作性分析[J]. 科技广场, 2010(3): 226-229.

LIU Jinhang. Operability analysis of electric cars battery replacement charging station construction[J]. Science Mosaic, 2010(3): 226-229.

[12]陆婷婷, 高赐威. 电动汽车充换电网络优化调度通用模型研究[J]. 电网技术, 2014, 38(10): 2700-2707.

LU Tingting, GAO Ciwei. A general model for optimal scheduling of battery charging and renewal network[J]. Power System Technology, 2014, 38(10): 2700-2707.

[13]HADDADIAN G, KHALILI N, KHODAYAR M, et al. Optimal scheduling of distributed battery storage for enhancing the security and the economics of electric power systems with emission constraints[J]. Electric Power Systems Research, 2015, 124: 152-159.

[14]张帝，姜久春，张纬戈，等. 基于遗传算法的电动汽车换电站经济运行[J]. 电网技术, 2013, 37(8): 2101-2107.

ZHANG Di, JIANG Jiuchun, ZHANG Weige, et al. Economic operation of electric vehicle battery swapping station based on genetic algorithms[J]. Power System Technology, 2013, 37(8): 2101-2107.

[15]SIOSHANSI R, DENHOLM P. The value of plug-in hybrid electric vehicles as grid resources[J]. Energy Journal, 2010, 31(3): 1-23.

Operating Profit Model and Operation Strategy of Battery Exchange Station

LIU Zhilei, MIAO Rui, GU Xiyao, WU Yizhou, ZHAO He

(School of Mechanical Engineering, Shanghai Jiaotong University, Shanghai 200240, China)

Abstract：From the operator’s point of view, an integer linear programming model for the operation of the battery exchange station is established to maximize operation profit by using the policy of battery exchange station. The factors such as the exchange fee, the battery inventory, the charge and discharge capacity and the service level of the exchange station are comprehensively considered in the model. The model is solved based on the Lingo program. And then the optimal profits and the number of charge and discharge batteries can be obtained for different parameters. Additionally, the sensitivity relationship between the different parameters and the operation profits is further analyzed. Through the analysis, it can be found that the proposed model can minimize the risk of the operator′s investment and maximize operation profit. Therefore, it can provide a strong guidance for the operator to make a reasonable and effective operation strategy and battery management.

Key words：battery exchange station; integer programming; operation profit; operation strategy; battery management

收稿日期：2015- 10- 23

基金项目：国家自然科学基金资助项目(51435009)； 上海交通大学大学生创新实践计划资助项目(IPP11023)

作者简介：刘志雷(1989-)，男，安徽省人，硕士研究生，主要研究方向为服务与运作管理.

doi:10.3969/j.issn.1007- 7375.2016.03.014

中图分类号：TM911

文献标志码：A

文章编号：1007-7375(2016)03- 0085- 05