基于WIM数据的上海某斜拉桥锚固结构寿命评估

张　军， 胡明敏， 王永涛

(南京航空航天大学 航空宇航学院， 江苏 南京　210016)



基于WIM数据的上海某斜拉桥锚固结构寿命评估

张军， 胡明敏， 王永涛

(南京航空航天大学 航空宇航学院， 江苏 南京210016)

[摘要]根据上海某斜拉桥的动态称重系统(WIM)所采集的车辆信息数据，以索梁和索塔锚固区的钢锚箱作为研究对象，分别计算不同轴型的汽车加载时钢锚箱的应力变化历程，采用雨流计数法建立疲劳细节的应力谱，参考BS5400确定疲劳细节的S-N曲线，结合线性累积损伤准则公式计算钢锚箱的疲劳寿命，并对该结果做出分析和说明。

[关键词]动态称重系统； 钢锚箱； S-N曲线； 疲劳寿命

1概述

大型桥梁是在交变载荷下长期工作的，动载荷使得钢桥结构中产生反复变化的应力，这种反复变化的应力会使钢桥结构在应力集中处或存在缺陷处的局部产生微小裂纹并使裂纹扩展，最终导致疲劳破坏。能否准确计算出钢桥损伤值大小和结构剩余寿命是对钢桥疲劳评估的最直接目的，并作为对钢桥是否采用有效措施进行维护、加固确保其安全运营的有力参考依据[1-3]。

斜拉桥的上部结构是由塔、梁、拉索3个主要部分组成[4]，上海某斜拉桥采用钢箱梁作为主梁，而大跨度钢箱梁斜拉桥中常见的索梁锚固形式主要有锚管式、耳板式、锚拉板式和锚箱式连接[5]，上海某斜拉桥采用的就是锚箱式锚固结构。拉索与主梁和主塔的锚固部位的构件就是关键的传力部位，这些锚固点的可靠性直接影响整桥的工作状态。拉索锚固区阶段是主塔与拉索相连的部分，是主塔的核心部位，主塔拉索锚固区的主要作用是将所有拉索的索力通过该部位均匀、安全的传递到塔柱的受力部位，该部位受力形式复杂、应力集中现象严重，是关系到整桥安全的重要部位。所以对锚固结构进行疲劳寿命分析是非常重要的。

2有限元模型

整体建模见图1，因采取的建模方式所限，无法分车道进行加载，所以将六车道的车流量数据合并为上行与下行两车道的数据[6]。上海某斜拉桥索梁锚固区阶段拉索的布置形式为空间扇形双索面，顺桥向主梁索距为15m，主梁与拉索采用钢锚箱锚固形式。索塔锚固区阶段总长为56.55m，共23个钢锚箱节段，阶段高2.3～3.2m，节段1位于索塔锚固区的底部，阶段23位于索塔锚固区的顶部。第23#-2#索依次锚固在钢锚箱上，0#、1#索锚固于锚固区底部混凝土上表面，见图2。

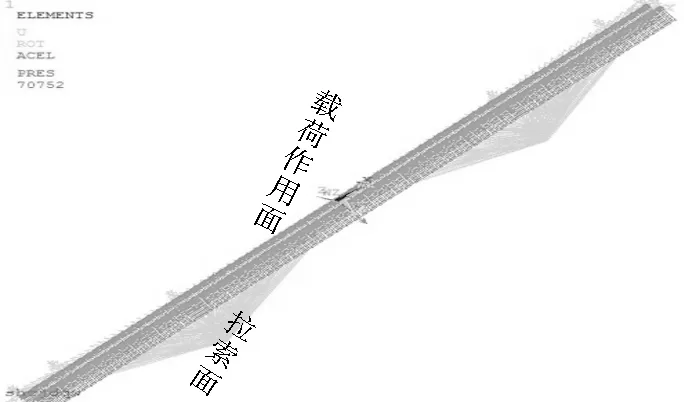
图1　整桥有限元模型Figure 1　The finite element model of the whole bridge

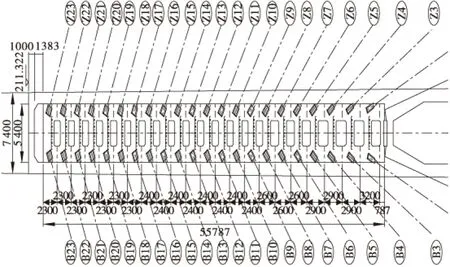
图2　索塔锚箱整体布置图Figure 2　Overall arrangement of the tower anchorage

对于所观测的拉索，由于总共有192根拉索，本文只选取与所分析索梁锚箱和索塔锚箱相关的拉索。分别是PES7-151索梁锚箱相连的b1拉索，与PES7-163相连的b2拉索，与PES7-337相连的b16和b17拉索，与PES7-409相连的b23拉索，索梁锚箱的分析所选拉索均为西南位置的拉索。除此之外每个索塔锚箱还与四根拉索相连，分别为z16、z17、z23、b16、b17和b23拉索，如图3，表1所示。

根据整体模型可提取出每根拉索的索力，图4为7-337锚箱在对应拉索z17作用下的应力分布总图，载荷大小选择远期梁端恒载索力，大小为6 315kN。

选择拉索b17对应的索塔阶段进行计算分析。

图3　本文所研究的几根典型拉索的位置Figure 3　Positions of the typical cables in this paper

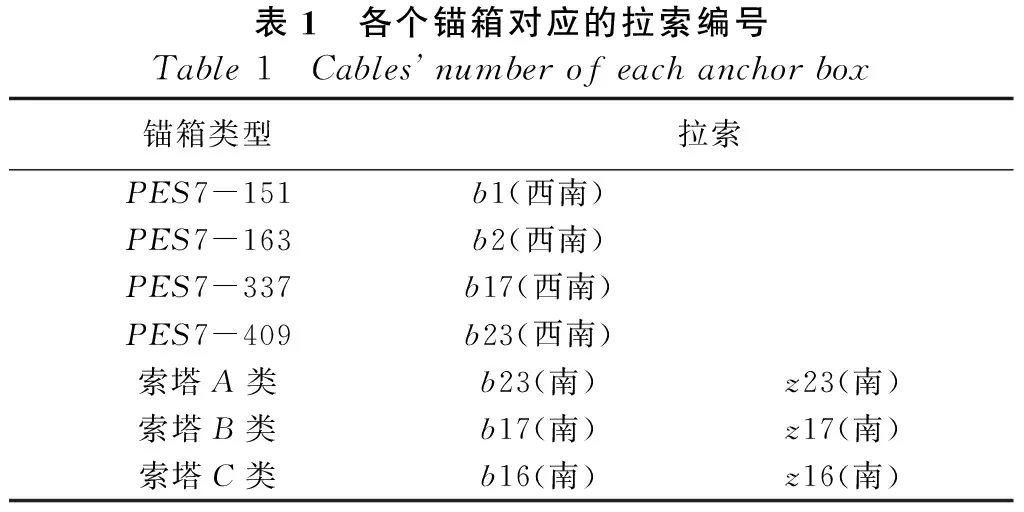
表1 各个锚箱对应的拉索编号Table1 Cablesnumberofeachanchorbox锚箱类型拉索PES7-151b1(西南)PES7-163b2(西南)PES7-337b17(西南)PES7-409b23(西南)索塔A类b23(南)z23(南)索塔B类b17(南)z17(南)索塔C类b16(南)z16(南)

上海某斜拉桥索塔锚固区是混凝土与钢锚箱的组合结构，采用内置式钢锚箱[7，8]。拉索的水平分力大部分由钢锚箱的侧板和端板承受，少部分由塔壁混凝土承受[9，10]。如图5所示整个钢锚箱的应力分布。

图4　索梁钢锚箱应力分布云图Figure 4　The stress cloud of anchorage

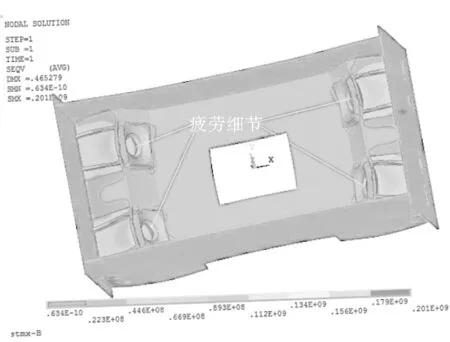
图5　索塔锚箱应力分布云图Figure 5　The stress cloud of tower anchorage

3应力谱

将等效车辆载荷加载于ANSYS整桥模型的上行或者下行车道，由此得到192根拉索的应力变化历程。索力正是本文所研究的锚固区结构的载荷，将索力的应力历程加载于锚固结构即得到疲劳细节的应力历程。

根据应力历程，采用雨流计数法来提取出钢锚箱的疲劳细节应力谱，但因其技术条件偏于复杂，并且数据量较大，因此选择用编程来实现该方法。该方法主要是数据压缩和循环数提取两个步骤，本文采用MATLAB来实现。通过雨流计数法得到应力幅值，并把对应的该模型车的车流量作为循环次数，由此实现从应力历程到应力谱的过程。仅给出2012年8月这个时间段索梁锚箱和索塔锚箱疲劳细节点的应力谱(见图6，图7)。

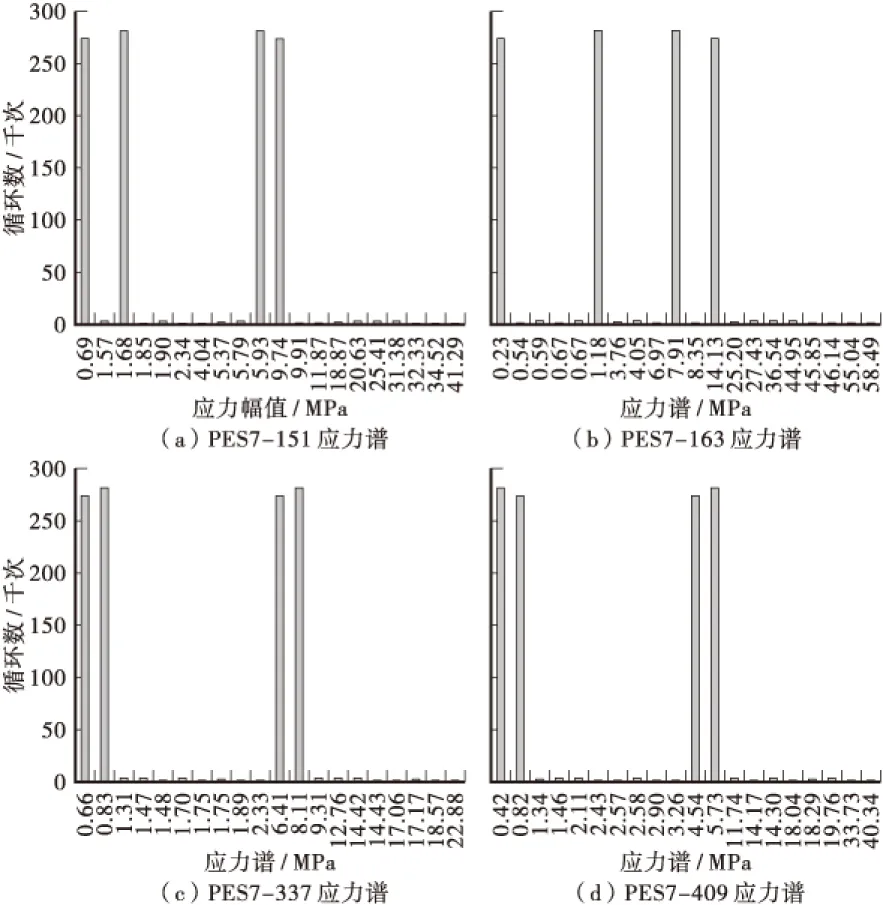
图6　2012年8月索梁锚箱细节应力谱Figure 6　The stress spectrum of anchorage details

图7　2012年8月索塔锚箱细节应力谱Figure 7　The stress spectrum of tower anchorage details

4建立S-N曲线

疲劳曲线是表示应力范围(或最大应力、应力幅)与疲劳寿命之间关系的曲线，简称为S-N曲线。通过S-N曲线，可以确定材料的疲劳极限值，疲劳极限越高，材料抗疲劳性能就越好[11-13]。首先要建立外载荷与寿命之间的关系S-N曲线来评价和估算桥梁细节疲劳寿命或疲劳强度。

NSα=C

(1)

式中：α和C为材料常数；N为在应力幅为S的疲劳寿命。

在英国桥梁规范BS5400[14]中，针对不同细节分级，将式NSα=C改为：

(2)

式中：N为在应力幅值为σr时的疲劳寿命；k0为有统计分析结果的均值决定的常数项；m为logσr-logN均值线斜率的倒数；Δ为logN标准方差的反对数的倒数；d为低于中线值的标准方差数，与某一失效概率相对应。

查BS5400第十部分附录表9可得k0、m、Δ；附录表10可得d。

BS5400的疲劳设计曲线公式：

(3)

根据BS5400细节构造分级准则，查表可知本文所分析的钢锚箱的疲劳细节为F2级，查表得到k0=1.23×1012，m=3.0，Δ=0.592，图8为依据公式(3)绘制出细节在不同失效概率下的S-N曲线，实线为大于疲劳极限σ0段的S-N曲线，其斜率为1/m，虚线为小于疲劳极限σ0段的S-N曲线，其斜率为1/(m+2)，兼顾疲劳极限以下应力幅值对疲劳损伤的贡献[15]。

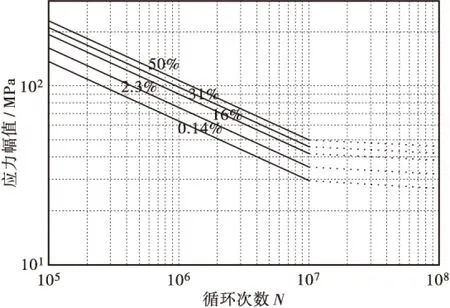
图8　不同失效概率下S-N曲线Figure 1　S-N curve under different failure probability

在图8中，疲劳极限σ0为按照公式(4)计算，得到107对应的许用应力幅值(疲劳极限)。各失效概率下的疲劳极限值可查表。

(4)

5钢锚箱细节损伤计算

疲劳损伤D用Miner线性损伤累积理论计算，并考虑对疲劳极限以下应力循环的修正。

(5)

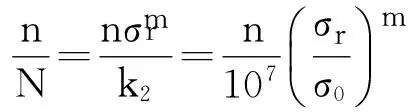
(6)

(7)

式中：n1，n2，…，nn为桥梁已使用期间，应力幅值为σ1，σ2，…，σn所对应的循环次数；σ0为应力幅值(疲劳极限)。

基于篇幅，仅给出索梁锚固区PES7-337钢锚箱2012年8月载荷谱及损伤累积过程(见表2)。

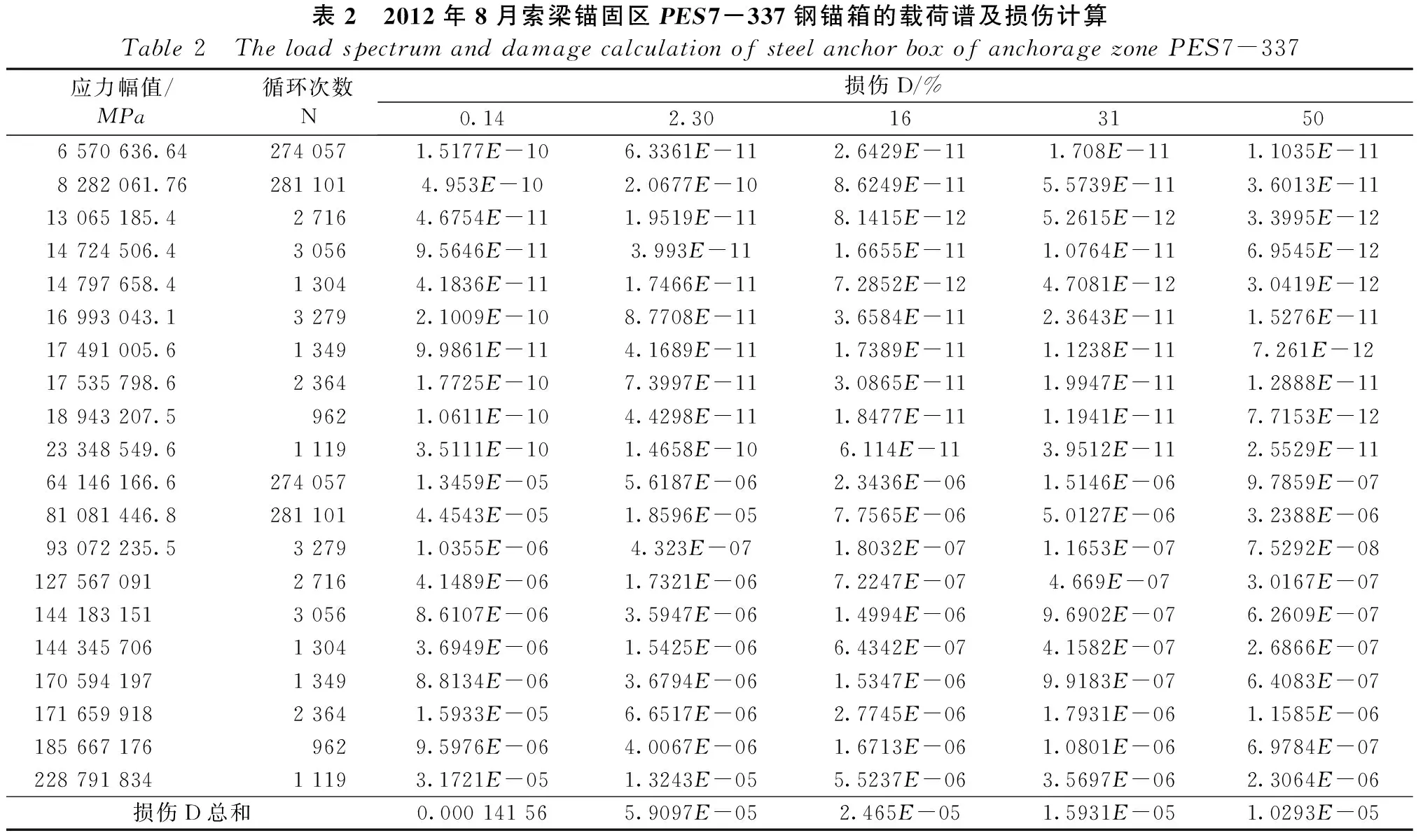
表2 2012年8月索梁锚固区PES7-337钢锚箱的载荷谱及损伤计算Table2 TheloadspectrumanddamagecalculationofsteelanchorboxofanchoragezonePES7-337应力幅值/MPa循环次数N损伤D/%0.142.301631506570636.642740571.5177E-106.3361E-112.6429E-111.708E-111.1035E-118282061.762811014.953E-102.0677E-108.6249E-115.5739E-113.6013E-1113065185.427164.6754E-111.9519E-118.1415E-125.2615E-123.3995E-1214724506.430569.5646E-113.993E-111.6655E-111.0764E-116.9545E-1214797658.413044.1836E-111.7466E-117.2852E-124.7081E-123.0419E-1216993043.132792.1009E-108.7708E-113.6584E-112.3643E-111.5276E-1117491005.613499.9861E-114.1689E-111.7389E-111.1238E-117.261E-1217535798.623641.7725E-107.3997E-113.0865E-111.9947E-111.2888E-1118943207.59621.0611E-104.4298E-111.8477E-111.1941E-117.7153E-1223348549.611193.5111E-101.4658E-106.114E-113.9512E-112.5529E-1164146166.62740571.3459E-055.6187E-062.3436E-061.5146E-069.7859E-0781081446.82811014.4543E-051.8596E-057.7565E-065.0127E-063.2388E-0693072235.532791.0355E-064.323E-071.8032E-071.1653E-077.5292E-0812756709127164.1489E-061.7321E-067.2247E-074.669E-073.0167E-0714418315130568.6107E-063.5947E-061.4994E-069.6902E-076.2609E-0714434570613043.6949E-061.5425E-066.4342E-074.1582E-072.6866E-0717059419713498.8134E-063.6794E-061.5347E-069.9183E-076.4083E-0717165991823641.5933E-056.6517E-062.7745E-061.7931E-061.1585E-061856671769629.5976E-064.0067E-061.6713E-061.0801E-066.9784E-0722879183411193.1721E-051.3243E-055.5237E-063.5697E-062.3064E-06损伤D总和0.000141565.9097E-052.465E-051.5931E-051.0293E-05

6不同概率下的疲劳寿命计算

已知桥梁细节疲劳寿命C为：

(8)

式中：T是桥梁已服役时间。

当箱梁细节损伤值的负量级较高时，说明其具备的疲劳寿命比较长，且细节损伤值随着失效概率的增大而变小，按照公式(8)由索梁和索塔钢锚箱的损伤总和计算得到对应的寿命评估值，其中载荷是按照月份采集的，因此将计算出的疲劳寿命除以当月天数然后乘以365天进行转换，得到单位是年的疲劳寿命。可算出2011年9月、2012年2、8月的数据。根据Miner损伤法则中的损伤累积，将这3个月份的损伤累积进行加和，以此作为公式(8)中的总损伤，可以计算出4个索梁锚箱和3个索塔锚箱总的疲劳寿命如表3所示。

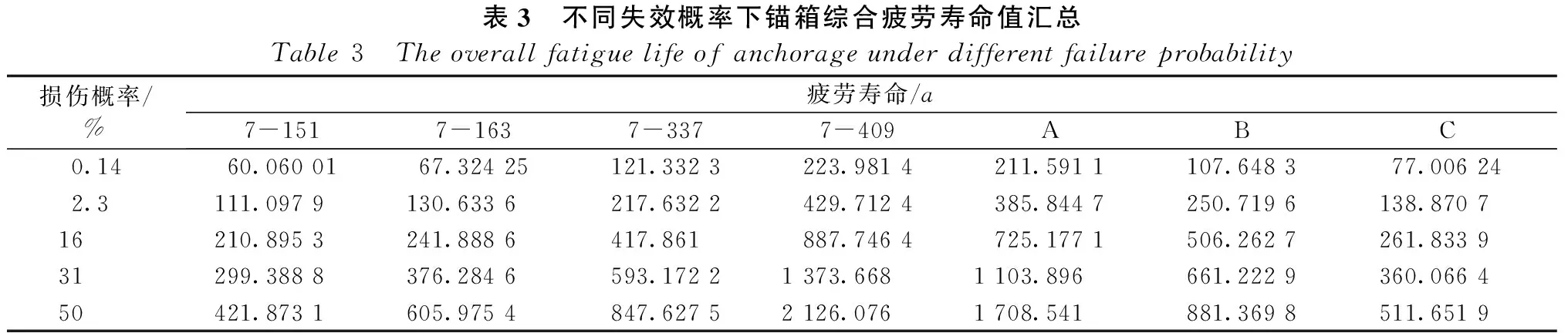
表3 不同失效概率下锚箱综合疲劳寿命值汇总Table3 Theoverallfatiguelifeofanchorageunderdifferentfailureprobability损伤概率/%疲劳寿命/a7-1517-1637-3377-409ABC0.1460.0600167.32425121.3323223.9814211.5911107.648377.006242.3111.0979130.6336217.6322429.7124385.8447250.7196138.870716210.8953241.8886417.861887.7464725.1771506.2627261.833931299.3888376.2846593.17221373.6681103.896661.2229360.066450421.8731605.9754847.62752126.0761708.541881.3698511.6519

7结语

桥梁结构的剩余寿命评估取决于很多因素，其中失效概率的选取对预测结果有重大影响。根据“公路桥梁可靠度研究”推荐，失效概率宜在5%～25%之间。根据上表失效概率的分布本文选择失效概率为2.3%和16%的寿命评估预算值进行分析。在2.3%损伤概率下，钢锚箱的疲劳寿命大致分布在110～430a之间，并且除了7-409索梁锚箱之外大部分锚箱的疲劳寿命都是在110～220a之间，考虑到上海长江隧桥的设计使用寿命有100a，已服役近4a(到本文的统计数据日期为止)，说明本文计算的寿命还是比较可靠的。在损伤概率为16%的情况下，疲劳寿命大多数分布在210～510a之间。由此类推，整个桥梁的索梁钢锚箱以及索塔钢锚箱在服役期具有较高的安全性。

[参考文献]

[1]HelmerichR，HerterJ，BrandesK.Fullscalelaboratoryfatiguetestsonrivetedsteelbridges.WorkshopLausanne：LABSE，1997.

[2]KunzPM，KulakGL.Fatiguesafetyofexistingsteelbridge.Extendingthelifespanofstructures.SanFrancisco：LABSESymposium，1995.

[3]BruehwilerE，SmithIFC，HirtMA.Fatigueandfractureofrivetedbridgemembers.JournalofScructuralEngineering，1990，116(1)：198-214 .

[4]严国敏.现代斜拉桥[M].成都：西南交通大学出版社，1996.

[5]满洪高.大跨度钢斜拉桥索梁锚固结构试验研究[D].成都：西南交通大学，2007.

[6]SchluneH，PlosM，GylltoftK.采用静态和动态法改进有限元模型进行桥梁评估[J].钢结构，2009(8)：040.

[7]周扣琴.部分斜拉桥索塔锚固区局部应力分析[D].南京：南京林业大学，2010.

[8]何震.部分斜拉桥拉索车载疲劳研究及索塔锚固分析[D].武汉：华中科技大学，2007.

[9]吴新元.斜拉桥钢桥塔索塔锚固区受力分析[J].山西建筑，2009，35(11)：328-329.

[10]刘路.斜拉桥索塔锚固区节段受力特性研究[D].重庆：重庆交通大学，2009.

[11]郭健，孙炳楠.桥梁健康监测中的关键性问题和损伤识别方法[J].公路，2006(4)：108-116.

[12]胡明敏，唐静静，魏平.一种SN曲线移动法的寿命分析模型[J].河海大学学报：自然科学版，2003，31(1)：60-63.

[13]胡明敏.用等效平均损伤模型计算剩余寿命方法的研究[J].航空学报，2000，21(3)：262-266.

[14]英国标准BS5400.钢桥、混凝土桥及结合桥(第十篇)[M].成都：西南交通大学出版社，1987.

[15]方义庆.基于疲劳寿命计的大型钢桥疲劳监测关键技术研究[D].南京：南京航空航天大学，2006.

ThelifeEstimationofAnchoringStructureofShanghaiCertainCable-stayedBridgeBasedonWIMData

ZHANGJun，HUMingmin，WANGJongtao

(NanjingUniversityofAeronauticsandAstronauticsofAeronauticsandAstronautics，Nanjing，Jiangsu210016，China)

[Abstract]According to the data of vehicle information from the Weigh-in-Motion system(WIM)of Shanghai Certain Cable-stayed Bridge.The research objects are the steel anchor box of anchorage zone and tower anchorage area.Define the stress change course of all selected anchor boxes undertook the different vehicle load.After calculate stress change course via Rain Flow Counting method we get the stress spectrum of fatigue details.Refer to the S-N curve of fatigue details depend on BS5400 and linear cumulative damage rule formula，calculate the fatigue life of all the anchor boxes and make an analysis and description of this result.

[Key words]weigh-in-motion； steel anchor box； S-N curve； fatigue life

[收稿日期]2015-02-02

[作者简介]张军(1992-)，男，安徽宣城人，硕士，研究方向：疲劳断裂、结构健康监测。

[中图分类号]U 448.27

[文献标识码]A

[文章编号]1674-0610(2016)03-0208-04