深挖教材核心例题 充分揭示数学本质*——以人教版《数学(选修2-1)》“椭圆”为例

●步一隽

(杭州第四中学下沙校区　浙江杭州　310018)

●徐　剑

(杭州第十四中学凤起校区　浙江杭州　310006)



深挖教材核心例题充分揭示数学本质*
——以人教版《数学(选修2-1)》“椭圆”为例

●步一隽

(杭州第四中学下沙校区浙江杭州310018)

●徐剑

(杭州第十四中学凤起校区浙江杭州310006)

摘要：课堂教学中“如何增强学生对数学本质的认识和理解”，其中一个有效途径是做好课堂中的例题教学和习题练习.为此，文章提出一个“核心例题”的概念，通过对核心例题的开发与设计，把数学的学术形态转化为学生易于接受的教育形态.

关键词：数学本质；核心例题；椭圆定义

张奠宙教授指出：“数学教育的核心是让学生掌握数学的本质.”何为数学本质？站在教育者的角度看，数学本质应该包括数与形的客观规律、知识所处的背景、地位、作用、联系、区别及其蕴含的数学思想方法、思维过程[1].强调对数学本质的认识是本次高中课改的一个重要理念.课堂教学中，在坚持适度形式化的前提下，引导学生对数学本质的理解，能够让学生深刻认识数学概念的内涵，使他们自觉地将个体思维融入数学知识的形成过程，不断体会蕴含其中的思想方法[2].

如何增强学生对数学本质的认识和理解？在中学数学教学中，笔者认为其中一个有效途径是做好课堂中的例题教学和习题练习.例题教学阶段往往是整堂课中学生思维最活跃、参与度最高、自主性最强的阶段.它不但能使学生积极掌握数学基础知识与基本方法，还能揭示数学知识的内在联系，促进学生对概念进一步的理解与掌握，同时也提供了进行思维训练的环境——培养学生思维的深度、广度和灵活性.

教师在一堂课中都会围绕教学目标安排一系列的例题与练习来达成目标的实现，但往往更多关注知识的记忆、解答过程的规范与类型方法的掌握，忽视对概念与知识产生过程的揭示和蕴含其中的数学思想方法的挖掘.教师的思维水平很大程度上决定着学生的思维水平.在此，笔者提出一个“核心例题”的概念.一组例题中应有一个或若干个核心例题，通过对核心例题的开发与设计，把数学的学术形态转化为学生易于接受的教育形态，引导学生自主探索，经历数学知识的发展过程，发现数学知识之间的联系与区别，理解数学概念内涵与本质，体会蕴涵在其中的思想方法.

作为学生接触最多的一本数学资料，高中数学教材的编写符合学生的认知规律，在数学知识的系统性和探究课题的创新性方面有较强的功能.教材上的例题是平日教学中核心例题的一个重要且丰富的来源.下面笔者结合人教版《数学(选修2-1)》“椭圆”一节[3]，谈谈在教学中对核心例题的设计与实践，借此抛砖引玉，引起同行的讨论.

1用核心例题揭示数学概念的联系与本质

案例1人教版《数学(选修2-1)》第47页例6的教学设计.

设计意图一方面巩固“直接法”求动点的轨迹以及示范规范的解题过程；另一方面为椭圆第二定义的引入作铺垫.

设计意图从学生的最近发展区入手，对问题作一般化推广.归纳椭圆的第二定义，并向学生介绍椭圆准线和焦半径概念与公式，为今后的应用作准备.

问题2你能发现2个定义的联系吗？可以先回顾一下椭圆第一定义方程的推导.

设计意图从一个例题形式突然引出椭圆的第二定义，就像“魔术师帽子里跑出一只兔子”，学生难以理解这第二定义怎么来的？与第一定义有什么联系呢？设计这一开放式问题，引导学生进行主动探究，同时考虑到课堂节奏，因此给出了方向性的提示.

课堂的实际效果很好.有的学生翻开了课本，重温书上的推导过程；有的学生拿出了纸笔，开始演算.学生们发现了2种方法：

方法1(根据教材)

回到椭圆方程的初始形式

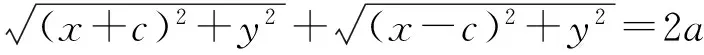
将左边一个根式移项，平方，整理得

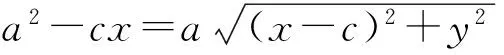
2边同除以a，得

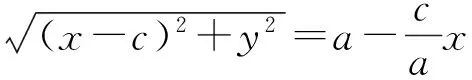
即

或

方法2(新的突破)

回到椭圆方程的初始形式

(1)

有理化分子，得

整理得

(2)

由式(1)和式(2)解得

即

或

同样的推导，当带着特定的目标和不同的意识回视，产生了截然不同的效果.学生亲历这样的探究过程，不难发现椭圆第一定义的初始方程、第二定义的初始方程、焦半径公式虽形式不同，本质上却是等价的，即椭圆的第一定义与第二定义是统一的.

2用核心例题揭示数学思想方法与思维的形成

案例2人教版《数学(选修2-1)》第41页例2与例3的教学设计.

例2在圆x2+y2=4上任取一点P，过点P作x轴的垂线段PD，D为垂足.当点P在圆上运动时，线段PD的中点M的轨迹是什么？为什么？

设计意图一方面促进学生掌握求轨迹方程中的“相关点法”和“直接法”；另一方面对圆和椭圆的伸缩变换呈现几何直观，为后续探究作铺垫.

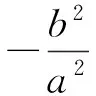
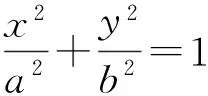
设计意图对2个例题作一般化推广和逆向探究，推动学生从具体形象思维向抽象逻辑思维迈进.对圆方程和椭圆方程作形式化的变换研究，为学生探究圆与椭圆之间性质迁移作铺垫.

问题5对照图1和图2，你能从椭圆与圆的关系角度解释2者性质之间的联系吗？

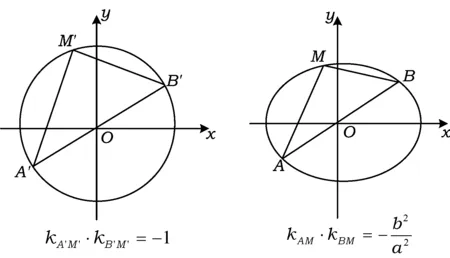
图1 图2

设计意图跳出问题处理的常规思路，向学生引入椭圆问题圆化处理的策略，揭示2者的内在联系，渗透转化化归的思想.

问题的起点是圆，结论指向是椭圆，这种合情推理的问题情境，让学生感到自然而亲切.问题以探究形式呈现，更容易激发学生的兴趣与主动性.同时有了前面的逐层铺垫，这种思路的产生自然而流畅.

同理可得

于是

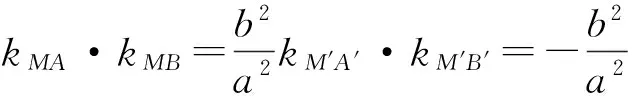
问题6如图3与图4，类比平面几何中圆的“垂径定理”，圆心与弦中点的连线垂直，在斜率存在的情况下，2条直线的斜率之积为-1，探究：在椭圆中直线AB与直线OM的斜率之积(其中M为弦AB的中点).

图3 图4

设计意图本题是留给学生的课后探究作业，强化应用圆化策略的意识.

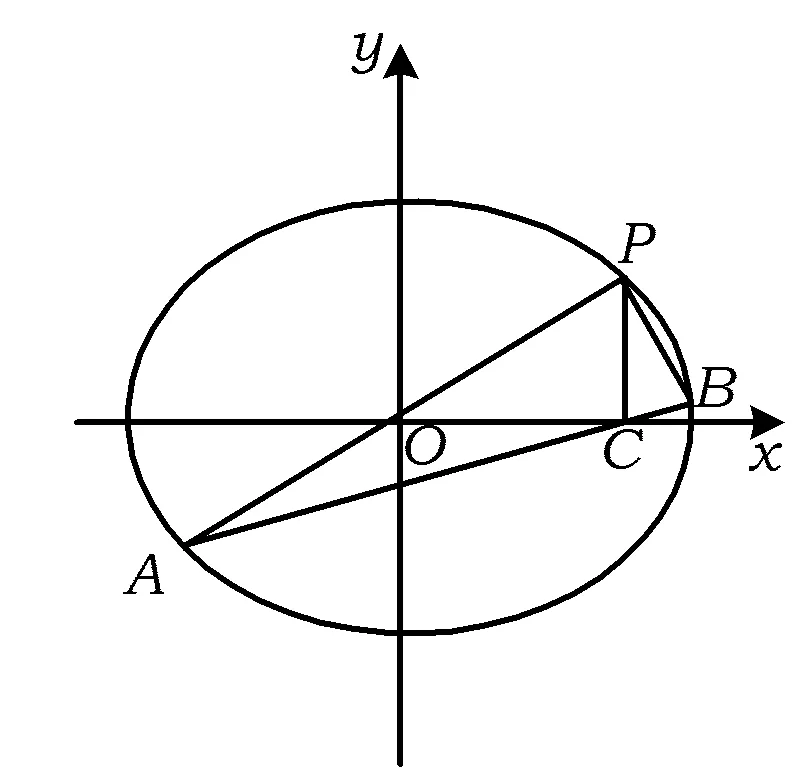
图5

设计意图本题是2011年江苏省数学高考第18题的第3)小题.高考中不变的是知识，变化的是情景的呈现形式、问题的组合结构，而且众多高考题来自于对教材例题的二次开发.

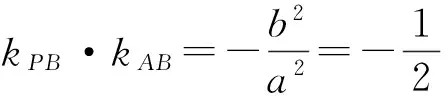
kPA·kPB=-1，

只需证

kPA=2kAB,

即证

kPA=2kAC.

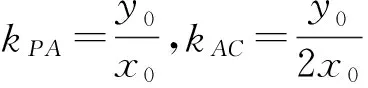
核心例题教学的本质是从教学角度出发的解题，是对常规例题教学的有效补充.对于核心例题的教学设计，笔者认为在研读课程标准和教材的基础上，可以考虑以下这些问题：

1)问题的背景是什么？知识定位和作用在哪里？[4]

2)问题可以作一般化的推广吗？

3)问题可以作逆向(条件和结论顺序重组)的推广吗？

4)可以改变问题呈现的方式吗？

5)问题与其他数学知识有哪些联系？

6)问题的设计是否为学生提供有价值的数学理解和思维方式？

7)问题的设计是否为学生的自主活动提供空间？

8)问题如何评价？

核心例题教学推动学生经历知识形成的过程，引导学生发现数学的规律、知识之间的内在联系和问题解决的途径，促进数学思维系统的正迁移.用清楚的、自然的数学去打动学生，加深对数学本质的理解和对数学学科的热爱，让学生的探究更“深”更“动”，让课堂的数学味更浓.

参考文献

[1]施洪亮.高中生数学创新素质培育的实践与思考[M].上海：上海教育出版社，2011.

[2]中华人民共和国教育部.普通高中数学课程标准[S].北京：人民教育出版社，2003.

[3]人民教育出版社课程教材研究所.数学(选修2-1)[M].北京：人民教育出版社，2007.

[4]胡典顺,汪钰雯，纪静萍，等.作为教育任务的数学解题[J].数学通讯，2013(11)：1-5.

修订日期：*收文日期：2016-04-06；2016-05-06

作者简介：步一隽(1974-)，男，浙江杭州人，中学一级教师.研究方向：数学教育.

中图分类号：O123.1

文献标识码：A

文章编号：1003-6407(2016)07-01-03