基于图像连续表示的角点检测

娄联堂，韦茜妤，陈佳骐，方自成

(中南民族大学 数学与统计学学院，武汉 430074)



基于图像连续表示的角点检测

娄联堂，韦茜妤，陈佳骐，方自成

(中南民族大学 数学与统计学学院，武汉 430074)

摘要为研究基于数字图像连续表示的角点检测方法，利用弦理论给出了离散数字图像的连续表示形式，利用快速付里叶变换实现了离散数字图像的连续表示和重建.通过计算小矩形区域的积分对直线段进行了检测.将角点的响应函数定义为平行四边形面积的大小，利用检测出的有向直线段，实现了对角点的检测.运用不同于传统的离散图像角点检测方法进行了角点检测实验，结果表明：它对图像的噪声有较强的适应性.

关键词数字图像连续表示；直线检测；角点检测

特征提取在计算机视觉、图像处理和机器视觉中一直是一个重要研究点，而角点作为图像的一个重要特征，长期以来备受研究者关注，也取得了很多研究成果.一般地，角点被认为是二维图像亮度变化最剧烈或图像边缘曲线上曲率值最大的像素点，能很好地被区分出来，具有旋转不变性和不随光照条件变化而改变的优点[1].在计算机视觉中，角点是指位于某一平面边界曲线上的点，且在各个方向上同时取得大的梯度.同边缘和直线等特征相比，角点具有提取过程简单、结果稳定、提取算法适应性强等特点.角点检测有广泛的应用，例如在一组相关图像中进行目标跟踪、立体图像之间对应关系的匹配、运动目标的检测等.经过30多年的发展，产生了大量的角点检测算法，取得了很大的突破和进展，但这方面的研究一直在进行中[2].角点检测的方法主要有两种[3，4]：⑴ 基于图像边缘的方法[5]：先提取图像信息的边缘，然后再求角点，例如，基于小波变换模极大的角点检测、基于边界链码的角点检测；⑵ 基于图像灰度的方法[5-7]，例如，Moravec算法、Harris算法、SUSAN算法等.

本文采用不同于传统角点检测算法的思想，通过对数字图像基于弦理论的连续表示形式直接进行积分，用纯解析方法检测直线，然后通过计算过像素点的任意两条有向直线段所构成平行四边形面积的最大值(并定义其为角点响应函数)，寻找角点疑似点，检测某像素点是否为角点，再根据预定的阈值确定角点，从而达到检测角点的目的.这样检测出的角点较准确，而且能够克服以往算法对图像边缘和噪声点的敏感性，算法过程相对简单、易于实现.

1数字图像的连续表示

对于离散图像f(x,y)(x=1,2,…，w,y=1,2,…，h,其中w，h分别为图像的宽度和高度)，可令在x=0,x=w+1,y=0,y=h+1时，f(x,y)=0，对其四周进行扩展.此外考虑图像的带宽是有限的，并且当m,n较大时, 高频分量Fm,n较小，可忽略不计，假设m,n的最大值分别为M,N，则数字图像f(x,y)可近似表示为：

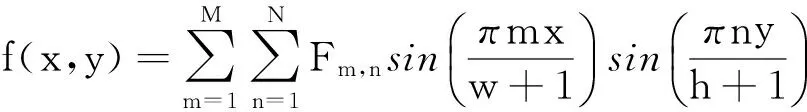
(1)

其中x=0,1,…,w+1,y=0,1,…,h+1.

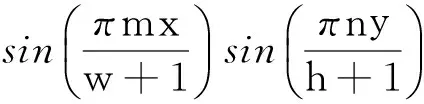
(2)

由数字图像f(x,y)通过(2)式计算得到Fm,n后，代入(1)式得到重建后的图像连续表示[8]为：

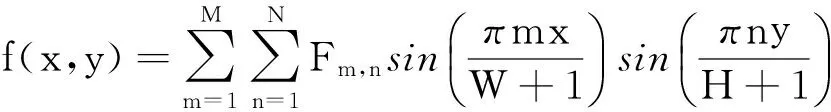
(x,y)∈[0,W+1]×[0,H+1],

(3)

其中W,H分别为重建后的图像宽度和高度.

再用付里叶变换计算Fm,n及重建图像f(x,y).(2) 式可化为如下形式：

Fm,n=-F(f11(x,y)-f12(x,y)-f21(x,y)+

f22(x,y)),

其中F表示二元函数的付里叶变换，x=0,1,…,2w+1,y=0,1,…,2h+1.

f22(x,y)=

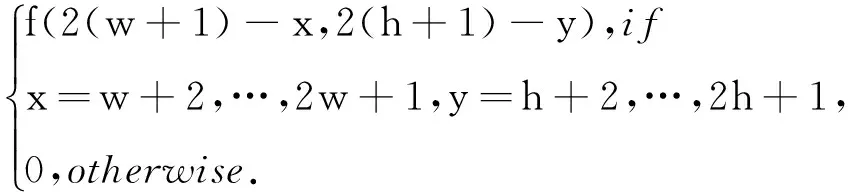
接着，将上面计算出的Fm,n，代入(1)式重建图像，设重建后图像的宽度为W，高度为H，与上述类似，可计算得：

其中F-1表示二元函数的付里叶逆变换，m=0,1,…,2W+1,n=0,1,…,2H+1,

2对连续表示的图像用积分方法进行直线检测

设区域D是以直线段L：

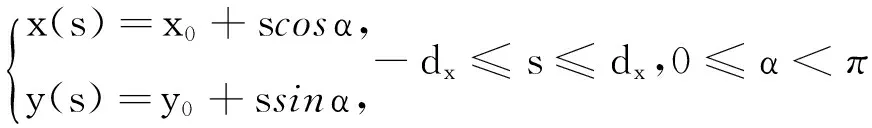
为中心线、宽度为2dy的矩形区域，在图像上表示一条有宽度的直线段(假设区域全部在图像内部).为检测这样的直线段，记：

h(x0,y0,α,dx,dy)=∬Df(x,y)dxdy.

(4)

作坐标变换：

则区域D为：-dx≤x′≤dx,-dy≤y′≤dy，0≤α<π,注意到该变换的Jacobian行列式为1，因此，将图像的连续表达形式代入(4)式，得：

h(x0,y0,α,dx,dy)=∬Df(x′cosα+y′sinα+x0,

-x′sinα+y′cosα+y0)dx′dy′=

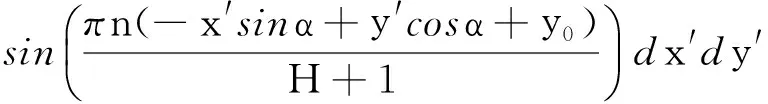
cos(a21x′+a22y′sinα+b2)dx′dy′,

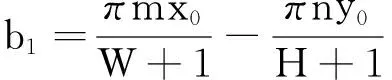
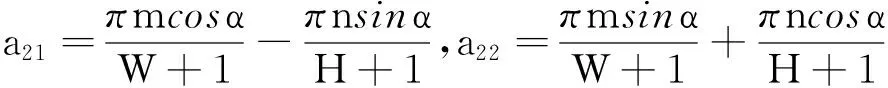
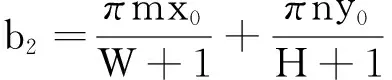
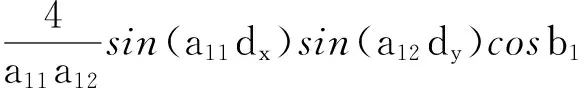
于是h(x0,y0,α,dx,dy)=

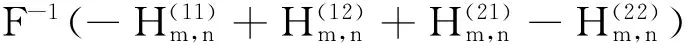
其中，F-1表示二元函数的付里叶逆变换，m=0,1,…,2W+1,n=0,1,…,2H+1.

为了验证用积分方法基于图像连续表示进行直线检测的可行性及其效果，本文在Windows7下使用Matlab7.10.0进行实验.

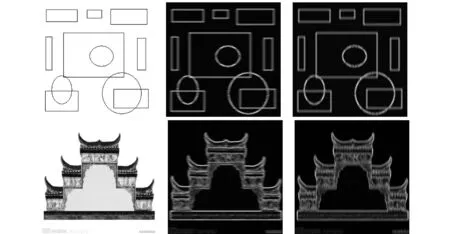
(a) 原图　　　　　　　(b) α=0°直线检测　　　　　(c) α=90°直线检测图1　直线检测Fig.1　Line detection

3角点检测

设区域D是以直线段L：

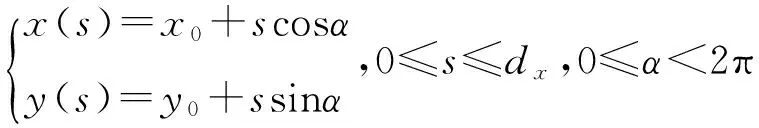
为中心线、宽度为2dy的矩形区域，在图像上表示一条有宽度的直线段(假设区域全部在图像内部).为检测这样的直线段，记：

h(x0,y0,α,dx,dy)=∬Df(x,y)dxdy.

区域D也可以改写为是以直线段L′：

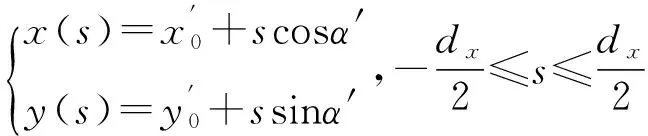
为中心线、宽度为2dy的矩形区域，其中：

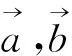
S(x0,y0,α1,α2,dx,dy)=h(x0,y0,α1,dx,dy)h(x0,y0,α2,dx,dy)|sin(α2-α1)|.

(5)

角点响应函数定义为：

(6)

在直线检测的基础上，对于每个像素点(x0,y0)，根据(5)式计算出以该点为端点的任意两条有向直线段所构成的平行四边形的面积，利用(5)和(6)式计算响应函数T(x0,y0,dx,dy)的值，判断T(x0,y0,dx,dy)是否大于预定的阈值，若大于，则该点为角点；否则该点不是角点.

4实验结果与分析

本文在Matlab7.10.0环境下实现相关算法，完成基于图像连续表示的角点检测.当两直线段的夹角较小而直线段的灰度值较大时，易被误测为角点，同时当两条平行线靠得较近时也容易被误测出角点.为了去除这些伪角点，我们首先对检测出的所有直线进行筛选，去掉两条靠得较近的平行线中的一条；其次，给夹角设一个门限，若直线段夹角的正弦值的绝对值小于某一门限值时，则将其排除掉；最后，设置一个阈值，当两直线段的总灰度值相差太大时，即它们的比值大于预定阈值时，排除这些直线段.选取大小为256×256的人工图像和房子图像做实验，取夹角正弦值门限为0.5，总灰度值的比值阈值为0.01或100，用大津阈值法(OTSU)初步求得角点阈值，再运用最大角点响应函数值(阈值偏小时)或最小角点响应函数值(阈值偏大时)对所求得的阈值加权(权值为0.2～0.5)进行微调整，从而得到最终角点阈值.选取比周围3×3范围内T值(角点响应函数值)大并且大于角点阈值的点为角点.实验结果如图 2所示，其中图 2 (a)为人工图像和房子图像的原始图像，图 2 (b)为人工图像和房子图像基于梯度模的边缘检测图像，图 2 (c)为人工图像和房子图像经过角点响应函数处理后的图像，图 2 (d)为人工图像和房子图像的角点检测结果.

(a) 原图　　　　(b) 梯度边缘检测　　　(c) 角点响应函数效果　　　(d)角点检测图2　角点检测Fig.2　Corner detection

选取大小为256×256的人工图像作为实验对象，进行Harris经典角点检测算法与本文角点检测方法对比实验，对两种算法分别调整阈值使得角点检测效果达到最优，结果见图 3，其中图3(b)和图3(c)分别是Harris算法与本文算法在实验原图上的角点检测结果.这两种算法的角点检测性能对比情况见表 1(注：Harris算法所得的伪角点堆叠于真实角点附近).实验结果表明：利用数字图像连续表示方法进行角点检测可以得到不差于Harris经典角点检测算法的效果，而且正确率明显提高.

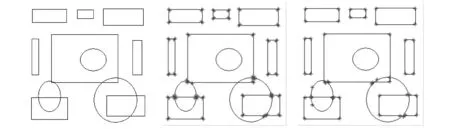
(a) 原图　　　　　　　　　　(b) Harris角点检测　　　　　　(c) 本文方法角点检测图3　本文方法角点检测与Harris角点检测Fig.3　The method of this paper and Harris corner detection

算法实际角点数/个检测出总角点数/个正确角点数/个伪角点数/个正确率/%Harris算法4099405940.40本文方法4052401276.92

为了验证本文角点检测方法对噪声的抗干扰性，我们对加了椒盐噪声的人工图像进行实验，结果如图 4所示，图 4(b)为加了椒盐噪声的人工图像，图 4(c)为本文方法对加了椒盐噪声的人工图像进行角点检测的结果，图 4(d)为Harris算法对加了椒盐噪声的人工图像进行角点检测的结果.实验结果表明：本文的角点检测方法可以有效克服噪声点对角点检测的干扰.

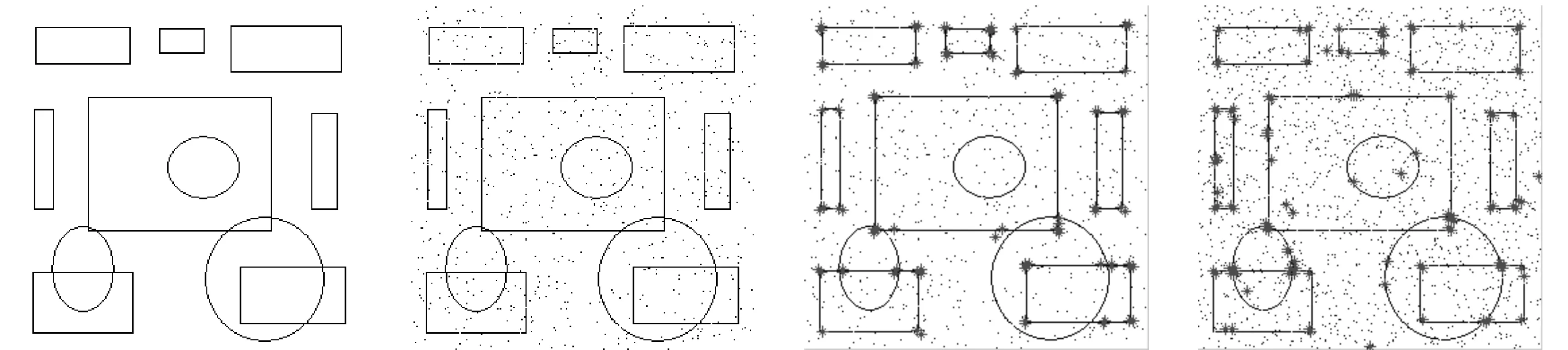
(a) 原图　　　　　　(b) 椒盐噪声图像　　　　　　(c) 本文方法　　　　　　(d) Harris算法图4　对噪声图像的角点检测Fig.4　The corner detection of noise image

通过上述实验，说明了利用数字图像连续表示方法处理离散图像可以得到不差于用传统离散图像处理方法处理的效果.本文运用基于数字图像连续表示的方法处理离散图像，对小矩形区域进行积分检测直线，进而根据角点响应函数实现对角点的检测，该角点检测方法可以有效克服噪声点对角点检测的干扰，对噪声具有较强的适应性.

参考文献

[1]CooperJ,KitchenL.Earlyjump-outcornerdetectors[J].IEEETransactionsonPAMI, 1993, 15: 823-828.

[2]HarrisC,StephensM.Acombinedcornerandedgedetector[C]//AVC.ProceedingsoftheFourthAlveyVisionConference,Manchester:UniversityofSheffieldPrintingUnit, 1988:147-151.

[3]AbdeljaouedY,EbrahimiT.Featurepointextractionusingscale-spacerepresentation[C]//IEEE.IEEEInternationalConferenceonImageProcessing(ICIP).Singapore:IEEE, 2004: 3053-3056.

[4]MokhtarianF,MohannaF.Performanceevaluationofcornerdetectorsusingconsistencyandaccuracymeasures[J].ComputerVisionandImageUnderstanding, 2006, 102: 81-94.

[5]RostenE,PorterR,DrummondT.Fasterandbetter:amachinelearningapproachtocornerdetection[J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 2010, 32(1): 105-119.

[6]BrobergP,RunnemalmA,SjödahlM.Improvedcornerdetectionbyultrasonictestingusingphaseanalysis[J].Ultrasonics, 2013, 53(2): 630-634.

[7]ShuiPL,ZhangWC.Cornerdetectionandclassificationusinganisotropicdirectionalderivativerepresentations[J].IEEETransactionsonImageProcessing, 2013, 22(8): 3204-3218.

[8]娄联堂，但威，陈佳骐. 数字图像连续表示及应用[J]. 中南民族大学学报(自然科学版)，2016，35(1): 136-140.

ContinuousRepresentationofImage-BasedCornerDetection

Lou Liantang, Wei Xiyu, Chen Jiaqi, Fang Zicheng

(CollegeofMathematicsandStatistics,South-CentralUniversityforNationalities,Wuhan430074,China)

AbstractThecornerdetectionmethodbasedoncontinuousrepresentationofdigitalimagewasstudiedinthispaper.Firstly,thecontinuousrepresentationofdiscretedigitalimagewasgivenbystringtheory,Fouriertransformwasusedtorealizethecontinuousrepresentationandreconstructionofdiscretedigitalimage.Then,thelinesegmentwasdetectedbydirectlycalculatingtheintegralofsmallrectangulararea.Next,theresponsefunctionofthecornerwasdefinedasthesizeoftheparallelquadrilateralarea,andthedetectionofcornerswasrealizedbyusingthedetecteddirectionallinesegment.Finally,thepropertyofthealgorithmwasanalyzedbyexperiments.Theapproachusedinthispaperisdifferentfromthetraditionalcornerdetectionmethodofthediscreteimage.Ithasstrongadaptabilitytothenoiseoftheimage.

Keywordscontinuousrepresentationofdigitalimage;linedetection;cornerdetection

收稿日期2016-03-03

作者简介娄联堂(1966-)，男，教授，博士，研究方向：数学应用方法与图像处理，E-mail:louliantang@163.com

基金项目国家自然科学基金资助项目(60975011)；中南民族大学中央高校基本科研业务费专项资金资助项目(CZW15051;YZZ13003)；中南民族大学研究生科研创新基金资助项目(2016sycxjj137)

中图分类号TP751.1

文献标识码A

文章编号1672-4321(2016)02-0151-06