让学生的创新思维自然流淌

洪建林

摘 要：数学学科的核心问题在于学生思维能力的发展，而创新思维又是学生思维能力的核心所在。创新思维本质上在于人具有活跃的状态、创造的自觉。让学生的创新思维自然流淌，有利于学生创新素质的发展，也有利于学生的可持续发展。当下，数学课堂教学务必追寻一种本真方法；综合运用、深度发散，自由自在地创新发展。

关键词：创新思维；自然流淌

数学学科的核心问题在于学生思维能力的发展，而创新思维又是学生思维能力的核心所在。创新思维是一种以新颖独创的方法解决问题的思维活动，这种思维能突破常规思维的界限，以超常规甚至反常规的方法、视角去思考问题，提出与众不同的解决方案，从而产生新颖、独到、有意义的思维成果，它具有变通性、独特性和敏感性等特性。怀特海认为，教育的全部目的就是使人具有活跃的思维。创新思维本质上在于人具有活跃的状态、创造的自觉。让学生的创新思维自然流淌，有利于学生创新素质的发展，也有利于学生的可持续发展。

当下，数学课堂教学务必追寻一种本真状态，让学生自主探索、灵活变通、合作对话、善于暴露、辨析比较、优化方法、综合运用、深度发散，自由自在地创造和发展。

一、自主探索，灵活变通——创新思维之“根”

怀特海认为，使知识充满活力而不是使之僵化，是一切教育的核心问题。即使一个简单知识点的教学，也会蕴涵内在的活力，这种活力更多来自学生的思维活动。因此，教师需要致力于让学生自主探索、独立思考。有了“独思”，学生才能充分挖掘自身潜能，不断变通思路，发展创新思维。

例如，教学苏教版小学数学五年级下册第13页例题9：

北京颐和园占地290公顷，其中水面面积大约是陆地面积的3倍。颐和园的陆地和水面面积大约各有多少公顷？

学生列方程解答后需要检验，教师鼓励学生从不同的角度进行。大部分学生列式72.5+217.5=290（公顷），也有部分学生列式：290-217.5=72.5（公顷）或290-72.5=217.5（公顷）。在接下来的检验中，有的学生用217.5÷72.5，看是否正好是3倍；有的学生用290除以72.5，看是否是4（即3+1）倍；还有的学生用217.5÷3，看是否等于陆地的面积……学生列出了不同的算式进行检验，角度不同、路径各异，展现了学生思维的创新性。

在这个例子中，我们发现并不是所有的学生都整齐划一地运用一种思路，他们没有做教材的奴隶，绝对“服从”教材提供的方法，即：72.5+217.5=290（公顷）；217.5÷72.5=3。学生在自主探索中从“我”出发，尊重“我”的思维取向，灵活运用加减法各部分之间的关系、乘除法各部分之间的关系变通思路，对“水面面积大约是陆地面积的3倍”有了灵活的理解，不拘泥于“水面面积÷陆地面积=3”这一模型，从而丰富了数学思维经验，对数量之间的整体理解比较深刻。可以看到，这样的思路变通富有价值、意义深远，对学生今后正确、灵活地检验，整体把握数量关系有着积极的作用。

不少教师在引领学生检验这一道题目时，往往是强化格式的规范性、模型的固定性，淡化了数学理解，抑制了学生的创造思维。只有让学生遵循自己的思路解决问题，立于“自我”，根于“自我”，变通思路、创新思维的过程才会有“根”。

二、合作对话，善于暴露——创新思维之“源”

学生创新思维的培养离不开合作，合作促进方法生成，合作促进深度思考，而课堂合作主要用对话进行。简单地说，对话是师生基于相互尊重、信任和平等的立场，通过言谈、倾听而进行的双向沟通、共同学习的过程，这是我们对“对话”的一个基本的定位。学生在对话中展露思维、发散思路，有效地促进了思维经验的积累。尤其是课堂上暴露的不同见解乃至差错，都是促进合作对话的良好资源，是创新思维之“源”。我们认为，任何一个学生的思考与挫折都应当视为精彩的表现来加以接纳。课堂上，即使生成了一些差错，只要教师正确对待，化腐朽为神奇，不仅不会影响课堂教学效果，还会激活学生的创造火花。

在教学苏教版五年级下册《解决问题的策略——一一列举》时，有这样的教学场景：

（1）出示“活动要求”。

活动一：尝试操作，感知策略

五（8）班种植小队在劳动实践基地“稚耕园”用22根1米长的木条围成一块长方形试验田，怎样围面积最大？

1.想一想：围成的长方形的周长一定是多少米？

2.画一画：下面每个小方格表示边长为1米的正方形，请你尝试画出不同的围法。（图略）

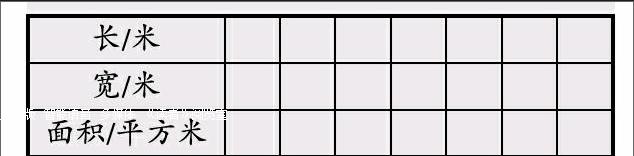
友情提醒：可以将不同长方形的长、宽等填在下面的表格中。

3. 组内交流：你是怎样围的？怎样围面积最大？

（2）学生进行操作、观察，教师巡视并进行适当的指导。

（3）各小组进行组内展示、交流，学生之间进行对话。

学生展示的研究情况多种多样，出现了以下的生成性资源：

……

针对以上不同的情况，学生进行了这样的对话：

生1：我认为表①中列举的情况不够齐全，少了长是8米、宽是3米。

生2：在列举时不能遗漏，要将符合条件的全部列举出来。

生3：少了一种情况后，面积最大的围法就可能不可靠。

生4：我觉得表②中列举到长6米、宽5米就可以了，后面的数据不需要列出来。

生5：是的，后面的两个图形已经出现，是重复的，不需要列举出来。

生6：表③的主要问题是数据排得有点杂乱，没有按照一定的顺序思考，不利于较快地解决问题。

……

（4）教师与学生对话、交流。

提问：我们可以借助列表进行列举，填表时可以从长（或宽）是几米的长方形开始想起？为什么要从长10米（或宽1米）的长方形开始想起？

生1：22÷2=11（米），周长的一半是11米，因为长、宽都是整米数，所以长最长是10米（或宽最短是1米）。

生2：从长是10米开始按照一定的顺序思考，接着依次是9米、8米、7米、6米。

生3：也可以从宽是1米开始按照一定的顺序思考，接着依次是2米、3米、4米、5米。

（5）学生观察、发现：一共有几种围法？长、宽各是多少米时，面积最大？你还有怎样的发现？

（6）师生谈话：刚才采用了列举的策略解决问题，我们是对不同围法一一列举，而且有顺序地进行思考，做到不重复、不遗漏，这样解决问题结果会更加可靠。（板书：有序思考 不重复 不遗漏）

钟启泉教授有这样的观点：教学不是告知与被告知的事情。教师上课的本质恰恰在于如何尊重学生的差异，尽可能地调动儿童活跃的思维，发现不同的思路，激活认知冲突，展开集体思维。在这一案例中，学生进行合作对话，出现了不同的思路，画出了不同的长方形，有的思考无序，有的出现遗漏，有的出现重复，不同的结果展现了不同的思维过程。在这原生态、接地气的思维暴露活动中，学生生成了各种各样的问题，在互动的过程中积累创造思维经验。在小组展示、对话过程中，学生结合数据进行补充、修正和完善，最后形成了一致的看法：通过一一列举，有顺序地进行思考，做到不重复、不遗漏，这样解决问题结果会更加可靠。可以说，整个对话过程充分暴露了学生的不同观点，展现了异中求同的创新思维过程。

三、辨析比较，优化方法——创新思维之“重”

郑毓信先生指出，相对于“善于举例”与“善于提问”而言，“善于比较与优化”应当说更为直接地涉及了数学学习的本质：这应该被看成一个文化继承的过程，且是在教师的指导下完成的，即主要表现为不断地优化。

以苏教版数学四年级下册《多边形的内角和》为例：

教师先复习了三角形的内角和及推导过程，接着出示了四边形、五边形和六边形等，引领学生提出不同的问题，有的学生提出：四边形的内角和是多少度？五边形呢？……还有学生提出：多边形的内角和可能与什么有关系呢？

学生通过合作交流，提出了这样的方法：

（1）用量角器量出每个角的度数，再求和；

（2）将四边形的四个角撕开，再拼在一起，看拼成的角可能是什么角？

（3）将四个角折一折，看组成的角是什么角？

（4）先尝试将四边形分一分，看可以分成几个已经学过的三角形？

……

这里，借助方法（1）（2），可以让学生动手操作，但这样的操作没有必要，从三角形的内角和推导看，学生已经发现：对于任意的三角形，如果每次都先测量、再求和（或将每一个角都撕下来，再拼一拼），比较麻烦，且测量容易产生误差，难以得到准确的结果。进而使学生明确：探索多边形的内角和，可以先将多边形分成若干个图形，分别求出每个图形的内角和，再相加。

在研究五边形时，学生出现了这样的方法：分成3个三角形（180°×3）或分成2个图形：1个三角形和1个四边形（180°+360°）。

在研究六边形时，学生的方法也很丰富：分成4个三角形（180°×4）；分成3个图形，即2个三角形和1个四边形（180°×2+360°）；分成2个图形，即2个四边形（360°×2）。

学生接着在小组内进行了这样的交流：

生1：研究四边形、五边形和六边形等图形时，可以通过分割的方法将多边形转化成已研究过的图形，再将各个图形内角的和相加。

生2：每一个多边形分割成已知图形的方法较多，似乎不容易发现规律。

生3：要是能将任意多边形分割成同一种图形，那该多好！

教师进行点拨：

怎样分割我们比较容易发现任意边数的多边形内角和的计算方法呢？能不能将各个多边形转化为比较简单的图形？

生4：可以把各个多边形分割成一定个数的三角形，再用三角形的内角和乘三角形的个数。

生5：三角形的个数等于多边形的边数减去2，所以多边形的内角和= 180°×（边数-2）。

生6：我觉得这样分割比较容易发现规律。

数学逻辑思维重在培养学生分析、比较、抽象和概括等方面的能力，而创新思维的重心也在于比较、优化，在辨析、比较等活动中进行异中求同、同中求异，对不同的思路、方法等进行优化选择和运用。在上面的案例中，随着边数的增加，学生感觉到分的方法越来越多，似乎难以发现规律，教师这时候进行画龙点睛，引领学生进行思维的变通：无论怎样分，我们都是将多边形通过分割的方法转化为已经研究的图形。怎样分割比较容易发现任意边数的多边形内角和的计算方法呢？学生的思维回归到解决问题的基点：分成一定个数的三角形比较容易发现规律，能够将多边形的边数与分成的三角形的个数建立一定的联系，从而构建解决问题的模型，优化解决问题的路径和方法。这样的教学既让学生发散思维，又让学生得到优化发展。

由此可见，在教学活动中教师必须有意识地让学生进行思路发散，同时组织学生辨析比较，在发散的基础上聚合思维，优化解决问题的思路，并寻求不同解决问题的方案，促进学生进行创新思维。

四、综合运用，深度发散——创新思维之“境”

不少心理学家认为，发散思维是创造性思维最主要的特点，是测定创造力的主要标志之一。结合生活实际，让学生综合运用已有的知识和经验，针对需要解决的问题提出不同的方案，对问题解决深度思考，能达成创新思维发展的新境界。

有这样的例子：教师结合生活实际，引领学生完成下列活动要求。

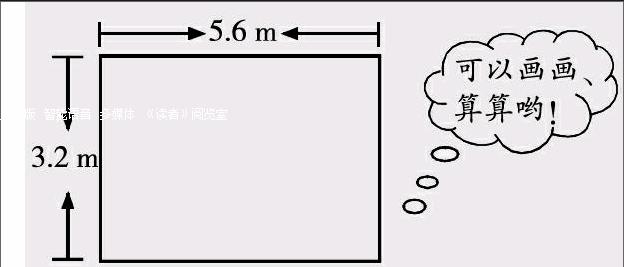
1. 一间长方形客厅，地面长5.6米，宽3.2米，用以下规格的方砖铺地：

价格表

瓷砖1规格：80 cm×80 cm，每块价格：90元；

瓷砖2规格：40 cm×40 cm，每块价格：25元；

瓷砖3规格：30 cm×20 cm，每块价格：10元。

活动：设计不同的方案

如果在客厅地面最外面一层正好铺满一种正方形瓷砖，里面正好铺满另一种瓷砖，可以怎样铺贴？

1. 组内分工合作，一人做好记录。

2. 我们小组的设计：最外面一层铺贴（ ）；里面铺贴（ ）。研究过程：

我们的研究结论：

3. 全班交流。

2. 学生分工合作，教师指导小组活动，注意对有困难的小组或学生进行点拨。

3. 师：请一个小组的同学汇报研究结果。

生1：最外面一层铺贴：80 cm×80 cm，里面铺贴：40 cm×40 cm，

（560-80×2）÷40=10（块），

（320-80×2）÷40=4（排），

560÷80×2+（320-80×2）÷80×2=18（块），

10×4×25+18×90=2620（元）。

生2：最外面一层铺贴：80 cm×80 cm，里面铺贴：30 cm×20 cm，

（560-80×2）×（320-80×2）÷（30×20），不是整数倍，里面不能正好铺满。

……

生3：最外面一层铺贴：40 cm×40 cm，里面铺贴：80 cm×80 cm，

（560-40×2）÷80=6（块），

（320-40×2）÷80=3（排），

560÷40×2+（320-40×2）÷40×2=40（块），

6×3×90+40×25=2620（元）。

生4：最外面一层铺贴：40 cm×40 cm，里面铺贴：30 cm×20 cm，

（560-40×2）÷30=16（块），

（320-40×2）÷20=12（排），

560÷40×2+（320-40×2）÷40×2=40（块），

12×16×10+40×25=2920（元）。

生4：有三种方案能让最外面、里面都正好铺满，其中两种方案的价格一样。

师：请生1说一说每一个列式求的是什么？

生1：（560-80×2）÷40求的是沿着里面的长铺贴，一排可以铺贴多少块； （320-80×2）÷40求的是沿着里面的宽铺贴，一排可以铺贴多少块（或者说：里面一共可以铺贴多少排？）；560÷80×2+（320-80×2）÷80×2求的是最外面一共可以铺贴多少块；10×4×25+18×90求的是一共要多少元。

师：请同学们在小组内交流不同算式表示的含义。

师：在不同的搭配方式中，关键是求出什么？

生：求出里面地面的长和宽，再看能不能正好铺满。

师：对于不同的可行性方案，可以先分别求出最外面和里面正好铺贴的块数，再计算出总价，看哪种比较合算。

以上案例表明，数学是思维的学科，实际问题的解决需要学生主动探索、积极思考。在不同的搭配方式中，关键是先求出里面地面的长和宽，再看能不能正好铺满。对于不同的方案，可以计算出总价，看哪种比较合算。这一活动具有丰富性、复杂性和严密性等特点，学生的活动经验在画画、算算、比比等操作、思考活动中愈加深刻。尤其是最外面一层铺贴正方形地砖后，里面可以怎样铺需要学生借助图示深度思考；由提出方案，到验证方案是否可行，再到得出结论，这样的过程是一个科学探究的过程，有利于学生掌握探究的方法。

总之，学生创新思维的发展，离不开教师精心的指导、组织和促进。教师只有不断引领学生自主探索、合作对话、比较优化、综合运用，让学生的创新思维在自然状态下尽情流淌，以培养创新思维为核心的素质教育才会绽放异彩。