ip-iq谐波检测法中数字低通环节的仿真研究

海　燕朱晓蒙

（1.安徽能源技术学校　安徽·合肥　230000；2.湖北工业大学电气工程学院　湖北·武汉　430068）



ip-iq谐波检测法中数字低通环节的仿真研究

海燕1朱晓蒙2

（1.安徽能源技术学校安徽·合肥230000；2.湖北工业大学电气工程学院湖北·武汉430068）

摘要：精确度与响应速度是衡量ip-iq谐波检测法性能的两个重要标志，因此对可影响ip-iq谐波检测法精度与响应速度的低通滤波环节进行研究。分别将常用的Ⅰ型切比雪夫、Ⅱ型切比雪夫、巴特沃斯三种数字滤波器用在ip-iq谐波检测法中的直流量提取环节，通过matlab进行了谐波检测的仿真试验。对三种低通方案的仿真结果进行详细的对比分析。得出结论：Ⅰ型切比雪夫低通滤波器可以使ip-iq谐波检测法具备较快的响应；巴特沃斯低通滤波器可使ip-iq谐波检测法在精度上具备优势，可根据精度、响应速度的需求对滤波器进行抉择。

关键词：ip-iq谐波检测；提取直流量；切比雪夫滤波器；巴特沃斯滤波器

1引言

有源电力滤波器（active power filter，APF）是一种可以动态跟踪电网谐波，且可对电网谐波进行高精度治理的电力设备［1］。从谐波含量较大的电网电流中精确、快速的分离出谐波指令电流成分是APF工作的先决条件［2］。基于瞬时无功功率理论的ip-iq谐波检测法为现阶段应用最为广泛的一种谐波提取方法［3］，此种谐波检测方案存在对有功及无功电流直流分量提取的环节，因此低通滤波器环节的设计与应用至关重要。提取谐波电流的精度、响应延迟时间与低通滤波器的通阻带幅频特性息息相关。相比于无限脉冲响应（infinite impulse response，IIR）滤波器，有限脉冲响应（finite impulse response，FIR）滤波器与IIR滤波器具有相同的滤波指标时，FIR滤波器的阶数要为IIR滤波器阶数的5～10倍才可满足要求［4］，成本高，延迟也长。因此本文采取数字IIR滤波器实现有功及无功电流分量的直流量提取，通过matlab/fdatool工具箱，对切比雪夫Ⅰ型、切比雪夫Ⅱ型、巴特沃斯三种最常用的数字IIR滤波器进行设计，然后分别用于提取ip、iq成分的直流量，进行matlab仿真，对比仿真试验结果对这几种低通滤波器实现ip-iq谐波检测法中直流量提取的优缺点进行研究。

2基于瞬时无功功率理论的ip-iq谐波检测法

基于瞬时无功功率理论的ip-iq谐波检测法，是应用非常广泛的一种谐波提取的技术。ip-iq全谐波检测的原理如图1所示。锁相环PLL对网侧电压进行锁相，发出与网侧电压同频的正余弦信号。三相负载电流iLa、iLb、iLc经3s-2s、2s-2r坐标变换得到ip-iq轴的有功及无功分量ip与iq，如式（1）。ip与iq通过低通滤波器（low pass filter，LPF），得到有功及无功电流的直流分量ip和iq，将ip和iq进行2r-2s、2s-3s坐标反变换，计算得到基波电流成分iaf、ibf、icf，如式（2）。最后用负载电流iaL、ibL、icL减去对应基波成分可到谐波电流iah、ibh、ich。

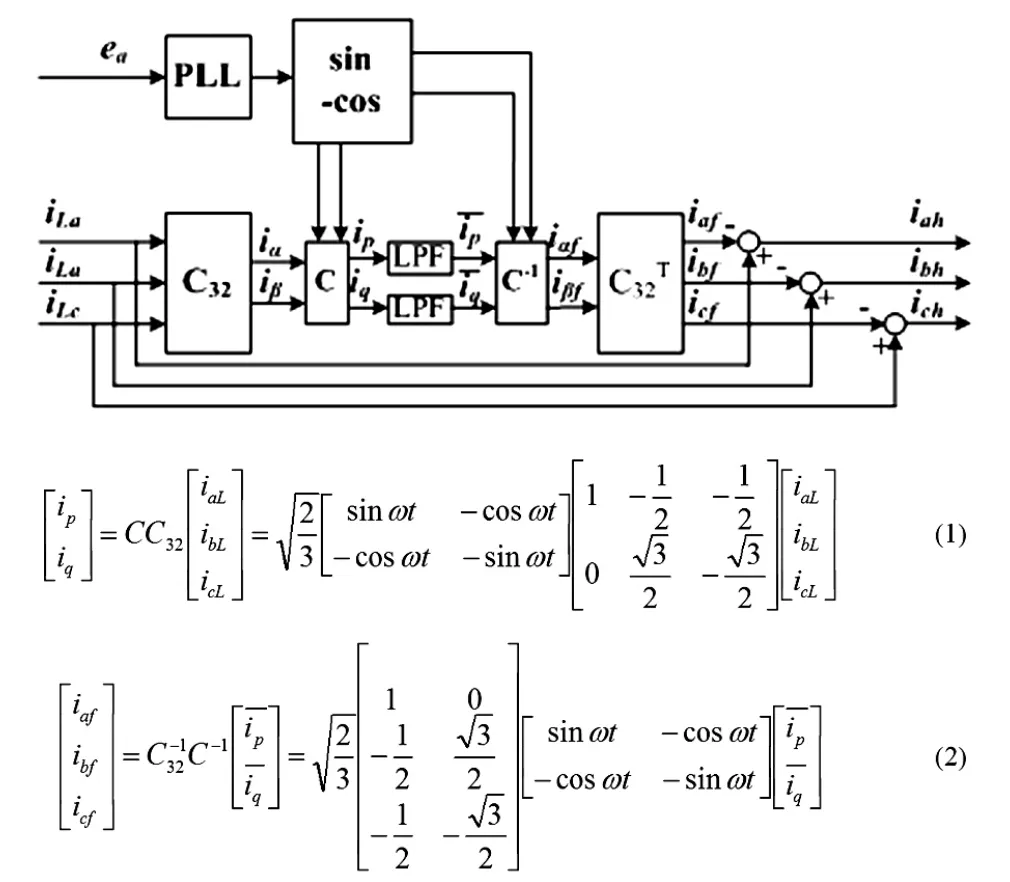
图1　基于瞬时无功功率理论的ip-iq谐波检测原理图

3低通滤波器的设计与分析

3.1切比雪夫Ⅰ型低通滤波器

切比雪夫滤波器具有在通频带或者阻频带内频率响应等波纹的特性［5］［6］，可以分为Ⅰ型切比雪夫滤波器和Ⅱ型切比雪夫滤波器。Ⅰ型切比雪夫滤波器的特点是其在通频带内具有等波纹的振幅，且在阻频带内的振幅特性是单调的。以下对Ⅰ型切比雪夫数字低通滤波器进行设计分析，综合考虑低通滤波器的性能与成本资源，本文所设计的所有低通滤波器皆为2阶的滤波器。用matlab/fdatool工具箱设计2阶Ⅰ型切比雪夫数字IIR低通滤波器：确定数字IIR切比雪夫Ⅰ型数字低通滤波器为2阶；设置信号采样频率Fs为10kHz；通频带的截止频率Fpass 为20Hz（本文所有低通滤波器截止频率都设置成20Hz）；鉴于通带最大衰减系数的绝对值越小，越有利于低频段信号的保真，对于低通滤波器来说是有利的，这里设置Ⅰ型切比雪夫低通滤波器的通频带截止频率处衰减指数Apass为0.1db小数值，要小于后面设计的巴特沃斯低通滤波器截止频率处3db的衰减指数。式（3）为设计的2阶Ⅰ型切比雪夫低通滤波器的传递函数H（z）。图2（a）为设计的2阶Ⅰ型切比雪夫低通滤波器的幅频响应特性曲线，可以明显看出，在通频带内，幅频对数曲线对应纵坐标值基本为0，说明在通频带内信号衰减很小，通带幅频特性良好，在阻频带的衰减系数下降较慢，导致大于截止频率的较低频率段信号的滤出效果可能不会特别理想。

图2　二阶切比雪夫低通滤波器的幅频响应特性曲线

3.2切比雪夫II型低通滤波器

II型切比雪夫滤波器的特点是其在阻频带内具有等波纹的振幅，且在通频带内的振幅特性是单调的。以下对II型切比雪夫数字低通滤波器进行设计分析。用matlab/fdatool工具箱设计2阶II型切比雪夫数字IIR低通滤波器：确定数字IIR切比雪夫II型数字低通滤波器为2阶；将信号采样频率Fs设置为10kHz；下阻频带的截止频率Fstop为20Hz；鉴于阻频带的衰减系数的绝对值越大，越有利于滤出高频段的信号，有利于实现低通滤波器，这里设置II型切比雪夫低通滤波器的阻频带衰减指数Astop为20db的较大数值，以便于较好的滤波性能。式（4）为设计的2阶II型切比雪夫低通滤波器的传递函数H（z）。图2 （b）为设计的2阶II型切比雪夫低通滤波器的幅频响应特性曲线，可看出，在大于截止频率的阻频带内的衰减指数下降较快；小于截止频率的通频带内，幅值衰减程度单调递增，5Hz～20Hz频率段衰减非常明显，可以说明低频信号失真会比较严重，通频带幅频特性差，可能会失去低通滤波的效果。

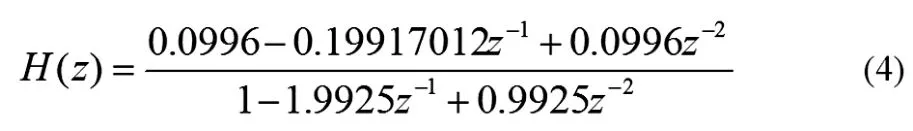
3.3巴特沃斯低通滤波器

巴特沃斯（Butterworth）滤波器是由英国的工程师Stephen Butterworth在其发表在《无线电工程》上的论文中最早提出的。在通频带中，Butterworth滤波器的幅频曲线可以达到最大限度的平滑［7］。在阻频带中，以某一临界频率开始，伴随频率的加大，对数幅频曲线的对数振幅单调下降，趋于负无穷。用matlab/fdatool工具箱对Butterworth数字IIR低通滤波器进行设计：首先确定滤波器的阶次为2阶；信号采样频率Fs仍设置为10kHz；截止频率Fc设置为20Hz；通频带截止频率处的衰减系数的绝对值固定为3db，此值明显大于前面设计的ChebyshevⅠ型低通滤波器的通带截止频率处的衰减指数。理论上通频带截止频率处的衰减指数越小，越有利于通频带内低频信号的保真。但由于butterworth滤波器通频带最大限度平坦的特性，且阻频带的振幅衰减系数下降速率相比于前面设计的Ⅰ型切比雪夫滤波器略快。因此，虽然butterworth低通滤波器通带截止频率处的衰减指数要大于设计的Ⅰ型切比雪夫低通滤波器，但butterworh低通滤波精度不一定就会低于Ⅰ型切比雪夫低通滤波器。式（5）为设计的二阶Butterworth低通滤波器的传递函数H（z）。图3为二阶巴特沃斯低通滤波器的幅频响应特性曲线，可以看出在通频带内，幅频曲线十分平坦，相比于本文设计的Ⅰ型切比雪夫低通滤波器的幅频特性曲线，此处设计的butterworth低通滤波器在阻频带的振幅衰减系数下降速率略占优势。

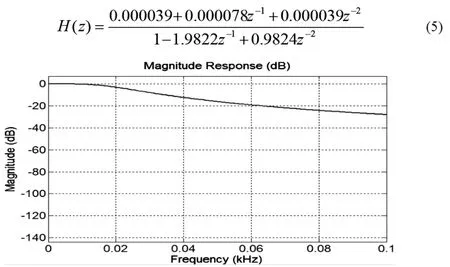
图3　二阶巴特沃斯低通滤波器的幅频响应特性曲线

4仿真研究

在matlab/simulink中搭建基于瞬时无功功率理论的ip-iq谐波检测仿真模型，包含三相电源模块、非线性谐波源模块、谐波电流检测模块。用带电阻负载的三相不可控整流桥来实现非线性谐波源，为观测提取谐波的动态响应性能，设置整流桥的负载电阻值于仿真时间0.1s处突增，0.2s处负载电阻值突减。图4给出了ip-iq谐波电流检测子模块的仿真模型。

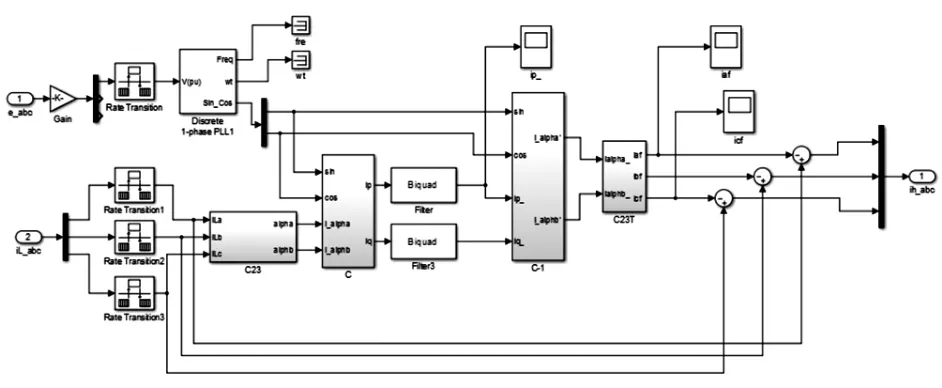
图4　ip-iq谐波电流检测子模块的仿真模型

主要仿真参数：网侧三相电压源的相电压有效值为220V，频率50Hz；不可控整流桥的电阻负载0.1s前为100欧，0.1s时电阻值突减为50欧，0.2s时电阻值再突增为100欧。谐波电流检测子模块中的采样频率设置为10kHz。仿真中，有功电流及无功电流成分的直流分量提取环节，分别采用前面设计的Ⅰ型切比雪夫低通滤波器、II型切比雪夫低通滤波器、巴特沃斯低通滤波器，分别将3种低通滤波方案成为方案1、方案2、方案3。

（1）方案1的仿真分析：图5（a）（b）为设计的Ⅰ型切比雪夫低通模式下，ip-iq谐波检测法提取的ip的直流量波形和A相基波电流波形。从ip成分的直流量可以看出，一个启动和两个负载突变阶段ip直流量提取的响应时间约在一个半工频（30ms）周期以内，响应速度比较快。对提取的A相基波电流进行FFT分析，波形在0.12s～0.14s的总谐波畸变率（total harmonic distortion，THD）为0.60％，0.22s～0.24s的THD为1.03％，畸变率都比较低，接近稳态下的THD，说明负载突变后，一个工频周期就快过渡到稳定提取谐波的状态，0.46s～0.48s的稳态段提取的A相基波电流THD为0.37％。

图5　方案1低通模式下提取的ip直流量与A相基波电流波形

（2）方案2的仿真分析：图6（a）（b）为设计的II型切比雪夫低通模式下，ip-iq谐波检测法提取的ip的直流量波形和A相基波电流波形。从ip成分的直流量可以看出，启动和两个负载突变阶段ip直流量提取的响应时间3个工频周期（60ms）以后，且波形存在明显的波动，说明响应速度与滤波精度都比较差。对提取的A相基波电流进行FFT分析，波形在0.12s～0.14s 的THD为4.82％，0.22s～0.24s的THD为4.46％，畸变率都比较高，且不接近稳态下的THD，说明ip成分的直流量提取响应速度确实比较慢，0.46s～0.48s的稳态段提取的A相基波电流THD为2.87％，高畸变率数值说明II型切比雪夫低通滤波器不适合用于ip-iq谐波检测法中的直流量提取环节。

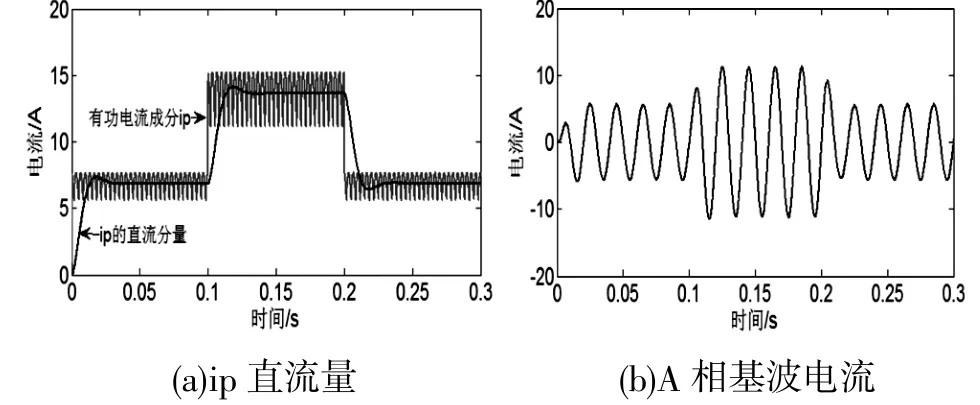
图6　方案2低通模式下提取的ip直流量与A相基波电流波形

（3）方案3的仿真分析：图7（a）（b）为设计的巴特沃斯低通模式下，ip-iq谐波检测法提取的ip的直流量波形和A相基波电流波形。从ip成分的直流量可以看出，启动和两个负载突变阶段ip直流量提取的响应时间约为两个多工频周期（40ms），响应速度相比Ⅰ型切比雪夫低通模式有所降低。对提取的A相基波电流进行FFT分析，波形在0.12s～0.14s的THD为1.04％，0.22s～0.24s的THD为2.05％，与稳态下的THD还有不小的差距，说明负载突变后，基波提取的响应速度确实不如Ⅰ型切比雪夫低通模式快，0.46s～0.48s的稳态段提取的A相基波电流THD为0.11％，对比Ⅰ型切比雪夫低通模式，基波提取的稳态精度有比较明显的优势，说明通频带最大限度平坦的特性和阻频带的振幅较快的衰减速率使基于巴特沃斯低通的ip-iq检测法有精度优势。图8为方案3低通模式下提取A相基波电流稳态频谱图。

图7　方案3低通模式下提取的ip直流量与A相基波电流波形

图8　方案3低通模式下提取A相基波电流稳态频谱图

结语

本文基于ip-iq谐波检测法中的有功及无功电流的直流量提取环节，设计了切比雪夫Ⅰ型、切比雪夫II型、巴特沃斯三种常用的数字IIR滤波器实现直流量提取，运用matlab做了对比仿真研究，得到结论：1）II型切比雪夫低通滤波器通频带内低频段衰减明显，低频信号失真比较严重，不适合用于ip-iq谐波检测法中的直流量提取环节；2）Ⅰ型切比雪夫低通滤波器可将通频带最大衰减指数压低，可使ip-iq谐波检测法中的直流量提取具备较快的响应；3）巴特沃斯低通滤波器通频带最大限度平坦的特性和阻频带的振幅较快的衰减速率，可使基于ip-iq检测法有精度优势。因此，若以精度为优先，可选butterworth低通滤波器，若以动态响应速度优先，可选Ⅰ型切比雪夫低通滤波器。

参考文献：

［1］吴峰，郑建勇，梅军等.并联有源滤波器PWM控制策略比较与实验分析［J］.电力系统及其自动化学报，2012，24（3）：53-58.

［2］陈明军，毛樟梅.改进窗函数在FIR数字滤波器设计中的应用［J］.继电器，2007，35（13）：65-67.

［3］叶佳明.基于瞬时无功功率理论的谐波和无功电流检测方法研究［D］.重庆：重庆大学，2012.

［4］王科.基于电压空间矢量双滞环电流控制的有源电力滤波器研究［D］.西安：西安理工大学，2014.

［5］王建行，姚齐国.基于MATLAB的切比雪夫低通滤波器设计［J］.新乡学院学报：自然科学版，2011，28（6）：531-533.

［6］郑光明.同轴腔对称广义切比雪夫滤波器研究［D］.成都：电子科技大学，2005.

［7］Upadhyay D K，Khanna T. Design and Analysis of Improved order Butterworth Lowpass Filters［C］. IEEE International Conferrence on CONECCT，2015：1-6.

［8］Fan M，Zhilong Z，Enjia W. The Design and Research of Generator Wave Filter Based on the APF and Zig-Zag Transformers［C］. IEEE International Conferrence on ICVES，2013：234-237.

中图分类号：TM761

文献标识码：A

文章编号：1009-8534（2016）03-107-03

作者简介：海燕，安徽能源技术学校，讲师，合肥工业大学硕士。