CFRP配筋高韧性复合材料正截面抗弯承载力研究
2016-07-13周小勇
袁 伟, 周小勇, 蔡 汗, 李 娜
(1.中国地质大学, 湖北 武汉 430074; 2.文华学院, 湖北 武汉 430074)
CFRP配筋高韧性复合材料正截面抗弯承载力研究
袁伟1, 周小勇1, 蔡汗1, 李娜2
(1.中国地质大学, 湖北 武汉430074;2.文华学院, 湖北 武汉430074)
摘要:尝试性的提出了CFRP配筋高韧性复合材料(CFRP-ECC)。依据工程水泥基复合材料(ECC)的单轴拉伸和压缩试验建立材料本构模型,提出基于平截面假定的CFRP-ECC正截面抗弯承载力计算理论,同时设计小梁试件进行四点弯曲试验,通过对比分析抗弯承载力理论值与试验实测值,验证计算理论的正确性。结果表明:提出的正截面抗弯承载力理论计算得到的结果与试验结果吻合很好,最大误差不超过4%,研究成果可供非金属配筋高韧性材料结构的计算分析提供参考。
关键词:CFRP配筋高韧性复合材料; 正截面; 抗弯承载力; 计算理论; 四点弯曲试验
0引言
传统钢筋混凝土构件在使用过程中因开裂后结构内部钢筋易受环境影响而锈蚀,易造成承载力的损失,最终导致耐久性差等问题。专家和学者为了解决这一问题,不断尝试用高性能材料代替钢筋的作用从而提高结构耐久性。CFRP[1]筋就是一种由碳纤维和基体组成的高性能碳纤维复合材料,其具有轻质、高强、耐腐蚀、耐疲劳等优点。将其代替钢筋作用于重要的混凝土构件中,可以较好的避免钢筋因锈蚀而产生的耐久性问题。
同时,近年来为国内外学者广泛关注的工程水泥基复合材料(Engineered Cementitious Composites,简称ECC)研究,提出了一种基于断裂力学、微观物理力学和统计学优化设计,使用短纤维增强,且纤维体积不超过总体积的2.5%,在拉伸荷载作用下,具有应变硬化和多裂缝开展的特征,拉伸应变可以稳定达到3%以上,材料试件表面最大裂缝宽度可以控制在100 μm以内的新型水泥基复合材料[2-4]。这种材料运用在混凝土结构中,可以减少主裂缝的产生与扩展,最大程度上避免结构失效,提高混凝土构件的耐久性。ECC在国内外的实际工程中已有成功应用的案例,如我国的港珠澳大桥和日本的横滨大厦等。
本文尝试性的将CFRP筋材和ECC的应用相结合提出了CFRP配筋高韧性复合材料(以下简称CFRP-ECC),并通过试验研究和理论推导,了解其协同工作的力学性能,为该材料在结构工程应用中的关键截面计算提供依据。由于CFRP筋材与普通钢筋力学特性不同,ECC与混凝土在本构关系上也有显著的区别,使得普通钢筋混凝土正截面受弯承载力计算方法已不适用于CFRP-ECC。本文依据ECC的单轴抗拉和抗压本构关系,结合CFRP筋的拉伸应力应变关系,提出了适用于CFRP-ECC结构的正截面抗弯承载力计算理论,同时设计CFRP-ECC试件进行四点弯曲试验,通过对比分析,验证计算理论的正确性。
1正截面抗弯承载力分析理论
1.1ECC的本构关系
依托于基金项目中对ECC材料的研究,通过试件的单轴拉伸和压缩试验得到的试验数据拟合出应力应变曲线(见图1),并以此得到了ECC材料的本构关系方程。

图1 ECC本构关系
1) 拉伸本构关系:
(1)
其中:εt0=0.001 8、εtp=0.060 6分别为开裂拉应变、极限拉应变;σt0=1.95 MPa、σtp=3.13 MPa分别为开裂拉应力、极限拉应力。
2) 压缩本构关系:
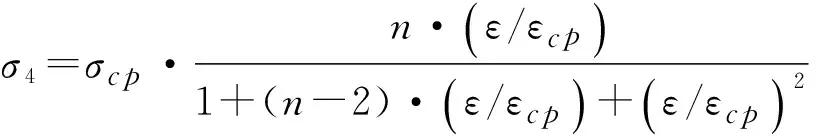
ε<0,n>0
(2)
其中:εcp=0.014为极限压应变;σcp=20 MPa为极限压应力,且n=2。
1.2正截面抗弯承载力计算理论
CFRP筋材没有屈服阶段,其合理的破坏应以抗压区ECC压碎为判断依据,此时CFRP筋材尚未达到极限抗拉强度,所以试件应按超筋设计[4]。伴随着截面下边缘拉应力的增加,整个抗弯过程CFRP筋应处于弹性阶段。且因ECC具有拉伸应变硬化的特点,所以在计算正截面抗弯承载力时构件下缘的拉应力是必须要考虑的。依据以上思路,可把CFRP-ECC正截面抗弯全过程分为3个阶段。
如图2,σs、As、Es分别为CFRP筋材的截面应力、截面面积和弹性模量;a为抗拉区应力转折点到截面抗拉区底部的距离;e为筋材中心距截面抗拉区底部距离;xc为中和轴高度。
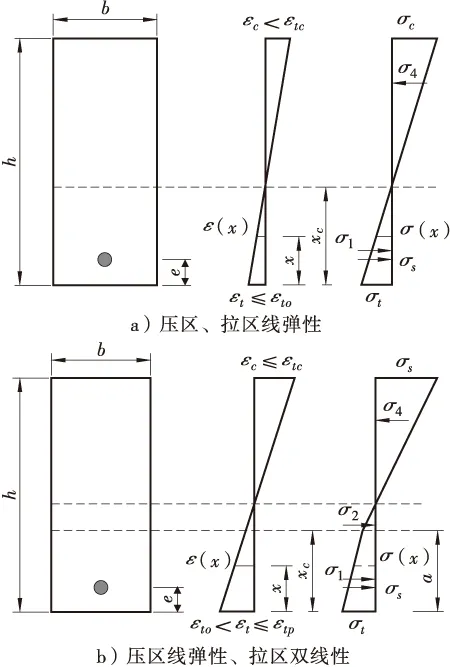
图2 不同阶段截面应力及应变分布
由平截面假定,以ECC底部拉应变εt为自变量,可得截面上任意一点的应变:
(3)
1) 弹性阶段(拉区、压区线弹性εt≤εto,εc<εcp):
在弹性阶段截面内力平衡方程组:
(4)
2) 弹塑性阶段(拉区双线性、压区线弹性εto<εt≤εtp,εc≤εcp):
在弹塑性阶段截面内力平衡方程组:
(5)
3) 破坏阶段(此阶段无计算公式,因εc>εcp,所以压区ECC破坏,构件失去承载力)。
2四点弯曲试验
2.1CFRP-ECC试件材料参数
CFRP-ECC的主要材料有CFRP筋、PVA纤维、水泥、粉煤灰、细砂、水、减水剂。水泥采用标号为42.5的普通硅酸盐水泥;Ⅱ级粉煤灰,45 μm方孔筛余量在12%~25%;砂为标准砂,经过筛分析试验得到,粒径控制在200 μm左右;试验采用桶装饮用水和聚羧酸高性能减水剂(中交二航武汉港湾新材料有限公司生产)。
1) CFRP筋
CFRP俗称碳纤维塑料筋,是结构上常用的筋材之一,与普通钢筋材料相比,具有强度高、密度小、耐久性好、非磁性、环保等优点。CFRP筋在拉伸荷载作用下的应力应变曲线呈线性关系,破坏前材料不会出现塑性性能。其性能指标见表1。
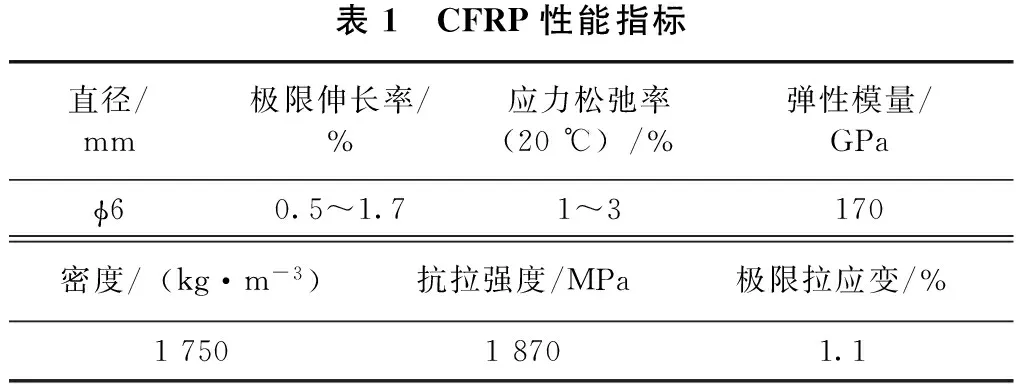
表1 CFRP性能指标直径/mm极限伸长率/%应力松弛率(20℃)/%弹性模量/GPaϕ60.5~1.71~3170密度/(kg·m-3)抗拉强度/MPa极限拉应变/%175018701.1
2) ECC
ECC指一种具有应变硬化特性和多缝开裂性能的高韧性复合材料,其由聚乙烯醇(polyvinyl alcohol,简称PVA)短切纤维、水泥、细砂、粉煤灰等组成,其中PVA纤维性能指标见表2。

表2 PVA纤维性能指标长度/mm直径/μm抗拉弹性模量/GPa密度/(g·cm-3)抗拉强度/MPa伸长率/%1239431.316207.0
2.2四点弯曲加载试验
为模拟梁构件在纯弯状态下,研究CFRP-ECC材料的力学性能,试验设计30 mm×50 mm×400 mm小梁试件,截面配筋率1.88%,截面及加载方式如图3;四点弯曲试验采用美国CMT5305型300 kN微机控制电子万能试验机,两点对称加载,试验加载过程如图4。
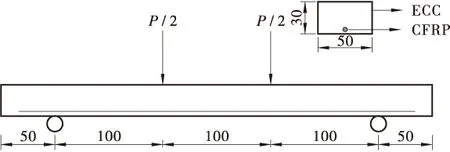
图3 试验加载及试件截面示意图(单位: mm)


a) 加载初期 b) 加载至破坏
2.3理论推导与试验结果分析
试件尺寸为30 mm×50 mm×400 mm,故h=30 mm,b=50 mm,加载部分长度l=300 mm;CFRP筋材直径φ6,中心距ECC抗拉底部距离e=8 mm。
2.3.1理论推导
(6)
令εt=εto,构件下缘达到开裂拉应变而即将开裂,代入数值得中和轴高度xc=11.95 mm,再代入式(4)中得开裂弯矩Mcr=25.47 N·m,开裂荷载Pcr=6M/l=509.47 N。
弹塑性阶段根据公式(1)、(2)、(3)、(5),可推得式(7):
(7)
令εc=εcp,构件上缘达到极限压应变而即将破坏,代入数值得中和轴高度xc=13.21 mm,再代入式(5)中得极限弯矩Mu=144.20 N·m,极限荷载Pu=6M/l=2 883.86 N。
2.3.2试验结果
通过试验加载最后得到的荷载时间曲线可以知道3个试件对应的初裂荷载和极限荷载,将理论计
算所得初裂荷载和极限荷载绘制在图5,可知其与试验值是比较接近的。
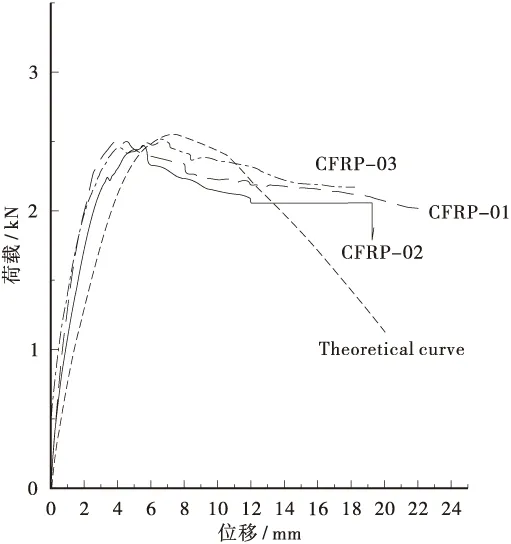
图5 试验荷载位移曲线及理论曲线对比
2.3.3误差分析
将3个试件试验所得值和计算理论值列于表3并进行误差分析。

表3 误差分析表荷载类型试验值/N试件一试件二试件三计算理论值/N误差/%试件一试件二试件三最大误差/%初裂荷载528520514509.473.552.091.013.55极限荷载2779278827812883.863.763.423.693.76
由上表分析结果可知,初裂荷载的理论计算值与试验实测值最大误差为3.55%,极限荷载的理论计算值与试验实测值最大误差为3.76%,均不超过4%。可见计算理论得到的数值与试验实测值比较吻合。
3结论
1) 对配CFRP-ECC提出的正截面抗弯承载力理论计算方法计算所得数值与四点弯曲试验结果吻合良好,验证了文章提出的基于平截面假定的CFRP配筋高韧性复合材料(CFRP-ECC)正截面抗弯承载力计算理论的正确性。
2) ECC具有拉伸应变硬化的特征,因此文章理论推导中考虑了ECC对受弯截面下缘抗拉能力的贡献,且经过计算其占整体拉力的16%~20%,可见在计算CFRP-ECC构件正截面抗弯承载力时ECC的抗拉是不可以忽略的。
3) 鉴于CFRP拉伸破坏前不会出现任何塑性,当结构采用CFRP配筋时建议按超筋来设计,研究成果可供非金属配筋高韧性材料结构的计算分析提供参考。
参考文献:
[1] P. J. Hefferman,M. A. Erki. Fatigue Behavior of Reinforced Concrete Beams Strengthened with Carbon Fiber Reinforced Plastic Laminates[J].J.Compos.Constr.,2004,4(3):132-140.
[2] Li V C.Advances in ECC research[J].ACI Special Publication on Concrete:Material Science to Applications,2002:373-400.
[3] Zhang J,Li V C,Andrzej S N,Wang S.Introducing ductile strip for durability enhancement of concrete slabs[J].Journal of Materials in Civil Engineering,2002,14(3):253-261.
[4] Li V C,Leung C K Y.Steady state and multiple cracking of short
random fiber composites[J].Journal of Engineering Mechanics,ASCE,1992,188(11):2246-2264.
[5] 高淑玲,徐世烺.PVA 纤维增强水泥基复合材料拉伸特性试验研究[J].混凝土与水泥制品,2007,47(3):233-239.
[6] 公成旭,张君.高韧性纤维增强水泥基复合材料的抗拉性能[J].水利学报,2008,39(3):361-366.
[7] 徐世烺,李贺东.超高韧性水泥基复合材料研究进展及其工程应用[J].土木工程学报,2008,41(6):45-60.
[8] Balaguru P.Contribution of fibers to crack reduction of cement composites during the initial and final setting period[J].Aci Materials Journal,1994(3):180-288.
[9] 杨帆.玄武岩纤维增强水泥基复合材料性能研究[D].武汉:武汉理工大学,2010.
[10] 孙明.不同纤维掺量及品种对ECC流变性能和弯曲性能的影响研究 [D].大连:沈阳建筑大学,2010.
[11] LI V C .From micromechanics to structural engineering The design of cementious composites for civil engineering applications[J].Journal of Structural Mechanics and Earthquake Engineering JSCE,1993,10(2):37-48.
[12] Marshall D B,Cox B N.AJ-integral method for calculating steady-state matrix-cracking stresses in composites[J].Mechanics of Materials,1988,7(2):127-133.
[13] 丁一宁,杨楠.玻璃纤维与聚丙烯纤维混凝土性能的对比试验[J].水利水电科技进展,2007(1):24-26.
文章编号:1008-844X(2016)02-0170-04
收稿日期:2016-01-18
基金项目:湖北省面上基金: 2013CFB187
作者简介:袁伟( 1991-) ,男,硕士研究生,研究方向: 土木工程
通讯作者:周小勇( 1978-) ,男,博士,硕士生导师,主要研究方向: 高性能复合材料及其工程应用,工程结构数值分析。
中图分类号:U 444
文献标识码:A
