极限分析和Monte-Carlo方法相结合的路基高边坡的局部可靠度和加固效果研究

揭光政

(湖南省高速公路管理局， 湖南 长沙　410001)



极限分析和Monte-Carlo方法相结合的路基高边坡的局部可靠度和加固效果研究

揭光政

(湖南省高速公路管理局， 湖南 长沙410001)

摘要：以蓝山湘江源至高塘坪公路段为工程背景，构建路基堆载土高边坡的局部稳定性状态分析模式。在借助极限分析方法获得边坡可靠度分析目标函数的基础上，结合Monte-Carlo法对该破坏模式下的边坡局部可靠度进行研究，实现了极限分析方法和Monte-Carlo法相结合的边坡可靠度分析方法。通过参数响应分析揭示各土体强度参数及其离散性对边坡稳定性和可靠度的影响规律。最后提出相应的边坡加固方法，并对加固效果进行数值模拟分析，以更好地服务于工程实际中。

关键词：路基; 堆载土高边坡; 局部可靠度状态； 数值模拟分析; 加固方法

边坡稳定性是岩土工程界的经典问题，传统的分析方法往往采用安全系数作为其评价指标，但是安全系数法无法将土体强度参数的随机性和离散性考虑在内，安全系数在可靠范围内但是边坡发生滑塌的现象时有发生[1,2]。在此种情况下，可对强度参数离散性和随机性进行考虑的边坡可靠度分析方法应运而生并在边坡稳定性评价中取得良好效果。

边坡可靠度分析方法往往需要与经典的边坡稳定性分析方法结合使用：极限平衡法在工程实际中应用十分广泛，但是其自身的假设条件过多，且求解过程过于复杂；有限元法是近年来兴起的边坡稳定性分析方法，具有灵活多变、适应性强等优点，但该方法无法获得边坡稳定性的界限值[3,4]；极限分析方法亦是边坡稳定性分析的经典方法之一，较之前两种分析方法，该方法的明显优点在于其可以给出边坡稳定性的一个明确界限值，即分别对应于上限法和下限法的上限解和下限解[5,10]，这一优点使其被工程界接受并被广泛使用。可靠度分析方法方面，目前已经开发出了较多种的可靠度分析方法，如一次二阶矩法[11]、响应面法[12]和Monte-Carlo法等，各种方法各具优劣，但其中Monte-Carlo法被认为是最具精确性的方法，因此也是应用最为广泛的可靠度分析方法[13-16]。

因此，本文在借助极限分析上限法构建的路基回填土高边坡滑动破坏模式的基础上，采用Monte-Carlo法对该边坡的局部稳定性和可靠度进行分析，通过参数响应分析获得各参数对上述两性质的影响规律分析，并最终提出行之有效的边坡加固方案，以方便工程施工。

1工程概况

本文所依托的路基填土高边坡工程的局部稳定性典型断面见图1，路基由原状土上进行部分土体堆载的方式构成。

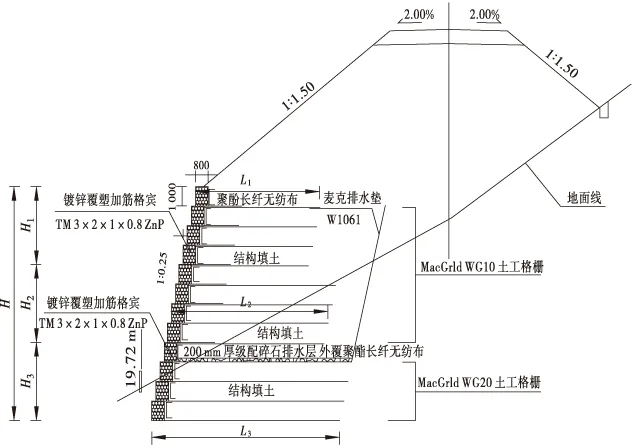
图1　路基边坡典型断面图

2破坏模式和能量计算

2.1破坏模式

图2　路基边坡局部破坏模式

采用极限分析上限法对边坡稳定性进行分析时，需要对破坏模式下的各项外力功率和内能耗散功率进行计算，并由各项能量耗散功率获得相应目标函数，下面分别对各项能量耗散功率进行计算。

2.2外力功率

外力功率由土体重力功率和地震力功率组成，且本文的破坏模式中，仅在曲边四边形ABDE上产生，上述两项外力功率分别采用叠加法和拟静力法计算，如下：

1) 重力功率：

WABDE=WOAE-WOAB-WOBD-WODE

(1)

2) 地震力功率：

(2)

其中，kh为地震力系数。

3) 该破坏模式下的土体外力功率：

W=Wγ+Wkh=

(3)

2.3内能耗散功率

1) 滑动面上的内能耗散功率:

(4)

2) 坡顶荷载功率:

边坡坡顶受到大小为q的均布行车荷载作用，该项功率所产生的内能耗散功率为：

(5)

3) 该破坏模式下的内能耗散功率：

Din=DAE+Dl

(6)

3可靠度分析目标函数

根据上文中对本文破坏模式下各项外力功率和内能耗散功率，令两者相等可以获得边坡可靠度分析的目标函数，即:

(7)

当破坏模式中的高度和角度参量满足条件：

(8)

4基于Monte-Carlo法的边坡可靠度计算

4.1基本原理

(9)

(10)

Monte-Carlo方法的基本原理是利用软件产生大量随机数，并将这些随机样本带入功能解析式中计算从而求出时间发生频率并得出结构可靠度的计算方法，即:

(11)

(12)

将随机事件总数N带入到上式中，即可得到目标函数R：

(13)

4.2边坡可靠度分析步骤

基于MATLAB软件的边坡可靠度计算步骤为：

1) 利用软件生成同均质和方差的随机数组；

5基于极限分析和Monte-Carlo法的边坡可靠度计算

在极限分析上限法获得的边坡可靠度目标函数的基础上，根据Monte-Carlo方法的基本原理，通过Monte-Carlo方法对边坡土体参数强度及离散性对边坡可靠度进行研究，实现极限分析方法与Monte-Carlo方法相结合的边坡可靠度分析。

5.1土体强度参数统计特性

以本文的工程背景为实例进行分析。经过原位测试得到该边坡土体的弹性模量E=7.5 MPa，泊松比μ=0.25，内摩擦角φ=5°，高度H=25 m，根据上述计算方法对边坡可靠度进行分析，其中边坡土体重度和黏聚力的统计特性如表1所示。

表1 土体参数统计表γ/(kN·m-3)c/(kN·m-2)均值标准差均值标准差2.780.43243.510.5478(对数正态分布)(对数正态分布) 注:括号内为参量分布特性。

根据上述统计结果，边坡可靠度为R=0.6879，发生滑坡的可能性较大，不能满足工程要求。

5.2土体强度参数敏感性分析

5.2.1设计图表

为对边坡土体统计参数对边坡可靠度进行分析，现分别在黏聚力φ=5°、10°、15°的情况下进行土体黏聚力c和重度γ的均质和变异系数对边坡可靠度影响的参数分析，其中图3a中黏聚力取值3.1 kPa到3.8 kPa，取值间隔0.1 kPa；图3b中重度取值2.5 kN/m3到3.3 kN/m3，取值间隔0.1 kN/m3；图3c和图3d中黏聚力变异系数和重度变异系数取值0到0.4，取值间隔0.05。

图3　边坡可靠度与粘聚力、重度、粘聚力变异系数、重度变异系数的关系

5.2.2结果分析

根据图3a、图3b、图3c认为： 土体粘聚力、重度和强度离散性对边坡可靠度具有明显影响，随着土体内摩擦角从5°上升到15°，各参数对可靠度的影响强度愈发明显，边坡可靠度随土体参数离散性的增大明显降低。

6数值模拟分析

为验证本文构建破坏模式及提出的加固方法的合理性，采用数值模拟分析软件对本依托工程边坡的潜在破坏和加固后边坡稳定性的状态进行分析。

6.1土工格栅加固的边坡数值模拟模型

本数值模拟模型中，采用土工格栅配合锚杆对路基堆载土高边坡进行加固，数值模拟模型效果图见图4。

图4　路基堆载高边坡加固模型图

6.2加固边坡的局部及整体稳定性分析

采用简化毕肖普法和简化简布法进行本次计算，其计算理论和我国的规范是一致的。Bishop法仅适用于圆弧滑动面，但实际工程中常常会遇到非圆弧滑动面的土坡稳定分析问题，如土坡下面有软弱夹层存在或者倾斜岩层面上的土坡，滑动面形状由于受到夹层或硬层的影响呈非圆弧的形状，此时采用圆弧滑动法分析就不太适用了，针对这种情况，采用Janbu折线法进行分析。

1) 局部稳定性分析。

局部稳定性计算模型的计算结果如图5所示，土工格栅配合锚杆加固后的边坡安全系数见表2。

a) TM 1

b) TM 2

2) 整体稳定性分析。

整体稳定性计算模型的计算结果如图6所示，土工格栅配合锚杆加固后的边坡安全系数见表2。

图6　路基堆载高边坡整体破坏模式

表2 路基堆载高边坡安全系数统计表计算工况正常工况计算值规范值TM1内部安全系数1.474TM2内部安全系数1.7521.25抗滑稳定安全系数2.5261.30抗倾覆稳定安全系数5.0851.50整体稳定安全系数1.4871.25

7结论

根据极限分析法获得的边坡可靠度目标函数，在此目标函数的基础上采用Monte-Carlo方法从土体强度统计参数和其离散性等不同角度对边坡可靠度的参数影响规律进行了分析，并采用数值模拟的手段对本文给出的边坡加固方法进行了验证。获得的主要结论如下：

1) 本文实现了极限分析上限法与Monte-Carlo法联合使用的边坡可靠度分析，由于获得的边坡可靠度为同等参数条件下的上限解。作为阀值，本文的计算结果较之无法获得限界解的传统可靠度分析

方法更具优势。

2) 根据本文的计算结果，当土体内摩擦角从5°增加到15°时，边坡可靠度随着黏聚力c和重度γ而变化的幅度从低于5%增大到30%以上，即对土体粘聚力和重度较低的土体，土体内摩擦角的变化对可靠度影响十分强烈。工程中应在控制土体黏聚力的基础上，选择增加土体内摩擦角的方法加固边坡。

3) 除增加土体内摩擦角外，本文亦对土工格栅加固坡面配合锚杆加固土体的方法进行了研究，并认为该方法亦对堆载土路基边坡局部和整体稳定性的提高具有积极作用，工程中可广泛使用。

参考文献：

[1] Jimenez-Rodriguez R, Sitar N, Chacón J. System reliability approach to rock slope stability[J]. International Journal of Rock Mechanics & Mining Sciences, 2006, 43(6):847-859.

[2] Jimenez-Rodriguez R, Sitar N. Rock Wedge Stability Analysis Using System Reliability Methods[J]. Rock Mechanics & Rock Engineering, 2007, 40(4):419-427.

[3] Farah K, Ltifi M, Hassis H. Reliability analysis of slope Stability using stochastic finite element method[J]. Procedia Engineering, 2011(10):1403-1408.

[4] 谭晓慧, 王建国, 刘新荣,等. 边坡稳定的有限元可靠度分析[J]. 重庆大学学报(自然科学版), 2006, 29(1):102-104.

[5] 王根龙, 伍法权, 门玉明. 基于土质边坡塑性极限分析条分法的可靠度计算方法研究[J]. 工程地质学报, 2006, 14(6):835-840.

[6] 孙平. 基于非相关联流动法则的三维边坡稳定极限分析[D]. 北京：中国水利水电科学研究院, 2005.

[7] 何叔航. 加筋二级边坡极限分析方法研究[J]. 公路工程, 2012, 37(3):89-91.

[8] Saada Z, Maghous S, Garnier D. Stability analysis of rock slopes subjected to seepage forces using the modified Hoek-Brown criterion[J]. International Journal of Rock Mechanics & Mining Sciences, 2012, 55(55):45-54.

[9] Li A J, Merifield R S, Lyamin A V. Limit analysis solutions for three dimensional undrained slopes[J]. Computers & Geotechnics, 2009, 36(8):1330-1351.

[10] Li A J, Lyamin A V, Merifield R S. Seismic rock slope stability charts based on limit analysis methods[J]. Computers & Geotechnics, 2009, 36(1，2):135-148.

[11] 李东升, 刘东升, 王渝昆. 煤矿区矸石山塑性极限可靠度分析[J]. 重庆大学学报(自然科学版), 2008, 31(12):1441-1445.

[12] Cho S E. First-order reliability analysis of slope considering multiple failure modes[J]. Engineering Geology, 2013, 154(3):98-105.

[13] Cho S E. Probabilistic stability analyses of slopes using the ANN-based response surface[J]. Computers & Geotechnics, 2009, 36(5):787-797.

[14] Papadrakakis M, Lagaros N D. Reliability-based structural optimization using neural networks and Monte Carlo simulation[J]. Computer Methods in Applied Mechanics & Engineering, 2002, 191(32):3491-3507.

[15] 袁景, 张秀丽. 基于Monte-Carlo方法的边坡可靠性分析[J]. 辽宁工程技术大学学报(自然科学版), 2005, 24(S2):10-12.

[16] 赵文斌, 罗文强, 冯永. 基于Monte-Carlo模拟的狮子包边坡稳定性研究[J]. 地质科技情报, 2006, 25(6):96-98.

文章编号：1008-844X(2016)02-0010-04

收稿日期:2016-03-24

作者简介:揭光政( 1985-) ，男，从事公路建设管理工作。

中图分类号：U 416.1

文献标识码：A