考虑碰撞效应的钢筋混凝土桥梁地震响应分析
2016-07-13龚燕轶
常 辉, 龚燕轶
(1.湖南明成达工程咨询有限公司, 湖南 长沙 410004; 2.湘西自治州交通建设工程造价管理站, 湖南 吉首 416000)
考虑碰撞效应的钢筋混凝土桥梁地震响应分析
常辉1, 龚燕轶2
(1.湖南明成达工程咨询有限公司, 湖南 长沙410004;2.湘西自治州交通建设工程造价管理站, 湖南 吉首416000)
摘要:在强震作用下桥梁结构往往由于过大位移而在梁体之间以及梁体和桥台之间发生碰撞。同时,钢筋混凝土桥墩可能进入了塑性范围。以一座两联多跨钢筋混凝土连续梁为例,分别建立考虑碰撞和不考虑碰撞有限元模型,同时考虑墩柱的非线性效应,并输入常用地震波进行非线性时程分析。研究结果表明,考虑碰撞效应以后,两联的主梁之间会产生巨大的碰撞力,从而相邻联间的相对位移有所增加,然而,墩底的弯矩和剪力却变化不大;同时考虑了桥墩的非线性效应以后,上部结构主梁间的相对位移有进一步的增加,因此,建议在钢筋混凝土桥梁的抗震设计中有必要同时考虑主梁碰撞效应和墩柱非线性效应。
关键词:桥梁工程; 地震; 碰撞效应; 非线性分析
0引言
桥梁作为交通运输生命线的重要组成部分,其抗震防灾越来越受到人们的关注。特别是,随着发生在城市中的几次地震的影响,桥梁工程界开始认真地对待桥梁碰撞问题,并逐步开始了大量的关注和研究。1976年,我国唐山发生了大地震,学者们就对一些桥梁的震害情况进行了调查和研究,并指出很多的落梁现象都是由于桥梁在地震作用下的碰撞导致的[1]。在1971年的圣费尔南多地震,一座高速公路桥梁的桥台处发生破坏,也是由于上部结构与桥台之间发生强烈的碰撞导致的[2];1989年的美国Loma Prieta地震中,位于旧金山市的一座高架桥的立柱发生剪切破坏,也是由于主梁位移超过预留空隙,与立柱发生碰撞导致的[3]。1995年,日本阪神大地震中,西宫港大桥的一联引桥发生落梁破坏现象,也是由于地震导致主梁与引梁之间的相对位移过大,超过了支承面的宽度[4]。在1999年的CHI-CHI大地震中,有近30座桥梁由于在伸缩缝发生了碰撞效应而导致了损伤。以上震害调查报告表明,强震来临时,桥梁容易发生较大位移,引起碰撞,导致支座失效、上部结构端部开裂、伸缩缝破坏等,严重时会发生落梁等严重灾害。
在地震作用下,影响桥梁碰撞效应的因素较多,例如,输入震波的选取、碰撞间隙或伸缩缝的大小、墩柱的非线性效应等[5]。对于影响桥梁碰撞的因素有哪些,一直是学者在研究地震碰撞作用中所关注的。Ruangrassamee等人[6]提出,通过考虑碰撞影响的相对位移反应谱,来考虑碰撞对相对位移的影响。DesRoches[5]等人的研究结果表明,结构的基本周期和地震波的卓越周期对桥梁的碰撞效应的影响非常大。近年来,国内也开始研究相邻主梁间碰撞对桥梁结构地震响应的影响。例如,同济大学的李建中等人通过对桥梁模型进行非线性动力时程分析,研究发现相邻联的基本振动周期是影响碰撞的主要因素[7]。谢旭等人在研究隔震简支梁间碰撞效应以后发现,碰撞不会导致落梁,其原因是碰撞主要是轴向迎面方向,使长周期联位移需求减少[8]。天津大学的岳福清[9]建立了桥梁碰撞分析的等效Kelvin碰撞模型及其参数确定方法和隔震梁桥地震碰撞临界间隙的计算方法。
本文针对强震时桥梁的碰撞反应进行分析,研究了碰撞效应和墩柱非线性效应对钢筋混凝土桥梁地震响应的影响。主要通过对一座两联连续梁在地震碰撞作用下的非线性时程分析,探讨了碰撞对桥梁的影响。本文研究结果表明,地震时桥梁的碰撞效应不可忽略,在今后的钢筋混凝土桥梁抗震设计中,有必要考虑桥墩的非线性以及相邻主梁之间碰撞效应的影响。
1算例桥梁有限元建模
本文选取的工程背景为一座由两联组成的多跨钢筋混凝土连续梁结构,其中,一联为3跨,另一联为2跨,每跨跨径均为30m,桥墩高均取为10 m。算例桥梁基本布置如图1所示,桥梁的上部结构采用C50混凝土,而桥墩采用C40混凝土。上部结构主梁和桥墩的截面特性如表1所示。本文采用SAP2000非线性有限元程序建立算例桥梁的有限元模型。
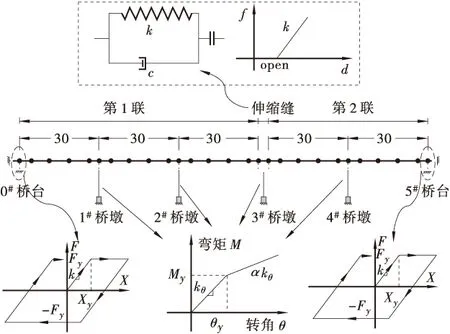
图1 算例桥梁计算模型(尺寸单位: m)
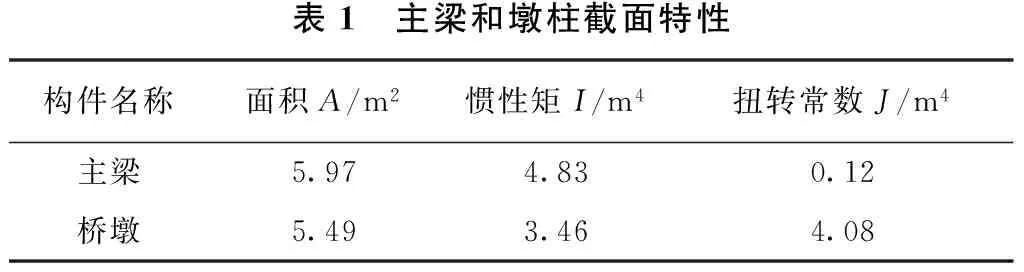
表1 主梁和墩柱截面特性构件名称面积A/m2惯性矩I/m4扭转常数J/m4主梁5.974.830.12桥墩5.493.464.08
在SAP2000程序中,伸缩缝可采用软件自带的碰撞单元来模拟桥梁的碰撞。本文采用Kelvin碰撞模型,如图1所示。图中,k为弹簧常数,c为阻尼系数。根据既往的研究成果提到的方法[9],在SAP2000程序中,可以取弹簧刚度定为6.3×108N/m,把粘滞阻尼单元的阻尼定为2.2×106Ns/m。
同理,对于桥台伸缩缝,在本文中取其单元刚度k取为3.955×106kN/m,单元缝隙取为0.08 m。另外,两岸桥台处的支座采用聚四氟乙烯滑板橡胶支座。在SAP2000程序中,支座的理想非线性模型如图1所示,根据我国2008《桥梁抗震设计细则》进行计算可得,支座模型弹性阶段的刚度为7.8×103kN/m,屈服力为397 kN,屈服后刚度比为0.002,屈服指数为10。
本文将1#~4#桥墩均分为4个节段,墩底节段被假定的塑性铰区域,长度为1.5 m。在SAP2000中可以采用刚体单元,并在刚体末端点处设置一非线性旋转弹簧(M-θ)来模拟墩柱塑性铰。M-θ弹簧的模型如图1所示,图中,My为屈服弯矩,θy为屈服角转度,α为屈服后刚度系数。可以假设塑性的曲率沿着塑性铰区域均一分配,然后采用数值积分法进行截面弯矩-曲率分析(考虑相应的轴力),得到截面弯矩-曲率曲线,然后再把实际的弯矩-曲率曲线等效为弹塑性双线性恢复力模型。
2地震波输入
本文采用非线性时程分析方法对算例桥梁进行分析,选取了常用的EL-Centro波和天津波作为模型的实际地震波输入,两条实测地震波的地震动信息如表2所示,为了更多的得到桥梁结构的地震非线性响应,即碰撞现象能够发生且墩柱能进入塑性。 本文将两条波的PGA统一调整为400 cm/s2。另外,本文主要考虑桥梁纵向的地震响应,因此忽略横向和竖向的地震波输入。

表2 输入的地震波信息地震名称记录时间峰值加速度/(cm·s-2)EL-Centro1940-05-08341.7天津1976-11-15105.6
3碰撞对桥梁地震响应结果的影响
根据前文中所建立的算例桥梁有限元动力分析模型以及所选取的地震波输入,采用SAP2000程序进行非线性时程分析。本文接下来将从以下两个方面分别进行比较分析。
3.1碰撞效应的比较结果
为了研究碰撞效应对桥梁结构动力响应的影响,首先,分别对考虑碰撞单元和不考虑碰撞单元的两种分析工况进行分析。其中,对于考虑了碰撞单元的工况,两联桥梁之间伸缩缝间距取为0.12 m。 图2为在相同的EL-Centro地震波激励下,考虑和不考虑碰撞时,碰撞单元处两联主梁的相对位移比较。由该图可以看出,考虑碰撞后两联主梁之间的相对位移明显增大,很容易导致落梁现象的发生。其相对位移最大数值的比较情况见表3所示。由此可见,在桥梁的抗震分析和抗震设计中,不能忽略桥梁各联之间的碰撞效应。
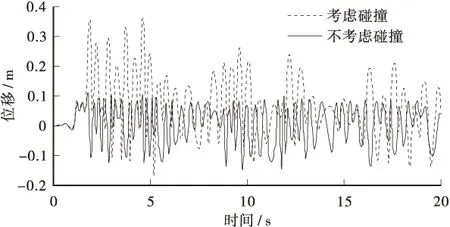
图2 碰撞单元处两联主梁的相对位移
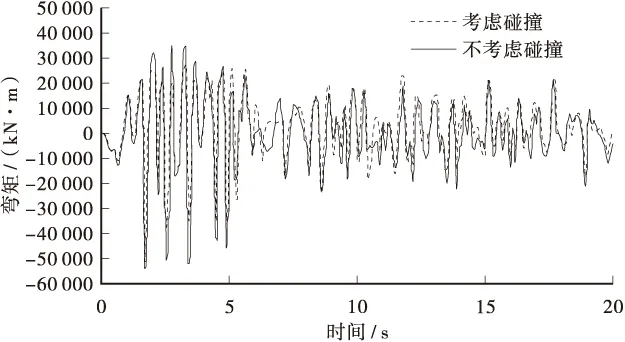
图3 碰撞单元处桥墩底弯矩
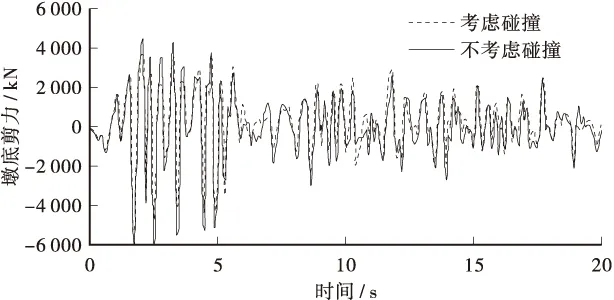
图4 碰撞单元处桥墩底剪力
另外,图3和图4分别是碰撞单元处混凝土桥墩的墩底弯矩和剪力时程响应的比较情况。由这两个图中可以看出,考虑了碰撞效应以后,桥墩的墩底剪力和弯矩都略有增加,但增加效应并不十分明显,这说明分析中考虑碰撞与否对墩底弯矩和剪力影响较小。
3.2同时考虑碰撞与墩柱非线性的比较结果
钢筋混凝土桥梁结构在强震作用下,桥墩很容易进入非线性,从而导致结构整体刚度减小,结构周期变长,进而导致桥梁结构的位移有所增大。因此,桥墩的非线性效应,也是影响桥梁结构碰撞的一个重要因素。因此,为了研究墩柱非线性效应的影响,本节在考虑相同碰撞效应的前面下,又分两种工况进行对比分析,一种工况是考虑墩柱非线性;另一种工况是不考虑墩柱非线性,即采用弹性梁单元模拟墩柱。同时,在输入相同EL-Centro地震波作用的情况下,两种工况得到的主梁相对位移、墩底弯矩和墩底剪力时程响应曲线的比较结果,分别如图5~图7所示。
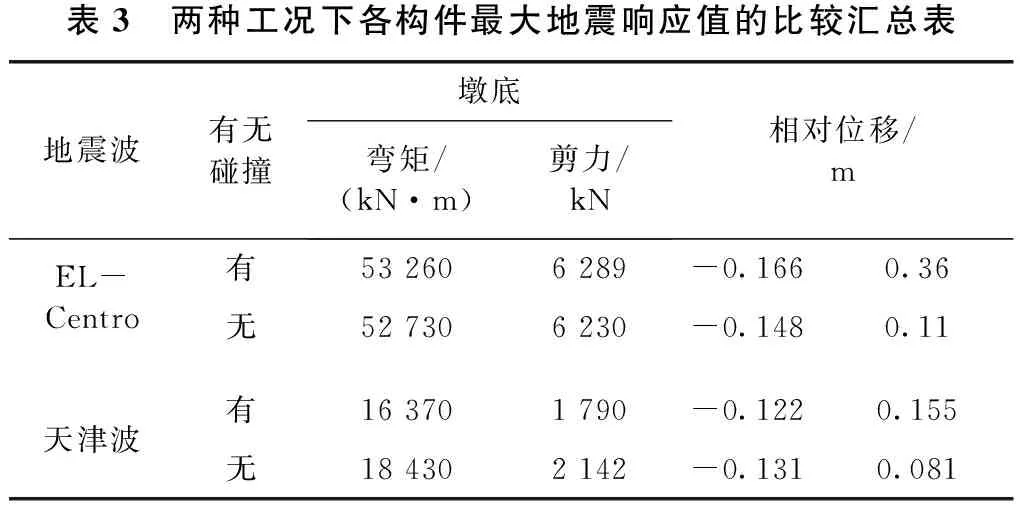
表3 两种工况下各构件最大地震响应值的比较汇总表地震波有无碰撞墩底弯矩/(kN·m)剪力/kN相对位移/mEL-Centro有532606289-0.1660.36无527306230-0.1480.11天津波有163701790-0.1220.155无184302142-0.1310.081
由图5可以看出,在考虑桥墩非线性效应以后,相邻主梁间的相对位移增加较明显,尤其是反方向的最大位移。由图6和图7可知,考虑桥墩非线性效应以后,墩底弯矩和剪力明显降低。这是由于,在考虑桥墩的非线性效应后,桥墩构件在有效刚度有所减少,从而导致相对位移的增大,进一步加剧了上部结构主梁之间的碰撞,同时降低了墩底弯矩和剪力。由此可见,如果在桥梁抗震分析与抗震设计中,忽略桥墩的非线性,很容易造成低估了桥梁的相对位移,导致地震发生时会产生落梁破坏。
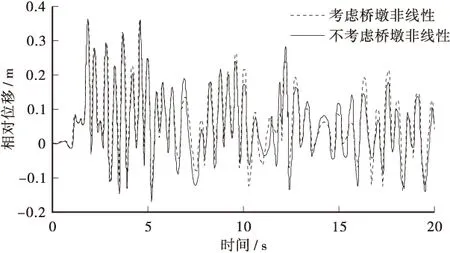
图5 墩柱非线性对碰撞单元处主梁相对位移的影响
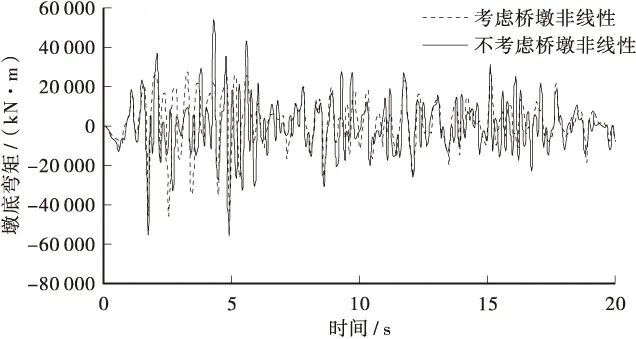
图6 墩柱非线性对碰撞单元处桥墩底弯矩的影响
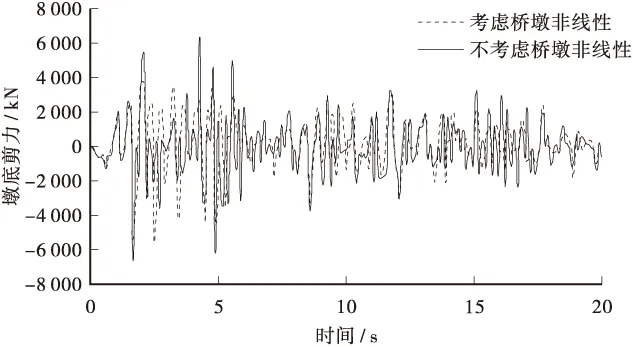
图7 墩柱非线性对碰撞单元处桥墩底剪力的影响
4结论
本文以一座常见的两联多跨钢筋混凝土连续梁桥为例,基于SAP2000非线性分析程序建立有限元模型进行非线性时程分析,研究了碰撞效应和墩柱非线性效应对钢筋混凝土桥梁地震响应的影响,主要得到以下结论:
1) 在强地震作用下,考虑了碰撞效应以后,尽管桥墩的内力变化不大,但相邻主梁间的相对位移明显增加,可能会导致落梁破坏,因此,在桥梁抗震设计中不能忽略碰撞效应。
2) 考虑桥墩的非线性效应后,桥墩构件在有效刚度有所减少,导致主梁相对位移的增大,进一步增加落梁破坏的可能性。因此,有必要同时考虑桥墩非线性以及相邻主梁之间碰撞效应的影响。
3) 建议在今后的钢筋混凝土桥梁抗震设计中,能够尽量准备模拟主梁间的碰撞效应和墩墩的非线性效应,从而减小地震导致的桥梁破坏。
参考文献:
[1] 范立础.桥梁抗震[M].上海:同济大学出版社,1997.
[2] Priestley M,Seible F and Galvi G.Seismic Design and Retrofit of Bridge[M].CE Press,1996.
[3] Kasai K,Maison B.Observation of Structural Pounding Damage from the 1989 Loma Prieta Earthquake[C].In:The Sixth Canada Conference of Earthquake Engineering,Toronto,1990.
[4] Park R.The Hyogo-Ken Nanbu Earthquake of 17 January 1995,Bull.New Zealand Nat[J].Soc.Earthquake Engineering,1995,28(1):43-44.
[5] DesRoches R and Susendar Muthukumar.Effect of pounding and restrainers on seismic response of multi-pule-frame bridges[J].Journal of Structural Engineering,2002,7(1):860-869.
[6] Ruangrassamee A,Kawashima K.Relative displacement response spectra with pounding effect[J].Earthquake Engineering and Structural Dynamics,2010,30(10):1511-1538.
[7] 李建中,范立础.非规则梁桥纵向地震反应及碰撞效应[J].土木工程学报,2005,13(1):84-90.
[8] 谢旭,高博青,吴善幸,等.柔性橡胶支座上的桥梁结构地震碰撞响应分析[J].浙江大学学报(工学版),2004,22(6):725-730.
[9] 岳福青.地震作用下隔震高架桥梁的碰撞反应及控制[D].天津:天津大学,2007.
文章编号:1008-844X(2016)02-0147-04
收稿日期:2016-03-01
作者简介:常辉( 1975-) ,男,工程师,主要从事工程咨询。
中图分类号:U 441
文献标识码:A
