融合RTS平滑的迭代无迹卡尔曼粒子滤波方法

李　敏，陈志梅，邵雪卷

(太原科技大学电子信息工程学院，太原 030024)



融合RTS平滑的迭代无迹卡尔曼粒子滤波方法

李敏，陈志梅，邵雪卷

(太原科技大学电子信息工程学院，太原 030024)

摘要：对粒子滤波算法中建议分布函数的设计提出了一种新的方法，即将迭代无迹卡尔曼滤波(Iterated Unscented Kalman Filtering，IUKF)与Rauch-Tung-Striebel(RTS)平滑算法融合，产生新的建议分布函数，以减小粒子滤波的粒子数匮乏现象，与单独使用无迹卡尔曼滤波产生建议分布函数的粒子滤波方法(Unscented Kalman Particle Filtering，UPF)相比，状态的估计结果更加准确，系统具有更好的稳定性。最后通过仿真研究验证了该方法的有效性。

关键词：粒子滤波；RTS平滑；状态估计

粒子滤波算法(Particle Filtering，PF)是用一组粒子来近似表示系统的后验概率分布，通过使用这一近似的表示来估计非线性系统的状态[1]，应用于多个领域[2]。这种方法实现起来简单，但是系统的最新测量值这一重要因素并没有在预测样本的考虑中，就会导致所抽取的样本与从系统真实状态后验概率分布的样本存在较大偏差，特别是当观测精度较高时，这种偏差特别明显，就会使滤波性能下降甚至发散，PF陷入困境[3-4]。许多学者已经从将最新的量测信息引入的角度出发来设计建议分布函数，提出了基于EKF、UKF等滤波技术的粒子滤波算法[5-7]。但当系统的非线性特性较强时，这类方法就会忽略了较大的积累线性化误差，导致算法的滤波性能下降。RTS平滑算法是由Rauch等在KF算法的基础上提出的[8]，是一种简单有效的平滑算法。

为了能够更加充分的利用观测信息，进而提高PF状态估计的精度，而且为使RTS平滑算法能适应于非线性系统，本文将IUKF与RTS平滑算法融合，设计新的建议分布函数，即先用IUKF对系统状态进行后验概率估计，然后用RTS平滑算法对滤波结果进行修正。从而减小了粒子滤波的粒子数匮乏现象，也使得状态的估计结果更加精确。

1RTS-IUKF-PF的设计

取如下非线性系统:

xk=f(xk-1)+ek

(1)

zk=h(xk)+vk

(2)

其中(1)为状态方程，(2)为观测方程。xk是tk时刻的n×1的状态向量；zk是tk时刻系统的m×1的观测向量；f(xk)∶Rn→Rn，h(xk)∶Rn→Rn为可微的非线性函数；ek是n维的过程噪声序列；vk是m维的量测噪声序列。两噪声序列的特性假定如下:

其中Qk是ek的n×n对称非负定协方差矩阵；Rk是vk的m×m对称正定协方差矩阵；δkj为克罗尼克(Kronecker)函数，满足δkj=1，δkj=0(k≠j).在此文中，认为系统的初始状态、系统噪声、量测噪声是互相独立的。

1.1粒子滤波算法的基本步骤

粒子滤波算法的基础是递推贝叶斯估计，可用于以状态空间模型描述的非线性系统。粒子滤波算法的基本步骤为：

基本粒子滤波算法中存在的最普遍问题就是粒子数匮乏现象[9-10]，即粒子逐渐丧失了多样性。设计合适的建议分布函数对于解决此问题是最为有效。最优的建议分布函数能将系统最新的观测信息考虑其中并且可以使重要性权值方差最小化。因此，本文提出了基于RTS-IUKF平滑设计新的建议分布函数，其具体设计步骤如下。

1.2RTS-IUKF平滑算法

基于IUKF算法的RTS平滑算法设计如下：首先在时间区间[0,N]内对前文非线性系统进行IUKF，过程为下面的①～⑤，然后再对滤波的结果进行RTS平滑修正，从而得到建议分布函数。

①sigma点的产生(比例修正UT)

(1)

i=1,…,n

(2)

i=n+1,…,2n

(3)

(4)

(5)

0其中n是状态向量的维数；λ=α2(n+κ)-n，κ是比例因数，当n>3，一般设为0；在n<3时设为3-n；α调节aigma点集与状态均值的距离，通常取一小正数，如1×10-4≤α≤1；β是非负的加权参数，包含分布的高阶矩信息，对高斯分布，2为最优值；χ为增广后的状态向量(sigma点)；P为状态协方差矩阵；w为sigma点的权值。

②通过状态方程xk+1=f(xk)+ek传递sigma点。

(6)

(7)

(8)

(9)

式中，qr{}表示矩阵的QR分解；cholupdate{}表示矩阵Cholesky分解的秩1修正。

④通过方程(2)zk=h(xk)+vk传递sigma点得到量测预测。

(10)

⑤利用迭代卡尔曼滤波(IKF)的思想估计预测量测的均值、协方差。

(11)

(12)

(13)

(14)

Sk,i=chol{Pj,i},Pk,i=Sk,i(Sk,i)T

(15)

⑥RTS平滑更新

(16)

(17)

Psk=Pk,i-Ksk(P0,i-Psk+1)(Ksk)T

(18)

1.3RTS-IUKF-PF算法

RTS-IUKF-PF算法步骤如下：

①初始化

②预测修正

<2>计算样本各点的权值：

③状态估计

2仿真算例与分析

通过仿真来说明建议分布函数的选择不同，对粒子滤波方法估计性能的效果就会不同。选择文献[11]中非线性高斯噪声模型进行仿真。分别采用PF、UPF、RTS-IUKF-PF三种算法对此模型进行状态估计。该模型的状态方程、观测方程分别为:

其中初始状x0态服从高斯分布x0～N(0,5)；wk是方差为10.0，均值为0的高斯白噪声，vk是方差为1.0，均值为0的高斯白噪声。

粒子数目为N=500个，观测时间为WT=50 s，采样间隔为5 s.UT的参数设置为α=1,κ=2.仿真结果如图1-3所示。

图1　PF、UPF、RTS-IUKF-PF的状态估计

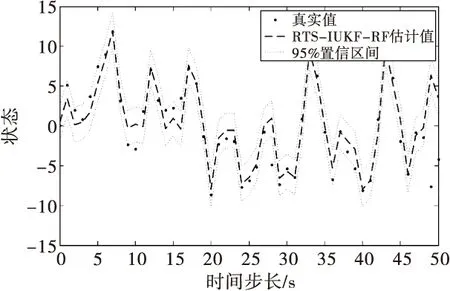
图2　本文算法落在95%置信区间

图3　PF、UPF、RTS-IUKF-PF的状态估计误差

滤波算法PFUPFRTS-IUKF-PF均方误差均值10.11647.00934.4326均方误差方差5.98361.87720.6459

从仿真结果可知，RTS-IUKF-PF对于状态估计的准确性极高，估计误差是最小的，明显优于UPF和PF.

3结论

建议分布函数的合理选择与粒子滤波的性能有着紧密的联系，本文中引入迭代策略和平滑修正使得RTS-IUKF建议分布能够更加充分的利用系统观测信息，所设计的新的建议分布函数使采样粒子更加符合系统状态的真实后验概率分布，从而提高了粒子滤波的估计性能。

参考文献：

[1]王法胜，鲁明羽，赵清杰，等.粒子滤波算法[J].计算学报，2014，37(8)：1679-1694.

[2]冯爱丽，乔钢柱，曾建潮.基于信标节点间距离的改进RSSI定位算法[J].太原科技大学学报，2012，33(1)：6-9.

[3]郭晓松，李奕芃，郭君斌.粒子滤波算法及其应用研究[J].计算机工程与设计，2009，30(9)：2264-2266.

[4]胡士强，敬忠良.粒子滤波算法综述[J].控制与决策，2005(4)：361-365.

[5]SZOTTKA I，BUTENUTH M.Advanced Particle Filtering for Airborne Vehicle Tracking in Urban Areas[J].Geoscience & Remote Sensing Letters，IEEE，2014，11(3)：686-690.

[6]程水英，余莉.迭代无味卡尔曼滤波器的算法实现与应用评价[J].系统工程与电子技术，2011，33(11)：2546-2553.

[7]郭平平，贾建芳.基于IUKF的非线性状态估计[J].机械工程与自动化，2010(5)：7-9.

[8]陈金广，高新波.基于分段RTS平滑的凸组合航迹融合算法[J].计算机科学，2010，37(4)：175-178.

[9]ADALI T，HAYKIN S.Adaptive Signal Processing：Next Generation Solutions[C]∥John Wiley&Sons，IEEE Press，2010：271-331.

[10]TAFTI A D，SADATI N.Novel adaptive Kalman filtering and fuzzy track fusion approach for real time applications[C]∥Industrial Electronics and Applications，2008.ICIEA 2008.3rd IEEE Conference on.IEEE，2008：120-125.

[11]KITAGAWA G.Monte Carlo Filter and Smoother for Non-Gaussian Nonlinear State Space Models[J].Journal of Computational & Graphical Statistics，2012，5(1)：1-25.

Iterated Unscented Kalman Particle Filter of Fusion RTS Smoothing

LI Min，CHEN Zhi-mei，SHAO Xue-juan

(Institute of Electronic Information Engineering，Taiyuan University of Science and Technology，Taiyuan 030024，China)

Abstract：This paper proposed a new proposal distribution function for the particle filtering，the Iterated Unscented Kalman Filter and the RTS smoothing are fused to generate the proposal distribution function so as to reduce the phenomenon of particle′s shortage.Compared with the particle filtering with only the proposal distribution function of Unscented Kalman Filter，this method can get more accurate estimation results and the system has more stability.Finally，the simulation results proved the effectiveness of the proposed method.

Key words：particle filtering，RTS smoothing，state estimation

收稿日期：2015-09-29

基金项目：山西省自然科学基金(2014011020-2，2014011020-1)

作者简介：李敏(1990-)女，硕士研究生，主要研究方向为智能检测技术及应用；通信作者：陈志梅，E-mail：zhimeichen400@163.com

文章编号：1673-2057(2016)04-0266-04

中图分类号：TP202

文献标志码：A

doi：10.3969/j.issn.1673-2057.2016.04.004