基于稀疏优化的织物疵点检测算法
2016-07-12刘洲峰李春雷
刘洲峰, 闫 磊, 李春雷, 董 燕, 李 阳
(中原工学院 电子信息学院, 河南 郑州 451191)
基于稀疏优化的织物疵点检测算法
刘洲峰, 闫 磊, 李春雷, 董 燕, 李 阳
(中原工学院 电子信息学院, 河南 郑州 451191)
为提高稀疏表示方法对织物疵点的检测精度,提出了基于稀疏优化的织物疵点检测算法。首先,利用L1范数最小化从待检织物图像中学习出自适应字典库,用该库对织物图像稀疏表示,进而计算出稀疏表示系数矩阵;然后,对系数矩阵进行优化处理,采用字典库及优化系数矩阵对织物图像稀疏重构;最后,将重构图像与待检织物图像相减生成残差图像,用最大熵阈值方法对残差图像分割,定位出疵点区域。实验结果表明,本文算法所重构图像准确表示了正常织物纹理,相比已有检测方法具有较高的疵点检测精度。
L1范数; 稀疏表示; 织物图像; 疵点检测
织物疵点检测是纺织品质量控制和管理的一个关键环节,对织物疵点检测与判别算法进行研究具有重要的理论意义与应用价值。已有疵点检测方法分为特征提取和非特征提取2类[1-3]。特征提取方法从织物图像的空域或频域提取有效的织物特征或疵点特征,利用特征差异区分织物异常部分和正常织物纹理。空域方法包括邻域信息[4-5]、灰度共生矩阵[6]和奇异值分解[7-8]等方法;频域方法包括傅里叶变换[9]、小波变换[10-12]、Gabor变换[13-14]等方法。由于织物纹理和疵点的多样性,造成所提取特征难以适应不同种类的织物及疵点,非特征提取检测方案中,Gabor滤波是最有效的方法[13-15]。该方法无需直接提取织物纹理和疵点特征,利用一系列优化后的Gabor滤波器,直接将疵点从滤波后的图像中提取出来。然而,该方法检测结果依赖于滤波器和特定的织物纹理及疵点特征的匹配准度,且滤波器参数选择非常复杂。
近年来,基于稀疏表示的图像处理方法得到了快速的发展和较好的应用成果。基于稀疏表示的织物疵点检测方法[1],首先,通过稀疏表示原理和L1范数最小化从待测织物图像中学习出自适应字典库;然后,利用字典库求解出稀疏表示系数矩阵,重构出只包含正常织物纹理的重构图像;将重构图像与待测试图像相减,突出残差图像中的疵点区域,应用阈值分割定位出织物疵点[16]。该方法直接从待测织物图像中学习出小型字典库,且对字典库原子进行了受限优化,使该方法可重构出不同织物纹理图像,具有较高的自适应特性。然而,由于重构织物图像过程中,稀疏表示系数矩阵会出现与疵点区域对应的偏离正常范围的异常值,该算法重构正常纹理的织物图像中往往含有部分疵点,因此,疵点区域难以在残差图像中突显出来,无法检测到完整的疵点区域,经常会出现误检、漏检等情况。
本文提出基于稀疏表示系数受限优化的织物疵点检测算法。该算法从待测织物图像中学习出字典库,求解出各个图像块的稀疏表示系数矩阵,通过与正常系数矩阵比较分析,将过大和过小的异常系数元素回归正常范围,并实现对系数矩阵的受限优化;然后,利用字典库和优化后的系数矩阵对不含疵点区域的正常纹理图像进行重构,并与待测织物图像做差,得到残差图像;最后,利用最大熵阈值方法对织物图像的疵点区域和织物纹理背景进行分割[16]。
1 自适应库学习
织物图像可由一个字典库稀疏表示,获取自适应库有多种方法[1,3-4],本文采用稀疏表示和L1范数最小化方法来学习得到字典库D。利用稀疏表示方法可描述图像正常纹理和疵点特征信息;L1范数最小化方法可避免利用零范数时可能出现的难题。利用字典库D将原图像在其中线性分解,从而重构原图像目标和背景等信息。这里要求字典库仅准确表示占主要部分的正常纹理。为此,本文对待检织物图像块进行学习,用所得小型自适应字典库D对待测织物图像稀疏表示[1-3]。
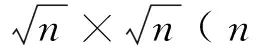

(1)

由于纱线自身具有一定弹性,正常织物纹理并没有呈现出应有的周期性,使得从标准样本图像中训练得到的字典库,不能很好地对待测织物纹理进行重构表示。然而,直接从待测图像中训练出的字典库D可准确表示织物图像的主要纹理特征,使字典库D有较强的自适应特性,因此,本文采取对待测织物图像y学习得到自适应字典库D。
2 稀疏系数矩阵优化和图像重构
2.1 稀疏系数矩阵优化
织物图像y的纹理信息yi可用学习得到的字典库D表示。考虑到重构误差对检测结果的影响,本文没有直接利用学习过程中的系数矩阵αL,而是通过对织物图像稀疏表示,用字典库D对原图像稀疏表示得到的系数矩阵α,求解α方法如式(2)所示:
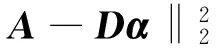
(2)
在文献[1-2]的织物疵点检测算法中,利用式(2)求得的系数矩阵α直接用于重构原织物图像,其重构方法如式(3)所示:
Ar=Dα
(3)
式中,Ar是用字典库D对A的近似表示,Ar可还原出yr即重构图像。
然而,对原图像进行稀疏表示得到的稀疏表示系数矩阵α中,相当一部分系数与正常系数差别较大,重构图像yr中包含较多疵点区域,所得到的残差图像中疵点区域突出不明显。这将导致后续的疵点检测误差较大,甚至难以检测到疵点。
周建等[2]利用织物图像纹理的周期性强和特征相关性高的特点,从待测图像中训练出仅含有4个元素的小型自适应字典库,实现了对原图像的稀疏表示;所提算法同样直接从待测图像本身训练出自适应字典库。本文选取包含了不同分辨率织物图像的图像库进行实验,发现当k=4时所重构的织物图像效果最好,因此,参数取k=4。通过对含疵点织物图像的稀疏表示系数矩阵α分析发现,α中异常元素αi,j与疵点区域存在直接关系。含疵点织物图像与正常织物图像如图1所示。图中疵点区域用黑色框标出。2副图像的稀疏表示系数矩阵元素值对比如图2所示。

图1 正常织物图像与含疵点织物图像Fig.1 Normal (a) and defect included (b)textile image

图2 优化前和优化后系数矩阵与正常织物图像稀疏表示系数 Fig.2 Sparse representation of defect included and normal textile images. (a) Before optimization; (b) After optimization
图2是所有图像块在第1个库原子的系数矩阵。j代表图像块标识号,α(i,j)代表第j图像块在第1个库原子上的系数大小,其他3个库原子与图像块的对应关系与图2类似。从图2(a)可以观察出,第159到第181图像块,即2条曲线在j∈[159,181]时,差异较为明显,因此,需要采用一种方法将含疵点系数矩阵α中的异常元素回归正常,即可重构出不含疵点的重构图像。

(4)
式中:μi和σi是系数矩阵α中第i行的均值与方差;γ是决定矩阵元素是否需要被优化的系数。通过观察发现,正常矩阵元素分布在与均值相差较小的范围内,且综合实验结果取系数γ为1.2,具体优化结果如图2(b)所示,异常系数矩阵元素已被优化至正常范围内。
2.2 图像重构
文献[1-2]中获得稀疏表示系数矩阵α后,直接将字典库D与系数矩阵α相乘得到Ar,还原Ar即为重构图像yr,但由于系数矩阵与疵点区域存在对应关系,所以重构图像yr中含有一定的疵点部分,对检测结果造成不良影响;因此,需要采用一种方法对稀疏表示系数矩阵进行优化处理,将处于异常范围的系数元素回归正常范围,使所重构织物图像中仅包含正常织物纹理。

⟺Ar=Dα*
(5)
3 算法流程
本文提出一种基于稀疏优化的织物疵点检测算法,算法由自适应库学习、原图像的系数表示、稀疏表示系数矩阵优化、图像重构及图像分割5部分组成。算法流程如图3所示。
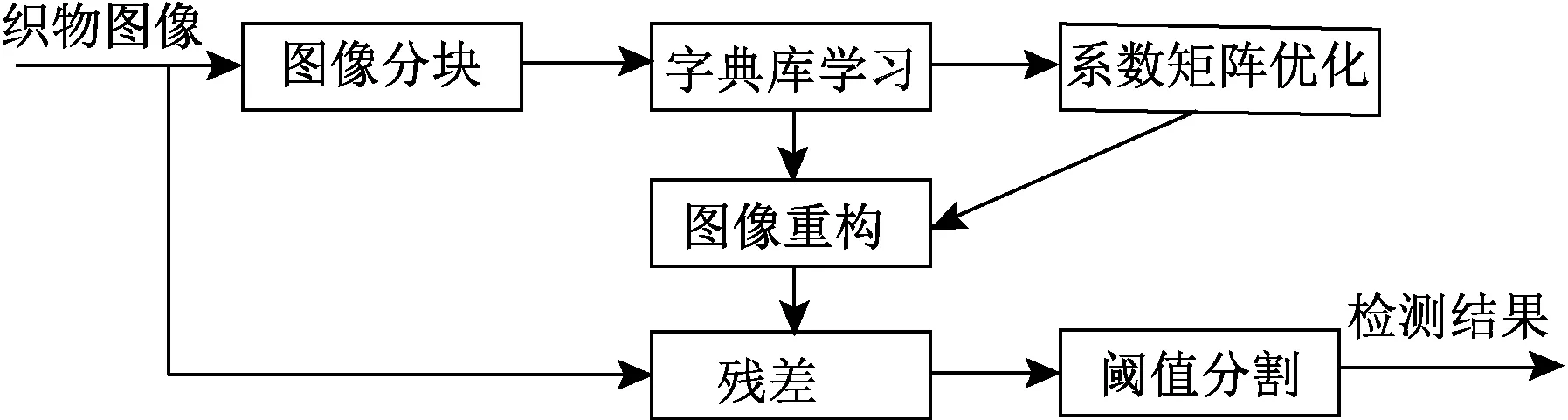
图3 算法流程图Fig.3 Flow chart of algorithm
1) 图像分块。将大小为N×N的织物图像y划分为m×m的图像yi(i=1,2,…,Nb),本文选取256像素×256像素的待测织物灰度图像。由于织物图像纹理具有较强周期性,将图像块尺寸选择稍大更为合适,否则将影响算法的运行速度。这里将图像分为16×16不重叠的图像块。
2) 自适应库训练。在式(1)中,字典库D=[d1,d2,…dk],dj∈Rm是过冗余的,而本文算法的思想是用小型字典库来表示织物图像中的正常纹理,不表示疵点部分。字典库尺寸k的选取影响着重构误差的大小,且经多次实验,库尺寸k取4较为合适。
3) 原图像稀疏表示。用所获自适应训练库D对原图像稀疏表示,获得稀疏表示系数矩阵α=[α1,α2,…αn],αi∈Rk×1。

4 实验结果与分析
本文从TILDA标准织物图像库中选出常见疵点,包括破洞、油污、褶皱等进行实验,用来验证算法的有效性。织物图像大小选为256像素×256像素。
首先,验证稀疏系数矩阵优化与否对重构图像的影响。进行自适应字典库学习之前,需要对图像进行分块,且图像块划分不易过小,可选取大小为16像素×16像素。然后,考虑到重构误差对检测结果的影响,本文字典库的尺寸取k=4,且重构误差和稀疏度平衡系数λ取1.2。原织物图像以及采用不同方法得到的重构图像如图4所示。图4示出原始待测织物图像,包括油污、褶纹、破损、裂纹、异纤等6种疵点图像。

图4 含疵点原织物图像Fig.4 Original defects obtained fabric images.(a) Oil dirt; (b) Fold; (c) Breakage; (d) Crack; (e) Foreign fiber; (f)Filling band
图5示出文献[1]方法所重构出的结果yr。该方法未对稀疏表示系数矩阵α进行受限约束,使重构结果中仍包含部分疵点区域,导致检测结果不理想。

图5 文献[1]所述方法对各种疵点的重构结果Fig.5 Reconstruction results by method of Paper [1]. (a) Oil dirt; (b) Fold; (c) Breakage; (d) Crack; (e) Foreign fiber; (f)Filling band

图6 本文方法对各种疵点的重构结果Fig.6 Reconstruction results by our method.(a) Oil dirt; (b) Fold; (c) Breakage; (d) Crack; (e) Foreign fiber; (f) Filling band

图9 文献[1]所述方法的检测结果Fig.9 Detection using by method of Paper[1].(a)Oil dirt; (b) Fold; (c) Breakage; (d) Crack; (e) Foreign fiber;(f)Filling band

图7 文献[1]所述方法的残差图Fig.7 Residual images by method of Paper [1].(a)Oil dirt; (b) Fold; (c) Breakage; (d) Crack; (e) Foreign fiber; (f)Filling band

图8 本文方法所得残差图Fig.8 Residual images using by our method. (a)Oil dirt; (b) Fold; (c) Breakage; (d) Crack; (e) Foreign fiber;(f)Filling band
图7示出系数矩阵α没有优化时的残差图像,图8示出系数矩阵优化后的残差图像。可以看出,采用文献[1]方法得到的重构图像中含疵点区域较多,可见对稀疏表示系数矩阵α进行受限约束可以使疵点区域更加突出。本文选取最大熵阈值分割方法对残差图像分割得到检测结果。为验证算法的有效性,将所提算法检测结果与已有的织物疵点检测算法进行比较,结果如图9~11所示。
图9~11检测结果中,白色部分为疵点区域,黑色部分为背景区域。图9为文献[1]的检测结果,重构系数矩阵α没有被优化,直接被用来重构原织物图像。虽然该方法可以检测到疵点,但疵点部分无法在显著图中完全凸显,导致检测效果不理想;图10为文献[16]的检测结果,其中,第1、2、5幅图像检测结果较好,但仍存在一部分噪声,第3幅图像中由于织物背景和织物疵点较复杂,检测结果较差,第4、6幅检测结果中包含较多误检疵点;图11示出本文算法的检测结果,可以看出,本文算法可有效地实现各种疵点背景与疵点区域的分离,且检测结果较前2种检测方法更好。

图10 文献[16]所述方法的检测结果Fig.10 Detection results by method of Paper[16].(a)Oil dirt; (b) Fold; (c) Breakage; (d) Crack; (e) Foreign fiber;(f)Filling band

图11 本文方法的检测结果Fig.11 Detection results by our method.(a)Oil dirt; (b) Fold; (c) Breakage; (d) Crack; (e) Foreign fiber;(f)Filling band
5 结 语
本文利用稀疏性表示方法提取织物图像的主要正常纹理特征,即学习出自适应训练库,且对原织物图像进行稀疏性重构,从而将原织物图像与重构图像做差,得到织物残差显著图,突出疵点部分;由于算法从待测织物图像中训练字典库,使得算法适应性较好。为方便与其他同类算法比较,本文采用标准织物图像库TILDA验证算法的有效性。实验结果发现,现有的稀疏性表示方法不能很好地描述织物的主要纹理特征和检测复杂背景中的疵点区域,所提算法可为所选含疵点织物图像建立较为有效的视觉显著图,凸显疵点区域;后续采用最大熵阈值分割方法实现了显著图像的有效分割和定位。本文算法为利用稀疏性表示方法在织物疵点检测方向的应用提供了新方法。
[1] ZHOU J, WANG J. Fabric defect detection using adaptive dictionaries[J]. Textile Research Journal, 2013, 83(17): 1846-1859.
[2] ZHOU J, SEMENOVICH D, SOWMYA A, et al. Dictionary learning framework for fabric defect detec-tion[J]. The Journal of The Textile Institute, 2014, 105(3): 223-234.
[3] ZHU Q, WU M, LI J, et al. Fabric defect detection via small scale over-complete basis set[J]. Textile Research Journal, 2014, 84(15): 1634-1649.
[4] 刘洲峰, 赵全军, 李春雷, 等. 基于局部统计与整体显著性的织物疵点检测算法[J]. 纺织学报, 2014, 35(11): 62-67. LIU Zhoufeng, ZHAO Quanjun, LI Chunlei, et al. Fabric defect detection algorithm using local statistic features and global saliency analysis [J] Journal of Textile Research, 2014, 35(11): 62-67.
[5] 王钢, 周建, 汪军, 等. 基于奇异值分解的机织物瑕疵检测算法[J]. 纺织学报, 2014,35(7): 61-66. WANG Gang, ZHOU Jian, ZHANG Jun, et al. Woven fabric defect detection algorithm based on singular value decomposition [J] Journal of Textile Research, 2014, 35(7): 61-66.
[6] BU H, WANG J, HUANG X. Fabric defect detection based on multiple fractal features and support vector data description[J]. Engineering Applications of Artificial Intelligence, 2009, 22(2): 224-235.
[7] CHAN C, PANG G K H. Fabric defect detection by Fourier analysis[J]. IEEE Transactions on Industry Applications, 2000,36(5):1267-1276.
[8] KIM S C, KANG T J. Texture classification and segmentation using wavelet packet frame and Gaussian mixture model[J]. Pattern Recognition, 2007, 40(4) 1207-1221.
[9] 杨晓波. 基于自适应离散小波变换的混合特征畸变织物疵点识别[J]. 纺织学报, 2013, 34(1): 133-137.
YANG Xiaobo. Fabric defect detection based on an adaptive discrete wavelet hybrid features distortion transform [J] Journal of Textile Research, 2013, 34(1): 133-137.
[10] 管声启, 高照元, 吴宁, 等. 基于视觉显著性的平纹织物疵点检测[J]. 纺织学报, 2014, 35(4): 56-61. GUAN Shengqi, GAO Zhaoyuan, WU Ning, et al. Plain fabric defect detection based on visual saliency[J]. Journal of Textile Research, 2014, 35 (4): 56-61.
[11] ARIVAZHAGAN S, GANESAN L, BAMA S.Fault segmentation in fabric images using Gabor wavelet transform[J]. Machine Vision and Applications,2006,16(6): 356-363.
[12] HOANG M C, RAJAN D. Sparse likelihood saliency detection[C]//Acoustics, Speech and Signal Processing(ICASSP),2012 IEEE International Conference. [S.l.]: IEEE,2012:897-900.
[13] JUNG C, KIM C. A unified spectral-domain approach for saliency detection and its application to automatic object segmentation[J]. IEEE Transactions Image Processing, 2012, 21(3): 1272-1283.
[14] GOFERMAN S, ZELNIK-MANOR L, TAL A. Context aware saliency detection[J]. Pattern Analysis and Machine, 2012,34(10):1915-1926.
[15] 李春雷, 张兆翔, 刘洲峰, 等. 基于纹理差异视觉显著性的织物疵点检测算法[J]. 山东大学学报 (工学版), 2014, 44(4): 1-8. LI Chunlei, ZHANG Zhaoxiang, LIU Zhoufeng, et al. A novel fabric defect detection algorithm using textural difference-based visual saliency model[J].Journal of Shandong University (Engineering Science), 2014, 44(4): 1-8.
[16] LIU Z F, WANG J G, ZHAO Q J, et al. A fabric defect detection algorithm based on improved valley emphasis method[J]. Research Journal of Applied Sciences(Engineering and Technology), 2014, 7(12): 2427-2431.
Fabric defect detection algorithm based on sparse optimization
LIU Zhoufeng, YAN Lei, LI Chunlei, DONG Yan, LI Yang
(SchoolofElectricandInformationEngineering,ZhongyuanUniversityofTechnology,Zhengzhou,Henan451191,China)
A novel fabric defect detection algorithm based on sparse optimization is proposed. Firstly, an adaptive dictionary is learned from test fabric image using L1-norm minimization method, the test fabric image is sparsely represented using the learned dictionary, and then the coefficient matrix of sparse representation is calculated. Secondly, the abnormal coefficients are removed using optimization function, then a new image is reconstructed using the optimized coefficient matrix and the dictionary. Finally, the reconstructed image is subtracted from original test image to acquire a residual image, and then the maximum entropy threshold method is used to segment the defect region. Experimental results demonstrate that the proposed algorithm has higher detection accuracy compared with the state of the art.
L1-norm; sparse representation; textile image; defect detection
10.13475/j.fzxb.20150400407
2015-04-03
2016-01-08
国家自然科学基金项目(61379113, 61202499);河南省基础与前沿技术研究计划项目(142300410042); 郑州市科技领军人才项目(131PLJRC643)
刘洲峰(1962—),男,教授,博士。研究方向为图像处理与目标识别。E-mail:lzhoufeng@hotmail.com。
TP 391.9
A
