开幅热定型机超喂控制系统模型分析
2016-07-12刘顺菁金福江周丽春
刘顺菁, 金福江, 周丽春
(华侨大学 信息科学与工程学院, 福建 厦门 361021)
开幅热定型机超喂控制系统模型分析
刘顺菁, 金福江, 周丽春
(华侨大学 信息科学与工程学院, 福建 厦门 361021)
针对现在热定型生产过程中多数依靠人工经验调节超喂量,并未建立超喂控制系统的精确模型,也未分析系统的稳定性,故常出现控制精度不高,控制系统不稳定,控制器参数整定困难的问题,通过分析超喂装置的机械结构与系统组成,得出超喂量与车速之间的关系,提出建立超喂控制系统的模型,并利用劳斯判据求出系统的稳定约束条件以及运用根轨迹方法求得系统的临界稳定增益,确保系统稳定及控制精度,实现热定型生产过程中超喂量的精确自动控制。实验结果验证了超喂控制系统模型的正确性和稳定分析方法的有效性,系统实现了对超喂量的精确定量控制。
热定型机; 超喂; 系统建模; 稳定性
热定型可提高织物尺寸与质量的热稳定性,有效消除织物上的皱痕,改善手感[1]。通过对热定型机中加热温度、车速、超喂及拉幅量等参数控制,可实现对织物的质量如面密度与幅宽的控制[2]。其中控制面密度的主要操纵变量是超喂量,超喂增加引起纤维密度增大,导致面密度增加[3]。超喂的本质是调整喂布轮进布的速度,克服织物在热定型加工中因受拉力导致布匹伸长和幅宽变窄的不稳定状态,保证纺织品定型后的成品尺寸、面密度稳定一致,达到而不超过客户要求,故超喂量的精确控制显得尤为重要,它是实现布匹面密度精确控制的基础。
对于超喂控制系统的研究,美国API自动化有限公司研究推出的YCS超喂自控系统,采用前馈控制算法,能够最大程度实现超喂的自动控制,从而保证织物的品质;国内大都采用电气设计的方法[4-5],单独对超喂电动机进行转速控制,使超喂辊的速度与传送链条速度成一定的函数关系[6],但是研究中并未建立精确的控制模型,也没有考虑生产过程中其他因素的影响;有相关研究[7]还推导了超喂电动机转速与纱线张力的数学模型,设计张力与超喂电动机间控制框图与驱动电动机的方案,仿真效果验证了控制方案的可行性。
目前染整热定型实际生产过程中大多依据工人的操作经验,采用改变热定型机入口处喂布轮线速度的方法调节超喂量。由于没有建立超喂系统的模型,导致系统控制精度不高。当车速变化或存在某些外界干扰时,原已设定好的超喂量不再适应变化后的系统,使得系统不稳定,最终导致布匹质量不合格。另外,由于超喂的控制依赖人工,生产处于半自动化状态,只有在产品质量出现明显问题时,工人才意识到超喂控制方案的错误性,再而进行调整。这不仅使控制存在严重的滞后性,也造成了资源浪费与能源损耗。针对上述问题,本文通过分析超喂与车速间的关系,建立超喂控制系统的模型,实现超喂量的自动精确控制。并运用劳斯判据与根轨迹方法求出超喂系统稳定约束条件与临界稳定增益,实现超喂控制系统参数的定量设计,保证超喂控制系统的稳定性与可行性。
1 超喂控制系统组成与构造
1.1 超喂率
织物进入的线速度即为喂布轮线速度,布夹链的线速度即为车速,二者之间的比值称为超喂率,计算公式为
(1)
式中:δ为超喂率,%;v1为车速,m/min;v2为喂布轮线速度,m/min。
1.2 超喂控制系统的装置
超喂控制系统的机械装置图如图1所示。超喂控制系统按顺序可分成2部分:一是喂布轮装置,二是热定型车床中的针铗链条装置。织物进入针铗前,先通过上下超喂辊,随即通过左右两边的探边器自动调整运行织物布边与针铗上针的距离,从而将织物夹牢送入针板处,再由2只毛刷轮将布边压入钢针根部。其中一般上超喂辊的线速度大于针铗链条的线速度。
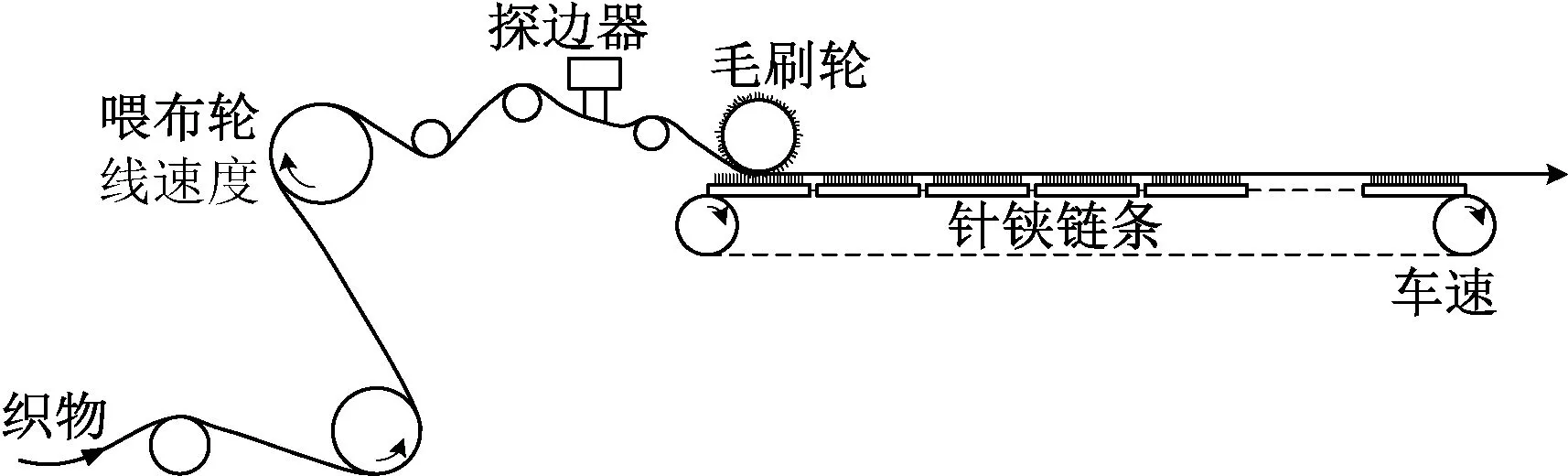
图1 超喂控制系统装置图Fig.1 Overfeed control system device
1.3 超喂控制系统的组成
依照超喂控制系统装置中的分块,可将超喂控制系统分成2部分进行控制。
喂布控制系统:该系统包括喂布轮、驱动电动机、变频器、旋转编码器和控制器5个部分。其功能是调节喂布轮转速,故该系统本质上是一个测速控制系统。
同步速度调节控制系统:该系统的结构与喂布控制系统相似,主要包括传动轮、驱动电动机、变频器、旋转编码器和控制器5个部分。系统的功能是调节定型机运行的车速。同理,该系统实际上也是一个测速控制系统。
1.4 超喂控制系统的控制
超喂量的控制本质是对喂布轮线速度的控制。对式(1)进行等式变换后发现,喂布轮线速度与车速之间存在着如式(2)的关系。
v2=(1+δ)v1
(2)
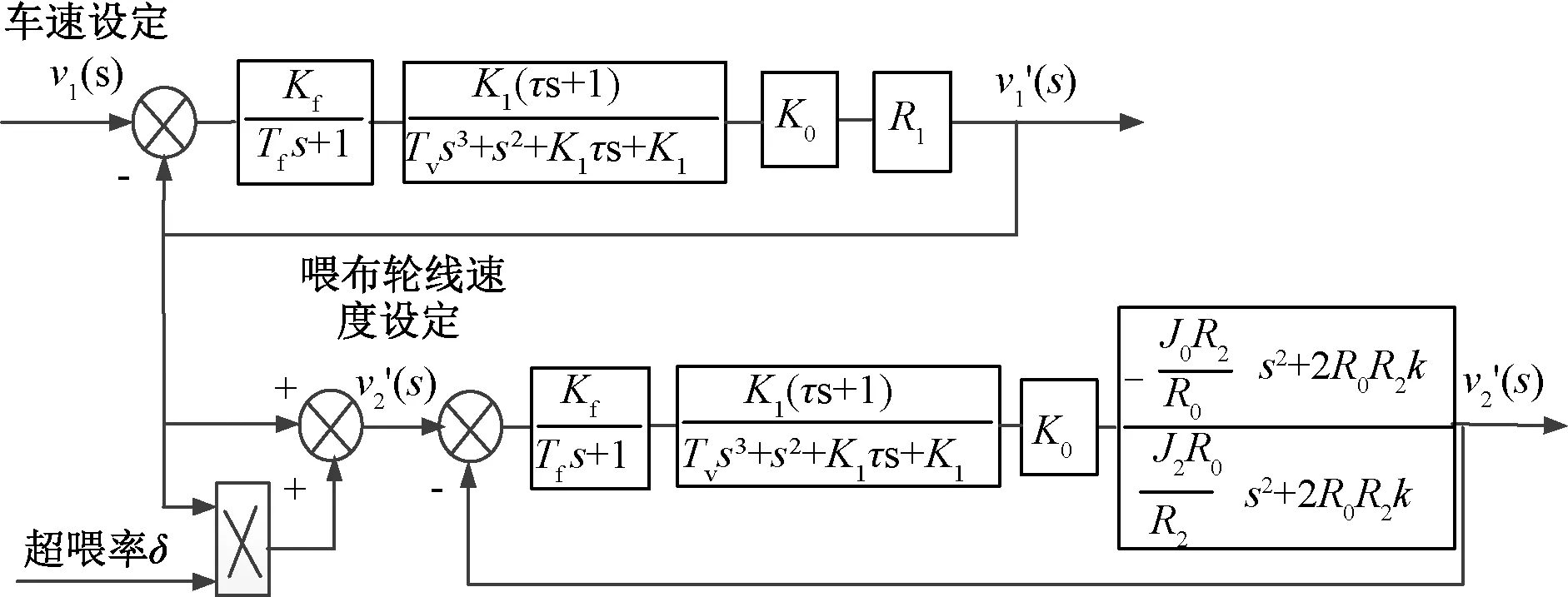
通过设定超喂率δ和车速v1可运算得出喂布轮线速度的设定值,从而实现喂布轮线速度v2的自动控制。通过此关系连接2个测速控制系统,设计超喂控制系统的整体控制框图,如图2所示。

图2 超喂控制系统的控制框图Fig.2 Overfeed system control block diagram
2 超喂控制系统模型的建立
依照超喂控制系统的控制框图,现分别对系统内的各个模块建立数学模型。
2.1 变频器异步电动机模块
变频器是三相异步电动机进行调速必不可缺的设备。通过改变频率,最终使得三相异步电动机的转子转速发生变化。当变频器频率加速度时间为零时,相当于没有给定积分器,可以对异步电动机进行矢量控制[8-9]。所谓矢量控制就是以转子磁场定向,用矢量变换的方法实现对三相异步电动机转速和磁链控制的完全解耦,达到与直流电动机一样的调速性能[10]。换言之,经过矢量变换后,可以对异步电动机的转矩电流和励磁电流分别进行类似于直流电动机的控制[11]。在基频以下的调速,励磁电流是恒定的,故类似于对直流电动机调速系统采用转速电流双闭环设计[12]。电流环按照典型1设计,为内环;转速环按照典型2设计,为外环。只对转速环进行分析可知,转速环子系统的传递函数为
(3)

转速电流双闭环调速系统中转速环的转速调节器ASR取PI比例积分调节,其传递函数表示为
(4)
式中:Kp为PI调节器的比例系数;τ为时间常数,s。
在实际生产中,可以针对具体的情况将变频器的传递函数设定为一个小的惯性环节或者一个比例环节。然后可以通过实验确定时间常数Tf,比例系数可通过Kf=50 Hz/10 V=5 Hz/V计算得到。


图3 变频器异步电动机模块动态结构图
Fig.3 Dynamic structure of inverter & asynchronous motor module
2.2 减速器模块
减速器是将电动机的回转数减到所要的回转数并得到较大转矩的机构,其关系如式(5)所示。
k=n/n′
(5)
式中:k为速比,也称传动比;n为电动机输出转数,r/min;n′为减速器输出转数,r/min。
建模时将减速器模块设计为一个比例环节。
(6)

2.3 传动轮模块
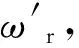
传动轮角速度与线速度的关系为
v1=R1ω1
(7)
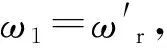
(8)
2.4 喂布轮模块
布匹通过下超喂辊传送到上超喂辊。考虑2只超喂辊间的布匹是变形体,具有一定的弹性,弹力大小为Fn。根据上、下超喂辊转速的不同,存在以下2种受力情况,其中,n0、n2分别为下、上超喂辊的转速。
如果n0>n2,布匹处于松弛状态,这易造成上下超喂辊间布匹的堆积,从而使布脱离下超喂辊,待通过上超喂辊将中间堆积的布展平后,又会重复堆布与脱辊的动作,这在生产上是不合理的,故不考虑这种状态。
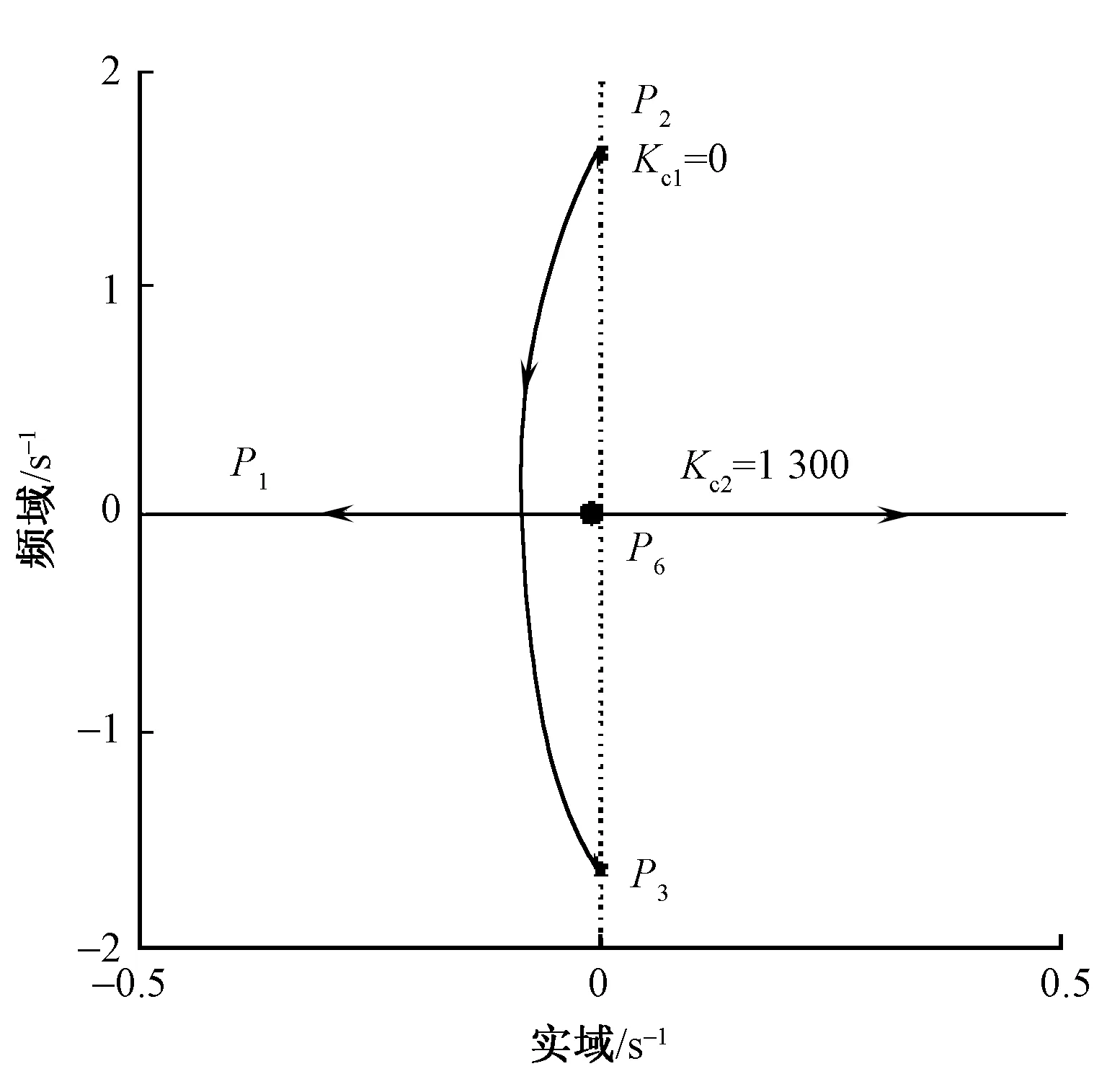
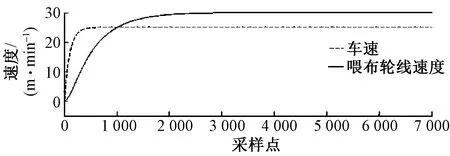
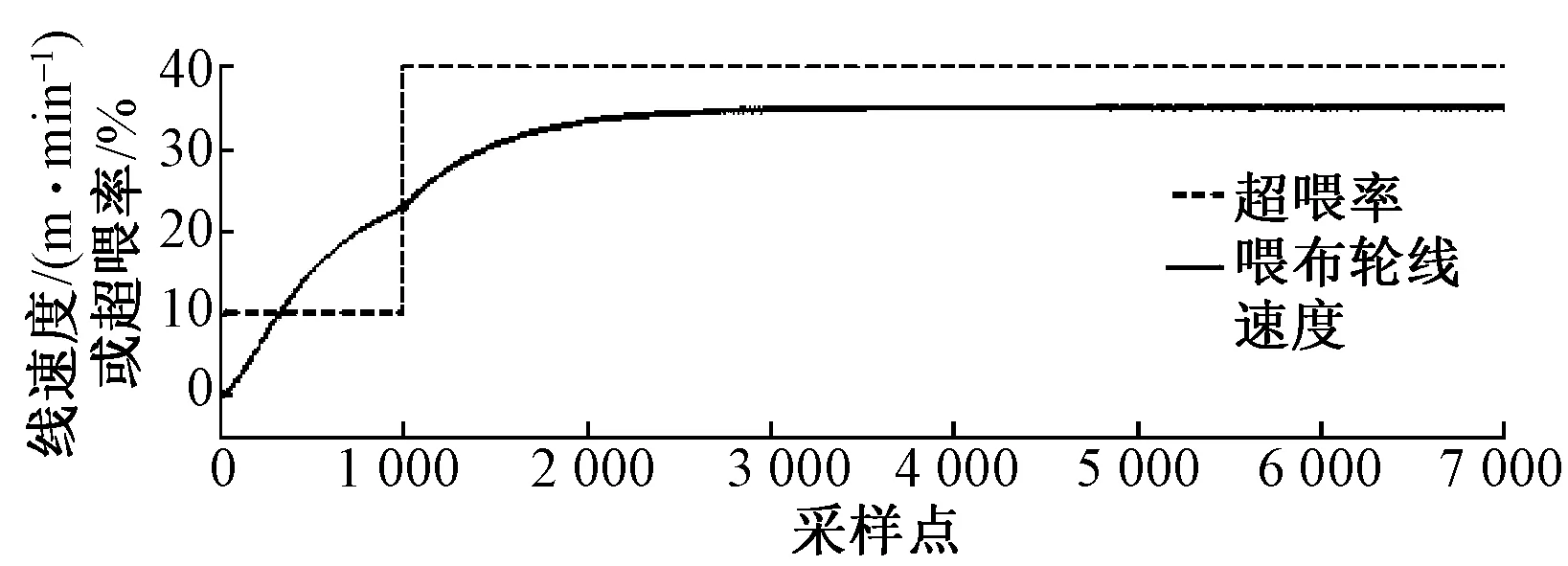
如果n0 图4 对布的受力分析 Fig.4 Force analysis for fabric 以布为对象其受力分析如图4所示。对于布,除了受到拉伸弹力Fn和自身重力FMg外,在布与上下超喂辊接触各位置处,还受到辊对布的静摩擦力△Ff,这些静摩擦力的总和设为Ff。故对于布在与上下超喂辊接触面处的受力分析可得式(9)、(10),此处设定力向上为正方向。 下超喂辊处: Ff0=Fn-FMg (9) 上超喂辊处: Ff2=Fn+FMg (10) 以超喂辊为对象受力分析如图5所示。 图5 对上下超喂辊受力分析Fig.5 Force analysis for upper and lower overfeed roller (11) (12) 除此之外,布上的拉伸弹力Fn对与其接触辊面的作用力表现为布沿其与辊面的法线方向压向辊面的正压力△Fn,方向指向辊心,且△Fn压力大小的总和为Fn,因此,由受力分析可知,辊的合外力矩只有摩擦力矩。设定力矩的正方向为垂直纸面向外的方向。 对于下超喂辊有 (13) 对于上超喂辊有 (14) 式中:J0、J2为下超喂辊与上超喂辊的转动惯量,kg·m2;α0、α2为下超喂辊与上超喂辊的角加速度,rad/s2;R0、R2为下超喂辊与上超喂辊的辊半径,m。其中角加速度为 (15) 假设布匹发生弹性形变的位移为△x,弹性系数为k,又因为在dt时间内布匹形变的变化量是由上下超喂辊的速度差决定的,故得弹力Fn的最终算式: Fn=k(v2-v0)dt (16) 将式(11)、(12)、(15)、(16)代入式(13)、(14)后两式相加,经拉氏变换整理得 (17) 2.5 系统模型 将上述各个模块整理构成超喂控制系统的整体框图,如图6所示。 图6 超喂控制系统的整体模型Fig.6 Overfeed control system′s global model 3.1 喂布轮跟随系统 假定车速与超喂率均已知,且数值恒定。现主要讨论系统中喂布轮线速度跟随系统中广义控制对象的稳定性条件。 喂布轮线速度的开环传递函数为 (18) 式中: H=XC,I=YC,M=ZC+XD, N=VC+YD,O=K1C+ZD, P=VD,K=K1D (19) X=TfTv,Y=Tf+Tv,Z=TfK1τ+1 V=(Tf+τ)K1,W=KfK1K0 (20) 3.2 劳斯稳定判据 由喂布轮线速度的开环传递函数Gv2-open(s)可得其特征多项式: ρv2(s)=Hs6+Is5+Ms4+Ns3+Os2+Ps+K (21) 为该多项式列出劳斯表,如表1所示。 表1 劳斯表Tab.1 Routh table 该跟随系统对象为稳定的充分必要条件是表1中的第1列全部为正,即有: H>0I>0S41>0S31>0 S21>0S11>0S0>0 (22) 3.3 系统的稳定条件 已知如下系统参数。 变频器参数:Kf=5 Hz/V,Tf=0.1 s。 异步电动机参数:np=2,Lm=0.081 3 H,L1=0.084 H,J=0.3 kg·m2。 减速器参数:速比k=10∶1,所以K0=0.1。 喂布轮参数:上下超喂轮半径R0=0.08 m,R2=0.1 m; 转动惯量J0=0.032 kg·m2,J2=0.075 kg·m2。弹性系数k=10 N/m。 未知参数有Kp,τ,Tv。将上述参数代入式(22)中,求得该跟随系统中控制对象稳定时Kp,τ,Tv的稳定约束条件: (23) 4.1 传递函数化简 根据系统开环传递函数的零极点分布,通过作图求得闭环极点在S平面内随回路增益变化的轨迹[13]。将喂布轮线速度的开环传递函数Gv2-open(s)中分子分母多项式化为多项式,如式(24)所示。 Gv2-open(s)= (24) 4.2 系统根轨迹 由式(23)可知,为确保系统对象在稳定范围内,可分别取τ=100 s,Tv=10 s,Kp=1,并将上述已知参数代入后分别求得W、B、D、H、I、M、N、O、P、K的数值。再利用MatLab作出系统根轨迹,如图7所示。由图可知,该系统有6个极点和3个零点。 图7 喂布轮跟随系统根轨迹Fig.7 Root locus of infeed roller following system 4.3 系统的临界稳定增益 依照上述给定参数与稳定性分析条件,运用MatLab/Simulink对系统进行仿真验证。 给定喂布轮跟随系统的输入为阶跃信号,稳态值为v2=30 m/min。系统仿真框图如图9所示。 1)若系统比例增益在稳定范围0 图8 系统根轨迹临界增益Fig.8 Critical margin in system′s root locus 图9 喂布轮跟随系统仿真框图Fig.9 Simulation diagram of infeed roller following system 图10 稳定条件内的系统仿真图Fig.10 System simulation diagram under stability condition 2)若系统的比例增益Kc>26。取Kc=30,则系统仿真结果图见图11。由图可知,如果比例增益不在临界稳定增益范围内,系统是不稳定的。 图11 稳定条件外的系统仿真图Fig.11 System simulation diagram in instability condition 在上述所求的稳定条件范围内选取1组参数,运用MatLab/Simulink对整体系统进行仿真。 1)设置车速为阶跃信号,数值v1=25 m/min,超喂率为常值输入,数值为δ=0.2。调节PID参数,车速环:kp=0.01,ti=0.2,td=0.8;喂布环:kp=0.006,ti=0.004,td=0.005,得到系统稳态时的仿真结果,如图12所示。结果表明,当超喂率不变时,喂布轮线速度v2最终能跟踪上车速v1的变化,且它的最终稳定值达到理论计算值v2=30 m/min。 图12 超喂控制系统仿真结果图(I)Fig.12 Overfeed control system simulation results (I) 2)设置车速为常值输入,数值v1=25 m/min,超喂率为阶跃信号,初始值为δ=0.1,在采样点为1 000时,数值变化为δ=0.4。调节PID参数,得到系统稳态时的仿真结果,如图13所示。结果表明,当车速不变时,喂布轮的线速度能跟踪上超喂率的变化,最终能达到稳态,并且稳态值符合理论值v2=(1+0.4)×25 m/min=35 m/min。 图13 超喂控制系统仿真结果图(II)Fig.13 Overfeed control system simulation results (II) 3)设置车速为如下的分段函数输入,超喂率为常值输入δ=0.2。 (25) 观察喂布轮线速度的跟随情况,结果如图14所示。由图可知,车速跟随系统能快速跟随复杂输入信号的变化,同时喂布轮跟随系统也能较快地跟随车速跟随系统的变化,并且达到准确的稳态理论值,因此,系统具有良好的可行性与适应性。 图14 超喂控制系统仿真结果图(III)Fig.14 Overfeed control system simulation results(III) 本文建立了超喂控制系统的模型,通过劳斯判据与根轨迹求出了超喂系统稳定的约束条件与临界增益,确保系统的稳定性。通过实验验证了系统稳定性条件的正确性及系统良好的可行性、适应性。本文提出的超喂控制系统,在生产中极大地减少了人工调节的随意性,可实现超喂量的精确控制,适应生产中时刻变化的工况,同时也减少了因调节失误造成的资源浪费。 [1] BEDELOGLU, AYSE. The influence of heat-setting process on physical properties of ribbon-type fancy yarns and fabrics produced from them [J]. Industria Textila, 2014, 65(1):3-9. [2] YANG R H. KAN C W. Effect of heat setting parameters on some properties of PLA knitted fabric [J]. Fibers and Polymers, 2013, 8(14): 1347-1353. [3] 姜岩, 张相宇, 姜丽, 等. 空气变形工艺对成纱熵变的影响[J].纺织学报,2012, 33(9): 26-29. JIANG Yan, ZHANG Xiangyu, JIANG Li, et al. Effects of air-texturing process on texturing entropy change[J]. Jouranal of Textile Research, 2012, 33(9): 26-29. [4] 李金热. 基于PLC的拉幅定型机控制系统设计[J].制造业自动化, 2010, 32(11): 134. LI Jinre. Design of control system for the tentering and setting machine based on PLC[J]. Manufacturing Automation, 2010, 32(11): 134. [5] 曾雄洪. 基于PROFIBUS-DP现场总线的拉幅定型机自动控制系统设计[D].济南:山东大学, 2012: 11. ZENG Xionghong. Design of automatic control system for stenter frame based on PROFIBUS-DP[D].Jinan:Shandong University, 2012: 11. [6] 孟宪朋. 拉幅定型自动控制系统关键点研究及人机界面设计[D].济南:山东大学, 2012: 27. MEN Xianpeng. Key points research and human machine interaction design of automatic control system for stenter frame[D]. Jinan: Shandong University, 2012: 27. [7] 陈林. 纺织超喂电动机驱动器的研制[D].杭州:浙江大学,2013: 12. CHEN Lin. The research and development of overfeeding motor driver for winding[D].Hangzhou: Zhejiang University, 2013: 12. [8] 吕华林.异步电动机矢量控制变频调速系统的研究[D].武汉:武汉理工大学, 2010: 7-18. LÜ Hualin. Research of asynehronous motor vector contfol variable frequency regulating system[D].Wuhan:Wuhan University, 2010: 7-18. [9] 吴金华.异步电动机无速度传感器矢量控制系统研究与设计[D].长沙:湖南大学, 2013: 10-14. WU Jinhua. The research and design of the asynchronous motor speed sensorless vector control system[D].Changsha: Hunan University, 2013: 10-14. [10] 张兴华.基于Simulink PSB的异步电动机变频调速系统的建模与仿真[J].系统仿真学报, 2005, 17(9): 99-103. ZHANG Xinghua. Modeling and simulation for variable-frequency drives of asynchronous motors based on simulink/PSB[J]. Journal of System Simulation, 2005, 17(9): 99-103. [11] 彭鞍虹.通用变频器异步电动机的传递函数[J].鞍山钢铁学院学报, 2000, 23(6): 447-449. PENG Anhong. Transmitting function of inverter-induction motor[J]. Journal of Anshan Institute of I.& S. Technology, 2000, 23(6): 447-449. [12] 陈伯时.电力拖动自动控制系统:运动控制系统[M].3版.北京:机械工业出版社, 2012: 88. CHEN Boshi. Electric Drive Automatic Control System: The Motion Control System[M]. 3th ed. Beijing: China Machine Press, 2012: 88. [13] 张丽敏,陈孝桢.自动控制原理[M]. 北京:科学出版社, 2014: 241. ZHANG Limin, CHEN Xiaozhen. Principle of Automatic Control[M]. Beijing: Science Press, 2014: 241. Analysis of overfeed control system model in open-width heat setting machine LIU Shunjing, JIN Fujiang, ZHOU Lichun (CollegeofInformationScienceandEngineering,HuaqiaoUniversity,Xiamen,Fujian361021,China) During the current heat setting process, the regulation of overfeed mostly relies on manual adjustment instead of setting up accurate model of overfeed control system and analyzing the stability of the system. As a result, the problems of low control accuracy, unstable control and difficult setting of parameters are frequently appeared. By analyzing the mechanical structure and components of the overfeed control system, the relationship between vehicle speed and overfeed was obtained, and the overfeed control system accurate model was established. System stable constraints and marginally stable gain were respectively obtained by Routh Stability Criterion and Root Locus method, which can stabilize the system and realize the automatic control of overfeed. Test results show that the overfeed control system model is correct and the method for stability analysis is effective. The system realizes the accurate quantitative control of the overfeed. heat setting machine; overfeed; system modeling; stability 10.13475/j.fzxb.20150502207 2015-05-13 2015-11-18 国家自然科学基金资助项目(61273069,61203040);福建省高校产学合作科技重大项目(2013H6016);中央高校基本科研业务费资助项目(JB-ZR1204) 刘顺菁(1990—),女,硕士生。研究方向为复杂系统建模与优化。金福江,通信作者,E-mail:jinfujiang@163.com。 TS 195.333 A


3 系统稳定性条件

4 系统根轨迹分析


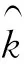
5 超喂系统稳定性验证



6 超喂控制

7 结 语
