羊绒形态结构的相关性

孙 梅， 沈淦清， 王柏华， 赵红东

(1. 河北工业大学 电气工程学院， 天津 300130； 2. 北京服装学院， 材料科学与工程学院, 北京 100080； 3. 河北工业大学 电子信息工程学院， 天津 300401)

羊绒形态结构的相关性

孙 梅1， 沈淦清2， 王柏华2， 赵红东3

(1. 河北工业大学 电气工程学院， 天津 300130； 2. 北京服装学院， 材料科学与工程学院, 北京 100080； 3. 河北工业大学 电子信息工程学院， 天津 300401)

为给羊绒选择和质量鉴定工作提供更多的理论参考，采用光学显微镜对阿里地区羊绒的直径、鳞片高度和环状鳞片占有率形态结构特征进行测试，绘制出羊绒直径-鳞片高度、羊绒直径-环状鳞片占有率以及鳞片高度-环状鳞片占有率的分布图，采用最小二乘法确定最佳拟合直线，计算了形态结构之间的相关系数，发现羊绒直径与鳞片高度有较大的正相关，环状鳞片占有率分别与羊绒直径和鳞片高度呈现较小的负相关。用阿拉善和盖县的羊绒测试结果验证了其的相关性，上面3个地区的羊绒直径与鳞片高度的相关系数平均值为0.541 4，环状鳞片占有率与羊绒直径和鳞片高度的相关系数平均值分别为-0.228 8和-0.217 0。

羊绒； 形态结构； 相关性； 分布； 拟合直线

羊绒面料轻柔保暖，美观舒适，虽然价格偏高但一直以来都受到消费者的青睐，在研究羊绒形态结构参量的同时，有必要对羊绒形态结构之间关联性进行深层次研究，已有较多的文献报道。如利用近红外光谱技术确定羊毛与羊绒光谱特性[1]，但是相比显微镜直接观察法检验成本高。孙梅等使用显微镜投影仪法测量山羊绒纤维直径，研究了山羊绒直径存在变异的现象[2]。文献[3]对羊绒形态结构特征进行了定量测试，研究了适宜统计样品数量，给出了阿拉善地区羊绒形态统计结果，确定影响羊绒直径的关键因素[4]。石先军等[5]研究了纤维鳞片纹图基因码的统计规律，表明鳞片矩形度的最优拟合为正态分布，鳞片面积等形状参数的最优拟合均为对数正态分布。沈巍等[6]应用颜色从背景图片中分离出羊绒或羊毛纤维，根据所提取纤维形状大小等特征实现羊绒检测。文献[7]利用羊绒细度、鳞片高度或密度、鳞片边界周长及鳞片面积形态参数作为比对指标，对山羊绒与细羊毛进行鉴别。有研究使用径高比、径轴参数和鳞片直角高度形态参数统计山羊绒、绵羊毛和绵羊绒的误判概率[8]。文献[9]按纤维直径划分7 类进行山羊绒鉴别。严雪萍等通过纤维细度分析仪分别对陕西榆林、白旗和阿拉善左旗3种山羊绒纤维的直径进行测量，研究3个不同地区之间的山羊绒纤维直径分布的相关性[10]。

文献[10]只对不同地区的山羊绒直径进行相关性研究，而同一地区羊绒多个形态参数间的关系仍有必要探讨。本文在已经完成的工作基础上[2]，研究多个羊绒形态参数之间的相关性，展示羊绒整体形态参数之间的关系，发现了羊绒形态参数之间的相关规律，有利于羊绒选择和质量鉴定工作的日趋完善。

1 测量方法与理论模型

本文在阿里、阿拉善和盖县3个地区采集典型的白山羊绒为实验测试样品，每个地区至少采集200根白山羊绒，在保持采集山羊绒原有形状下进行形态参量测试：在载玻片中间滴适量的浸没液，将羊绒纤维样品放入浸没液并均匀分散于溶剂中，加盖玻片，使用带ELMD彩色摄像机的日本尼康生物显微镜(ALPHAPHOT-2YS2型)观察羊绒，并通过显示屏显示的标尺测量羊绒形态结构参数，测试在室温下进行，详细测试设备及测试过程见文献[2]。

调节显微镜，可清晰观察到羊绒时测出直径。将鳞片中部调至清晰时，测量出沿纤维中心轴向鳞片间的距离为鳞片高度，统计倾斜角小于45°的环状鳞片数量，计算出环状鳞片占有率。

在测量羊绒样品中，用D、H和P分别表示羊绒直径、高度和环状鳞片的占有率样品集。

D={d1,d2,…,dN}

(1)

H={h1,h2,…,hN}

(2)

P={p1,p2,…,pN}

(3)

式中N为样品的根数，羊绒直径D、高度H和环状鳞片的占有率P中的任意2个参数在测量样品集A和B之间的相关性[11]可表示为

(4)

A,B=D or Ho r P， A≠B

(5)

ai,bi=dior hior pi， ai≠bi

(6)

(7)

(8)

(9)

(10)

为显示羊绒形态参量的相关性，采用最小二乘法对测量羊绒形态参数的数据进行拟合，即在测量参数的样品集A和B中，选择其中一个形态参量为自变量x，另一个形态参量为函数y，对应在A-B空间构成yi(xi)离散关系，令一次拟合函数为

f(x)=ξ0+ξ1x

(11)

由式(12)可确定ξ0和ξ1：

(12)

式中：min{}表示最小值；ξ0为常数项；ξ1为一次项系数。

2 结果与讨论

用测量的每根白山羊绒的直径和鳞片高度分别为横坐标和纵坐标，绘制直径与鳞片高度分布图，并根据式(11)和(12)绘制相应的拟合函数。

图1示出阿里地区200根白山羊绒的直径与鳞片高度分布图以及拟合直线。由实验结果可看出，随羊绒的直径增大，鳞片高度呈现上升趋势，通过最小二乘法公式(11)、(12)拟合出结果为：常数项ξ0=0.268 1，一次系数ξ1=0.076 8，即所测试羊绒直径H和鳞片高度D满足

H=0.268 1+0.076 8D

一次拟合系数数值较小，其原因在于羊绒直径变化范围远远大于鳞片高度。

图2示出羊绒直径与环状鳞片占有率以及拟合直线。与羊绒直径与鳞片高度分布上升变化趋势不同，随羊绒直径增加，环状鳞片数量在减少。图3示出鳞片高度与环状鳞片占有率及其拟合直线，也表明了随鳞片高度增加环状鳞片数量在减少的变化趋势。表1分别示出图1～3采用最小二乘法拟合一次曲线的常数项和一次项。

为表明羊绒直径与鳞片高度、羊绒直径与环状鳞片占有率以及鳞片高度与环状鳞片占有率的相关性，表2示出计算的各自相关系数。由计算值可知阿里地区的羊绒直径与鳞片高度为正相关，相关系数为0.627 1，羊绒直径与环状鳞片占有率为负相关，相关系数为-0.223 2，鳞片高度与环状鳞片占有率为负相关，相关系数为-0.298 1，由测试结果计算相关系数验证了图1～3的变化趋势。羊绒直径增加说明羊绒比较粗，粗羊绒上的鳞片高度增加，覆盖在较粗羊绒上面的鳞片发生倾斜较多，表现为环状鳞片数量减少，即鳞片的倾斜角小于45°的鳞片减少，但是羊绒直径与环状鳞片占有率以及鳞片高度与环状鳞片占有率相关系数的数值小于羊绒直径与鳞片高度的相关系数。

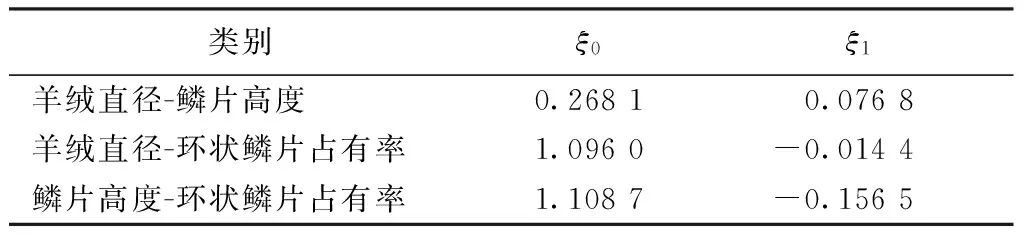
类别ξ0ξ1羊绒直径-鳞片高度0.26810.0768羊绒直径-环状鳞片占有率1.0960-0.0144鳞片高度-环状鳞片占有率1.1087-0.1565

注：ξ0和ξ1分别表示线性拟合的常数项和一次项系数。

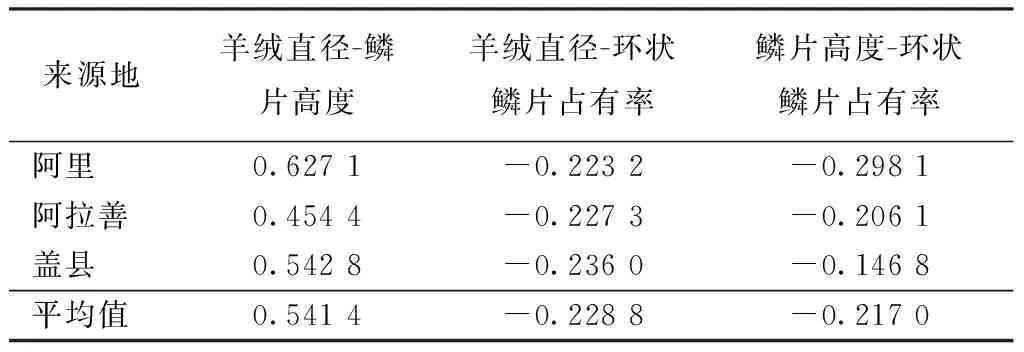
表2 阿里、阿拉善和盖县地区羊绒形态结构的相关系数及是平均值Tab.2 Correlations of cashmere morphological structure and averages in Ali, Alasan and Gaixian

为验证上述羊绒形态相关性，本文分别对阿拉善和盖县羊绒的直径、鳞片高度和环状鳞片占有率进行了测量并计算出各自羊绒的形态结构相关性，发现阿拉善地区羊绒直径与鳞片高度为正相关，相关系数为0.454 4，羊绒直径与环状鳞片占有率为负相关，相关系数为-0.227 3，鳞片高度与环状鳞片占有率为负相关，相关系数为-0.206 1；盖县地区羊绒直径与鳞片高度相关系数为0.542 8，羊绒直径与环状鳞片占有率相关系数为-0.236 0，鳞片高度与环状鳞片占有率相关系数为 -0.146 8，地区羊绒3个参数之间的相关系数及其平均值见表2所示。

3 结束语

本文对阿里、阿拉善和盖县白山羊绒的羊绒直径、鳞片高度和环状鳞片占有率形态结构特征进行了测试，研究了羊绒直径、鳞片高度和环状鳞片占有率之间的相关系数，结论如下。

1)发现羊绒直径与鳞片高度有较大的正相关，环状鳞片占有率分别与羊绒直径和鳞片高度呈现较小的负相关。

2)确定了羊绒形态参数相关性数值大小范围，羊绒直径与鳞片高度相关系数在0.5左右，羊绒直径与环状鳞片占有率以及鳞片高度与环状鳞片占有率相关系数在-0.2左右。

因此羊绒直径、鳞片高度和环状鳞片占有率之间存在一定的相关性，表明了羊绒形态参量之间的关系，对于较大正相关性的羊绒直径与鳞片高度可以检测其中一个参量从而预测另一个参量，即选择一个量作为检测标准可简化检测指标。

通过本文相关性研究可给出结论，在选择较细的羊绒生产制品时，选择的鳞片高度低、密度大以及环状鳞片较多，这种羊绒的综合形态参量性质较优异。

FZXB

[1] 吕丹, 于婵, 赵国.利用近红外光谱进行羊绒与羊毛的鉴别技术研究[J].北京服装学院学报，2010，30(2)：29-34. Lü Dan, YU Chan, ZHAO Guo.Study on identification of cashmere and wool using near infrared spectros-copy[J].Journal of Beijing Institute of Clothing Technology，2010，30(2)：29-34.

[2] 孙梅，沈淦清，王柏华，等.山羊绒形态结构统计[J].纺织学报，2003，24(1)：48-50. SUN Mei，SHEN Ganqing, WANG Baihua，et al.Statistic analysis of cashmere wool morphological structure[J].Journal of Textile Research，2003，24(1)：48-50.

[3] 贾迎宾，杨建忠，李发洲.山羊绒直径变异的研究[J].毛纺科技，2010，38(11)：48-50. JIA Yingbin，YANG Jianzhong，LI Fazhou.Study on fineness variations of cashmere fiber[J].Wool Textile Journal，2010，38(11)：48-50.

[4] 孙梅，沈淦清，王柏华，等.影响羊绒形态结构的统计规律[J]. 纺织学报，2004，25(1): 64 - 65. SUN Mei，SHEN Ganqing, WANG Baihua，et al.Statistical rules affecting pattern structure for cashmere[J].Journal of Textile Research，2004，25(1)： 64 -65.

[5] 石先军，胡新荣，蔡光明，等.羊绒鳞片纹图基因码的分布特征及相互关系[J].纺织学报，2014，35(3)：1-5. SHI Xianjun，HU Xinrong，CAI Guangming，et al.Distribution and correlation of scale pattern gene codes for cashmere[J].Journal of Textile Research，2014，35(3)：1-5.

[6] 沈巍，钱坤，尹汪宏.彩色目标提取方法检测羊绒/羊毛混纺比[J].纺织学报，2007，28(9)：31-34. SHEN Wei, QIAN Kun, YIN Wanghong.Testing of the blended ratio of cashmere wool yarns by chromatic object extraction method[J]. Journal of Textile Research，2007，28(9)：31-34.

[7] 石先军，于伟东，袁子厚.基于贝叶斯方法的山羊绒与细羊毛的鉴别[J].纺织学报，2008，29(1)：26-28，33. SHI Xianjun， YU Weidong， YUAN Zihou. An identification method for cashmere and fine wool based on Bayes model[J].Journal of Textile Research，2008，29(1)：26-28，33.

[8] 王柏华，胡志宇，葛顺顺，等.基于光镜条件下绵羊毛与山羊绒的鉴别[J].毛纺科技，2011，39(4)： 42-45. WANG Baihua，HU Zhiyu，GE Shunshun，et al.Identification of wool and cashmere based on light microscope[J].Wool Textile Journal，2011，39(4)：42-45.

[9] 杨乐芳.基于多维特征参数优化的山羊绒鉴别技术[J].东华大学学报，2009，35(4)：424-429. YANG Lefang.The identification technique for cashmere based on optimization of multi dimensional characteristic parameters[J].Journal of Donghua University，2009，35(4)：424-429.

[10] 严雪峰，陈前维，蒋丽云.山羊绒纤维直径分布的相关分析[J].毛纺科技，2014，42(4)：53-56. YAN Xuefeng，CHEN Qianwei，JIANG Liyun.Correlation analysis of cashmere fibers concerning diameter distribution[J].Wool Textile Journal，2014，42(4)：53-56.

[11] 盛骤，谢式千.概率论与数理统计及其应用[M].4版.北京：高等教育出版社2004：84-87. SHENG Zhou，XIE Shiqian.Probability Theory and Mathematical Statistics and Its Application[M]. 4th ed. Beijing: China Higher Education Press, 2004：84-87.

Study on correlation among cashmere morphological structures

SUN Mei1, SHEN Ganqing2, WANG Baihua2, ZHAO Hongdong3

(1. School of Electrical Engineering, Hebei University of Technology, Tianjin 300130, China; 2. School of Materials Science & Engineering, Beijing Institute of Fashion Technology, Beijing 100080, China; 3. School of Electronic and Information Engineering, Hebei University of Technology, Tianjin 300401, China)

The cashmere morphological structure including the cashmere diameter, the scale height and the percent of the scale ring are measured with an optics microscope for the cashmere in Ali area. The distributions for the cashmere diameter with the scale height, the cashmere diameter with the percent of scale ring and the cashmere scale height with the percent of scale ring are showed, respectively. The proper linear fittings are determined by the least squares method and the correlation coefficients are also computed among cashmere morphological structures. It shows that there is a larger positive correlation between the cashmere diameter and the scale height while the correlations between the percent of scale ring with the cashmere diameter and the scale height are smaller negative respectively. The similar correlations among cashmere morphological structures are also found in the cashmere from Alashan and Gaixian areas, respectively. The average correlation coefficient between the cashmere diameter and the scale height is 0.541 4, the average correlation coefficients between the percent of scale ring and the cashmere diameter and the scale height are -0.228 8 and -0.217 0, respectively, from above three areas.

cashmere; morphological structure; correlation; distribution; linear fitting

10.13475/j.fzxb.20150400104

2015-04-02

2016-03-07

孙梅(1969—)，女，副教授，博士。主要研究方向为信息处理。E-mail：msun@hebut.edu.cn。

TS 102.3

A