海口荣山河四线并联斜交桥桥墩河段水动力分析
2016-07-09武永新汪星
武永新 汪星

摘要:为研究海口市荣山河四线并联斜交桥桥墩河段水动力特性及不同水位下的桥墩-桥梁体系整体的自振特性,应用FLUENT及ANSYS软件,基于分离涡方法(DES法),建立了四线斜交桥河段的河槽水流三维模型,模拟了不同流速和不同斜交角度下的流场分布及流固耦合作用下的桥墩-桥梁体系自振特性。结果表明:荣山河四线并联斜交桥的过流能力可达到400 m3/s,桥下最大壅高为0.69 m,桥下留有一定安全距离;考虑流固耦合作用下的斜交桥墩-桥梁体系满水情况下的自振频率为7.66 Hz,不会与通过列车发生共振危险。
关键词:四线并联斜交桥;数值模拟;分离涡法;壅高;绕流;自振特性;共振
中图分类号:TV87 文献标志码:A 文章编号:1672-1683(2016)04-0135-07
Abstract:For the study of hydrodynamic characteristics of the bridge pier of the four-line parallel skew bridge of Rongshan River in Haikou City and the overall self vibration characteristics of the pier and bridge system under different water levels,FLUENT and ANSYS software were used,based on the DES method,the three-dimensional flow model was established for the four-line skew bridge river channel,the flow field distribution under different flow rate and different oblique angle as well as the self-vibration characteristics of the pier-bridge system under fluid solid coupling was simulated.The results showed that the maximum flow capacity of the four-line parallel skew bridge could reach 400 m3/s,and the bridge had a certain safe distance, with a maximum backwater height of 0.69 m.The natural frequency of the pier-bridge system under the condition of fluid solid coupling was 7.66 Hz,without the risk of resonance with the passing trains.
Key words:four-line parallel skew bridge;numerical simulation;DES method;backwater height;flow;vibration characteristics;resonance
1 工程概况
海口市荣山河发源于海口市石山镇的马鞍岭,流经海口市的长流镇、荣山乡和澄迈县的老城镇,于澄迈县的东水港入海,流域面积86.8 km2(不包括长丰沟流域15.48 km2),河长26.47 km,河床平均坡降为2.1‰。荣山河流域上游为丘陵区,中游为开阔河谷地貌,下游为宽水面出海河湾及滩涂带,其下游段干流是新区泄洪、排涝大动脉[1]。荣山河下游干流上连续的四座斜交铁路桥,桥址处河段相对顺直,桥墩相对位置见图2。四座铁路桥卡住了这条排涝通道,桥面与河底距离较低,且桥下过流能力未知。另外,四座斜交铁路桥是交通运输要道,桥下过流量的预测及桥墩段的水流流场分析以及桥墩-桥梁体系在流固耦合作用下的自振特性分析对桥梁安全和交通运输安全都有着非常重要的作用。
2 数学模型
2.1 控制方程
2.2 方程求解方法
分离涡方法(DES) [2]是一种利用单一湍流模式的三维非定常数值求解方法,结合了大涡模拟(LES) 和雷诺平均法(RANS) 两种方法的优点,这种方法在网格密集的地方相当于LES 中的亚格子尺度应力模式,在其余地方相当于RANS 模式。引入湍动粘度或涡粘系数参数,不直接求解雷诺应力项,用涡黏系数的函数来表示雷诺应力,整个模型计算的关键点是如何确定涡黏系数的表达式。
3 计算结果分析
3.1 计算方案
(1)流速对桥墩段水流的影响。根据荣山河斜交铁路桥河段的实际规模并经过一定简化,建立一个长300 m,宽27 m,高5 m的三维水槽,模型简化前后河道横断面图见图1。桥轴线与河道横向斜交角α为65°,河道粗糙度取0.5,圆柱桥墩直径取2.0 m,四座平行的斜交桥共12个桥墩。模型水流入口条件变化5种,分别取流速为3.7 m/s,2.8 m/s,1.85 m/s,1.0 [JP4]m/s,0.52 m/s,对应的流量分别为400 m3/s,300 m3/s,200 m3/s,108 m3/s,50 m3/s,初始水位均取4 m水深。
(2)斜交角度对桥墩段水流的影响。[HJ2.2mm]建立一个长300 m,宽27 m,高5 m的三维水槽模型,河道粗糙度取0.5,圆柱桥墩直径取2.0 m,四座平行的斜交桥共12个桥墩。四座桥轴线与河道横向斜交角α取65°,50°,35°,20°,0°(其中α=0°为正交)五种布置方案,河道进口流速取3.7 m/s,初始水位均取4 m水深。桥位布置图及桥的编号见图2。
(3)水位对斜交桥墩-桥梁体系自振特性的影响。取四线并联斜交桥中的一座桥位研究对象,取斜交角度α为65°,水位取无水工况到满水工况之间,分别为0 m,0.625 m,1.25 m,1.875 m,2.5 m,3.125 m,3.75 m,4.375 m,5.0 m。
3.2 模型设置
模型网格划分采用自适应模式,模型三维网格及桥墩局部网格加密见图3,湍流求解方法选择分离涡方法(DES法),求解器选择非耦合隐式求解,设定初始操作压力为一个标准大气压101 325 Pa,初始操作压力的参考位置坐标点选择(0,6,0 ),压力速度耦合选用SIMPLE形式,密度,速度,能量都选取二阶迎风格式,压力选为标准格式,设定收敛残差,连续方程收敛残差相对值为0.0001,x,y,z方向速度收敛残差相对值为0.000 1,能量方程收敛残差相对值为0.000 1,时间步长选择0.02 s。边界条件设定如下。
进口边界条件:进口边界采用压力进口,设定进口初始水位为4 m,水流进口流速分别为3.7 m/s,2.8 m/s,1.85 m/s,1.0 m/s,0.52 m/s。
出口边界条件:出口边界采用压力出口,设定初始水位为4 m。
固壁边界条件:设定模型中固体壁面为无滑移边界条件,其中粗糙系数均采用0.025。
3.3 不同流速下桥墩段水动力特性计算结果分析
3.3.1 桥墩段壅水分析
河槽中布置了四座斜交桥,每座桥在河槽中分别布置3个桥墩,桥墩总数12个。根据斜交桥的水流特点及尾流扩散理论,上游桥墩尾流对下游水流有干扰,下游桥墩的壅水对上游水流有影响[3-7]。以每座桥各个桥墩的最大壅高代表该座桥的壅水高度。图4是12个桥墩及四座桥在不同流速下的壅水高度。由图4可知,壅水高度有如下规律:第一座桥的壅水最高,这是由于第一座斜交桥的壅水高度只受流速的影响,受后三座桥的影响较小。距离第一座桥15 m的第二座桥下的壅水相对减小,但仍有较大的壅水高度,这是由于该座桥受第一座桥截流作用的影响,壅高减小。第三座斜交桥的桥墩壅水最小,受上两座桥截流影响大,此时壅水高度迅速减小。第四座桥的壅水高度小于第一座桥的壅水高度,说明距离上一座桥35 m时,壅水仍然受到上游桥墩影响。
根据图4(a)和4(b)显示的结果可知,流速为0.52 m/s和1.0 m/s时,12个桥墩壅水高度很小,且每个桥墩壅水高度大致相同,说明小流速的情况下水流可以顺利通过并联的四座斜交桥且不引起明显的桥墩壅水。流速大于1.0 m/s后,各桥墩壅水逐渐明显,但第一座桥壅高变化程度最大,然而各流速对第二座桥影响不明显,壅水高度始终很小。当流速为3.7 m/s时,壅水高度最高达到0.69 m,能顺利通过四座斜交桥,即桥下过流量可达到400 m3/s。但由于壅高达到0.69 m,对堤岸的防洪产生较大影响。各座桥在不同流速下的壅水高度计算成果见表1。
3.3.2 桥墩段绕流分析
对于河道中的四线斜交铁路桥而言,由于河道中桥墩数量较多,墩后的尾流呈现出不规则的涡通道。根据图5和图6可知,升阻力系数有如下规律:在五个不同的流速条件下,顺水流方向的第一座斜交桥下的三个桥墩的阻力系数最大,符合单圆柱绕流的规律。而后面三座桥下的九个桥墩的阻力系数急剧下降,甚至呈现负值,这是因为后面三座桥处在第一座桥的三个桥墩的尾流中,上一座桥的桥墩分离出的涡旋对后面的桥墩产生了向前的推力,使得阻力减小。图5(b)显示,随着流速的增大,后三座桥各桥墩的阻力系数变化很平缓但呈现出增大的趋势,这是由于流速增大后,前一座桥产生的涡旋对后面三座桥的向前的推力变大。从 图6可以看出,各个桥墩绕流的升力系数趋近于0,变化范围在10-4量级以内,可忽略不计。
3.4 不同斜交角度下桥墩段的水动力特性分析
3.4.1 桥墩段壅水高度分析
图7是12个桥墩在不同斜交角度下的壅水高度,可以得出以下规律:在各个不同的斜交角度的条件下,壅水最高的仍然是第一座桥下的三个桥墩,壅水最小的是第三座桥。图7(b)显示,随着斜交角度的增大,桥下壅水表现出平稳变化,随后减小再增大的趋势。只有第三座桥不符合这个趋势,这是由于第三座桥离第二座桥较近,水流紊乱。斜交角度为50°时,第一座桥和第四座桥的桥下壅水高度最小,产生这种现象的原因,可以从桥下水流流向偏转角度对桥墩间的过流能力影响来解释。随着斜交角度的不断增大,桥下水流的流向也不断发生变化。李付军[8]通过理论分析得到“随着斜交角度的增大,水流流向偏转角度先增大后减小,且在α介于40°~60°间取得最大值”,由于水流偏转角的存在,有效的增大了桥下过流能力,使得桥前壅水降低,且流向偏转角度越大,过流能力就越强,壅水就越小。各座桥在不同流速下的壅水高度计算成果见表2。
3.4.2 桥墩段绕流分析
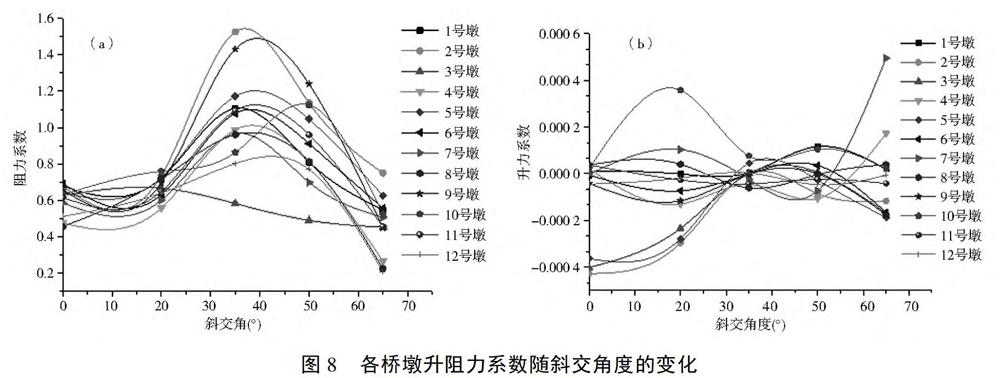
图8是不同斜交角度条件下的各桥墩的升阻力系数曲线,由图可知,斜交角度变化时,升阻力系数的变化关系比较混乱,但仍然可以确定斜交角度为35°~50°时,各桥墩的阻力系数达到最大值,此时升力系数变化较小。
3.5 流向偏转角对斜交桥前壅水影响分析
本节采用的工况为来流流速为3.7 m/s,为便于比较分析流向偏转角的变化规律,取同一座斜交桥下相邻两墩连线中点处的流向偏转角度代表两桥墩连线上各点处流向偏转角度的平均值[9-10]。
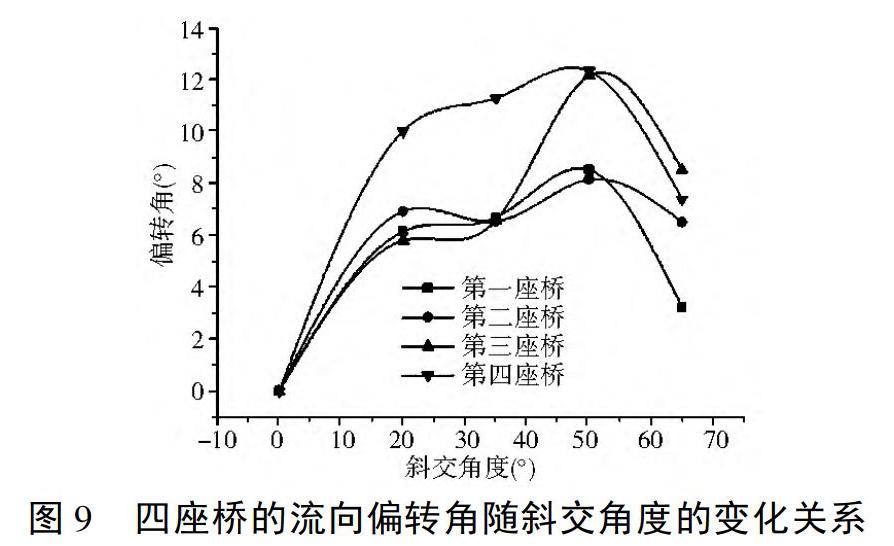
图9是四座桥的流向偏转角随斜交角度的变化关系,由下述图可知,随着斜交角度的增大,水流的流向偏转角不是一味的增大或减小,而是先增大后减小的趋势,当斜交角度为50°左右时,水流的流向偏转角达到最大值,桥下有效过流能力达到最大,此时的桥下壅水值最小与文献[11]相符。
3.6 水位对桥墩-桥梁体系自振特性的影响
为进一步研究基于流固耦合作用时水体对桥墩-桥梁体系的自振特性的影响,采用水体附加质量法,将水对结构的影响通过附加质量的形式作用于桥墩节点上[12-16]。取四线并联铁路桥中斜交角度为65°的其中一座为研究对象,桥梁简化为简支梁,梁端与桥墩之间为无伸缩缝的整体式结构[17]。模型中,桥墩及主梁材料的弹性模量取3.0 ×1010 N/m2,密度均为2 430 kg/m3,泊松比为0.28。流体的流场尺寸范围按200 m×27 m设置,流体单元采用F1uid 30单元,设置参数为:密度1 000 kg/m3,声速为1 430 m/s。[HJ2.05mm]流体与桥墩面通过设置FSI耦合标签进行传递。
通过水位改变,使得水位与墩高之比h/H值分别为0,0.125,0.25,0.375,0.5,0.625,0.75,0.875,1九种工况,计算结果见表3,可得出以下结论:体系的前两阶自振频率随着h/H增大而减小,与谭上俞[18]、刘永吉[19]计算结果一致。图10显示,h/H超过0.5后,前两阶频率降低幅度增大。文献[20]指出“荷载以速度v通过跨长L的时间等于桥梁第n阶自振周期的一半或其n倍时,就会发生共振,桥梁的位移会出现峰值。”满水工况下的一阶自振频率为7.66 Hz,桥长65 m时,发生共振的列车临界车速为995.8 m/s,远大于列车的正常运行速度,因此不会发生共振危险。
4 结论
(1)通过对海口市荣山河四线并联斜交铁路桥下的水流研究发现,过流量小于400 m3/s时,最大壅高为0.69 m,水流能顺利通过四座桥,且留有一定安全距离,但对堤岸防洪产生较大影响,需对防洪建设加强巩固。
(2) 随着斜交角度的增大,流向偏转角先增大后较小,当斜交角度为50°左右时,水流的流向偏转角达到最大值,桥下有效过流能力达到最大,此时的桥下壅水值最小,因此建议斜交桥的斜交角度取50°左右最为合适。
(3)桥墩-桥梁作为一个整体,其自振频率与水位有关,水位升高,自振频率减小,当水位超过墩高50%后,自振频率减小幅度增大。满水工况下自振频率为7.66 Hz,不会与通过列车发生共振。
(4)桥梁工程中,若修建高墩桥,自振频率变化会更大,则不可忽视流固耦合中水位对桥墩-桥梁体系的自振影响,以免产生共振毁桥的危险。
参考文献(References):
[1] 黄河勘测规划设计有限公司.西海岸新区、长秀区水系改造简介[B].2014.(The Yellow River Surveying and Planning Design.West Coast District,Changxiu District water system transformation[B].2014.(in Chinese))
[2] 王福军.计算流体动力学分析[M].北京:清华大学出版社,2004.(WANG Fu-jun.Computational fluid dynamics analysis [M].Beijing:Tsinghua University Press,2004:113-142.(in Chinese))
[3] 季日臣,何文社.斜交桥壅水试验研究与理论探讨[J].水科学进展,2007,18(4):504-508.(JI Ri-chen,HE Wen-she.Experimental and theoretical study of skew bridge backwater [J].Advances in Water Science,2007,18 (4):504-508.(in Chinese))
[4] 季日臣,刘有录,宁贵霞.多线大角度斜交桥渡模型试验研究与工程实践[J].城市道桥与防洪,2005(4):106-108.(JI Ri-chen,LIU You-lu,NING Gui-xia.Multi line big angle skew bridge crossing desert type of experimental research and engineering practice [J].Urban Roads,Bridges & Flood Control,2005(4):106-108.(in Chinese))
[5] 孙东坡,杨苏汀.公路斜交桥壅水特性[J].水利水运工程学报,2007(1):41-46.(SUN Dong-po,YANG Su-ting.Backwater characteristics of speedway skew bridges [J].Hydro-Science and Engineering,2007(1):41-46.(in Chinese))
[6] 吴飞.桥墩组中轴线与水流方向夹角对河流流场影响的数值模拟研究[J].水资源与水工程学报2009,20(2):75-78.(WU Fei.Numerical simulation research on the affection of the bigger angle between the middle-line of the piers group and the river flow [J].Journal of Water Resources & Water Engineering.2009,20 (2):75-78.(in Chinese))
[7] 杨帆.河弯处斜交桥下水流流场研究[D].成都:西南交通大学,2010.(YANG Fan.Study on flow of water under the oblique bridge[D].Chengdu:Southwest JiaoTong University,2010.(in Chinese))
[8] 李付军,张佰站,林桂宾.斜交桥下水流流向偏转角度的理论分析[J].水科学展,2005,16(5):634-637.(LI Fu-jun,ZHANG Bai-zhan,LIN Gui-bin.Theoretical analysis of the deflection degree of the flow direction under bevel bridge [J].Advances in Water Science,2005,16 (5):634-637.(in Chinese))
[9] 华维娜.山区河道圆柱桥墩的阻水特性研究[D].陕西:西北农林科技大学,2011.34-38.(HUA Wei-na.Study on water blocking performance of cylindrical bridge piers in mountain rivers [D].Shanxi:Northwest Agriculture and Forestry University,2011.34-38.(in Chinese))
[10] 王仁宽.山区斜交桥渡雍水和孔径计算[J].铁道学报,1984,1(6):84-95.(WANG Ren-kuan.Calculation of back water and span lengths of skew crossing bridges in mountainous areas[J].Journal of the China Railway,1984,1 (6):84-95.(in Chinese))
[11] 刘哲,陈春光.斜交桥下水流流向偏转角度的数值模拟[J].四川建筑,2010,30(3):126-127.(LIU Zhe,CHEN Chun-guang.Numerical simulation of the flow direction deflection angle of the inclined cross bridge [J].Sichuan Building,2010,30 (3):126-127.(in Chinese))
[12] 周刚贵.深水高墩桥梁高速列车作用下桥梁动力学分析[D].武汉:武汉理工大学,2012.( ZHOU Gang-gui.Bridge dynamics analysis of high speed railway bridge with high pier bridge [D].Wuhan:Wuhan University of Technology,2012.(in Chinese))
[13] 杨吉新,张可.基于ANSYS的流固耦合动力分析方法[J].航海工程,2008,37(6):86-89.(YANG Ji-xin,ZHANG Ke.Dynamic analysis method for fluid-structure interaction based on ANSYS [J].Ship & Ocean Engineering.2008,37 (6):86-89.(in Chinese))
[14] 苏波,钱若军.流固耦合方程的建立及耦合数据传递[C].第八届全国现代结构工程学术研讨会,2008:624-629.(SU Bo,QIAN Ruo-jun.Fluid solid coupling equation is established and the coupling data transmission [C].The Eighth National Modern Structural Engineering Conference,2008:624-629.(in Chinese))
[15] 苏波.流固耦合界面信息传递理论和方法研究进展[J].空间结构,2010,16 (1) :3-10.SU Bo.Advances in research on theory and method of data exchange on coupling interface for FSI analysis [J].Spatial structures,2010,16 (1):3-10.(in Chinese))
[16] 娄涛.基于ANSYS的流固耦合问题数值模拟[D].兰州:兰州大学,2008.(LOU Tao.Numerical simulation of fluid solid coupling problem based on ANSYS [D].Lanzhou:Lanzhou University,2008.(in Chinese))
[17] 张瑜,刘菲.特大型桥的自振特性分析[J].工程技术与产业经济,2013(1):1-3.(ZHANG Yu,LIU Fei.Analysis of the natural vibration characteristics of large bridge [J].Engineering Technology and Industrial Economy,2013(1):1-3.(in Chinese))
[18] 谭上俞.桥墩-流水耦合效应下水位变化对桥梁动力影响分析[D].重庆:重庆交通大学,2013:27-37.(TAN Shang-yu.Analysis on dynamic effects of the water level change to the bridge under the fluid-pier interaction [D].Chongqing:Chongqing Jiaotong University,2013:27-37.(in Chinese))
[19] 刘永吉.考虑流固耦合效应的水中桥墩动力响应分析[D].重庆:重庆交通大学,2012:38-40.(LIU Yong-ji.The analysis of dynamic response for bridge piers in water considering fluid-solid coupling effect [D].Chongqing:Chongqing Jiaotong University,2012:38-40.(in Chinese))
[20] 王少钦.风及列车荷载作用下大跨度桥梁振动响应研究[D].北京:北京交通大学,2012:41-43.(WANG Shao-qin.Dynamic analysis of long-span bridge subjected to cross wind and train [D].Beijing:Beijing Jiaotong University,2012:41-43.(in Chinese))
