水库多目标调度方案优选决策方法

李昱 王海霞 周惠成 张弛 张小丽

摘要：针对水库多目标调度模型生成的众多Pareto可行解，决策者往往面临方案优选决策困难的问题。提出利用可视化展示工具，结合边际效益分析及模糊优选方法，对可行方案进行逐步决策的优选决策方法。结果表明，利用不同的分析工具与决策方法，使众多可行方案得到形象可视化展示的同时，能够融入决策者的主观偏好等信息，得到具有不同决策需求的满意方案。通过不同决策方法的层层决策，逐渐减少备选方案的数量，降低了多目标决策问题的复杂性，为决策者的方案优选提供一定的参考。

关键词：多目标调度；优选决策；Pareto解；可视化工具；AeroVis；边际效益；模糊优选

中图分类号： 文献标志码：A 文章编号：1672-1683（2016）04-0048-06

Abstract：Decision makers usually face decision-making difficulties on Pareto feasible solutions generated by reservoir multi-objective operation model.To solve this problem，visualization tool together with marginal benefit analysis and fuzzy optimization method were proposed for gradual optimization of feasible solution set.The results showed that，by using different analysis tools and decision methods，feasible solutions received visual representation meanwhile some of the decision preference information was integrated to obtain the satisfactory solutions for different decision-making demands.By using different decision methods，the number of alternative solutions was reduced gradually to make the problem less complex.This paper can provide some references for multi-objective solution selection problem for decision makers.

Key words：multi-objective operation；optimal decision making；Pareto solutions；Visualization tool；AeroVis；marginal benefit；fuzzy optimization

1 研究背景

多目标调度方案的优选决策，是水库多目标调度研究的重要组成部分，对于水库实际调度效益的发挥具有重要作用。在采用多目标优化算法对水库多目标调度模型求解后，需要决策者综合一些主观及客观信息，利用一定的评价方法或筛选工具，对具有竞争关系的多目标备选方案集进行优选决策，选出符合工程实际需求的满意方案。

对于多目标决策问题，国外很早就进行了相关方面的研究。1896年，帕雷托（V.Pareto）从经济学角度提出了向量优化的概念，把本质上不可比较的多目标问题转化成单目标问题进行求解，是多目标决策研究的最早成果；1944年，冯.诺伊曼（Neumann J.V）和摩根斯坦（Morgenstern O）从对策论角度提出了彼此矛盾情况下的多准则决策问题[1]，是近代意义上多目标决策的开始；1971年，Roy等提出了ELECTRE多目标决策方法[2]，通过决策者对方案集中各方案的级别关系检验，逐步淘汰级别较低的方案，从而得到满意方案；1973年，Srinivasan等提出多维偏好线性规划决策法（LINMAP法）[3]，通过与理想解的比较，求解最优方案。随后，层次分析法[4]、部分信息法[5]、模糊决策法[6]等多目标决策方法相继产生。

国内对于多目标决策的研究起步较晚，但是也已取得了大量的研究成果。陈守煜等[7]提出了系统层次分析模糊优选模型，并将其运用到大系统多层次多方案的综合评价中，提出了两种权重计算方法；王本德等[8]研究了梯级水库群的多目标洪水调度问题，结合模糊集理论以及传统的优化技术方法，引入权重折中系数，提出了一种能统一兼顾客观决策和主观决策的水库群防洪调度模糊循环迭代模型；杨俊杰等[9]通过对决策方案集的对立同一描述，得到了不确定情况下的联系数矩阵，并利用联系数中的差异度信息，对决策优选结果进行稳定性分析；周晓光等[10]通过计算Vague集下各指标的正、负理想加权距离，计算指标函数的评价值；李英海等[11]针对现有Vague集决策方法的局限性，提出了基于改进熵权和Vague集理论构建的多目标优选决策方法，等等。

大伙房水库输水应急入连工程实施后，碧流河水库的调度中包含引水、工业与生活、农业、生态环境等多个目标。由于各个目标之间存在竞争关系，因此不可能得到一个令所有目标均为满意的全局最优解，而只能得到一组Pareto最优解集。虽然目前对于多目标决策的方法较多，然而大部分决策方法均是以定量分析为基础，缺少对中间决策过程的形象展示。因此，根据决策需求，借助一定的展示工具，并结合相应的评价方法或筛选工具，在逐步降低多目标优选决策问题复杂性的同时，将决策过程形象的展示出来，为决策者提供可视化的、定性与定量相结合的优选决策过程，具有重要意义。

2 方法介绍

2.1 可视化技术

计算机软、硬件技术水平的不断提升，使人们对数据的处理速度大大加快，图形学及图像处理等技术也随之被用于数据的后处理过程当中，以发掘数据内部不易被观察和理解的信息。通过将数据结果以图形形式形象、直观地展示出来，为人们分析、理解数据以及找出规律提供了强有力的手段[12]。

在多目标优化问题中，随着目标函数的增加，人们对解的分析和理解更加困难，增加了决策者的决策难度。可视化技术通过对最优前沿解的可视化展现与分析，为决策者决策和算法优化提供了很好的辅助作用，因此成为目前多目标优化方案优选问题研究的热点之一[13-15]。

对于高维多目标优化问题的可视化技术实现，关键在于对数据的分析以及对分析结果的可视化工具显示两个方面。目标数据的可视化显示中，显示工具的构成元素，主要包括以下方面。

（1）空间三维图形。对于不同的目标维度，以不同图形元素的组合和变换来表示。通过图形的密度和颜色分布情况，可以给出决策者优化目标分布情况以及目标之间相关性等信息；

（2）颜色图。主要包括彩色图和灰度图两种。彩色图中不同的颜色代表不同属性维中数据的大小，而灰度图中则利用颜色的深浅来表示数据量的属性值大小，其中，颜色的深浅分布代表目标整体的分布情况。

（3）亮度。用不同的亮度来标识特定的区域，辅助人眼对特殊区域的观察。

总之，可视化技术极大地提高了数据计算的速度和质量，成为很多领域必不可少的数据后处理部分。它使计算中产生的大量高维数据，通过可视化技术变成图形，激发人们的形象思维能力，增强对数据理解的深度与广度。目前，可视化技术已被广泛应用于数学、生物、医学、地质、气象、建筑等各种领域，为决策者决策提供依据。

2.2 边际效益原理

边际效用是指在一定时间内消费者增加一个单位商品或服务所带来的新增效用，也就是总效用的增量[16]。在水库的多目标调度方案决策问题中，边际效用即是边际增加1单位对某个特定用水户的供水，所导致的其调度目标的提升值[17]。在水资源总量有限的情况下，对某个用水户供水量的增加，必然导致对其它用水户供水量的减少。因此，边际效用同时表现为，通过对某个调度目标值的降低，而达到的对其它目标的改善程度。

2.3 模糊优选决策

模糊决策是一种将决策信息进行模糊化处理的决策方法，由于备选方案集的数值难免存在不精确或者决策专家主观权重难以量化描述等问题，通常采取将这些数值进行模糊化处理，从而提高决策过程的可靠性[18-19]。对于水库多目标调度模型生成的Pareto解集，模糊优选模型[20]可在综合考虑供水、社会、经济、生态环境等各方面因素影响的情况下，把多个不同量纲的评价指标转化为相对评价指标，并将各个目标的相对优属度与目标权重有效地结合，获得经过模糊量化的定量结果，为多目标优化方案的综合评价提供一种有效的决策方法。

3 水库多目标调度方案的优选决策过程

3.1 可视化工具对多目标方案的展示与初步决策

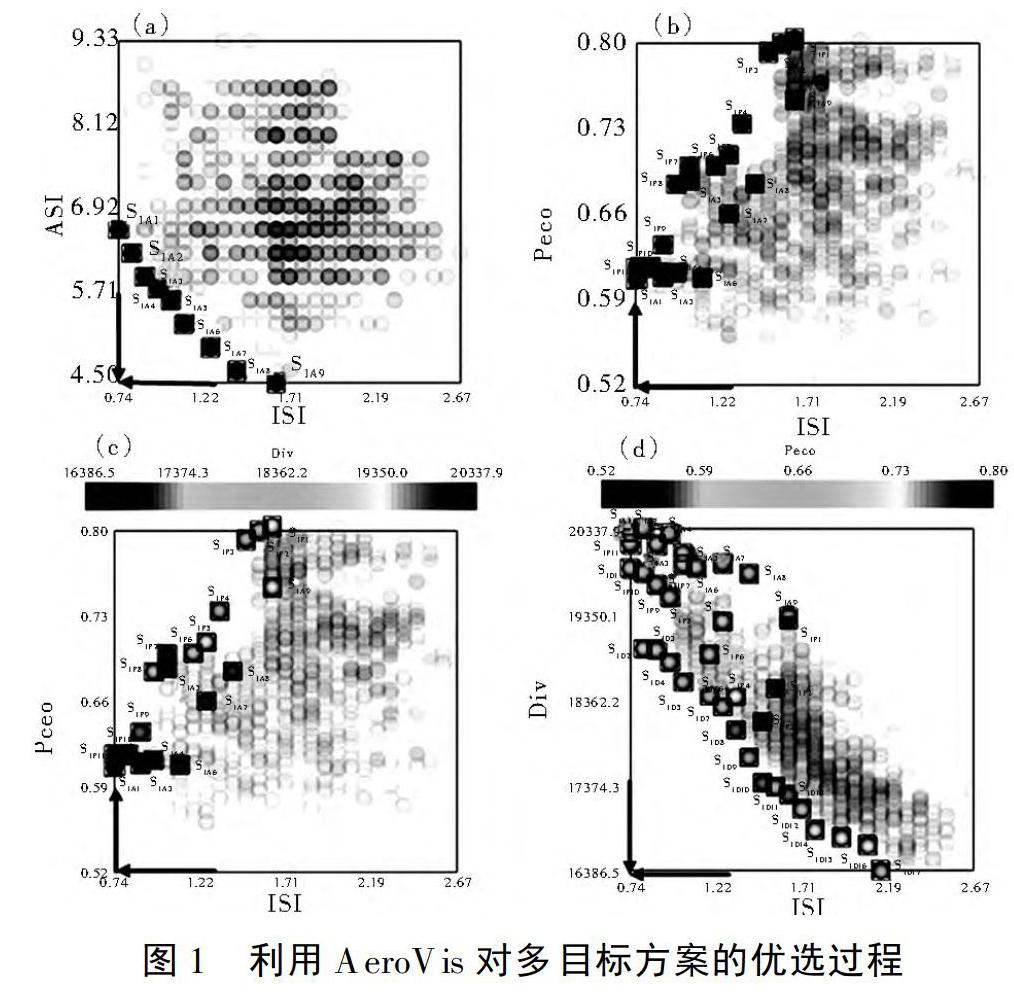
跨流域引水条件下，水库多目标调度模型生成的1 218个可行解，利用可视化分析工具AeroVis，对其进行两两目标间的非支配排序比较，得到经过可视化分析后的初次优选方案集，见图1。

图1中箭头方向表示各个目标函数的优化方向。ISI表示工业与生活缺水指数目标，ASI表示农业缺水指数目标，Peco表示生态整体满足度目标，Div表示引水量目标。其方案的优选过程如下。

3.3 基于模糊优选的方案再决策

在利用模糊语气算子对多目标方案进行优选的过程中，我们默认工业与生活供水目标，是4个调度目标中最为重要的目标，其目标权重值应大于其它3个目标。对于图1（1），由于初始决策只考虑了工业与生活、农业两个目标的权衡关系，因此，在利用模糊语气算子对不同目标进行赋权重值时，生态、引水量两个目标的重要性要差于工业与生活、农业两个目标，这里取极端的情况，即工业与生活目标比生态、引水量目标无可比拟重要。这样对于工业与生活、农业两个目标，利用模糊语气算子对其分别进行赋值试算，得到不同模糊语气算子下的方案模糊优选结果见表3。

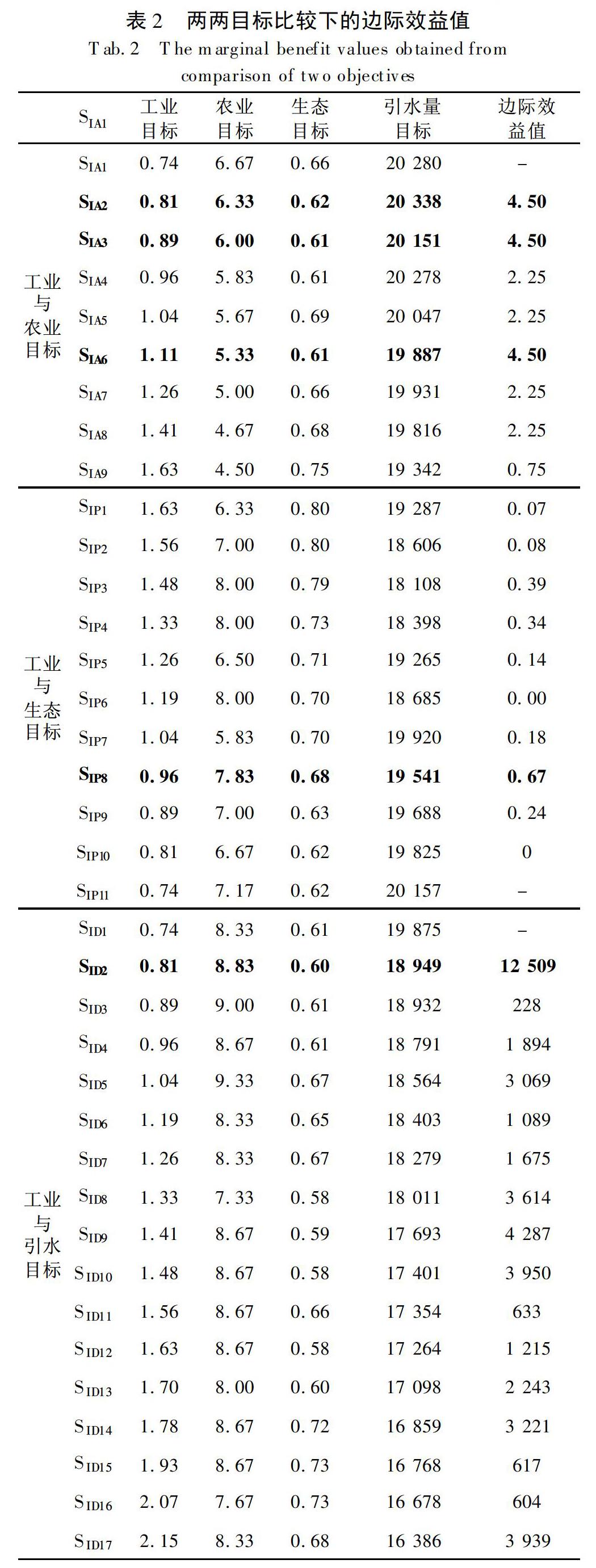
由表3可以看出，对于不用的工业与生活、农业目标模糊语气算子赋值，其最终的优选方案结果各不相同。当工业与生活目标比农业目标“同样”或“稍微”重要时，最优方案为SIA6，当工业与生活目标比农业目标“略为”、“较为”或“明显”重要时，最优方案为SIA3，当工业与生活目标比农业目标“显著”或“十分”重要时，最优方案为SIA2，而当工业与生活目标比农业目标“非常”、“极其”或“极端”重要时，最优方案为SIA1。对于工业与生活、农业两个目标，根据专家意见，认为其重要性程度为工业与生活目标比农业目标“非常”重要，因此，选择解SIA1作为考虑工业与生活、农业两个目标权衡下的参考解。

同理对于ISI和Peco，以及ISI和Div两个目标权衡下的参考解集，利用模糊语气算子进行目标权重赋值后，得到不同模糊语气算子下的方案优选结果见表4和表5。

对于工业与生活、生态两个目标，根据专家意见，认为其重要性程度为工业与生活目标比生态目标“显著”重要，因此，选择解SIP8作为考虑工业与生活、生态两个目标权衡下的参考解；而对于工业与生活、引水两个目标，根据专家意见，认为其重要性程度为工业与生活目标比引水目标“较为”重要，因此，选择解SID2作为考虑工业与生活、引水两个目标权衡下的参考解。

这样经过模糊优选方法的再次分析后，将由可视化工具初步决策得到的37个可行解，进一步分析决策得到SIA1、SIP8、SID2等3个可行解。

3.4 多目标方案的最终优选与决策

对于两两目标边际效益比较下得到的最优解SIA2、SIA3、SIA6、SIP8、SID2，作图见图2。

从图2可以看出，对于解SID2，其对于工业缺水指数和引水量两个目标，均是最优的，因此，选择解SID2作为边际效益分析下的最优决策方案。

而对于模糊优选得到的最优解SIA1、SIP8、SID2，作图见图3。

从图3可以看出，解SIA1对于工业缺水指数和农业缺水指数两个目标，均是最优的，因此，选择解SIA1作为模糊优选条件下的最优决策方案。

由于模糊优选得到的初始最优解集中，已包含了边际效益分析下的最优解SID2，而经过图3的分析，解SIA1优于解SID2。因此，将碧流河水库引水与供水条件下，水库的多目标调度的最优方案定为解SIA1。

4 结论

本文针对水库多目标调度模型生成的众多Pareto解决策困难的问题，利用可视化展示工具、边际效益分析、模糊优选等方法进行了逐步决策。首先利用可视化工具AeroVis，对多目标调度模型生成的繁多复杂可行解，通过目标间的两两决策，依次加入不同目标的决策信息，得到具有多个目标综合信息的初步优选决策集。随后利用边际效益分析的方法，对两两目标下，不同方案决策的边际效益做了分析，得到经过边际效益比较后的最优可行解集，同时利用模糊优选的方法，通过对不同目标比较间的模糊语气算子赋值，得到经过模糊优选后的最优可行解集。最后通过对最优解集的进一步分析，得到水库多目标调度的最终最优方案。通过不同的分析工具与决策方法，本文使多目标调度模型生成的众多Pareto可行解，经过层层决策后逐渐减少备选方案的数量，将决策方法与人的主观经验有效结合，逐渐降低多目标决策问题的复杂性。本文研究为多目标方案的优选决策提供一定的参考。

参考文献（References）：

[1] Von Neumann J，Morgenstern O.Theory of Games and Economic Behavior[M].Princeton：Princeton University Press，1944.

[2] Roy B.The Problems and methods with multiple objective function[J].Mathematical programming，1971，2（1）：239-266.

[3] Srinivas V，Shocker A D.Linear-programming techniques for multidimensional analysis of preferences[J].Psychometrika，1973，38（3）：337-369.[HJ2.02mm]

[4] Saaty T L.How to make a decision-the analytic hierarchy process[J].European Journal of Operational Research，1990，48（1）：9-26.

[5] Carrizonsa E，Conde E，Femandez F R.Multi-criteria analysis with partial information about the weighting coefficients.[J].European Journal of Operational Research，1995，2（81）：291-301.

[6] Yager P R.On the inclusion of importances in multi-criteria decision making in the fuzzy set[J].International Journal of Expert Systems：Research and Applications，1992，0（5）：211-228.

[7] 陈守煜，赵瑛琪.系统层次分析模糊优选模型[J].水利学报，1988（10）：1-10.（CHEN Shou-yu，ZHAO Ying-qi.The fuzzy optimum selecting model of system hierarchy analysis[J].Journal of Hydraulic Engineering，1988（10）：1-10.（in Chinese））

[8] 王本德，周惠成，程春田.梯级水库群防洪系统的多目标洪水调度决策的模糊优选[J].水利学报，1994（2）：31-39.（WANG Ben-de，ZHOU Hui-cheng，CHENG Chun-tian.Fuzzy optimizing approach to flood operation of multiobjective cascade reservoirs[J].Journal of Hydraulic Engineering，1994（2）：31-39.（in Chinese））

[9] 杨俊杰，周建中，李英海，等.基于模糊联系数的水库多目标防洪调度决策[J].华中科技大学学报：自然科学版，2009，37（9）：101-104.（YANG Jun-jie，ZHOU Jian-zhong，LI Ying-hai，et al.Multi-objective decision making on reservoir flood operation by using fuzzy connection numbers[J].Journal of Huazhong University of Science & Technology：Natural Science Edition，2009，37（9）：101-104.（in Chinese））

[10] 周晓光，张强，胡望斌.基于Vague集的TOPSIS方法及其应用[J].系统工程理论方法应用，2005，14（6）：537-541.（ZHOU Xiao-guang，ZHANG Qiang，HU Wang-bin.Research on TOPSIS methods based on vague set theory[J].Systems Engineering Theory Methodology Applications，2005，14（6）：537-541.（in Chinese））

[11] 李英海，周建中.基于改进熵权和Vague集的多目标防洪调度决策方法[J].水电能源科学，2010，28（6）：32-35.（LI Ying-hai，ZHOU Jian-zhong.Modified entropy method and Vague set based multi-objective flood control decision making approach[J].Systems Engineering Theory Methodology Applications，2010，28（6）：32-35.（in Chinese））

[12] Hamming R W.Numerical Methods for Scientists and Engineers[M].New York：McGraw-Hill，1962.

[13] Walker D J，Everson R，Fieldsend J E.Visualizing Mutually Nondominating Solution Sets in Many-Objective Optimization[J].IEEE Transactions on Evolutionary Computation，2013，17（2）：165-184.

[14] Blasco X，Herrero J M，Sanchis J，et al.A new graphical visualization of n-dimensional Pareto front for decision-making in multiobjective optimization[J].Information Sciences，2008，178（20）：3908-3924.

[15] Zio E，Bazzo R.A clustering procedure for reducing the number of representative solutions in the Pareto Front of multiobjective optimization problems[J].European Journal of Operational Research，2011，210（3）：624-634.

[16] 宋亚楠，仲茜，刘斌.基于边际效用函数的网络资源调度[J].电子学报，2013，41（4）：632-638.（SONG Ya-nan，ZHONG Qian，LIU Bin.Marginal utility function based networking resource scheduling[J].Acta Electronica Sinica，2013，41（4）：632-638.（in Chinese））

[17] 李翠梅，陶涛，刘遂庆.城市水价预测的长期边际成本方法理论与案例研究[J].资源科学，2010，32（7）：1356-1361.（LI Cui-mei，TAO Tao，LIU Sui-qing.A study on prediction of urban water prices based on the marginal cost methodology[J].Resources Science，2010，32（7）：1356-1361.（in Chinese））

[18] 邹进，张勇传.一种多目标决策问题的模糊解法及在洪水调度中的应用[J].水利学报，2003（1）：119-122.（ZOU Jin，ZHANG Yong-chuan.A fuzzy-logic-based approach to multi-objective decision making and its application in flood dispatching[J].Journal of Hydraulic Engineering.2003（1）：119-122.（in Chinese））

[19] Fu G.A fuzzy optimization method for multicriteria decision making：An application to reservoir flood control operation[J].Expert Systems with Applications，2008，34（1）：145-149.

[20] 陈守煜.可变模糊集理论与模型及其应用[M].辽宁：大连理工大学出版社，2009.（CHEN Shou-yu.Theory and model of variable fuzzy sets and its application[M].Liaoning：Dalian University of Technology Press，2009.（in Chinese））