基于自然邻点插值计算的溃堤洪水二维模型

苑希民 薛文宇 冯国娜 李培杰

摘要：为了模拟溃堤洪水的演进过程，建立计算区域的二维水动力模型，采用基于非结构网格的Roe格式离散求解。针对保护区内存在线状地物等实际特点，将道路、灌渠渠堤等建筑物线性处理，概化为宽顶堰的形式计算，赋予实际高程，将其作为特殊边界与非结构网格耦联；采用自然邻点插值计算方法，将保护区与排水沟分区插值，还原区域内排水沟地形，通过以上方法，获得了具有真实地形的模型。将模型应用于青铜峡河西灌区四排口险工溃堤洪水模拟，有效模拟了道路、渠堤等特殊边界阻水和桥涵过水效果，以及排水沟内排水和入河口洪水倒灌过程，较为真实地反映了洪水在计算区域内的演进过程和淹没范围，具有较好的应用价值。

关键词：二维模型；特殊边界；非结构网格；耦联；自然邻点插值计算；分区插值；青铜峡河西灌区

中图分类号：TV131.2 文献标志码：A 文章编号：1672-1683（2016）04-0014-07

Abstract：In order to simulate the flood wave propagation through the breaches，a two-dimensional hydrodynamic model was developed.Roe method of unstructured mesh was used to solve the 2D model.Based on the actual characteristics such as linear features in the flood protected zone，ways and irrigation ditches were generalized to broad crested weir for calculation and endowed real height，considering it as special border and coupled unstructured mesh.Using the Natural Neighbor Interpolation，separated interpolation was conducted between protected zone and aqueduct，and terrain of aqueduct in the area was recovered，and model with real terrain was obtained through the above methods.The model was applied to the case of Qingtongxia West Irrigation of Yellow River on Sipaikou，effectively simulated water blocking of special border such as ways and irrigation ditches and water flow of bridge culverts，and the effect of drain in the aqueduct and intrusion in the estuary，and truly simulated the flood wave propagation and inundation area of flood in calculation area，thus the paper has bright application value.

Key words：two-dimensional model；special border；unstructured mesh；coupled；natural neighbor interpolation；separated interpolation；Qingtongxia West Irrigation of Yellow River

近年来，由于河道中上游植被减少，导致流域涵养水源、调节径流、削减洪峰能力降低，加之水土流失加剧，河床淤高，泄洪能力降低，洪涝灾害的发生日趋频繁。在洪水冲刷的情况下，堤防一旦溃决，将造成房屋倒塌、农田绝收的严重后果。因此，对溃堤洪水在保护区域内的演进过程进行数值模拟，可以有效开展溃堤洪水的风险分析，为防汛救灾提供决策依据。

采用二维水动力学模型模拟溃堤洪水在二维平面上的演进情况，可以获得良好的模拟效果，近年来在国内外有着广泛的应用。求解二维模型最初采用有限差分法，有限元法和有限体积法等也被应用到二维水流数学模型的求解中。姜晓明等[1]采用基于黎曼近似解的水动力学模型对松花江干流胖头泡溃堤洪水进行了模拟计算；田志静[2]等根据洪水传播和运动的特性建立了二维水动力模型，并对沁河高庄段的水流进行了模拟；苑希民[3]等建立了漫溃堤联算的全二维水动力模型对黄河宁蒙段河道以及两岸的灌区进行了漫溃堤洪水的模拟计算；付成威[4]等利用建立的水动力模型模拟了谷堆圩蓄滞洪区溃堤洪水的演进过程；张弛[5]等将建立的二维数值模型应用到甘肃舟曲的山洪灾害模拟中，并采用了基于 leap-frog 有限差分格式的网格流出修正法来保证计算的稳定；Norton、King及Orlob[6]采用有限元算法求解水深平均的二维水动力学模型；Dushmanta et al[7]采用有限差分法的二维模型模拟了湄公河的漫顶洪水演进情况；Liang[8]等采用动态链接库技术，建立二维模型模拟了黄河东明段溃堤水流的演进过程；槐文信[9]采用有限分析法的二维水动力学模型，对渭河下游河道及洪泛区洪水进行了数值仿真模拟；蔡新[9]与谢作涛[10]分别建立了基于元胞自动机的洪水演进模型以及荆江洞庭湖洪水演进数学模型对洪水的演进进行了模拟张大伟[11-13]等利用水动力学模型对溃堤洪水在二维平面区域内的运动情况进行模拟。

保护区的实际地形直接影响洪水的演进过程，区域内道路、灌渠渠堤等特殊边界对洪水具有阻水作用，排水沟等沟道也会改变洪水的走向。本文将特殊阻水边界概化为宽顶堰，将其与非结构网格进行耦联，在耦联处加密剖分网格并赋予实际高程，使特殊边界具有真实地形；采用自然邻点插值算法对二维平面区域的网格分区进行插值，建立具有洪水倒灌及排水作用的真实沟道地形。基于以上地形数据，以二维浅水方程作为控制方程建立模型，将其应用于黄河青铜峡河西灌区，对四排口险工处溃堤洪水在保护区内的演进过程进行模拟。

1 数值模型

1.1 二维模型基本理论

溃堤洪水运动模拟的模型是基于Navier-Stokes方程沿水深平均的平面二维浅水方程，其表达形式为

1.2.2 几何位置耦联

利用实测的地理参考点线性连接成折线，实现道路、渠堤等特殊边界在非结构网格中的准确定位。在实际的计算过程中，相邻网格内的地理参考点连线与网格截面相交，获得了由相交的网格截面线构成的折线，模型将该折线定义为实际参与数值计算的折线，由此达到非结构网格与特殊边界的耦联，见图1。

1.3 自然邻点插值算法

1.3.1 算法原理

自然邻点插值方法是一种基于空间自相关性的面积权重线性内插法[18-19]，该方法是在Delaunay triangles网格和Voronoi图的基础上进行插值。Delaunay triangles网格和Voronoi图是一种互偶图形，对Delaunay triangles三角形网格的每一边做垂直平分线，就能得到Voronoi图，如图3中所示实线图。Voronoi cells即剖分的网格单元。对于单元中的节点而言，自然邻点定义为与其具有共同Voronoi cells边界的节点。

采用自然邻点插值法对计算网格进行插值，通过分区使各区域插值不受其它区域的插值影响，分别赋予不同区域实际高程，使模型能够充分反映计算区域内排水沟的真实地形，从而更准确地模拟洪水在保护区内的演进情况和排水沟内洪水倒灌或退水情况。

1.3.2 算法验证

（1）计算条件。

为验证采用自然邻点插值法分区插值后还原得到地形的准确性，本文选取黄河青铜峡河西灌区内第三排水沟在灌区内4.95 km²的保护区为例进行验证。第三排水沟位于灌区北部，青石段实测大断面第42和43断面之间，沟宽52 m，长3 047 m，沟道纵深3.6 m。采用非结构三角形网格对二维计算区域进行剖分，网格边长设置为300 m，在第三排水沟处采用100 m边长的网格对其加密剖分，共剖分网格数量431个，利用自然邻点插值算法对保护区和排水沟分区进行插值。

（2）插值结果验证。

图5和图6分别是对插值结果验证得到的结果图。图5为采用自然邻点插值算法在不同条件下插值所得的结果，对分区插值的效果进行了验证。图5（1）利用了分区插值的方法对第三排水沟所在的区域进行插值，图中线条代表计算区域的等高线，可以在图中看到清晰完整的第三排水沟的轮廓，且从分布较密的等高线处可以观察到排水沟堤防边坡较为均匀的高程变化情况。而图5（2）未采用分区插值的方法，在插值过程中，保护区与排水沟的高程点相互影响，不能获得真实完整的排水沟地形，未能在图中显示出排水沟的轮廓。

图6是提取在不同条件下插值从模型中提取的沟底各点高程，图中显示采用分区插值的方法获得的沟底高程从高至低较为均匀的变化，最后趋于稳定，这与第三排水沟所在保护区的实际地形相符，沟底的高程并没有较大的起伏。未采用分区插值的方法获得的沟底高程，在模型中存在较大的起伏，这是由于未进行分区插值时保护区与排水沟的高程数据相互影响，沟道网格的高程部分区域被抬高，这与第三排水沟的实际地形并不相符。因此，通过以上验证可知分区插值可以还原模拟区域真实的地形，计算结果更具有真实性。

2 模型应用

2.1 模拟区域概况

黄河青铜峡河西灌区总面积4 283.8 km²，灌区从南至北，涉及青铜峡市、永宁县、银川市、贺兰县、平罗县和惠农区，一旦溃堤，将会造成严重的经济损失。石嘴山市平罗县的四排口险工段位于黄河转弯处，河道接近90°大弯，主流直冲左岸，直接威胁大堤，堤后大量耕地，下游为平罗县城，溃堤后会对下游造成较大的影响。本文选择四排口险工作为溃口位置，对灌区内平罗县、惠农区所在约322 km²的灌区作为计算区域进行溃堤洪水模拟。

2.2 模型计算条件确定

2.2.1 一维模型

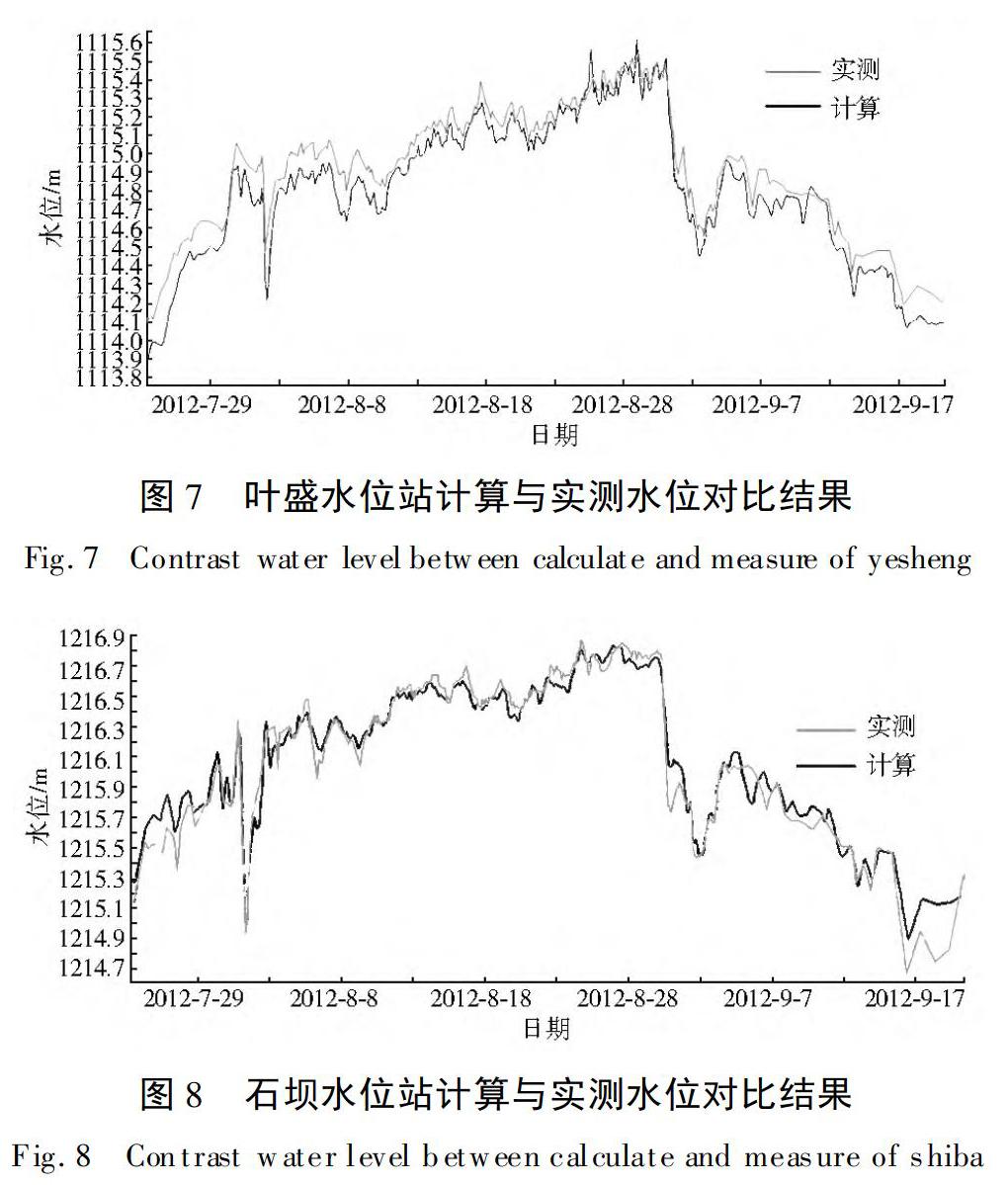
一维河道总长度195 km，以青铜峡水文站和石嘴山水文站为上下控制边界，利用河道上45个实测大断面建立模型。选取2012年8月实测洪水过程，并根据叶盛水位站和石坝水位站的实测水位数据，进行参数率定和模型验证。率定结果显示，水位误差范围为0.004～0.196 m，一维模型准确合理。叶盛水位站与石坝水位站水位率定结果见图7和图8。

采用2012年洪水过程作为典型年洪水，按同倍比放大方法获得青铜峡站100年一遇洪水流量过程，作为一维模型上边界条件，下边界条件为石嘴山站水位-流量关系，计算时间步长为30 s，每1 h输出一次计算结果。

2.2.2 二维模型

采用非结构三角形网格对灌区内面积为322 km²的计算区域进行剖分，网格边长设置为300 m，对道路、渠堤等特殊边界以及计算区域内的排水沟采用100 m边长的网格加密剖分，剖分网格数量64 382个，计算节点32 627个。

二维模型溃口设置为水位边界，堤防溃决时刻为河道水位达到堤防设计水位时，水位降落至堤后地面高程时停止分洪。通过调查历史溃堤记录，结合河势、河宽及水头差等因素，确定溃口宽度为100 m。按照研究区域的土地利用情况进行糙率分区：村庄0.1；农田耕地0.04；湖泊等水域0.035。设置干湿边界条件：干水深0.005 m，湿水深0.09 m。模型计算时间步长为30 s。

2.3 特殊边界概化

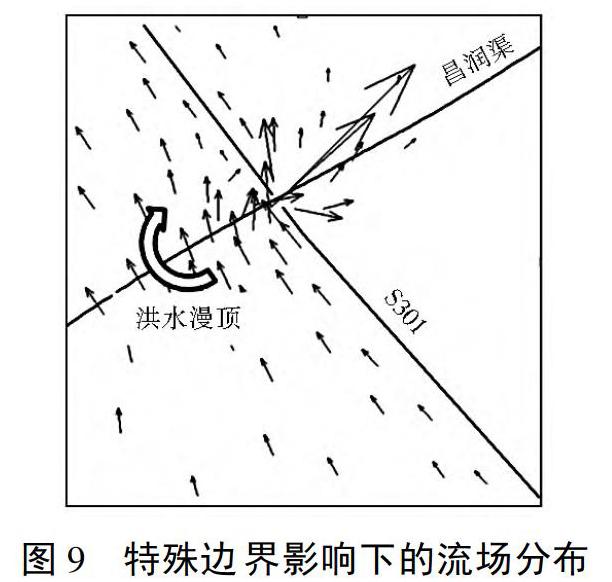
通过实地测量，获得道路、渠堤等特殊边界的地理坐标与高程参数，将其线性连接，实现特殊边界在模型中的准确定位。利用非结构网格与特殊边界耦联的方式，概化出特殊边界在模型中的真实地形，并按照洪水在边界处漫顶与否，进行洪水计算。本次计算区域中具有阻水作用的特殊边界包括惠农渠、昌润渠、滂渠、京藏高速、G109和S301，根据过水桥涵的位置将道路分段，建立具有真实地形的模拟区域，模拟计算区域内的道路阻水及桥涵过水效果，达到模拟效果的真实性。

2.4 分区插值

计算区域内存在第三排水沟、第五排水沟，是青铜峡河西灌区内具有排水作用的两条沟道。在上游发生溃堤的情况下，当洪水从上游演进至排水沟时，部分洪水进入排水沟内沿沟道流动；与此同时，由于下游河道水位顶托，排水沟入河口处发生洪水倒灌，洪水沿沟道倒流入灌区内，并且漫溢对两岸造成淹没影响。

将保护区与排水沟分区剖分网格。根据设计资料，提取第三、第五排水沟各断面的地理坐标与沟底高程，并按照100 m的距离内插；保护区内各离散点的地理坐标与高程数据通过提取DEM获得。采用自然邻点插值法将提取到的数据分别赋予到保护区与排水沟的计算网格中，获得沟道的真实地形，模拟洪水在排水沟内退水及倒灌效果，达到模拟效果的真实性。

2.5 计算结果分析

图9为线状地物及桥涵影响下的流场分布图，洪水演进至S301时，水位未超过S301路面的高度，路面未过流，不存在动量交换，洪水沿着S301路基演进至昌润渠时刻，洪水因其水位超过昌润渠渠堤而漫过灌渠堤顶。由于昌润渠从S301路下穿过，道路上存在30 m的过水桥涵，从图中的流场分布中可以看出明显的过水效果。在洪水演进至昌润渠与S301交界处，由于受到路基与渠堤的阻水而出现雍水现象，道路上虽然存在过水桥涵，但过水能力有限，洪水不能完全通过，在渠堤与路基交界处雍水越多，水头越大，当水位超过渠堤高程时水流瞬间释放至堤后，因此存在较大的流速。

图10为第五排水沟上游沟道内排水的流场分布图，图11为第五排水沟下游入河口处发生洪水倒灌的流场分布图。第五排水沟沟底高程低于两岸保护区3～4 m，当洪水在保护区内演进至第五排水沟时，部分水流进入排水沟，并沿沟道一直向入河口方向演进，图13可以看出洪水沿沟道的演进效果。与此同时，由于上游100年一遇洪水致使黄河水位上涨，下游排水沟入河口处受黄河水位顶托，高水位的洪水沿排水沟向上游演进，发生洪水倒灌现象，图14可以看到明显的洪水倒灌效果。

选取S301省道，对加入特殊边界及未加入特殊边界两种情况下水位的过程进行对比来说明模型的精度。并以第五排水沟为例，利用两种不同的插值条件下水位过程对比的结果来说明模型还原地形的真实性。图12是S301路前某一地理参考点在整个模拟时段的水位过程，图中数据对比可知，由于S301省道的阻水作用，使路前存在积水现象，该点计算的水位值较未加入特殊边界的模型计算所得数值高，符合实际的情况。图13是第五排水沟内某一地理参考点在整个模拟时段的水深过程数据，在起算时刻沟内存在一定的水深值，计算的过程中由于上游洪水演进至沟内，以及下游沟道入河口处发生的洪水倒灌，使排水沟内水位上涨。由图中对比可知，在分区插值情况下，该点计算的水深值较未插值计算所得的水深值大，符合实际情况。

图14为青铜峡河西灌区四排口溃堤后，保护区不同时刻的淹没水深图。由图可以看出，四排口险工发生溃堤，导致洪水在灌区内向下游低洼地区演进，形成较大的淹没范围，下游入河口处洪水进入第三、第五排水沟内形成倒灌，并且漫溢对两岸村庄造成淹没。通过影响分析，洪水淹没面积为315.36 km²，最终积水量1.45亿m³，受灾人口5.32万人，其中农田淹没面积23 375.64 hm²，房屋淹没面积886.02万m²。通过模拟洪水的演进过程，可知尾闸镇、黄渠桥镇、渠口乡、庙台乡受灾严重，应作为防汛重点关注区域，该结果为防汛部门的应急管理措施提供了技术支撑。

3 结论

本文针对溃堤水流的特点，建立了二维水动力模型，对保护区内溃堤洪水的演进过程进行模拟。通过将道路、渠堤等线状地物概化为宽顶堰计算，赋予实际高程，并作为特殊边界与非结构网格耦联，使特殊边界具有真实的地形；此外，保护区内存在的排水沟具有排水作用，从而改变了洪水在排水沟处的流场分布，文中采用自然邻点插值计算方法对计算区域进行分区插值，将排水沟真实地反映在模型中。采用该模型对青铜峡河西灌区四排口险工溃堤洪水进行模拟，模型还原了区域的真实地形，对线状地物阻水、桥涵过水以及沟道排水和洪水倒灌具有良好的模拟效果。因此，模型可有效模拟溃堤洪水演进过程，具有较好的应用价值。

参考文献（References）：

[1] 姜晓明，李丹勋，王兴奎.基于黎曼近似解的溃堤洪水一维-二维耦合数学模型[J].水科学进展，2012，23（2）：214-221.（JIANG Xiao-ming，LI Dan-xun，WANG Xing-kui.Coupled one-and two-dimensional numerical modeling of levee-breach flows using the Godunov method [J].Advances in Water Science，2012，23（2）：214-221.（in Chinese））

[2] 田志静，冯民权，赵明登.沁河高庄段洪水漫堤二维模拟.[J].武汉大学学报，2013，46（4）：414-422.（TIAN Zhi-jing，FENG Min-quan，ZHAO Ming-deng，2D simulation of dike overtopping in Gaozhuang reach of Qinhe River [J].Engineering Journal of Wuhan University，2013，46（4）：414-422.（in Chinese））

[3] 苑希民，田福昌，王丽娜.漫溃堤洪水联算全二维水动力模型及应用.[J].水科学进展，2015，26（1）：83-90 .（YUAN Xi-min，TIAN Fu-chang，WANG Li-na.Comprehensive two-dimensional associate hydrodynamic models for overflow and levee-breach flood and its application [J].Advances in Water Science，2015，26（1）：83-90.（in Chinese））

[4] 付成威，苑希民，杨敏.实时动态耦合模型及其在洪水风险图中的应用.[J].水利水运工程学报，2013，5：32-38.（FU Cheng-wei，YUAN Xi-min，YANG Min.A real-time dynamic coupling model for flood routing and its application to flood risk charting.[J].Hydro-science and Engineering，2013，5：32-38.（in Chinese））

[5] 张弛，张家华，王浩.基于网格流出修正法的山洪演进数值模拟.[J].河海大学学报：自然科学版，2014，42（2）：107-113.（ZHANG Chi，ZHANG Jia-hua，WANG Hao.Numerical simulation of flash flood routing based on grid outflow correction method[J].Journal of Hohai University：Natural Sciences，2014，42（2）：107-113.（in Chinese））

[6] Donnel，Barbara，Letter P，et al.Users Guidefor RMA2 Version 4.5[M].US Army Engineer Research and Development Center，2005：1-98.

[7] Dushmanta D，Jahangir A，Kazuo U，et al.A two-dimensional hydrodynamic model for flood inundation simulation：a case study in the lower Mekong river basin [J].Hydrological Progresses，2007，21：1223-1237.

[8] Liang D，Falconer R A，Lin B.Linking one-and two-dimensional model for free surface flows[J].Proceedings of the Institution of Civil Engineers-Water Management，2007，160（3）：145-151.

[9] 槐文信，赵振武，童汉毅，等.渭河下游河道及洪泛区洪水演进的数值仿真（I）—数学模型及其验证[J].武汉大学学报，2003，36（4）：10-14.（HUAI Wen-xin，ZHAO Zhen-wu，TONG Han-yi，et al.Numerical simulation on flood in downstream of Weihe River and flooded area（I）-M athematic model and its calculation method.[J].Engineering Journal of Wuhan University，2003，36（4）：10-14.（in Chinese））[ZK）]

[10] CAI Xin，LI Yi，GUO Xing-wen，et al.Mathematical model for flood routing based on cellular automaton [J].Water Science and Engineering，2014，7（2）：133-142.

[11] XIE Zuo-tao，YANG Fang-li；FU Xiao-li.Mathematical model for flood routing in Jingjiang River and Dongting Lake network [J].Water Science and Engineering，2012，5（3）：259-268.

[12] 张大伟，李丹勋，陈稚聪，等.溃堤洪水的一维、二维耦合水动力模型及应用[J].水力发电学报，2010，29（2）：149-154.（ZHANG Da-wei，LI Dan-xun，CHEN Zhi-cong，et al.Coupled one-and two-dimensional hydrodynamic models for levee-breach flood and its application [J].Journal of Hydroelectric Engineering，2010，29（2）：149-154.（in Chinese））

[13] LAI X，JIANG J，LIANG Q，et al.Large-scale hydrodynamic modeling of the middle Yangtze River Basin with complex river-lake interactions [J].Journal of Hydrology，2013，492：228-243.

[14] 陈文龙，宋利祥，刑领航，等.一维—二维耦合的防洪保护区洪水演进数学模型[J].水科学进展，2014，25（6）：848-855.（CHEN Wen-long，SONG Li-xiang，XING ling-hang，et al.A 1D—2D coupled mathematical model for numerical simulating of flood routine in flood protected zone[J].Advances in Water Science，2014，25（6）：848-855.（in Chinese）

[15] Murillo J，Burguete J，Brufau P，et al.Coupling between shallow water and solute flow equations：analysis and management of source terms in 2D [J].International Journal for Numerical Methods in Fluids，2005，49：267-299.

[16] 刘刚，金生.基于修正Roe格式的有限体积法求解二维浅水方程[J].水利水运工程学报，2009（3）：29-33.（LIU Gang，JIN Sheng.Finite volume model for the 2D shallow water equations using modified Roe scheme [J].Hydro-Science and Engineering，2009（3）：29-33.（in Chinese））

[17] 张大伟，王兴奎，李丹勋.建筑物影响下的堤坝溃决水流数值模拟方法[J].水动力学研究与进展，2008，23（1）：48-54.（ZHANG Da-wei，WANG Xing-kui，LI Dan-xun.Numerical modeling of dam-break flow under the influence of buildings[J].Journal of Hydrodinamics，2008，23（1）：48-54.（in Chinese））

[18] 董闯，刘九夫，谢自银，等.面降雨量在确定河流干支关系中的应用[J].水电能源科学，2013，31（5）：5-8.（DONG Chuang，LIU Jiu-fu，XIE Zi-yin，et al.Application of areal precipitation in determination of streams relationship[J].Water Resources and Power，2013，31（5）：5-8.（in Chinese））

[19] 张伟，覃庆炎，简兴祥.自然邻点插值算法及其在二维不规则数据网格化中的应用[J].物探化探计算技术，2011，33（3）：291-295.（ZHANG Wei，QIN Qing-yan，JIAN Xing-xiang.Natural curvature splines and application of 2D irregular data mesh[J].Computing Techniques for Geophysical and Geochemical Exploration，2011，33（3）：291-295.（in Chinese））