一节数学课上关于分类讨论思想的学习
2016-07-09
(呼和浩特市土默特学校,内蒙古 呼和浩特 010010)
在《新课程标准》中关于基本理念的叙述中指出:数学是人们生活、劳动和学习必不可少的工具;数学为其他科学提供了语言、思想和方法,是一切重大技术发展的基础;数学在提高人的推理能力、抽象能力、想象力和创造力方面有着独特的作用。分类思想,在我们的实际生活中经常用到,比如学生对书籍或一些物品的整理,教科书上对各章节的划分……。通过分类处理,可以让事物变得更有条理性,事物之间的关联更加的清晰,而分类讨论的能力也可以让我们的逻辑思维更清楚,分析问题的能力得到训练。
根据新课程标准的要求,通过初中数学的学习,学生对方程、类比、分类讨论、建模等数学思想方法应有一定的感知,并能在解题过程中进行应用,这是对学生提出的较高学习要求。就这些概念本身而言的是比较抽象,也并不要求学生对概念进行记忆。因此,学生只有在新知识的习得过程中、知识的应用中去体会、感悟它们,才能理解并掌握。
分类讨论的思想方法,它一直贯穿于初中数学知识。从教材内容的安排上来看,初中数学知识分代数、几何、概率、统计四大部分,采用不同的方法进行研究,从各部分内容来看,如代数中实数的分类、式的分类、方程的分类、函数的分类等,这都是分类思想的表现。通过了解学习内容,让学生在初中的第一堂课就感受当数学思想方法的运用,同时,通过学习内容的分类,使学习的难度有了一定的层次,每一节内容的学习目标更具体,便于生对知识的掌握。
初中数学内容中分类讨论的思想主要表现在以下几个方面:母系数或绝对值符号的运算,如,解方程 ax>1时,应分为:当a>0时(1)含字当a<0时,一次函数的截距和斜率对图象位置的影响,如,一次函数y =kx +b,当 k>0,b>0 时,图象过一、二、三象限,当 k>0,b<0 时,图象过一、三、四象限,当 k<0,b>0 时,图象过一、二、四象限,当 k<0,b<0 时,图象过二、三、四象限,由于字母系数的取值和绝对值符号去掉后会有不同结果,因此需要分类讨论。(2)一些概念和定理的论证过程包含了多种情况,如,三角形按边长分类为:
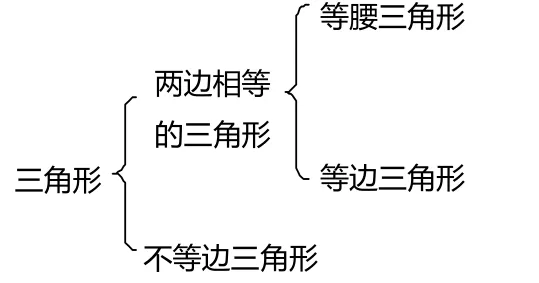
还有角的分类,多边形的分类,圆周角定理的证明等。(3)有些数学问题,尽管结果一样,但由于每种结果的分类依据不同,也要分类讨论,如,有理数可按定义分为:
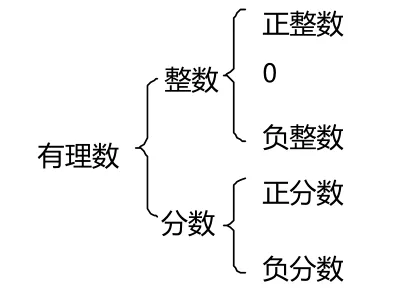
在人教版八年级上《等腰三角形》的一次习题课中,学生碰到了这样一些问题:
1、一等腰三角形的一个底角是40°,求另外两个角的度数。
2、一等腰三角形的一个顶角是40°,求另外两个角的度数。
3、一等腰三角形的一个内角是40°,求另外两个角的度数。
前两个问题学生能够很快地找出答案,但在回答第三个问题时,一部分学生有了质疑:这个已知的角是顶角还是底角?通过讨论,学生很快分析得出,这个角可能是顶角,也可能是底角。因此,这里有两种情况。通过这几个练习让学生初步体会到分类思想的用途。
4、一等腰三角形的一个内角是100°,求另外两个角的度数。
5、一等腰三角形的两边分别是6,3,求这个三角形的周长。
6、已知等腰三角形的周长是24,一边长为6,则另两边的长是多少?
7、已知等腰三角形的周长是24,一边长为10,则另两边的长是多少?
有了前面的问题做铺垫,学生很自然的在处理这两个题目时都会进行分情况(分类)处理,但会发现有些情况是不符合题意的,应当舍去。
8、一等腰三角形的周长是16,两边之差为2.求它的三边长各是多少?
通过思考,学生们很快就提出了解法:
①设腰长为x,则:x+x+x+2=16,解得:x=。三边长分别为,,。
②设底边长为x,(x-2)+(x-2)+x=16,解得:x=。三边长分别为,,。
这是出现了两种相同的结果。问题出在哪儿?
经过讨论,又有学生提出:
③设腰长为x,则:x+x+x-2=16,解得:x=。三边长分别为6,4。
④ 设腰长为 x,则:(x+2)+(x+2)+x=16,解得:x=。三边长分别为。
再次出现了同样的问题。通过学生几分钟的观察思考,就有学生发现了问题所在:这四种解法中实际上就包含了两种情况:①底边比腰长多2;②腰长比底边多2。因而,分类不应该是以设不同的量(腰或底)为依据来进行求解。
到这里,一个教学环节结束,让学生们回过头再来看看这几个问题给大家带来的注意点,不难得出:
(1)在几何知识中,我们也会遇到分类讨论的问题,即:问题的答案不唯一;
(2)在分类的几种情况总,允许有不合题意的结论被排除;
(3)分类时,一定要找准分类的依据,以便做到不重不漏。
当然,分类讨论思想的应用在后继的学习中还会出现,要能准确应用,要求学生具有较强的分析、整理能力和严密的逻辑思考。这一能力的养成,并不是一节课就能够达到的,需要通过一定量练习的点滴渗透、积累、概况和归纳才能形成,这也是初中阶段学习应养成的一种数学能力,在教学过程中不容忽视。
[1]数学课程标准研制组编写.全日制义务教育数学课程标准(实验稿)解读.北京:北京师范大学出版社,2002.5.第1版
