“烙饼”的数学建模和教学逻辑

吴　飞

（尤溪教师进修学校，福建尤溪365100）



“烙饼”的数学建模和教学逻辑

吴飞

（尤溪教师进修学校，福建尤溪365100）

摘要：烙饼问题是统筹、优化的问题，也是烙饼次数及每烙一次的时间和总时间构成的线性关系问题。教材编排侧重优化手段得到烙饼的最省时间，对此，也有必要通过数学建模，通过设计每次最多只能烙2张饼的最省时间和饼数（面数）关系表做出数学化回应。在此基础上，根据优化和抽象结果，对教学逻辑做出具体安排和说明。

关键词：烙饼问题；统筹优化；数学建模；教学逻辑

“烙饼”问题是人教版小学四年级上册教材第八单元“数学广角——优化”中的教学情境内容。与旧版相比，新版教材将“烙饼问题”调整到了第一部分的“沏茶问题”之后。根据同版教材的教师用书介绍，这样的调整是“基于学生的认识水平及实验教材的实践经验”，体现“3个例题的编排顺序由浅入深，层次清晰，符合学生的认知水平和思维水平，有利于学生理解和体会数学思想”的特点。

优化的前提是统筹，而且统筹过程的本质是各种数量关系和空间形式的逻辑疏理，也是一种推理和建模过程。只是这种过程涉及到分析、预测、筹划、运筹（实施）和平衡（比较）等较为复杂的环节。所以，运筹到位优化选择才有可能。因此，教材试图通过沏茶、烙饼、赛马的统筹推进以使学生感受并初步理解优化的数学思想，是符合逻辑期望的。

基于此，笔者以为有必要在不少优秀教师演绎“烙饼问题”的教学之后，对“烙饼问题”的数学内涵进行教学的再思考。

一、烙饼问题的数学建模

为了看清烙饼问题的数学本质，我们先从特殊的情况：每次只能烙一张饼，每面3分钟开始分析。

一张一张烙的实质就是一面一面地烙。所以，有几个面就要烙几次，显然，“一张饼有2个面，每个面要烙3分钟”是问题的本质。由此可以得到：烙n张饼的时间就是n张×2面×3分钟=6n（分钟）。

现在来分析每次最多只能烙2张的情况。

“每次最多可以烙2张”的实际意义是每次可以烙1个面也可以同时烙2个面，而且同时烙2个面的时间和单烙1个面的时间是相同的。由此，思考怎么烙饼的问题就转变成只要统筹解决“总共要烙几个面”“每次要烙几个面”就行了。回到具体看：1张饼要烙多少时间？因为正反2个面不能同时烙，所以只能一个面一个面地烙。此时，锅的空间是处在自然浪费的状态，所费时间是2面×3=6分钟。2张饼呢？如果是1 张1张来就是4面×3=12分钟；如果是2张一起来就是4面÷2×3=6分钟。3张饼呢？1张1张烙就是6面× 3=18分钟；先烙1张后烙2张就是2面×3+4面÷2× 3=12分钟；先烙2张后烙1张是4面÷2×3+2面×3= 12分钟；如果是每次都烙2面——第一张和第二张饼同时烙一面，接着第一和第三张再同时烙一面，然后是第二和第三张最后再同时烙一面，所要的时间就是6面÷2×3=9分钟。4张呢？可以一张张烙24分钟；一张再一张烙后两张烙或两张烙后再一张一张烙18分钟；一张烙完再按三张的烙法或按三张烙法再烙一张15分钟；每次烙两面四张饼只要12分钟。5张以后烙的方式有所不同但思维一样。显然，不管是1张1张来还是2张2张烙，所要花费的时间只与“所要烙的总面数”有关。至于是单烙还是双烙那是策略问题。

从以上分析，可以得到这样一个结论：烙一次的时间（t）和烙饼的次数（c）共同构成了烙饼总时数（s）的一个线性关系s=ct，当烙一次的时间确定，根据自变量c（烙的次数：一面一次、两面一次）的取值范围：饼数≤c≤总面数（一块饼的情况除外），因此，因变量s是可以取到最大值和最小值的。

每次最多只能烙三张的情况与此相仿，不同的只是烙的次数c可以是一面一次、两面一次和三面一次，而要让锅不闲置，操作方式要实行交叉烙法而已（只要弄清楚4块饼的情况即可：一次烙三面交替烙第三、四块饼，只要烙三次）。在这种情况下，烙的次数c的取值范围：饼数除以3（整除）≤c≤总面数，或者是：饼数除以3（不整除）加1≤c≤总面数。

二、烙饼问题的教材分析

教材中，烙饼的情境问题是以“怎样才能尽快吃上饼”做为问题解决的标准。

对学生而言，无论是生活经验还是知识储备，解决问题的基础不应该有大的困难。从生活经验讲，大部分的学生是知道烙饼要一面一面地进行；从知识角度看，学生很容易就会用乘法来计算烙饼的时间。

所以，教材的教师用书建议：一要“给学生提供探索的空间”：独立思考、小组交流，然后是比较方案；二要“在‘悟’中明确规律”：怎么省时？省时的关键是什么？在此基础上让学生探索烙4张，5张……

从“能探索分析和解决简单问题的有效方法，了解解决问题方法的多样性”的要求看，教材提供的教学思路是可行的、明了的。

虽然，这是一节统筹优化的探究课，只要引导学生筹划实施每一个方案，然后再行对比和选择（也是合情推理），就能得到“用时9分钟是最少的”优化结果。而且我们也知道，对优化思想应用的体会和感悟本身就是这节课的教学目标之一。但是，为什么用时9分钟是最少的？有没有可能是8分钟甚至更少？我们会不会出现漏掉方案的情况？怎么才能保证结论是严谨的、唯一的？这些问题仅仅通过动手操作似乎总不让人放心。对此，笔者以为有必要作出更数学化的回应。只是这种回应在课堂的具体教学中要实施到何种程度需要商榷。

下表就是具体回应的数学化过程表。

每次最多只能烙2张饼的最省时间和饼数（面数）关系表

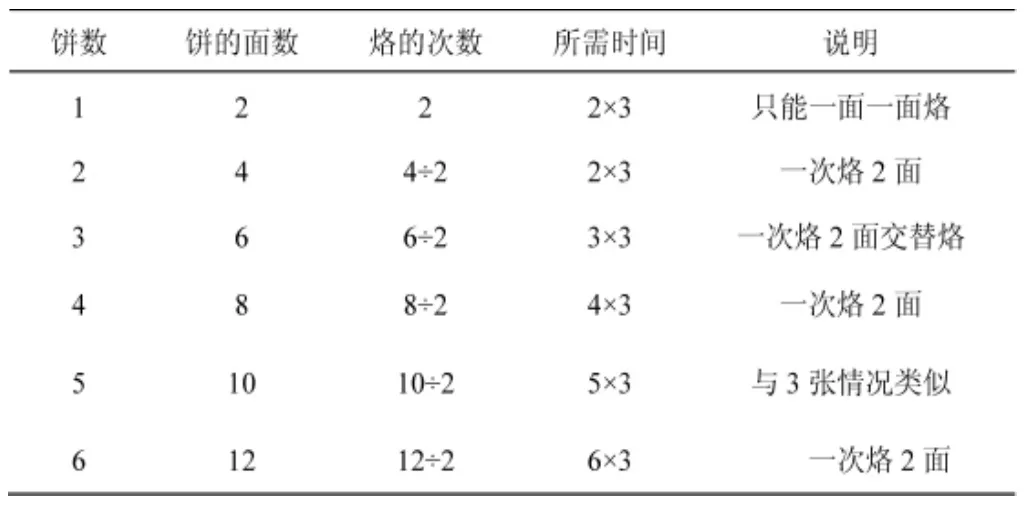
上表中一目了然的信息有：一次烙1面和一次烙2面时间一样；每次烙2面锅才不会闲着——这就是“尽快”的现实意义。但是本表更重要的信息是：烙饼所要花费的时间只与所要烙的总面数有关。3张饼有6个面，每次烙2面，必须要烙3次才能完成任务。所以，费时要且只要3×3=9分钟。

到此，我们既解决了烙饼方案多样性的问题，更解决了用时最少的确定性问题。所以，只有将统筹和抽象、数学建模结合在一起，这样的优化才是数学化视野下的数学基本活动（经验）。

三、烙饼问题的教学逻辑

鉴于以上分析，烙饼的教学过程可以遵循以下活动逻辑。

1.理解问题情境，明白需要解决的问题

教师在这个环节的基本任务是引导学生读图并弄清以下信息：要烙几块饼、每张饼2面都要烙、每面要烙3分钟、每次最多只能烙2张。与此同时，提出问题并板书：怎样才能尽快吃上饼？在此环节中教师最好做个“会不会烙饼”的经验调查，防止没有生活经验的学生出现经验性思维障碍而影响后续思维活动。

2.动手操作，独立思考

让学生自主地去理解“尽快”的含义，独立地去经历烙饼的过程（程序），主动地去设计烙饼的方案并计算出每个方案需要的时间。给够时间和空间让学生尽情地去体会求异、求优的优化思想，体验问题解决策略的多样性，以积累基本活动经验。

3.小组交流，相互完善

带着以下问题开展小组讨论：（1）烙好一张饼要烙几个面？（2）三张饼有几种不同的烙法，请列出具体步骤。（3）每次烙1张饼和烙2张饼所花费的时间一样吗？（4）要尽快烙好3张饼最重要的问题是什么？（5）你能把自己认为最省时的烙法演示给同伴吗？（6）你能计算出每一种烙法的时间吗？

4.小组汇报展示，教师追问

请不同的小组分别汇报以上6个问题。在每个小组汇报时教师要适时地刨根问底。例如：你说四种哪四种？能够再具体点吗？为什么一张一张烙最慢？一次烙1张和一次烙2张为什么时间一样？要烙的快最重要的是什么？你是怎么计算出时间的？通过追问引导学生疏理自己的思维过程，初步实现思维从发散到收敛再到优化。

5.思维碰撞，探究关系

提出问题：（1）有人超过18分钟吗？为什么？（总共只有6个面，要超的话准烧焦。）（2）烙1张饼最少是6分钟，为什么？那么烙2张饼最少烙几次？（3）4张饼有几个面？每次烙2面要烙几次？（4）3张饼几个面？每次可以烙2个面吗？可以的话至少要烙几次？

列出每次最多只能烙2张饼的最省时间和饼数（面数）关系表。之后请学生写出烙5张和7张的最省时的烙法并列出计算式。

“烙饼问题”“打电话问题”和“找次品问题”都是统筹、优化问题。烙饼的关键是不让锅闲着，打电话的关键是不让已接电话的人闲着，找次品的关键是让天平的每一次使用发挥最大效果［2］。从某一问题出发而能够触及同类问题的思想是教学的永恒追求。优化思想的思维本质是求异、求优，求异的前提要多样化（正如烙饼的方式多样），求优的前提则是比较；没有多样化不可能有层次，没有比较不可能优化。在教学中，相对于结论而言我们更重视对获得结论的理解，对结论的发展和深化,更重视对目标内涵中所蕴含条件和标准的理解。所以，只有对“烙饼问题”作出数学化回应并建模，才能让同类问题的表现形式更加简明，教学更加有效。

参考文献:

［1］郑毓信.“优化问题”与“优化思想”［J］.教学月刊（小学版），2013（7，8）.

［2］张卫星.研读数学教材的四个维度——以人教版数学四年级上册“烙饼问题”为例［J］.教学与管理，2015（14）.

［3］张小燕.让学生触摸问题的本质——“烙饼问题”的教学重构与思考［J］.教育科研论坛，2011（03）.

中图分类号：G633.6

文献标识码：A

文章编号：1673-9884（2016）02-0061-03

收稿日期：2015 - 11 - 15

作者简介：吴飞（1963-）男，福建尤溪人，尤溪教师进修学校高级教师。