讨论激荡思维 交流促进发展——记一次备课组活动过程及其意义

王世荣

(江苏省金湖中学，211600)



○数学教育○

讨论激荡思维交流促进发展
——记一次备课组活动过程及其意义

王世荣

(江苏省金湖中学，211600)

备课组活动是同学科教师开展教学研究的一种活动形式,它是优化教学工作的载体,是教学资源共享的途径,是教师协同发展的摇篮,是提高专业素养的温室．备课组活动所承载内容多种多样,可能是对教学工作计划的分配;可能是对教学设计的讨论,亦可能是对某一问题的集体思考．本文以一道检测题的讨论过程为例,说明备课组活动的重要意义．

(1)求椭圆的标准方程;

(2)如图1，取垂直于x轴的直线与椭圆相交于不同的两点P,P′,过P,P′作圆心为Q的圆,使椭圆上的其余点均在圆Q外,若PQ⊥P′Q,求圆Q的标准方程．

一、分析:理清思路,探究前的解题思路论证

这是一道解析几何题,按照数学的发展史看,需要用代数方法来解决几何问题.但从本质上讲它仍然是几何问题,几何图形所具有的特性仍然存在,它从未失去几何的本性．因此,笔者认为对于解析几何的问题通常可以按照两大方向进行．其一,由代数方法出发,利用题目中存在的数量关系建立代数关系式,通过代数方法求解.其二,由题目的几何性质出发,通过几何性质建立关系求解．

声音1:这种观点并不是绝对的,解析几何的方法就是从用代数方法来解决几何问题,这也正是笛卡尔和费马建立解析几何的原始意义,且并不是所有的解析几何问题都能利用几何性质解决．

声音2:解析几何仍然存在图形,有图形就会存在有关的几何性质,有几何性质就可以利用性质来解题．只不过有些题目的几何性质易发掘,而有些题目难以挖掘出几何性质而已．

声音3:比较两种思路,可以发现各自的优劣之处:代数法在思维的流畅性上要优于几何法,然而,它根植于计算的特性会让整体的计算量较大.与之相反,几何法计算量较小,但在思维的复杂程度上要更胜代数思维．因此,在利用几何性质解决时,易使学生陷入思维的困境．

二、探究:各自求解,凭一已之力的解题摸索

带着先前讨论的的解题思路,各人独自对这题进行了探究.笔者的解题摸索过程如下:

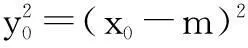
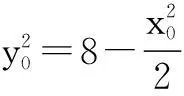
∵PP′⊥x轴,

∴圆与椭圆的交点横坐标只有一解,即

Δ=0，

∴Δ=16m2-12(2m2-16)=0,

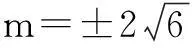
三、寻错:集思广益,集众人之力寻错误根源

在下述交流的过程中,经过众人的讨论,重新理顺思路,逐步明晰了错误的根源．

声音1:在上述解题过程中,关于圆和椭圆的位置关系如何得到体现呢?

声音2:在上述求解过程中,如何体现使椭圆上的其余点均在圆Q外?

笔者:点P、P′在圆上,PP′⊥x轴,说明点P、P′横坐标相同,即圆与椭圆的交点的横坐标只有一个,即所化成关于x0的方程只有一解,等价于Δ=0．

经过个人和同事对计算过程的反复检查,发现整个计算的过程并不存在计算错误.既然计算不存在错误,就意味着解题的依据出现了问题．与同事讨论,发现彼此的解题依据是利用了圆与椭圆的交点横坐标只有1解,故而构造了一个关于点P横坐标的一元二次方程,利用Δ=0来求解参数m的值．这样的解释似乎不存在问题,那问题究竟出在何处呢?这让大家再次陷入了深思．

声音3:再次审视上面的解题过程尤其是你的解题的纽带,你会发现这样的问题对于

是通过

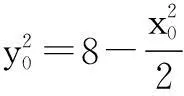
四、再探:疑问再现,解疑中提升思维完整性

发现错误后,重新对思路进行了梳理,要建立圆与椭圆的联系,选用代数方法建立联系,求什么设什么.

设Q(m,0),⊙O:(x-m)2+y2=r2．

①

由Δ=4m2-2(m2-r2+8)=0，得

r2=8-m2.

②

将② 式代入①式，可得

解得x=2m，P(2m,y),P′(2m,-y)，

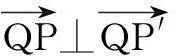
∴m2-y2=0,

解得y=m,∴P(2m,m).

点P在椭圆上,满足椭圆方程

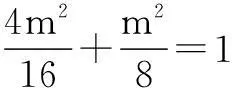
故圆的方程为

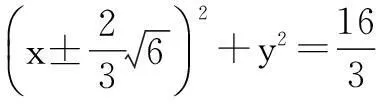
声音1:你的解题依据是圆与椭圆的交点的横坐标只有一个,构造了一个关于点P横坐标的一元二次方程,利用Δ=0来求解参数m的值．请你分析下面这种情况是否也满足你的解题依据?

比较题目给出的图形和设想的图形(图2)可以发现,两者均满足圆与椭圆交点的横坐标只有一个,因此你的解题依据存在问题．

同事的问题让我再次陷入了深思.毫无疑问,上述的解是符合题意的,说明从代数的角度入手的解题过程不错,但同事的问题也为上述过程画出了问号.那么上述解题过程能否作为解题过程呢?我们又开始了新一波的讨论．

声音2:Δ=0可以作为解题的依据,从命题的关系看,两幅图可以推出Δ=0,但Δ=0推不出唯一的图.因此，Δ=0是题目所给图形表示命题的必要条件,即由题意一定可以得出Δ=0,但为加强解题的严谨性,在解题后要对解得数值进行检验．

通过同事之间的讨论终于从代数的角度给这道问题一个思维完整的解答.从这个讨论过程中暴露出了个人思维的缺陷,同时也体现了集体智慧的伟大．当然这还不是整个讨论的全部,文章开始从几何角度未能取得突破,在继续的讨论过程中也有了新的进展．

声音3:细读题目,“椭圆上其它的点均在圆外”这句隐藏了一个非常重要的几何性质,即圆外的点到圆心的距离大于半径(PQ),因此,点P是椭圆上到点Q距离最小的点．

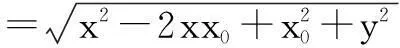
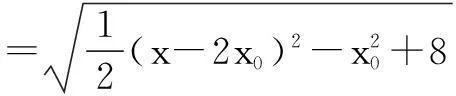
x∈[-4,4].

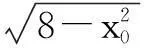
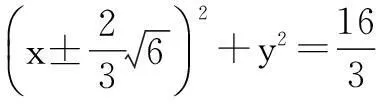
五、感悟：交流激荡思维,讨论促进发展

上述讨论过程以一道解析几何为例,从思想方法的探讨开始,经个人摸索,寻找错误,完善思维等过程.这一讨论不仅解决了题目,提升个人思维的完整性,激荡了教师群体的思维,也验证相关的思想理论方法．尽管上述讨论过程仅仅教师探讨话题的一个缩影,但却反映了教师之间的交流对教师、学生和教学的重要意义．首先,个人的精力是有限的,群体的智慧是无穷的,教师间的交流就是一个激荡群体思维,展现群体智慧的过程．交流活动可以充分利用学校教学资源,创建一个教研的气氛,增进教师之间的感情,推广好的教学经验,从而最大限度地促进教师成长．其次,师者,传道、授业、解惑也，学生的成长以教师的引领为前提,老师良好的引领作用以扎实的专业素养为基础,交流促进老师良好的成长,必然会引领学生良好的发展．最后,教师的交流的过程,本身就是填补教学过程的重要素材,好的老师可以从交流过程汲取养分,合理规划整个教学过程,使课堂变得丰满,使教学变得有血有肉．