函数y=Asin(ωx+φ)解析式的教学实践与思考
2016-07-08居加颖
居加颖
(江苏省南京市宁海中学,225605)
函数y=Asin(ωx+φ)解析式的教学实践与思考
居加颖
(江苏省南京市宁海中学,225605)
一、教学背景
本节课是在我校的青年教师赛课中开设的,所教班级为高一(12)班——美术班,学生的数学基础相对文化班略显薄弱,在教学过程中,主要注重以基础知识为主,能力提升为辅.
二、教材分析
本节课的教学目标:(1)根据正弦函数的变换得到函数y=Asin(ωx+φ)的解析式;(2)能够根据图象所给信息,求出函数y=Asin(ωx+φ)的解析式;(3)进一步体会数形结合方法.
教学重点:根据图象求出函数y=Asin(ωx+φ)解析式.
教学难点:分别根据具体图象信息求出参量A,ω,φ的值.
三、教法分析
学生在学习数学的过程中,一方面需要老师的指引;另一方面需要自己的探索发现.所以本节课,笔者采用启发引导式教学.
四、教学过程
1.问题情境
提问:上一节课,我们学习了什么知识?
设计意图让学生回顾上一节课所学知识,为本节课做好知识衔接.
反思学生开始不知道如何说出所学知识,因为问题设置过大,复习提问要应先复习框架,然后分支展开回顾,这样,学生能够清晰回顾所学知识.
2. 学生活动
(1)引导学生用“五点法”画函数y=Asin(ωx+φ)的图象,理解A,ω,φ的物理意义.
(2)掌握函数y=Asin(ωx+φ)与y=sinx图象间的变换关系.
设计意图引领学生理清思路,知道A,ω,φ的意义,以及明白函数y=Asin(ωx+φ)的图象如何由y=sinx图象变换而得.
3.建构数学与数学运用
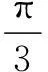


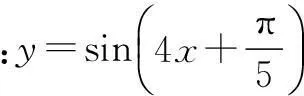
注意点横向平移与横向伸缩,仅对x作变换.
设计意图上一节课,给定解析式,学生知道如何由正弦函数平移而得,本节课学生需要自己根据给定变换,得到变换后的解析式,例1是基础题,变式增加了“陷阱”,考察学生是否真正理解变换的本质.
反思例1学生做得比较顺利,在变式的解题过程中,有两个“陷阱”,学生只要抓住平移变换只针对x即可.
答案:2.
注意点求ω时要善于捕捉图象中给定的周期信息.
变式函数y=Asin(ωx+φ)(A>0,ω>0)在闭区间[-π,0]上的图象如图2所示,则ω=______.
答案:3.
设计意图例2旨在让学生体会到,要求ω,关键是要捕捉图象中关于周期的信息.
反思变式在设计上欠妥,有两种调整方式:一是只给出-π一个点的坐标,其他两个坐标不给出,让学生自己寻找,增加做题的乐趣;二是为了例3的变式1做准备,给出一个不含π的周期,让学生提前感受一下周期没有π的情形时,ω的取值与周期有π时的区别.

评注求φ要找关键点,一般找图象中最高点或最低点,并且,要注意题目给定的范围;求A要根据图象的最值.
变式1图4所示图形是y=Asin(ωx+φ)(ω>0,|φ|<π)的图象的一段,试确定其解析式.
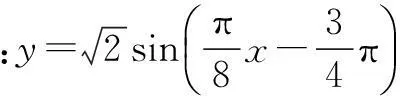
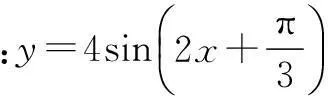
设计意图例3需要学生分别求出三个参量,难度提升,但对于A,ω的求解并没有困难,关键是如何求出φ,提醒学生图象中还有信息可以利用,就是最高点、最低点.变式1的设计基于两点:一是A的值不是1,要根据最大值得到;二是若求φ时代入(-2,0)或(6,0),学生会得到两个答案,而感到困惑.此时指引学生找出两个答案的原因,并探索,怎样才能得到一个正确答案.
反思教学过程中直接给出例3,让学生去求解析式,有些唐突.学生做题不规范,也有学生无从下手,在一节课中,应该要有一个主打的例题.在本节课中,例3应该作为主打题目,带着学生一起完成,让学生理解求解析式的具体步骤.变式1中,周期没有π,学生感到比较奇怪,所以在前面的周期的求解中应该增加一个类似的题目,让学生提前感受周期没有π的情况.变式2的主要目的是在没有图的情况下,学生要自己去画图,将文字语言转化为图形语言,再从图形语言转化为数学语言,这个对能力的要求比较高.在实际教学中,没有充分的时间让学生去思考,在设计中应该省去或调整为简单的题目.
4.方法小结
求函数的解析式的途径有两种:一是通过变换得到;二是根据图象来求(由周期求ω,由最值求A,由特殊点求φ).
5.作业布置(略)
五、教学反思
本节课,课堂气氛活跃,学生能够全程认真参与,在回答问题、解答题目时都深入思考,作为美术班的学生,这是难能可贵的.在教学中,教师应充分调动学生的积极性,引导学生在课堂上主动参与,积极思考,将所学知识灵活运用.但在教学过程中,遇到学生的回答没有令老师满意时,不能着急去打断,而应该鼓励学生继续往下说,尽量引导学生得到正确答案.在学生求解析式中的参量时,不能提前强调注意点,应该等着学生出现问题,感到束手无策时,再带着学生分析问题,并找到最好的解法.这样,学生感觉是自己发现错误并纠正的错误,他们能加强记忆,并油然而生一种自豪感,增加学习数学的兴趣.
