基于三角模糊数和AHP的海洋平台风险评价方法

姜　峰,曹　康,杨旭兵

(兰州理工大学 石油化工学院,甘肃 兰州　730050)



基于三角模糊数和AHP的海洋平台风险评价方法

姜峰,曹康,杨旭兵

(兰州理工大学 石油化工学院,甘肃 兰州730050)

摘要采用三角模糊数和AHP综合的评价方法对海洋平台风险进行评估。首先简述了三角模糊数理论和运用AHP方法确定权重的步骤,并建立了基于三角模糊数和AHP的综合评价模型。然后以渤海某海洋平台为实例,建立了风险评价指标体系,采用AHP法确定了各因素权重。最后进行了三角模糊综合评价,结果为GB=2.815,确定了风险等级为“一般”,并针对评价结果提出了相应的预防管理措施,从而验证了该方法的可行性。

关键词三角模糊数;AHP;海洋平台;风险评价

随着海洋经济时代的到来,人类在海洋上的作业越来越多,随之而来的灾难性事故也不断发生。这些灾难的发生,不但使很多人死于非命,而且造成了巨大的经济损失和严重的环境污染[1]。目前,挪威、英国等海上石油强国已经拥有了比较完善的海洋石油平台风险评价体系。我国海上石油工业起步较晚,但随着渤海二号翻沉(72人死亡),Jeve Sea钻井船在莺歌海的倾覆(81人死亡),珠江口惠州铺管船翻沉(22人死亡),以及其他海难事故的不断发生,海洋平台风险评价越来越受到人们的重视[2]。

如今,早期所建海洋平台逐渐趋于结构老化,因此海洋平台领域的安全评估被提上议程,一些新的评估方法也得到了发展和应用。近年来,英国在海洋平台的安全评估方面发展较快,方法也比较完善和先进。与国外相比,国内在该方面的研究尚有较大的差距[3]。由于海洋平台风险的评价往往不是以精确的数字出现,其评价边界具有一定的模糊性,而采用模糊综合比较的方法能够将模糊的评价转为精确的数字比较,故这一方法在海洋石油工程风险评估中得到了广泛运用。但是,一般的模糊综合评价法在量化过程中选择的是平均数,会造成许多有用信息丢失,最终可能导致评价结果不符合实际情况。此外,海洋平台风险因素具有复杂性和多层次性,评判中各因素权重分配往往不太合理。为了弥补这两大缺陷,研究提出采用基于三角模糊数和AHP的综合评价模型对海洋平台风险进行评估。

1AHP和三角模糊数的综合评价模型

1.1AHP方法步骤

美国运筹学家Saaty于20世纪70年代提出了层次分析法(AHP,analytic hierarchy process)。这是一种定量和定性相结合的决策方法,它把复杂的问题分解成各个组成因素,通过两两比较的方式确定层次中诸因素的相对重要性,然后通过综合判断决定诸因素相对重要性的总顺序。运用AHP方法计算权重大体分为以下几个步骤[4-8]：

(1)采用“1～9标度法”表示因素间的相对重要程度,构造判断矩阵。标度及含义如表1所列。

(2)计算n阶判断矩阵的最大特征值λmax和特征向量A=(a1,a2,…,as),并判断随机一致性指标C.R,其中：

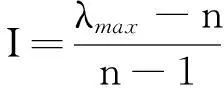
(1)

(2)

一致性指标R.I可通过查表得到[6]。

当C.R<0.1时,认为判断矩阵一致性良好,说明权重分配合理,用最大特征值λmax对应的特征向量A=(a1,a2,…,as)作为权重向量w=(w1,w2,…,wn);否则需要调整判断矩阵,直到具有良好的一致性为止。

1.2三角模糊数

若模糊数A可由(a,b,c)决定,且隶属函数值为[9]

则称A为三角模糊数,记为A=(a,b,c),当a=b=c时,A为一个精确数。三角模糊数的分布如图1所示。

1.3三角模糊数综合评价

三角模糊数综合评价分为以下几个步骤[9-13]：

(1)确定指标体系权重

在模糊综合评判中,因素权重集的确定是否恰当直接影响综合评价的结果。为了减少主观因素的影响,采用AHP确定因素权重,记为

W=[w1w2… wn]。

(2)建立三角模糊数矩阵

设有n个评价指标,有p个专家参与评价决策,对于第j个指标,第i个专家给出的评价结果为[aij,bij,cij],其中:aij表示第i个专家对第j个指标给出的最保守的评价;bij表示第i个专家对第j个指标给出的最可能的评价;cij表示第i个专家对第j个指标给出的最乐观的评价。由p个专家对n个评价指标进行打分,从而形成了基于三角模糊数的初始综合评判矩阵：

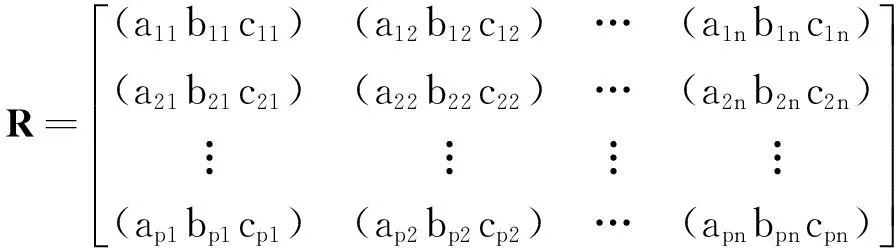
(3)集合专家打分

首先确定参加评价打分专家的权重,记为

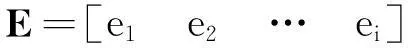
其中:ei表示第i个专家给出的评价打分在综合评价中所占的比重。

然后根据下式集合各位专家的评价打分：

(3)

其中:(aibici)为第i个指标的模糊综合评价值;ai为对第i个指标的最保守评价;bi为对第i个指标的最可能评价;ci为对第i个指标的最乐观评价;显然有ai≤bi≤ci。

(4)综合评价

首先根据下式将各个指标的模糊综合评价结果进行综合：

(abc),

(4)

其中:(abc)为安全评价的模糊综合评价结果。

再根据三角模糊数的分布特点,运用公式[11]

(5)

将三角模糊数(abc)化为单值,即可得到最终评价结果。

2实例应用

以渤海某导管架采油平台为例进行三角模糊综合评价。此平台1998年建成投产,设计服役年限30年。首先通过调查研究建立风险评价指标体系,并采用AHP法确定各指标权重。然后请四位专家打分,建立三角模糊数矩阵。最后集合专家打分,进行单模块评价和综合评价,并与现场专家判断结果比较。

(1)建立评价指标体系

通过对国内外海洋平台事故资料的统计分析并结合众多学者的研究[14-17],发现人员、平台、管理、环境四大因素是引起海洋平台事故的主要诱因。鉴于此,我们将这四大类作为评价模型的一级指标,并选取其中11个主要风险因素作为二级指标,最终确定的风险评价指标体系如表2所列。

(2) 确定指标权重

请业内专家和现场安全管理人员对表2中所列指标进行两两比较打分,构造判断矩阵,再根据1.2所述AHP 法及式(1)、式(2)确定各层次指标的权重,具体数据和结果见表3。

(3)建立三角模糊数矩阵

以人员因素B1模块为例,请四位行业专家按照表4所述的“1～5分”评分等级和三角模糊数的定义,根据该海洋平台安全管理工作的实际情况对B1模块中的指标进行评价打分,建立三角模糊数矩阵：

(4)集合专家打分

首先根据专家们的工作背景与经验,将参加评价打分的四位专家的权重确定为

E=[e1e2e3e4]=[0.20.30.30.2]。

然后根据式(3)集合各位专家的评价打分:

(5)进行综合评价

首先根据式(4)将人员因素B1模块中各个指标的模糊评价结果进行综合：

再根据式(5)对评价结果进行单值化处理,可得

由3.23∈[3,4)可知,人员因素B1模块的综合评价结果为“较安全”。

同理,通过上述过程可以将其他三个模块中各个指标的模糊评价结果进行综合：

TB2= [1.87,2.16,2.44],

TB3= [3.79,4.12,4.41],

TB4= [2.58,2.96,3.23]。

这三个模块的最终评价结果分别为

平台因素B2模块GB2= 2.16∈[2,3),即“一般”;

管理因素B3模块GB3= 4.11∈[4,5),即“安全”;

环境因素B4模块GB4= 2.94∈[2,3),即“一般”。

通过式(4)可得该海洋平台安全评价的总模糊综合评价结果为

利用公式可得该海洋平台安全评价的最终结果为

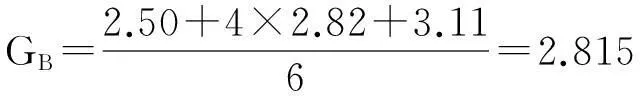
通过最终的总评价结果可知2.815∈[2,3),即该海洋平台安全状况为“一般”。这一结果与现场专家判断一致。

此外,由每个模块评价结果可知,平台因素和环境因素安全状况等级为“一般”,是该海洋平台的主要风险因素,应该加强这两方面的安全管理。

3结论

(1)利用AHP法确定海洋平台风险因素权重,充分减少了主观因素对权重的影响,有效地解决了权重分配困难的问题,使得权重更加客观合理,评价结果更加符合实际情况。

(2)采用的三角模糊数综合评价充分考虑了专家主观评价、判断的模糊性,扩大了可利用信息的范围,使最终的计算结果更贴近实际。同时,又利用三角模糊数分布特点,采用其平均值大小来比较模糊三角数大小,将模糊比较转化为精确数的比较,既简化了计算步骤,又扩大了有效信息量,在多指标安全评价问题上为决策者提供了一种更加简便、实用的方法。

(3)以渤海某海洋平台为例对该评价模型进行了实证分析,最终评价结果为GB=2.815,得到该海洋平台的整体安全状况为“一般”。此外,根据各个模块的评价结果得出平台因素和环境因素安全状况等级为“一般”,是该海洋平台的主要风险因素,为管理工作者及时掌握海洋平台安全管理状况、采取有效措施提升安全管理水平提供了依据。

参考文献：

[1]李玉刚,林焰,纪卓尚.海洋平台安全评估的发展历史和现状[J].中国海洋平台,2003,18(1):4-8.

[2]李奇,牟善军,姜巍巍,等.海上石油平台定量风险评估[J].中国海洋平台,2007,22(6):38-42.

[3]陶冉冉,闫相祯,刘锦坤.浅谈安全评估在海洋平台上的应用[J].石油和化工设备,2010,13(2):46-47,56.

[4]邓雪,李家铭,曾浩健,等.层次分析法权重计算方法分析及其应用研究[J].数学的实践与认识,2012,42(7):93-100.

[5]任玉辉,肖羽堂.层次分析法在校园火灾危险性分析中的应用[J].安全与环境工程,2008,15(1):85-88.

[6]汪应洛.系统工程[M].第2版.北京:机械工业出版社,2003.

[7]杨仲玮.基于模糊评价法的山丹河水质评价研究[J].甘肃科学学报,2014,26(6):68-71.

[8]张贵文,张海梅.基于模糊理论的钢筋混凝土结构耐久性评价[J].甘肃科学学报,2013,25(3):76-79.

[9]胡永宏,贺思辉.综合评价方法[M].北京:科学出版社,2000.

[10]张元,李敬.基于三角模糊数的民航企业“管理”安全综合评价模型研究[J].中国安全科学学报,2008,18(9):141-146.

[11]廖勇.基于三角模糊数的铁路客运站选址方案评价方法[J].中国铁道科学,2009,30(6):119-125.

[12]龚玉霞,吴育华.ATM机选址的三角模糊数综合评价方法[J].工业工程,2005,8(6):104-107.

[13]肖钰,李华.基于三角模糊数的判断矩阵的改进及其应用[J].模糊系统与数学,2003,17(2):59-64.

[14]于海洋.海上移动式平台综合安全评价的研究[D].大连:大连海事大学,2008.

[15]姜蕊.老龄海洋石油平台风险评估研究[D].大庆:大庆石油学院,2010.

[16]肖建勇.海洋平台安全风险分析方法研究[D].天津:天津大学,2003.

[17]庄力健,陈学东,陈炜,等.在役海洋石油平台风险分析与安全运行关键技术探讨[J].压力容器,2014,31(6):51-57.

Risk Evaluation Method of Ocean Platform Based on Triangular Fuzzy Number and AHP

Jiang Feng,Cao Kang,Yang Xubing

(College of Petrochemical Engineering,Lanzhou University of Technology,Lanzhou 730050,China)

Key wordsTriangular fuzzy number;AHP;Ocean platform;Risk evaluation

AbstractRisk evaluation on ocean platform based on a comprehensive evaluation methodology of triangular fuzzy number and AHP(analytic hierarchy process) is proposed.First,theory of triangular fuzzy number and steps of applying AHP to determine weight are briefly introduced,and comprehensive evaluation model based on triangular fuzzy number and AHP is built.Then,risk evaluation index system is built by taking one ocean platform of Bohai Sea as living example,and weight of each factors id determined by adopting AHP.At last,a comprehensive evaluation of triangular fuzzy number is conducted.The results show that GB=2.815.The risk grade is determined as "general".Relevant measures of prevention and management are proposed against evaluation results,which verify the viability of this method.

doi:10.16468/j.cnki.issn1004-0366.2016.03.014.

收稿日期：2015-04-07;修回日期：2015-05-14.

基金项目:国家质检公益项目(201310152):基于风险管理的油气集输压力容器安全评定关键技术研究.

作者简介:姜峰(1969-),女,湖南宁乡人,硕士,教授,硕士生导师,研究方向为承压设备.E-mail:921238461@qq.com.

中图分类号:P751

文献标志码：A

文章编号：1004-0366(2016)03-0067-05

引用格式:Jiang Feng,Cao Kang,Yang Xubing.Risk Evaluation Method of Ocean Platform Based on Triangular Fuzzy Number and AHP[J].Journal of Gansu Sciences,2016,28(3):67-71.[姜峰,曹康,杨旭兵.基于三角模糊数和AHP的海洋平台风险评价方法[J].甘肃科学学报,2016,28(3):67-71.]