一类紧支撑正交多小波的显式构造

张建基,雷巧莉,关惠惠,张　静

(1.新疆师范大学 数学科学学院,新疆 乌鲁木齐　830054;2.西安铁路职业技术学院,陕西 西安　710014)



一类紧支撑正交多小波的显式构造

张建基1,雷巧莉2,关惠惠1,张静1

(1.新疆师范大学 数学科学学院,新疆 乌鲁木齐830054;2.西安铁路职业技术学院,陕西 西安710014)

摘要以所构造的正定矩阵为基础,给出了2尺度紧支撑正交多小波的构造方法,证明了当2尺度r重紧支撑正交多尺度函数的系数矩阵Pi是r×r阶可逆矩阵,存在正交矩阵A,使与diag(λi,1,λi,2,…,λi,r)合同。算例的结果说明,当-1PiPiTA是对角的正定矩阵时,可构造出2重紧支撑正交多小波函数。

关键词紧支撑正交多小波;对称正定矩阵;对角矩阵

多小波的理论和应用研究已经引起了广泛的关注[1-4],目前多小波的构造方法有:一是仿酉矩阵的扩充,而矩阵扩充过程相当复杂;二是在文献[5-8]中所应用的构造多小波的方法。

1预备知识

设Φ(x)=[φ1(x),φ2(x),…,φr(x)]T是一个具有r重紧支撑正交多尺度函数向量。有

Vj=closL2(R)〈φi(2jx-k)∶1≤i≤r,k∈Z〉,j∈Z

(1)…⊂Vj-1⊂Vj⊂Vj+1⊂…,∀j∈Z;

(3)f(x)∈Vj⟺f(2x)∈Vj+1,j∈Z；

(4)函数族{Φ(·-k):k∈Z}构成V0的一个Re siz基,则称此多重多分辨分析有Φ(x)生成。

多尺度函数向量Φ(x)的两尺度方程为

(1)

设Wj是Vj在Vj+1中的正交补,即Vj+1=Wj⊕Vj。若Ψ(x)=[ψ1(x),ψ2(x),…,ψr(x)]T的平移{Φ(·-k):k∈Z}构成W0的正交基,则称Ψ(x)为对应于正交多尺度函数Φ(x)的正交多小波。有

(2)

对式(1)、式(2)做Fourier变换,有

(3)

(4)

若Φ(x)与Ψ(x)为正交函数向量,则有

P(ω)P*(ω)+P(ω+π)P*(ω+π)=Ir×r,

(5)

P(ω)Q*(ω)+P(ω+π)Q*(ω+π)=Or×r,

(5)

Q(ω)Q*(ω)+Q(ω+π)Q*(ω+π)=Ir×r,

(7)

可等价于

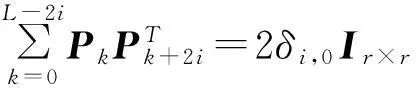
(8)

(9)

(10)

22尺度r重紧支撑正交多小波

证明Pi是可逆矩阵,则存在正交矩阵A和B有

ATPiB=diag(σi,1,σi,2,…,σi,r)。

则有

由于B是正交矩阵,所以有

diag(λi,1,λi,2,…,λi,r)。

证毕。

则

证毕。

对角矩阵在求逆时计算量很少,只需将对角线上的元素取倒数,并且对角矩阵与对角矩阵在相乘时可以交换,基于对角矩阵的这两个良好性质,我们将在引理2中给出如何构造出对角的正定矩阵。

是对角的正定矩阵。

证明由引理1知,存在正交矩阵A,有

(11)

又有

(12)

(13)

证毕。

推论2若2尺度r重紧支撑多尺度函数Φ(x)的系数矩阵P0,P1,…,PL中Pm和Pn(0≤m,n≤L)是可逆矩阵,A是正交矩阵且

其中:0<λj<2(0≤j≤r),则

是对角的正定矩阵。

定理1设Φ(x)是二系数的2尺度r重紧支撑正交多尺度函数,满足两尺度方程

Φ(x)=P0Φ(2x)+P1Φ(2x),

其中:P0,P1是r×r阶矩阵,选取可逆矩阵Pi(0≤i≤1),存在正交矩阵A有

令

(14)

则可构造

(15)

其中:K-1表示K的逆矩阵,则ψ(x)加细方程

Ψ(x)=Q0Ψ(2x)+Q1Ψ(2x)

(16)

是对应于Φ(x)的2尺度r重紧支撑正交的多小波函数。

证明只要满足下列的等式,原命题就成立,即

P0(Q2)T=0,

(17)

P2(Q0)T=0,

(18)

Q0(Q2)T=0,

(19)

P0(Q0)T+P1(Q1)T+P2(Q2)T=0,

(20)

Q0(Q0)T+Q1(Q1)T+Q2(Q2)T=2I。

(21)

由于Φ(x)是二系数的2尺度r重紧支撑正交多尺度函数,所以P2=0且Q2=0,则有P0P2=0和P2P0=0。式(17)～式(19)的证法相似,只需证明式(19),设i=0,即选取的是P0,有

Q0(Q2)T=-K-1ATP0(0)T=0,

Q0(Q0)T+Q1(Q1)T=(-K-1ATP0)(-K-1ATP0)T+KATP1(KATP1)T=

证毕。

定理2设Φ(x)是三系数的2尺度r重紧支撑正交多尺度函数,满足两尺度方程

Φ(x)=P0Φ(2x)+P1Φ(2x)+P2Φ(2x),

其中:P0,P1,P2是r×r阶矩阵,选取其中一个可逆矩阵Pi,存在正交矩阵A有

令

(22)

则可构造

Qj=KATPj,j≠i,j=0,1,2

Qj=-K-1ATPj,j=i,j=0,1,2

(23)

其中:K-1表示K的逆矩阵,则ψ(x)加细方程

Ψ(x)=Q0Ψ(2x)+Q1Ψ(2x)+Q2Ψ(2x)

(14)

是对应于Φ(x)的2尺度r重紧支撑正交多小波函数。

证明只要满足下列的等式,原命题就成立,即

P0(Q2)T=0,

(25)

P2(Q0)T=0,

(26)

Q0(Q2)T=0,

(27)

P0(Q0)T+P1(Q1)T+P2(Q2)T=0,

(28)

Q0(Q0)T+Q1(Q1)T+Q2(Q2)T=2I。

(29)

由于Φ(x)是2尺度r重紧支撑正交多尺度函数,有P0P2=0和P2P0=0。式(25)～式(27)的证法相似,只需证明式(27)。设i=0,即

Q0(Q2)T=-K-1ATP0(KATP2)T=

式(18)、式(19)的证法同定理1中式(20)、式(21)的证明方法。

证毕。

定理3设Φ(x)是四系数的2尺度r重紧支撑正交多尺度函数,满足两尺度方程

Φ(x)=P0Φ(2x)+P1Φ(2x)+P2Φ(2x)+P3Φ(2x),其中:P0,P1,P2,P3是r×r阶矩阵,选取可逆矩阵P0和P1,存在正交矩阵A有

(30)

则可构造

(31)

其中:K-1表示K的逆矩阵,则Ψ(x)加细方程

Ψ(x)=Q0Ψ(2x)+Q1Ψ(2x)+

Q2Ψ(2x)+Q3Ψ(2x)

(32)

是对应于Φ(x)的2尺度r重紧支撑正交多小波函数。

证明只要满足下列的等式,原命题就成立,即

P0(Q2)T+P1(Q3)T=0,

(33)

P2(Q0)T+P3(Q1)T=0,

(34)

Q0(Q2)T+Q1(Q3)T=0,

(35)

P0(Q0)T+P1(Q1)T+P2(Q2)*+P3(Q3)T=0,

(36)

Q0(Q0)T+Q1(Q1)T+Q2(Q2)*+Q3(Q3)T=2I。

(37)

Q0(Q2)T+Q1(Q3)T=-K-1ATP0(KATP2)T-

K-1ATP1(KATP3)T=

式(36)和式(37)的证法同定理1中式(20)和式(21)的证明方法。

证毕。

注定理3中K2除了可以选取P0和P1,还能选取P2和P3,有两种选取方法。

3算例

例1Φ(x)是二系数的2尺度2重紧支撑正交多尺度函数,满足两尺度方程

Φ(x)=P0Φ(2x)+P1Φ(2x),

第二步计算K得

第三步由

则

例2Φ(x)是三系数的2尺度2重紧支撑正交多尺度函数,满足两尺度方程

Φ(x)=P0Φ(2x)+P1Φ(2x)+P2Φ(2x),

其中:

可知P1是可逆的矩阵,则用定理2。

第二步计算K得

则

第三步由

则

参考文献:

[1]Donovan G C,Geronimo J,Hardin D P.Construction of Orthogonal Wavelets Using Fractal Interpolation Functions[J].SIAM J.Math.Anal,1996,27:1 158-1 192.

[2]Li Youfa,Yang Shouzhi,Yuan Dehui.Bessel Multiwavelet Sequences and Dual Multiframelets in Sobelev Spaces[J].Adv Comput Math,2013,38:491-529.

[3]Li Youfa,Yang Shouzhi.A Class of Multiwavelets and Projected Frames from Two-direction Wavelets[J].Acta Mathematical Scientia,2014,34:285-300.

[4]Yang Shouzhi.Biorthogonal Interpolatory Multiscaling Functions and Corresponding Multiwavelets,The ANZIAM Journal,2007,49:85-97.

[5]Chui C K,Lian J.A Study on Orthogonal Multiwavelets[J].Appl.Numer.Math.,1996,20:273-298.[6]Yang Shouzhi,Tang Yuanyan,Cheng Zhengxing.Construction of Compactly Supported Orthogonal Multiwavelet with Scale=a[J].Mathematica Numberica Sinica,2002,24:451-460.

[7]Chen Qingjiang,Cheng Zhengxing.A Study on Compactly Supported Orthogonal Vector-valued Wavelets and Wavelet Packets[J].Chaos,Solitons and Fractals,2007,31:1 024-1 034.[8]Cen Yigang,Cen Lihui.Explicit Construction of High-pass Filter Sequence for Orthogonal Multiwavelets[J].Applied Mathematics and Computation,2009,213:235-242.[9]Kessler B.A Construction of Compactly-Supported Biorthogonal Scaling Vectors and Multiwa-Velets on R2[J].J Approx Theory,2002,117:229-254.

[10]徐建设,金坚明.样条小波有限元法[J].甘肃科学学报,2001,13(4):10-14.

[11]Kessler B.A Construction of Orthogonal Compactly Supported Multiwavelets on R2[J].Appl Comput Harmon Annal,2000,9:146-165.

[12]金坚明.多维样条小波变换[J].甘肃科学学报,1998,10(3):1-6.

Explicit Construction of First Class Compact Supported Orthogonal Multi Wavelets

Zhang Jianji1,Lei Qiaoli2,Guan Huihui1,Zhang Jing1

(1.School of Mathematical Science,Xinjiang Normal University,Urumqi 830054,China;2.Xi’an Railway Vocational & Technical Institute,Xi’an 710014,China)

Key wordsCompact supported orthogonal multi wavelets;Symmetric positive definite matrix;Diagonal matrix

AbstractBased on the constructed positive definite matrix,construction method of compact supported orthogonal multi wavelets with dilation factor 3 are presented to prove that coefficient matrix of compact supported orthogonal multi-scaling functions with dilation factor 2 is an invertible matrix with order,and orthogonal matrix exists in making same with.The result of example indicates that 2 compact supported orthogonal multi-wavelet function can be constructed when is diagonal positive definite matrix.

doi:10.16468/j.cnki.issn1004-0366.2016.03.005.

收稿日期:2015-03-10;修回日期:2015-11-27.

作者简介:张建基(1989-),男,甘肃武威人,硕士研究生,研究方向为小波分析及其应用.E-mail:1454920447@qq.com.

中图分类号:O174.2

文献标志码:A

文章编号:1004-0366(2016)03-0020-06

引用格式:Zhang Jianji,Lei Qiaoli,Guan Huihui,et al.Explicit Construction of First Class Compact Supported Orthogonal Multi Wavelets[J].Journal of Gansu Sciences,2016,28(3):20-25.[张建基,雷巧莉,关惠惠,等.一类紧支撑正交多小波的显式构造[J].甘肃科学学报,2016,28(3):20-25.]