湍流对截断光束瑞利区间的影响
2016-07-07王宇峰陈晓文汤明玥
王宇峰,陈晓文,汤明玥
(川北医学院 a.医学影像学院;b.基础医学院物理教研室,四川 南充 637000)
湍流对截断光束瑞利区间的影响
王宇峰a,陈晓文a,汤明玥b
(川北医学院a.医学影像学院;b.基础医学院物理教研室,四川 南充 637000)
摘要:推导出截断光束在自由空间和湍流中的瑞利区间表达式,并研究了光束参数和湍流强度对瑞利区间的影响。研究发现,湍流中瑞利区间随湍流强度的增大而逐渐减小。另一方面,不论在自由空间还是湍流中,瑞利区间都随相干参数β和δ截断参数的增大而增大。β和δ取较小值时,湍流对瑞利区间的影响可以忽略不计;而随β和δ的增大,湍流对瑞利区间的影响逐渐增大。
关键词:截断光束;瑞利区间;湍流;截断参数
长期以来,激光在光通信、检测、遥感等方面的应用备受科研工作者的关注,因此研究激光束在大气中的传输有着重要的意义[1]。大气环境极为复杂,选取一个更为贴近实际情况的理论模型显得尤为重要。近期,非Kolmogorov湍流模型得到了普遍认可并被广泛应用[2]。文献[3-5]研究了各类激光束在非Kolmogorov湍流中的传输特性。
另一方面,在激光理论中,瑞利区间指光束无明显扩展时的传输距离[6],是描述光束扩展情况的物理参量。2009年,季小玲等研究了完全相干和部分相干列阵光束的瑞利区间,并发现列阵光束的瑞利区间随子光束数目的增加而增加[7]。
截断光束是普遍存在的一类激光束(由激光器所产生的激光常会受到光阑的限制,即产生截断光束),然而对于截断光束在湍流中传输的扩展研究甚少[8-9]。本文给出了截断光束在自由空间和湍流中的瑞利区间表达式,并论述了光束参数和湍流参数对其的影响。
1理论推导
截断光束是激光束通过硬边光阑后产生的光束,在实际激光束中普遍存在。假设某圆形硬边光阑半径为d,则其窗口函数可表示为[9]

(1)
H(x)亦可展开为复高斯函数的有限级数和[9]

(2)
式(2)中展开系数Fi、高斯系数Gi及M具体数据参见文献[10]。
假定通过硬边光阑前的激光束为高斯—谢尔光束(GSM光束),GSM光束在源场(z=0)处的交叉谱密度函数表示为[11]
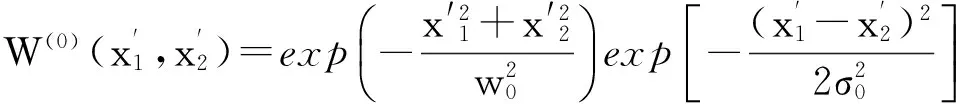
(3)
其中,w0和σ0分别为光束在源场处的束腰和空间相干长度[11]。
因此,依据广义惠更斯—菲涅尔原理,截断光束通过自由空间传输时在远场(z>0)处光强表示为[11]
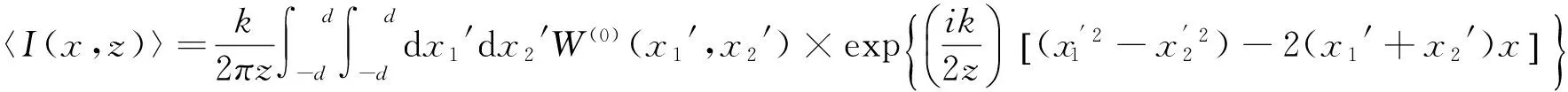
(4)
其中,波数k与波长λ有关(k=2π/λ)。
二阶矩束宽可定义为[12]

(5)
采用积分变换技术,通过复杂的积分运算可得到截断光束在自由空间中传输的二阶矩束宽
w2(z)=A+B·z2,
(6)
其中

(7)
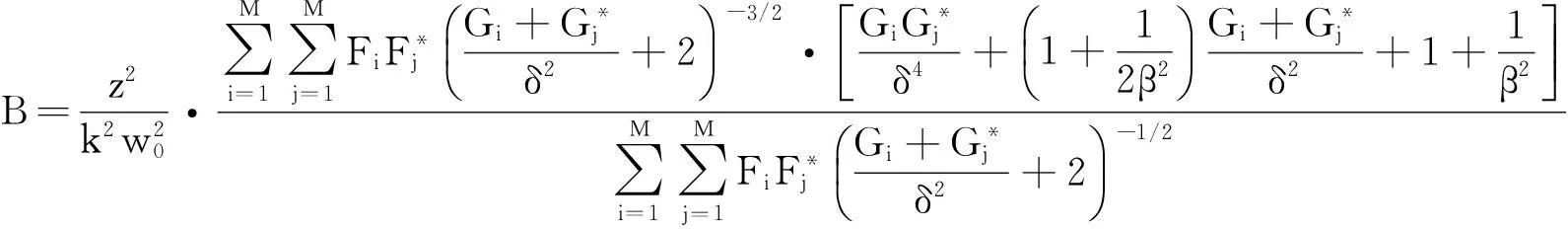
(8)
其中,β=σ0/w0为相干参数,δ=d/w0。
在自由空间中,瑞利区间zR|free定义为光束横截面积扩展到源场处两倍时光束所传输的距离[13],那么由(6)式可得

(9)
求解上式后得到截断光束在自由空间中传输的瑞利区间为
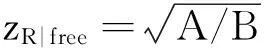
(10)
另一方面,截断光束在湍流中的二阶矩宽度可表达为[12]
w2(z)=A+B·z2+F·z3,
(11)
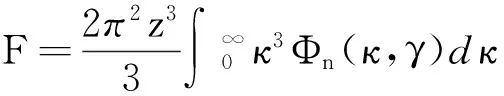
(12)
Φn(κ,γ)表示大气湍流的折射率起伏空间功率谱。
湍流的非Kolmogorov统计现已得到普遍认可,其中Φn(κ,γ)表示为[14]
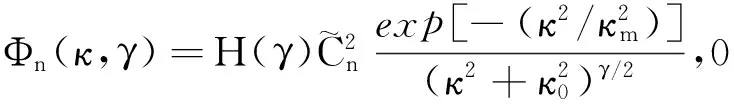
(13)

湍流中的瑞利区间定义为湍流中光束横截面积扩展至源场处两倍的传输距离,利用(11)式可知,

(14)
求解(14)式可得光束通过湍流传输的瑞利区间
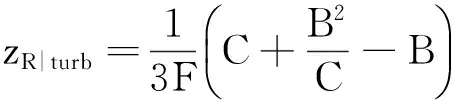
(15)
其中
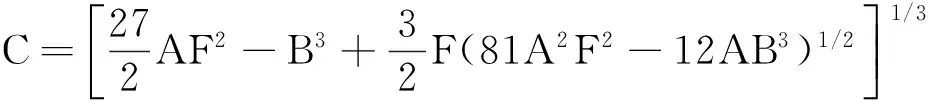
(16)

2数值计算与分析
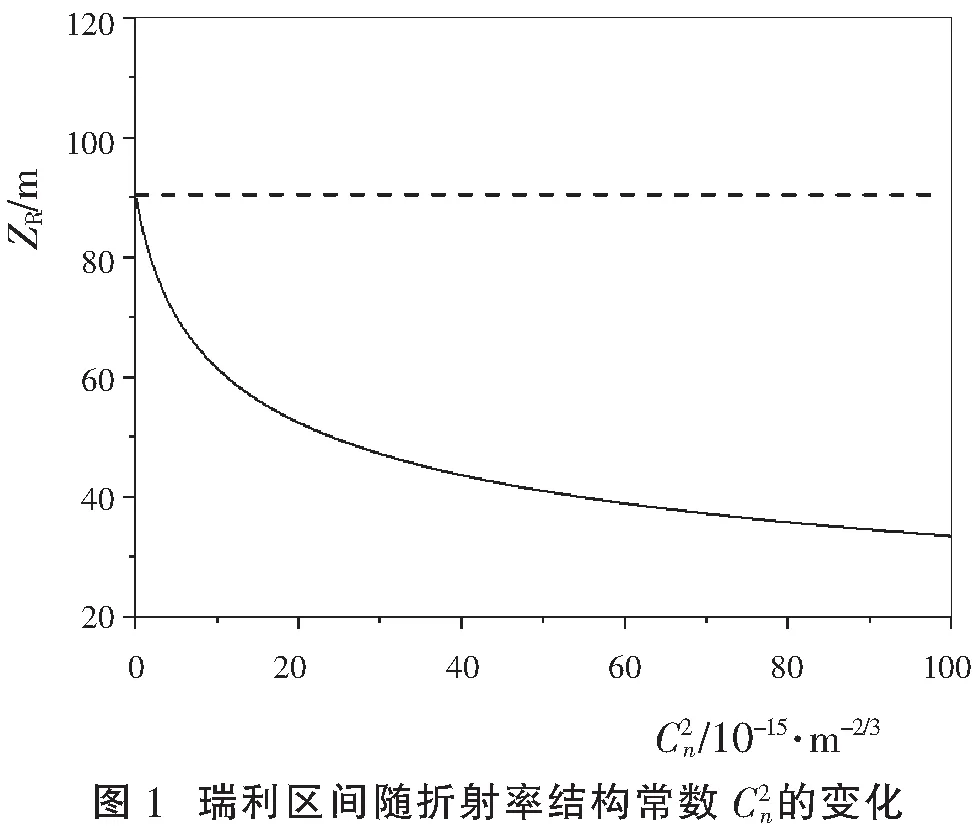



3结论

参考文献:
[1]ANDREWS L C,PHILLIPS R L.Lazer beam propagation through random media [M].Washington:SPIE Press,1998.
[2]WU G,GUO H,YU S,et al.Spreading and direction of Gaussian-Shell model beam through a non-Kolmogorov turbulence[J].Opt.Lett.,2010,35(5):715-717.
[3]黄永平,曾安平.厄米—高斯光束在非Kolmogorov大气湍流中的传输特性[J]. 光子学报,2012, 41(7): 818-823.
[4]陈晓文,李宾中,汤明玥.部分相干厄米高斯光束的湍流距离[J].西华师范大学学报(自然科学版),2014,35(1):82-86.
[5]XU H F,CUI Z F,QU J.Propagation of elegant Laguerre-Gaussian beam in non-Kolmogorov turbulence[J].Optics Express,2011,19(22):21163-21173.
[6]SIEGMAN A E.Lasers[M].Mill Valley,CA:University Science Books,1986.
[7]JI X L.Rayleigh range of Hermite-Gaussian array beams[J].Chin.Phys.Lett.2009,26(12):124210.
[8]JI X L,PU Z C.Effects of atmospheric turbulence on the polarization of apertured electromagnetic Gaussian Schell-model beams [J].J.Opt.A:Pure Appl.Opt.,2009,11(4):045701.
[9]陈晓文,李宾中,汤明玥.受光阑限制的部分相干光通过湍流大气传输的方向性[J].中国激光,2012,39(9):0913002.
[10]CHU X X,NI Y Z ,ZHOU G Q.Propagation analysis of flattened circular Gaussian beams with a circular aperture in turbulenct atmosphere[J].Opt.Commun.,2007,274(1):274-280.
[11]WANG S C H,PLONUS M A.Optical beam propagation for a partially coherent source in the turbulent atmosphere[J].Journal of the Optical Society of America A,1979,69(9):1297-1304.
[12]GBUR G,WOLF E.Spreading of partially coherent beams in random media [J].Journal of the Optical Society of America A,2002,19(8):1592-1598.
[13]汤明玥,李宾中,王宇峰,等.非Kolmogorov湍流对高斯—谢尔光束的瑞利区间和湍流距离的影响[J].中国激光,2014,41(10):1013002.
[14]邓金平,季小玲,陆璐.多色部分相干偏心光束在non-Kolmogorov湍流中的传输[J].物理学报,2013,62(14):144211.
Influence of Turbulence on the Rayleigh Range of Truncated Beams
WANG Yufeng1,CHEN Xiaowen1,TANG Mingyue2
(1.Imaging Department,North Sichuan Medical College,Nanchong Sichuan 637000,China;2.Department of Basic Medicine,North Sichuan Medical College,Nanchong Sichuan 637000,China)
Abstract:Using the extended Huygens-Fresnel principle and integral transform technique,the expressions for the Rayleigh range of truncated beams propagating through free space and turbulence are derived,and the influence of the beam parameters and turbulence parameters on the Rayleigh range is studied.It finds that Rayleigh range in turbulence decreases with increasing intensity of turbulence.On the other hand,Rayleigh range increases with increasing coherence parameter and truncation parameter,either in free space or turbulence.When the value of or is small,the influence of turbulence on the Rayleigh range can be omitted;but the influence of turbulence on the Rayleigh range increases with increasing of and .
Keywords:truncated beams;Rayleigh range;turbulence;truncation parameter
文章编号:1673-5072(2016)02-0214-04
收稿日期:2015-06-12
基金项目:四川省教育厅资助项目(12ZB048、13ZB0244)
作者简介:王宇峰(1969—),男,四川南充人,讲师,主要从事激光传输与控制研究。 通讯作者:陈晓文(1984—),男,江西景德镇人,讲师,主要从事激光传输与控制研究。E-mail:56833804@qq.com
中图分类号:O436.3;TN012
文献标识码:A
DOI:10.16246/j.issn.1673-5072.2016.02.018
