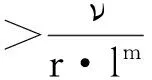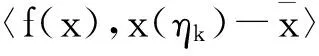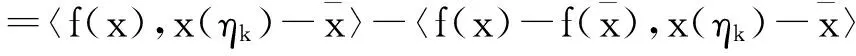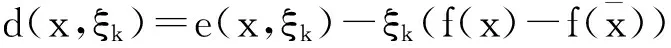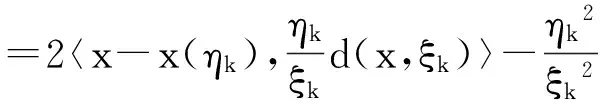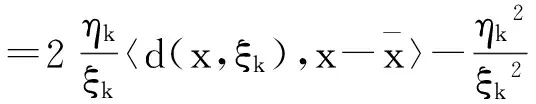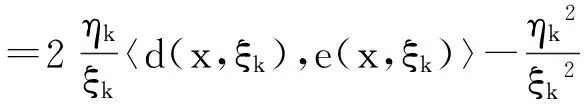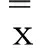伪单调变分不等式的次梯度外梯度投影算法
2016-07-07李涵,杨丽,李军
李 涵,杨 丽,李 军
(西华师范大学 数学与信息学院,四川 南充 637009)
伪单调变分不等式的次梯度外梯度投影算法
李涵,杨丽,李军
(西华师范大学 数学与信息学院,四川 南充637009)
摘要:在有限维欧式空间中研究了Censor,Gibali和Reich意义下变分不等式的次梯度外梯度投影算法。在伪单调假设条件下,利用He和Liao所提出的线搜索条件,证明了由次梯度外梯度投影算法所产生的迭代序列强收敛到经典变分不等式的解。去掉了Censor,Gibali和Reich文章中关于变分不等式所涉及映像的Lipschitz连续性条件。
关键词:变分不等式;次梯度外梯度投影算法;线搜索;伪单调
0引言
变分不等式的模型VI(S,f)是指: 寻找x*∈S, 使得
f(x*),y-x*≥0,∀y∈S,
(1)
其中S⊂Rn是非空闭凸集,f∶Rn→Rn为一个单值映射。用SOL(S,f)表示变分不等式VI(S,f)解集。变分不等式问题是优化理论中一个十分重要的问题,其在经济、金融和管理, 交通运输和博弈论等大量问题中都有广泛的应用。取x∈Rn, 称πS(x)∶=arg min{‖x-z‖∶z∈S}为x在S上的投影。最简单的解决VI(S,f)问题的投影算法[1]:取x0∈Rn,序列{xk}由下面的法则产生
xk+1=πS(xk-τ·f(xk))。
在变分不等式的投影算法中,Goldstein-Levitin-Polyak投影算法[2],邻近点算法[3]以及Korpelevich外梯度算法[4]都是比较经典的投影算法。其中,Facchinei和Pang[5]为了得到下一个迭代点xk+1,其算法通过两次投影。具体如下:给出一个迭代点xk,计算
yk=πS(xk-τ·f(xk)),
(2)
xk+1=πS(xk-τ·f(yk)),
(3)
其在优化中的应用十分广泛[6]。与此同时,许多学者也在这方面作了更深层次的研究。Iiduka用xk和yk的组合去替换(3)式
xk+1=πS(αkxk+(1-αk)yk),
Tk∶={w∈Rn∶〈(xk-τ·f(xk))-yk,w-yk〉≤0},
将(3)式中的非空闭凸集S变为半空间Tk,即
xk+1=πTK(xk-τ·f(yk)) 。
Censor,Gibali和Reich将外梯度投影算法的固定投影集合变动, 他们证明当函数f满足伪单调以及Lipschitz连续条件时, 由(2),(3)产生的序列{xk},{yk}, 满足下式:
‖xk+1-x*‖2≤‖xk-x*‖2-(1-τ2L2)‖yk-xk‖2,∀k≥0,
这里τ>0,Lipschitz常数L>0。从而在解集非空的假设下证明了该迭代算法收敛到VI(S,f)的解。
本文在此基础上,结合Korpelevich和He的外梯度算法,借助于线搜索技巧,并灵活地运用Censor,Gibali和Reich构造的投影平面性质,在f满足伪单调的前提下,将函数f的Lipschitz连续性条件降低到连续性条件,并证明其收敛性。
1预备知识
首先我们回顾一些相关的概念和结论。
定义1令C⊂Rn是非空集合,f∶Rn→Rn是连续映射,称f在C上是伪单调的, 若∀x,y∈C,
〈f(x),y-x〉≥0⟹〈(f(y),y-x〉≥0。
引理1[9]如下结论成立:x∈SOL(S,f)⟺‖x-πS(tf(x))‖=0,∀t>0。
记et(x)=x-πS(x-tf(x)),则有
0 引理2[10]P为任意非空闭凸集,x,y是欧式空间中的任意两点, 对于投影算子πP(x),πP(y),则有下式成立 ‖x-u‖2≥‖x-πP(x)‖2+‖u-πP(x)‖2,∀u∈P; ‖πP(x)-πP(y)‖≤‖x-y‖。 2算法及收敛性 算法1(ⅰ)取定参数,ν∈(0,1),l∈(0,1),r>0及初始点x0∈Rn,令k=0。 (ⅱ)对当前迭代点xk, 计算ξk∶=r·lmk,yk=πS(xk-ξkf(xk))。 其中mk为使得下式成立的最小正整数m r·lm‖f(xk)-f(πS(xk-r·lmf(xk)))‖≤ν‖xk-πS(xk-r·lmf(xk))‖ 。 如果xk=yk,则停止;否则令 Tk∶={u∈Rn∶(xk-ξkf(xk))-yk,u-yk≤0}, (4) 计算 xk+1=πTk(xk-ηkf(yk)) , (5) (ⅲ)令k=k+1,回到(ⅱ)。 引理3[11]假设f连续, 则存在最小正整数m使得下式成立 r·lm‖f(xk)-f(πS(xk-r·lmf(xk)))‖≤ν‖xk-πS(xk-r·lmf(xk))‖ 。 (6) 证明假设(6)不能在有限步内实现, 则对于∀m∈Z+,有 (7) 对于(7)的左端, 当m→∞时,有r·lm→0。从而,xk-r·lmf(xk)→xk, 则(7)式的左端趋近于‖f(xk)-f(πS(xk))‖。以下分两种情况讨论: ①若xk∈S,有f(πS(xk))=f(xk),于是根据f和πS的连续性可得当m→∞时, ‖f(xk)-f(πS(xk-r·lmf(xk)))‖→0。 (8) ②若xk∉S, (7)式变形为 r·lm‖f(xk)-f(πS(xk-r·lmf(xk)))‖>ν‖xk-πS(xk-r·lmf(xk))‖ , 当m→∞时,r·lm→0,则r·lm‖f(xk)-f(πS(xk))‖→0。右端趋近于ν‖xk-πS(xk)‖,由于ν‖xk-πS(xk)‖>0,矛盾。 综上,结论得证。 此引理表明线搜索是可行的。 (9) 证明由x*∈SOL(S,f),且S⊆Tk(详见文献[8]),所以x*∈Tk。 再结合引理2及(5)式可得 ‖xk-ηkf(yk)-x*‖2≥‖xk+1-x*‖2+‖xk-ηkf(yk)-xk+1‖2 ‖xk+1-x*‖2≤‖xk-ηkf(yk)-x*‖2-‖xk-ηkf(yk)-xk+1‖2 =‖xk-x*‖2-2xk-x*,ηkf(yk)+ηk2‖f(yk)‖2- =‖xk-x*‖2-2xk-x*,ηkf(yk)-‖xk-xk+1‖2+2〈xk-xk+1,ηkf(yk)〉 =‖xk-x*‖2-‖xk-xk+1‖2-2〈xk+1-x*,ηkf(yk)〉。 (10) 取ø(ηk)=‖xk-x*‖2-‖xk+1-x*‖2,并结合(10)式得 ø(ηk)≥‖xk-xk+1‖2+2ηk〈xk+1-x*,f(yk)〉, (11) 其中〈f(yk),xk+1-x*〉=〈f(yk),yk-x*+xk+1-yk〉 =〈f(yk),yk-x*〉+〈f(yk),xk+1-yk〉 。 因为x*∈SOL(S,f),所以〈f(x*),yk-x*〉≥0。由于f在S上伪单调, 并结合定义1得 〈f(yk),yk-x*〉≥0 。 所以(11)式进一步化为ø(ηk)≥‖xk-xk+1‖2+2ηk〈f(yk),xk+1-yk〉。 (12) (13) 结合(13)式得 (14) 令 (15) 将(15)代入(14)式进一步化为下式 (16) (17) 将(16),(17)代入(12) (18) =2τ(x,ξk)·〈e(x,ξk),d(x,ξk)〉-τ(x,ξk)·〈e(x,ξk),d(x,ξk)〉 =τ(x,ξk)·〈e(x,ξk),d(x,ξk)〉。 (19) ‖xk-x*‖→α, (20) 所以‖xk-x*‖2-‖xk+1-x*‖2→0。 再结合(9)可得 从而 ‖xk-yk‖→0, (21) 即 ‖e(xk,ξk)‖→0。 (22) ①若inf{ξk}=ξ>0,又因为ξki≥ξ,并由引理1知‖e(xki,ξki)‖≥‖e(xki,ξ)‖≥0。 所以 ②若inf{ξk}=ξ=0,不失一般性,可设子列ξki→ξ=0(i→∞)。 结合(6)式知 所以对充分大的j有 ‖f(xkij)-f(πS(xkij-ξkijl-1f(xkij)))‖>ν‖e(xkij,1)‖。 (23) 又因为 ‖xkij-πS(xkij-ξkijl-1f(xkij))‖≤‖xkij-πS(xkij-ξkijf(xkij))‖+ ‖πS(xkij-ξkijf(xkij))-πS(xkij-ξkijl-1f(xkij))‖, (24) 由引理2知 ‖πS(xkij-ξkijf(xkij))-πS(xkij-ξkijl-1f(xkij))‖≤ξkij|1-l-1|‖f(xkij)‖, 结合(24)可得 ‖xkij-πS(xkij-ξkijl-1f(xkij))‖≤‖xkij-ykij‖+ξkij|1-l-1|‖f(xkij)‖。 再结合(21)知 ‖xkij-ykij‖→0。 致谢非常感谢审稿人和叶明露博士对本文提出了许多宝贵的修改意见和建议,这些中肯的意见和建议大大改进了本文的初稿。 参考文献: [1]SIBONY M.Methodes iterative pour les equations et inequations aux derivees partiells non lineares de type monotone[J].Calcolo(French).1970,7(1):65-183. [2]GOLDSTEIN A A.Convex programming in Hilbert space[J].Bulletin of the American Mathematical Society.1964,70(5):709-710. [3]ROCKAFELLAR R T.Augmented lagrangians and applications of the proximal point algorithm in convex programming[J].Mathematics of Operations Research.1976,23(1):97-116. [4]KORPELEVIC G M.An extragradient method for finding saddle points and other problems[J].Ekonom.i Mat.Metody (Russian).1976,12(4):747-756. [5]FACCHINI F,Pang J S.Finite-dimensional variational inequalities and complementarity problems[M].Vols I and II,Springer-Verlag,New York,NY,USA.2003. [6]KINDERLEHRER D,STAMPACCHIA G.An introduction to variational inequalities and their applications[M].Academic Press.1980. [7]NOOR M A.Some development in general variational inequalities[J].Applied Mathematics and Computation.2004,152(2):199-277. [8]CENSOR Y,GIBALI A,REICH S.Extensions of korpelevich’s extragradient method for the variational inequality problem in Euclidean space[J].Optimization.2012,61(9):1119-1132. [9]HAN Q M,HE B S.A predict-correct projection method for montone variant variational inqualities[J].Chinese Science Bulletin 1998,43(15):1264-1267. [10]HE B S,LIAO L Z.Improvement of some projection method for monotone nolinear variational inequalities[J].Journal Of Optimization Theory And Applications.2002,112(1):111-128. [11]HAN D R,HONG K L.Two new self-adaptive projection methods for variational inequality problems[J].Computers and Mathematics with Applications.2002,43(12):1529-1537. A Subgradient Exgradient Projection Method for Pseudomonotone Variational Inequalities LI Han,YANG Li,LI Jun (College of Mathematics and Information,China West Normal University,Nanchong Sichuan 637009,China) Abstract:In this paper,we investigate a subgradient exgradient projection method for variational inequalities in the sense of Censor,Gibali and Reich in finite dimensional spaces.Under pseudomonotonicity assumptions,by using the linear search condition of He and Liao we prove the convergence of this subgradient exgradient projection method.Compared with the assumptions by Censor,Gibali and Reich, we remove the Lipschitz continuity condition. Keywords:variational inequality;subgradient exgradient projection method;line search;pseudomonotonicity 文章编号:1673-5072(2016)02-0189-06 收稿日期:2015-07-06 基金项目:国家自然科学基金(11371015); 教育部科学技术重点项目(211163); 四川省青年科技基金(2012JQ0035) 作者简介:李涵(1991—) ,女,四川南充人, 硕士研究生, 主要从事优化理论及应用研究。 通讯作者:李军(1974—) ,男,四川旺苍人, 博士,教授,主要从事优化理论及应用研究。E-mail:junli1026@163.com 中图分类号:O221 文献标志码:A DOI:10.16246/j.issn.1673-5072.2016.02.012